乘法逆元
就是
此时b就是a模p意义下的逆元,即
下面我们用inv[a]表示a模p意义下的逆元。
逆元是好东西啊
有时候我们需要算出 a/b mod p 的值,用朴素的方法,我们只能在 a 上不断加 p ,直到它能被 b 整除为止。
当 a,b,p 都很大的时候,这种方法就只能凉凉了,但如果有了逆元,我们就可以非常方便,快捷地求解。
——————某位大佬的话所以我先讲讲逆元性质:
唯一性就不用讲了
1.积性
假如a与b互质,
2.乘变除
证明如下:
两边都乘一个 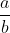 ,就得到了上面的式子
,就得到了上面的式子
至于逆元的求法,有很多,我只讲四种。
首先,是求单个逆元
1.费马小定理
当 p 为素数时:
所以
所以 就是a在模p意义下的逆元,快速幂求出








 本文详细介绍了乘法逆元的概念,包括积性和乘变除性质,并讲解了如何使用费马小定理和扩展欧几里得算法求单个逆元。接着探讨了欧拉函数筛法和线性递推在求多个逆元中的应用。同时,文章通过两道洛谷题目实例展示了逆元在解决实际问题中的应用,并提醒读者在递归函数中慎用内联函数以优化性能。
本文详细介绍了乘法逆元的概念,包括积性和乘变除性质,并讲解了如何使用费马小定理和扩展欧几里得算法求单个逆元。接着探讨了欧拉函数筛法和线性递推在求多个逆元中的应用。同时,文章通过两道洛谷题目实例展示了逆元在解决实际问题中的应用,并提醒读者在递归函数中慎用内联函数以优化性能。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3415
3415

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








