【coq】函数语言设计 笔记 05 -tactics

参考博客：https://www.cnblogs.com/TheFutureIsNow/p/11963233.html

More Basic Tactics (Tactics)
• The apply Tactic
• The apply with Tactic
• The injection and discriminate Tactics
• Using Tactics on Hypotheses
• Varying the Induction Hypothesis
• Unfolding Definitions
• Using destruct on Compound Expressions

介绍几种更为复杂的证明策略:

[apply]策略

• the goal to be proved is exactly the same as some hypothesis in the context or some previously proved lemma. （目标和 假设相同）
• 要使用[apply]策略，所应用的事实(结论)必须与目标完全匹配—例如，如果等式的左右两边交换，apply将不起作用，这个时候就需要使用关键字[symmetry]将等式的两边进行交换

在进行证明的时候经常遇到这样的情况，即要证明的目标与上下文中的某个假设或某个先前已证明的引理完全相同。
有时候可以使用[rewrite]然后在使用[reflexivity]来完成证明，如：

但也可以使用[apply]策略一步完成证明：

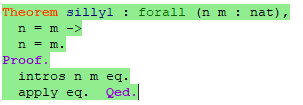
hypothesis n=m
goal n=m 二者相同

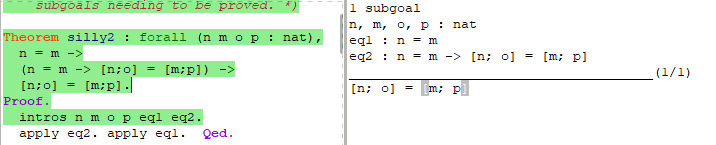
[apply]策略也适用于条件假设和引理:
apply用于化解 蕴含
举例

eq n = m -> [n; o] = [m; p]
goal [n; o] = [m; p]

apply eq后

goal n=m

连环蕴含

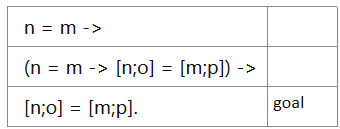
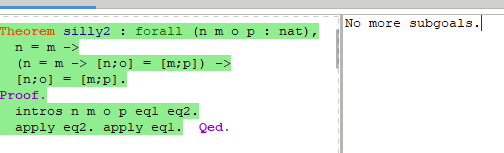
通常，当我们使用**[apply H]时，而语句H是以关键字forall开始的，也就是说语句H绑定了一些通用的变量。当Coq根据H的结论匹配当前目标时，它将尝试为这些变量找到合适的值。例如，在上面的例子中使用语句[apply eq2]时，eq2中的通用变量q用n实例化，r用m实例化**。

需要注意的一点是，要使用[apply]策略，所应用的事实(结论)必须与目标完全匹配—例如，如果等式的左右两边交换，apply将不起作用，这个时候就需要使用关键字**[symmetry]将等式的两边进行交换：

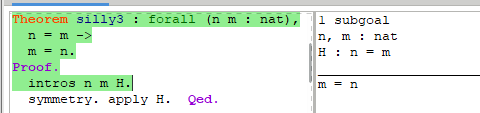
[apply with]策略

[apply with]和[apply]其实没有太大区别，只不过[apply with]允许指定用上下文中的变量代替引用的假设或者结论中的绑定变量。
先看一个例子：
证明方法1 - rewrite

证明方法2 -apply with

直接使用apply 无法寻找到变量

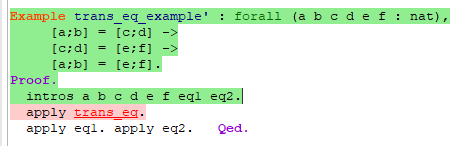
使用apply with

apply可以告诉（通过匹配目标和结论），它应该用[nat]来实例化X，用[a,b]来实例化n，用[e,f]来实例化o。然而，这个匹配过程并不能确定m的实例化

我们必须通过在apply的调用中加入 "with (m:=[c,d]) "来明确地提供一个实例。apply with可以指定上下文中的变量作为重写的参数。
实际上，with子句中的名称m不是必需的，因为Coq通常足够聪明，能够弄清楚我们正在实例化哪个变量。我们可以简单地写成apply trans_eq with [c;d]。

证明方法3 -transitivity

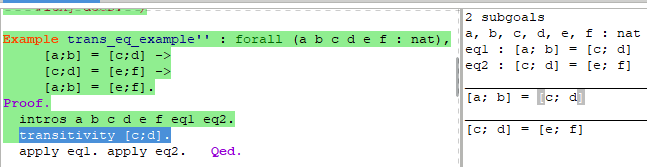
[injection]和[discriminate]策略

回顾之前定义自然数的语句：

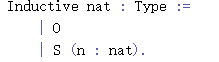
从定义的语句中很明显能够看出，每个自然数都只能是两种情况中的一种：要么是是由构造器O构成的，要么是由构造器S中构成的。这也是基础证明策略[destruct]和[induction]的基本原理。
然而还能够从自然数的定义语句中看出两外两点：这两条规则可以适用于任何一个递归定义的变量类型。

这个定理也可以使用[injection]策略进行证明：

injection
injection H as 新的H们（由H推导出的内容）

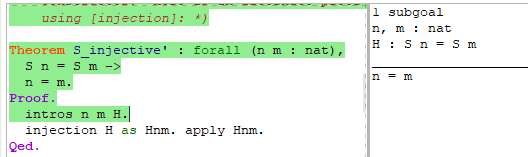
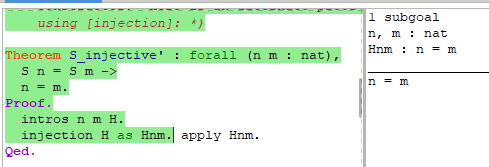
通过[injection H]语句，Coq会生成它可以依据构造函数的单射性推导出的所有方程。每一个这样的方程都是作为目标的前提加入的，而在这个例子中，添加了前提n=m。而这些前提也会成为后续证明的子目标。
此外，还可以使用关键字as引入一个变量来绑定这些前提，如：

不相交原则是指两个变量以不同的构造函数(如[O]和[S]，或[true]和[false])永远不可能相等。这意味着，任何时候我们发现上下文中某个假设断言两个不同构造器的变量相等，那么就可以得到任何想要的结论，因为假设是不成立的。
即 由 非、不可能成立的东西 推出 all
[discriminate]策略具体化了这个原则，通常这个策略被用在某个断言两个不同构造器构造的变量相等的假设上，然后使用这个策略快速完成当前的目标。例如：

可以将[discriminate]策略理解为：如果证明过程中某个荒谬的假设成立，那么推出的任何结论也是成立的，如：

此时蕴含语句，需要intro 引入H 和goal

H中存在E,H 其中H未谬论，所以可推导出任何结论

[unfold]

有时在证明过程中需要手动展开一个已经被一个[Definition]所定义好的函数名称，以便更好操纵等式的右边。
例如，定义一个平方函数：

Definition square n := n * n.

然后基于这个定义进行以下证明：

Theorem square_mult : forall n m, square (n * m) = square n * square m.
Proof.
intros n m. (*Did nothing*)unfold square.
rewrite mult_assoc.
assert (H : n * m * n = n * n * m). {rewrite mult_comm. apply mult_assoc. }rewrite H. rewrite mult_assoc. reflexivity.
Qed.