强化学习第六章：随机近似与随机梯度下降_rm算法为什么可以在不清楚表达式的情况下求解-CSDN博客

本文链接：https://blog.csdn.net/qq_42828479/article/details/139298199

强化学习第六章：随机近似与随机梯度下降

随机近似算法(Stochastic Approximation, SA)
RM算法(Robbins-Monro, RM)
RM算法与蒙特卡洛方法
随机梯度下降算法
总结
参考资料

随机近似算法(Stochastic Approximation, SA)

SA算法是一类寻根（方程求解）或优化问题的 随机迭代 算法。随机采样，迭代近似。还有，SA相较于其他方法（比如梯度下降）的强大之处在于 不需要知道 目标函数或者其导数或梯度的 表达式 。

RM算法(Robbins-Monro, RM)

RM算法是SA算法中非常经典的一个算法。

RM算法干什么的

假使，现在求解的问题：
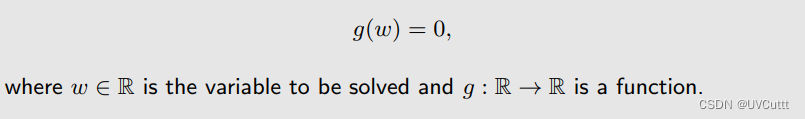
在这里插入图片描述
其他类似的问题（优化问题等）也可以转化为方程求根问题：

MakaBaka表示很熟悉，不就是求方程的根 w 嘛，但是挠了挠头发现连方程都不知道是啥，咋求根呢？MakaBaka手指一掐，白眼一翻，喃喃道：“RM算法助我！！！”。

RM算法怎么干的

下面这么干的：
在这里插入图片描述
MakaBaka拿着 wk 发现拿到的 g(w) 不够好，该如何优化呢，RM告诉MakaBaka说执行一个仪式：“把 wk 往下面的黑盒里面塞，得到 g(w) 之后加噪音拿到 g˜(wk, ηk) ，用 wk 减去 g˜(wk, ηk) 的一部分，这部分是多少呢，由 ak 决定”。
在这里插入图片描述
这样得到的 wk+1 就比 wk 更好吗？举个直观的例子验证一下，现在有这么一个问题：

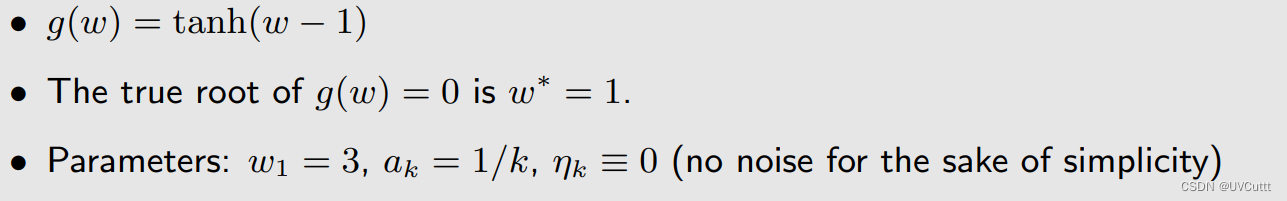
根据RM的仪式得到的中间过程：

分析一下：

MakaBaka笑着说：“每次 wk 减去 ak*g˜(wk, ηk) 之后都能朝着根前进，随着 k 增大， g(w) 逐渐收敛到0， g˜(wk, ηk) 中噪音的噪音越来越大， ak 逐渐收敛到0，太神奇了”。

RM算法为什么能这么干

细心和眼尖的人已经发现了，上面举的例子是不是个巧合呢，其他的行不行，比如单调递减的呢？好问题，这里给出什么时候能向上面那样做，RM原话：
在这里插入图片描述
MakaBaka表示RM原话看不懂，说说人话：

条件一：梯度的限制
这个条件约束了函数的梯度，得 大于零 ，让函数单调递增， 有唯一解 。但是不能太大，太大冲破了天际永远也找不到回家了路了，MakaBaka想着。
条件二：系数ak的限制

为什么要这样限制呢，将RM算法变换一下：

所以需要当k趋近无穷的时候ak趋近于0，让w收敛到真根：

OK，目的是： k趋近无穷的时候ak趋近于0 。如何限制？MakaBaka挠了挠头，看向了第二个限制：

巧了嘛，这不是，前者就完成了上面的目的，后者是干什么的？后者是让 ak慢慢减小到0 ，当k趋近无穷，ak趋近0，而不是说k等于某个常数num，ak就为0了，如果这样到达num步之后，后面就在做 无用功 (回想RM过程)了。后者的第二层作用是让w的初始值的选取可以是随心所欲的，不受真根的影响：

说的很清楚，假设 sigma(k=1,k=n)(ak)<无穷 ，那w的选取就被限制了，他离真实根的差是有界的，有界说明不能放飞自我地选。
条件三：噪音ηk的限制
引入中心为 g(w)=0* 的噪声，同时让噪声的方差有界，MakaBaka转了转自己的脑子，理解并得到了的两个猜想： 如果不约束均值，那么就引入了系统性误差，导致结果偏离真实根？ 如果不约束方差，假如噪声取了无穷，那么会让算法无法收敛？

RM算法与蒙特卡洛方法

上面提到的RM算法和之前学得蒙特卡洛方法有什么关系吗，为什么要学RM算法？
MakaBaka吧蒙特卡洛方法拿在手里揉了揉，拆了拆，发现了一件事，公式可以变个型：
在这里插入图片描述
恐怖如斯，之前近似期望的时候需要用N个样本来计算均值，现在给出了迭代的形式，那这里就有两种方式进行近似了：

Incremental形式再推广一下：

为啥要搞成这样呢，这这东西最终能让 w 收敛到期望吗，当 ak = 1/k 的时候就是蒙特卡洛，是收敛的吗？
在这里插入图片描述
对于ak方求和：

ln(n)是发散的，所以ak方求和也是发散的。
对于ak求和也有结论是收敛到一个常数的：

ak = 1/k 是蒙特卡洛近似，是收敛的。
上面的Incremental推广式和RM算法长得有点像，能不能说明上面的式子是个RM算法来间接证明呢？
MakaBaka发现了关键：假如 wk - xk = g˜(wk, ηk) ，那上面不就是一个RM算法了吗。为了达到这个目的，考虑下面这样一个 g(w) :
在这里插入图片描述
采个样就能得到：

MakaBaka拿出了尘封的草稿纸：

所以有：

目的达成，这就是一个RM算法。
最后，来段糕手看的证明：

随机梯度下降算法

前面也提到了很多梯度相关的东西，RM算法靠近真实根利用的是减去 ak*g˜(wk, ηk), 那这几种是怎么算的呢，哪些跟RM是一类的？
假设现在有一个优化问题：
在这里插入图片描述
这个优化过程为一步步执行，有下面三种方式。

梯度下降算法(Gradient Descent, GD)

利用函数的真实梯度来求解，这需要知道函数的样子(才能求出梯度)：
在这里插入图片描述

批量梯度下降算法(Batch Gradient Descent, BGD)

假设不知道函数长什么样子呢，也就说求不出梯度，那就用蒙特卡洛思想来近似梯度：
在这里插入图片描述
Batch指的就是n个样本。收集完了之后才能近似梯度的期望。

随机梯度下降算法(Stochastic Gradient Descent, SGD)

假如我随机采样一个样本作为梯度的期望呢：
在这里插入图片描述

随机梯度下降算法收敛性分析

随机选一个准不准啊。随机的不准，但梯度下降肯定是准的，从梯度下降过度到随机梯度下降分析下：
在这里插入图片描述
其中随机梯度与真实梯度之间存在一个误差：

接下来就是见证奇迹的时刻，开始套RM框架：

目的是找 g(w) = 0 的根：

没的说，小学生也会的加加又减减，顶级，MakaBaka拍了拍手。

条件一：函数的二阶导数
即Hessian矩阵，由二阶偏导数以及二阶混合偏导数组成，Hessian矩阵正定（每个值都大于零）表示函数是凸的。凸的就保证每次迭代的时候能 最快地向最小值 （凸函数的极小值即为最小值）靠近。同时又 不能太大 ，能让算法 稳定收敛 。
条件二：ak的约束
MakaBaka回忆了起来。
条件三：样本独立同分布
之前的RM算法 显式地对误差 的方差收敛性提出要求，因为它一般处理的是更为抽象的随机逼近问题，误差直接影响到逼近的准确性和收敛性。这里通过 假设样本i.i.d. ，确保在有限样本的情况下梯度估计的无偏性和方差控制，相当于简化了。

随机梯度下降算法收敛过程分析

分析下随机梯度下降算法收敛过程中当w越来越靠近w*的时候误差是怎么变化的。
用随机梯度与批量梯度之间的关系定义一个相对误差项：
在这里插入图片描述
加加又减减：

分式下方减个0不影响，同时这样利用中值定理（拉格朗日拉师傅的）获得了关键因子 (wk - w)，MakaBaka挠了挠头，死去的记忆开始攻击他，拉格朗日中值定理(Lagrange Mean Value Theorem, LMVT)：

又出现了二阶导数，那么函数是凸的，二阶导数是大于某个值的：

上面的式子，常数 (wk - w) 从期望计算拿出去，乘积绝对值等于绝对值乘积：
在这里插入图片描述
最终得到了这样一个相对误差的表达式：

这样就好分析了：