线性DP之背包问题

目录

1，0/1背包问题
2，完全背包问题
3，多重背包问题
4，混合三种背包问题
5，二维费用背包问题
6，分组背包问题
7，有依赖的背包问题
8，求背包问题的方案总数。
9，背包问题的究极分类！！！！！（特别重要也很特别）

1， 01背包问题

集合：f[i,j]考虑前i种物品占用容量为j的背包的最大价值
策略：对于任意容量下的背包，考虑当前的i物品只有放入或者不放入两种选择
原始状态转移：f[i][k]=max(f[i-1][k],f[i-1][k-space[i]]+w[i]);
抽出一次循环中的转移过程：（如图，只涉及i-1和i维）

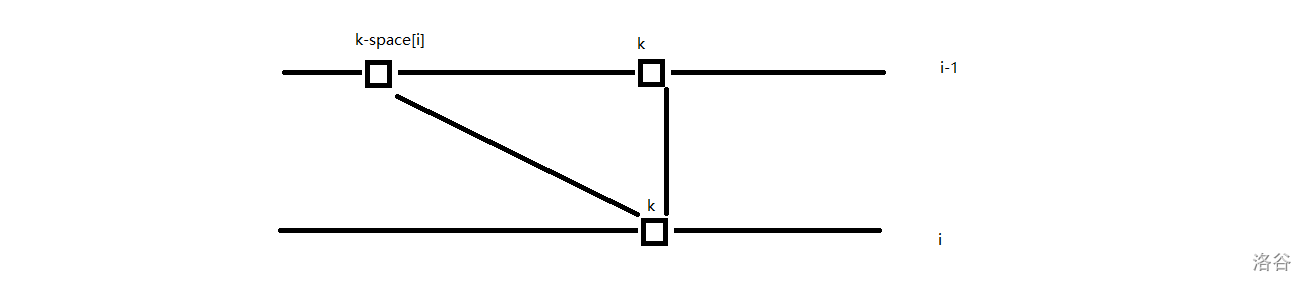
一维的背包其实就是两条线段的重合，由于循环顺序的特殊性，从最大的背包容量m迭代时，m-w[i]（可以假装它还是 i-1的时候的情况，因为这层循环压根没调用它）

以及由于线段重合造成循环的顺序只能从大到小，点的覆盖是其中关键所在

最终的代码：

int w[MAXN],f[MAXN],v[MAXN];

for(int i=1;i<=n;i++)        / /迭代枚举i个物品
	for(int k=m;k>=w[i];k--)/ / 迭代枚举背包容量  
		f[i]=max(f[k],f[k-w[i]]+v[i]);

2，完全背包问题

题面：同样的n件物品，对于每件想取多少就可以取多少
集合：f[i,j]考虑前i种物品占用容量为j的背包的最大价值
策略：对于任意容量下的背包，考虑当前的i物可以放几个
原始状态转移：f[i,j]=max(f[i-1,j], f[i-1][j-space[i]+w[i] , f[i-1][j-space[i]*2] + 2*w[i] ,...... f[i-1][j-space[i]*k] +k *w[i])
优化藏在数学规律里：

	f[i,j]=max(f[i-1,j], f[i-1][j-space[i]+w[i] , f[i-1][j-space[i]*2] + 2*w[i] , f[i-1][j-space[i]*3] +3 *w[i])  
	先写到3好了，足够说明问题
	
	f[i,j-space[i]]=max(f[i-1,j-space[i]], f[i-1][j-space[i]*2]+w[i] , f[i-1][j-space[i]*3] + 2*w[i])  
	
	 你很惊喜的发现 
	 f[i][j] 需要的：
	 f[i-1][j-space[i]+w[i] , f[i-1][j-space[i]*2] + 2*w[i] , f[i-1][j-space[i]*3] +3 *w[i] 的 max 不就是
	 f[i-1][j-space[i]]  （故意的分开！） +w[i] 吗？

优化的策略依稀有个影子了吧：就是把第三层循环涉及的对个数的枚举无限分割变小，直到只涉及两个，以后再用到就是无数个两个max判断的叠加了；

图片是在桌子上（jx记得把它绘出来啊！！）

最终的代码：

int space[MAXN];
int f[MAXN];
int v[MAXN];

for(int i=1;i<=m;i++)
	for(int k=w[i];k<=m;k++)
		f[i]=max(f[k],f[k-space[i]]+v[i]);  

3，多重背包问题

题面：同样的n件物品，对于每件只能取固定的s件
集合：f[i,j]考虑前i种物品占用容量为j的背包的最大价值
策略：
1，暴力转01，换个角度思考，其实一共就有n*s件物品可以备选，每件的价值和体积全部已知，01求解就好啦
2，二进制转01，倍增考虑，针对所有的整数，都是可以由2的n次方的无数个数组合出来的，但是这样可以大幅的缩减空间；
举个栗子 ：对于可能1000个数目备选的物品，转化为倍增处理的单个背包，只剩10个了

二进制拆包操作：

	for(int i=1;i<=n;i++)                迭代n次表示有n个物品
	{
		cin>>v>>w>>s;                    输入物品的相关数据
		for(int j=1;j<=s;j*=2)           倍增的产生用于合包的物品大小
		{
			s-=j;                        原包的大小一直浮动
			vec.push_back({v*j,w*j});    产生新的物品
		}
		if(s>0)vec.push_back({v*s,w*s});  处理倍增的小尾巴
	}

其余的就和01背包一样啦！
典例 AcWing5. 多重背包问题 II
AC 打卡代码

3，单调队列究极优化

4，混合的三种基础背包问题

策略：
1，由三种背包都可以滚动数组优化知，当前维度的物品是与前一个状态下的物品种类完全无关（无后效性得证！）
2，01背包是特殊的完全背包（在完全背包的大前提下可以顺便解决01）
典例AcWing 7. 混合背包问题
AC 打卡代码

5，二维费用背包问题

题面：有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。
思考：对于除多出的那一维的单维01，我们就是枚举物品并逆向迭代限制条件，现在的两维可以交换且互不影响，求解第i个物品的体积限制时，顺带也可解决重量限制
结论：只需加入新的一层逆向迭代求解新定义的限制即可

for(int i=1;i<=n;i++)
	{
		cin>>v>>h>>w;
		for(int j=mv;j>=v;j--)                        体积限制迭代  （mv为体积最大值）
			for(int k=mh;k>=h;k--)                    重量限制迭代  （mh为重量最大值）
				f[j][k]=max(f[j][k],f[j-v][k-h]+w);   正常转移即可
	}

典例AcWing 8. 二维费用的背包问题
AC 打卡代码

6，分组背包问题

题面：有n组物品，每组物品有若干个，同一组内的物品最多只能选一个。
策略：把01背包分组之后，只需在正常迭代的内部，加一次迭代，判断该组内能占用j空间的物品（这个前提很重要）中谁比较最优即可

	for(int i=1;i<=n;i++)
		for(int j=m;j>=0;j--)
			for(int k=1;k<=num[i];k++)         分组背包特性性的迭代，判断该组物品选谁最优
				if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);   

典例AcWing 9. 分组背包问题
AC 打卡代码

7，有依赖的背包问题

题面：
策略：

8，求背包问题的方案总计数以及打印

典例AcWing 9. 分组背包问题
AC 打卡代码

9，背包问题的究极分类！！！！！

就结果而言，分为：方案数，最小值和最大值问题
就转移过程而言，分为：至少型，恰好型，至多型

考虑结果，受到初始化的作用：

• 1，方案数的f[0]=1表示啥也不选也是一种方案
• 2，最大值的目的是在第一轮循环的时候借助max，巧妙的不用原数组的数据，那么考虑使用负无穷或0
• 3，最小值的目的和最大值一致，就是借助min性质，巧妙调开并覆盖元数组数据考虑使用正无穷

考虑转移，受到初始化和转移过程的作用：

恰好型

• 恰好的时候，f[0]=0 其余的无穷化，因为一个不选且占用空间恰好为0是合法的，其余的都是不合法解，不能用于转移
• 恰好类型的转移，负数空间不能转移，转移的下界就是0，这是实际意义决定的

至少型

• 至少类型的转移，f[0]=0 其余的无穷化，因为一个不选且占用空间至少为0是合法的，其余的都是不合法解，不能用于转移
• 至少类型的转移，负数空间可以转移，转移无下界，这是（至少）的实际意义决定的，由负数转移，说明选取这个物品会使某个数据大于需求值，这是符合至少的需要的

至多型

• 至多的时候，初始化所有的值为0，空间为0且选取0件物品的价值为0是合法的
• 其余的就视min还是max决定不合法情况的初始化是无穷大还是无穷小

Y总究极背包总结课，强推！！！！！！！

完结撒花！！！$\sqrt[{}^{{}^{400ACpj}}]{\frac{{}^{{ORZ}_{orz}^{OTZ}}}{{}_{{WA}_{QAQ}^{qwq}}}}$