【论文阅读】2024 ECCV Hierarchical Gaussian Mixture Normalizing Flow Modeling for Unified Anomaly Detectio-CSDN博客

本文链接：https://blog.csdn.net/qq_42854305/article/details/144041994

会议 2024 ECCV
paper https://www.ecva.net/papers/eccv_2024/papers_ECCV/papers/04634.pdf
Code https://github.com/xcyao00/HGAD

摘要

拆分摘要：
**定义：**统一异常检测（AD）是异常检测中最有价值的挑战之一，其中一个统一模型是用多个类别的正常样本训练的，目标是检测这些类别中的异常。
**背景：**对于这样一个具有挑战性的任务，流行的基于归一化流（NF）的AD方法可能会陷入“同质映射”问题，其中基于NF的AD模型倾向于为正常和异常特征生成相似的潜在表示，从而导致异常的高漏检率。
创新：在本文中，我们提出了一种新颖的层次高斯混合归一化流建模方法，用于完成统一异常检测，我们称之为HGAD。我们的HGAD由两个关键组件组成：类间高斯混合建模和类内混合类中心学习。与以前的基于NF的AD方法相比，层次高斯混合建模方法可以为归一化流的潜在空间带来更强的表示能力。通过这种方式，我们可以避免将不同类别的分布映射到同一个高斯先验中，从而有效地避免或减轻“同质映射”问题。我们进一步指出，不同类别中心的可区分性越大，越有利于避免偏差问题。因此，我们进一步提出了一种互信息最大化损失，以更好地构建潜在特征空间。我们在四个真实世界的AD基准测试中评估了我们的方法，我们可以显著提高以前的基于NF的AD方法，同时也超越了SOTA统一AD方法。代码将在以下网址提供：https://github.com/xcyao00/HGAD。
在这里插入图片描述

1 引言

异常检测在不同场景中受到了越来越广泛的关注和应用，例如工业缺陷检测 [4, 10, 20, 32, 35, 36]、视频监控 [1, 26]、医学病变检测 [28, 39] 和道路异常检测 [7, 30]。考虑到异常的高度稀缺性和正常类别的多样性，大多数先前的 AD 研究主要致力于无监督的单类学习，即仅利用单类正常样本学习一个特定的 AD 模型，然后检测该类中的异常。然而，这种一对一的范式在对许多产品类别进行训练和测试时需要更多的人力、时间和计算成本，并且当一个正常类别具有较大的类内多样性时表现不佳。
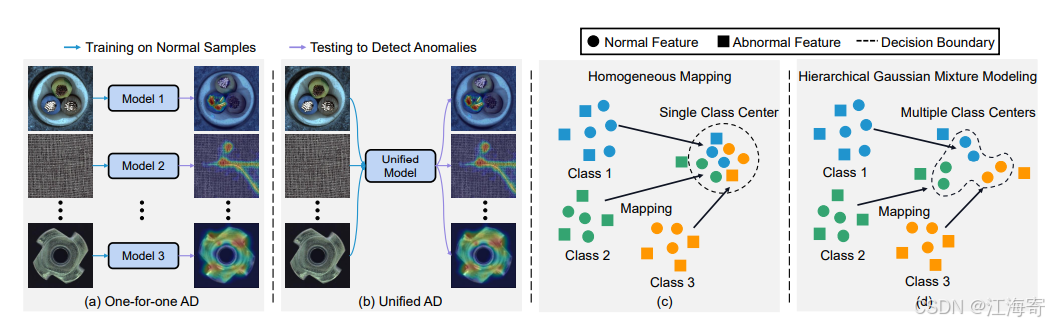
在这里插入图片描述

图 1：异常检测任务设置。我们的目标是实现一个统一的 AD 模型（b）。（c）将所有输入特征映射到相同的潜在类中心可能会引发 “同态映射” 问题。（d）我们提出了一种分层高斯混合建模方法，以更有效地捕获复杂的多类分布。
notes
这个图展示了两种不同的数据映射和聚类方法：同态映射（Homogeneous Mapping）和层次高斯混合模型（Hierarchical Gaussian Mixture Modeling）。

同态映射（Homogeneous Mapping）
在图的左侧（标记为c），同态映射是一种将不同类别的数据映射到一个共同的特征空间的方法。这种方法假设所有类别的数据都可以通过一个单一的中心点（Single Class Center）来描述。具体来说：

Class 1：蓝色方块，映射到一个共同的中心点。
Class 2：绿色方块，同样映射到这个共同的中心点。
Class 3：橙色方块，也映射到这个共同的中心点。
在同态映射中，所有类别的数据都被映射到同一个中心点，这意味着模型试图找到一个统一的分布来描述所有类别的数据。这种方法可能在类别之间具有相似特征时效果较好，但如果类别之间差异较大，可能会导致信息丢失。

层次高斯混合模型（Hierarchical Gaussian Mixture Modeling）
在图的右侧（标记为d），层次高斯混合模型是一种更复杂的方法，它允许每个类别有自己的中心点（Multiple Class Centers），并且这些中心点可以进一步组织成层次结构。

Class 1：蓝色方块，有自己的中心点。
Class 2：绿色方块，有自己的中心点。
Class 3：橙色方块，也有自己的中心点。
在层次高斯混合模型中，每个类别的数据都被映射到各自的中心点，这些中心点可以更精确地描述每个类别的特征。此外，这些中心点还可以通过层次结构相互关联，允许模型捕捉类别之间的复杂关系。

理解这两种方法的关键在于：
同态映射：强调所有类别数据的统一性，可能适用于类别之间差异不大的情况。
层次高斯混合模型：允许每个类别有自己的特征表示，并且可以构建类别之间的层次关系，适用于类别差异较大或需要更精细区分的情况。

在这项工作中，我们旨在解决一个更实际的任务：统一异常检测。如图 1b 所示，一个统一的模型使用来自多个类别的正常样本进行训练，目标是在不进行任何微调的情况下检测所有这些类别的异常。尽管如此，解决这样的任务是相当具有挑战性的。目前，有两种基于重建的 AD 方法来解决具有挑战性的统一 AD 任务，UniAD [35] 和 PMAD [34]。但是基于重建的方法可能会陷入 “相同快捷方式重建” 的困境 [35]，在这种情况下，异常也可以被很好地重建，导致异常检测失败。UniAD 和 PMAD 试图掩盖相邻或可疑的异常以避免相同的重建。然而，由于异常的规模和形状各不相同，掩蔽机制无法完全避免重建过程中的异常信息泄漏，相同重建的风险仍然存在。为此，我们考虑从正常数据分布学习的角度设计统一的 AD 模型。优点是我们原则上不再面临异常信息泄漏的风险，因为我们的方法基于正常数据分布并从根本上避免了重建。
具体来说，我们使用归一化流（NF）来学习正常数据分布 [12]。
归一化流：nf用于学习正常数据的分布，通过一个可逆的额双射映射，将复杂的原始数据分布转化为简单的潜在分布（通常假设为高斯分布），从而可以方便的计算出数据的概率密度函数。在异常检测中，通常通过比较输入数据和正常数据的概率密度来判断数据是否异常

然而，我们发现基于 NF 的 AD 方法在应用于统一 AD 任务时表现不理想。它们通常会陷入 “同态映射” 问题（见第 3.2 节），其中基于 NF 的 AD 模型倾向于为正常和异常输入生成较大的对数似然值（见图 2b）。
4 类是指图像中对象的类别，对于工业 AD，它指的是工业产品类别，例如在图 1 中，电缆、地毯等。
用于统一异常检测的分层高斯混合建模 3
我们将这个问题解释为：基于 NF 的 AD 方法 [12,36] 采用单峰高斯先验来学习多类分布（多模态）。这可以看作是学习从异构空间到潜在同态空间的映射。为了很好地学习映射，网络可能会被促使产生偏差，专注于粗粒度的共同特征（例如局部像素相关性），并抑制不同类特征之间的细粒度可区分特征（例如语义内容）[14]。因此，网络将不同的类特征同态地映射到接近的潜在嵌入中。因此，即使是异常也可以获得较大的对数似然值并且变得不太可区分。

在这里插入图片描述

为了解决这个问题，我们首先通过经验证实，映射到多模态潜在分布对于防止模型学习偏差是有效的（见图 2c）。因此，我们提出了一种基于 NF 的 AD 网络的类间高斯混合建模方法，以更有效地捕获复杂的多类分布。其次，我们认为类间高斯混合建模只能确保特征被吸引到整个分布，但缺乏类间排斥力，仍然导致对不同类特征的判别能力较弱。这可能导致不同的类中心坍缩到同一个中心。为了进一步提高类间可区分性，我们提出了一个互信息最大化损失，以将类排斥特性引入模型，以便更好地构建潜在特征空间，其中类中心可以相互推开。第三，我们引入了一种类内混合类中心学习策略，该策略可以促使模型即使在一个类内也能学习到不同的正常模式。最后，我们形成了一种用于统一异常检测的分层高斯混合归一化流建模方法，我们称之为 HGAD。总之，我们做出了以下主要贡献：
我们提出了一种新颖的统一 AD 方法：HGAD，其中分层高斯混合建模方法可以为归一化流的潜在空间带来更强的表示能力，以完成统一 AD 任务。
我们具体提出了三个关键设计：类间高斯混合建模、互信息最大化损失和类内混合类中心学习策略。
在统一 AD 任务下，我们的方法可以显著提高之前一对一基于 NF 的 AD 方法（例如 CFLOW-AD）的统一 AD 性能，将 AUROC 从 89.0%/94.0% 提高到 98.4%/97.9%，并且也优于最先进的统一 AD 方法（例如 UniAD）。

2 相关工作

异常检测
1）基于重建的方法是最流行的 AD 方法。这些方法依赖于这样的假设，即由正常样本训练的模型在异常图像区域会失败。许多先前的工作试图训练自动编码器 [18, 37]、变分自动编码器 [16] 和生成对抗网络 [2, 25] 来重建输入图像。然而，这些方法面临着 “相同快捷方式” 问题 [35]。2）基于嵌入的方法最近通过使用 ImageNet 预训练网络作为特征提取器显示出更好的 AD 性能 [3,8]。PaDiM [9] 提取预训练特征来为正常样本建模多元高斯分布，然后利用马氏距离来测量异常分数。PatchCore [20] 在此基础上进行了扩展，利用局部聚合特征并引入贪婪核心集子采样来形成名义特征库。3）知识蒸馏假设在正常样本上训练以学习教师的学生只能回归正常特征，但在异常特征上失败 [5]。最近的工作主要集中在特征金字塔 [24,31]、反向蒸馏 [10] 和非对称蒸馏 [23]。4）统一 AD 方法试图训练一个统一的 AD 模型来完成多个类别的异常检测。UniAD [35]、PMAD [34] 和 OmniAL [41] 是这个新方向上的三种现有方法。UniAD 是一种基于变压器的重建模型，有三个改进，它可以通过解决 “相同快捷方式” 问题在统一情况下表现良好。PMAD 是一种基于 MAE 的补丁级重建模型，它可以在一个图像内学习上下文推理关系，而不是类依赖的重建模式。OmniAL 是一个具有异常合成、重建和定位改进的统一 CNN 框架。

异常检测中的 GMM
先前的方法，DAGMM [38] 和 PEDENet [40]，也使用 GMM 进行异常检测。然而，我们的方法与这些方法有以下显著不同：1）不同的任务。DAGMM 用于非图像数据，PEDENet 用于一对一的图像异常检测。虽然它们都使用 GMM，但将它们用于统一异常检测并非易事。然而，我们的方法可以在统一 AD 任务中取得优势。2）不同的方法。DAGMM 和 PEDENet 都预测成员资格，然后使用预测的成员资格和 GMM 建模公式直接计算混合成分权重以及每个混合成分的均值和方差。我们的方法基于可学习的类中心和类权重。我们的方法对于分层高斯混合建模更有益，而 DAGMM 和 PEDENet 中的方法很难实现这一点。
异常检测中的归一化流
在异常检测中，归一化流被用于学习正常数据分布 [12,15,21,33,36]，在训练期间最大化正常样本的对数似然值。Rudolph 等人 [21] 首先通过估计预训练特征的分布来使用 NF 进行异常检测。在 CFLOW-AD [12] 中，作者进一步在多尺度特征图上构建 NF 以实现异常定位。最近，全卷积归一化流 [22,36] 已被提出以提高异常检测的准确性和效率。在 BGAD [33] 中，作者提出了一种基于 NF 的 AD 模型来解决有监督的 AD 任务。在本文中，我们主要提出了一种新颖的基于 NF 的 AD 模型（HGAD），具有三个改进以实现更好的统一 AD 性能。

3 方法

3.1基于归一化流的异常检测的初步知识

在后续部分，大写字母表示随机变量（RVs）（例如， $X$ ），小写字母表示它们的实例（例如， $x$ ）。一个随机变量的概率密度函数写为 $p (X)$ ，一个实例的概率值写为 $p_{X}(x)$ 。

归一化流模型 $[11, 13]$ 能够通过一个具有 $p (Z)$ 密度的易处理的潜在基础分布以及一个双射可逆映射 $\varphi: X \in \mathbb{R}^{d} \to Z \in \mathbb{R}^{d}$ 来拟合任意分布 $p (X)$ 。

然后，根据变量替换公式 $[29]$ ，任何 $\in X$ 的对数似然可以被估计为：
$\log p_{\theta}(x)=\log p_{Z}\left(\varphi_{\theta}(x)\right)+\log \vert\det J\vert \quad(1)$
其中 $\theta$ 表示可学习的模型参数，我们使用 $p_{\theta}(x)$ 来表示通过模型 $\varphi_{\theta}$ 对特征 $x$ 所估计出的概率值。 $\nabla_{x} \varphi_{\theta}(x)$ 是双射变换 $\varphi_{\theta}(x)$ 和 $\varphi_{\theta}^{-1}(z))$ 的雅可比矩阵。

模型参数 $\theta$ 可以通过在训练分布 $p (X)$ 上最大化对数似然来进行优化。损失函数被定义为：
$\mathcal{L}_{m}=\mathbb{E}_{x \sim p(X)}\left[-\log p_{\theta}(x)\right] \quad(2)$

在异常检测中，为了简单起见，通常假设正常特征的潜在变量 $Z$ 服从 $\mathbb{I})$ 分布 $[21]$ 。通过在公式 $(1)$ 中用 $p_{Z}(z)=(2 \pi)^{-\frac{d}{2}} e^{-\frac{1}{2} z^{T} z}$ （其中 $\varphi_{\theta}(x)$ ）进行替换，公式 $(2)$ 中的损失函数可以被写成：
$\mathcal{L}_{m}=\mathbb{E}_{x \sim p(X)}\left[\frac{d}{2} \log (2 \pi)+\frac{1}{2} \varphi_{\theta}(x)^{T} \varphi_{\theta}(x)-\log \vert\det J\vert\right]$

在训练之后，输入特征的对数似然可以被训练好的归一化流模型精确地估计为：
$\log p_{\theta}(x)=-\frac{d}{2} \log (2 \pi)-\frac{1}{2} \varphi_{\theta}(x)^{T} \varphi_{\theta}(x)+\log \vert\det J\vert$

接下来，我们可以通过指数函数将对数似然转换为似然：
$p_{\theta}(x)=e^{\log p_{\theta}(x)}$

因为我们在公式 $(2)$ 中是对正常特征的对数似然进行最大化，所以估计的似然 $p_{\theta}(x)$ 可以直接表示正态性（一个更大的值意味着更正常）。

因此，我们可以通过 $p_{\theta}(x)$ $[33]$ 将似然转换为异常分数。

3.2重新审视基于归一化流的异常检测方法

在统一异常检测（AD）任务的情境下，我们遵循基于归一化流（NF）的异常检测范式[12, 21]，并且重现了FastFlow [36]的相关操作，以此来估计由预训练骨干网络所提取出来的特征的对数似然。

然后，我们会将所估计得到的对数似然转换为异常分数，并且每隔10个训练轮次（epochs）就对AUROC指标进行一次评估。
在这里插入图片描述

正如图2a所展示的那样，经过一段时间的训练之后，模型的性能出现了严重的下降情况，然而与此同时，损失值却持续变得极小。相应地，总体的对数似然值变得非常大。

我们将这种现象归结于“同态映射”问题，也就是归一化流有可能会将所有的输入映射到极为接近的潜在变量上，进而针对正常特征和异常特征都会呈现出较大的对数似然值，这样就导致无法有效地检测出异常情况。

这种推测通过图2b中的可视化结果得到了经验层面的验证（更多的相关结果可以在附录图1中查看），在图2b中可以看到，正常特征和异常特征的对数似然值呈现出了高度的重叠状态。

正如我们在第1节中所解释的那样，这种现象产生的原因可能是模型过度地抑制了正常特征和异常特征之间那些细粒度的、能够用于区分的特征。

	在正常情况下，为了使变量符合正态分布，通常可以采用以下一些方法：
	数据预处理
	标准化：对数据进行均值为 0，方差为 1 的标准化处理，这可以使数据的分布更加集中，接近正态分布的形状。
	归一化：将数据映射到特定的区间，例如 [0, 1] 或 [-1, 1]，这有助于消除数据的量纲差异，使数据分布更加规整。
	模型选择和设计
	选择合适的概率分布模型来拟合数据，例如高斯混合模型（GMM），它可以通过多个高斯分布的组合来更好地拟合复杂的数据分布。
	在模型训练过程中，使用合适的优化算法和损失函数，以引导模型学习到数据的真实分布。例如，通过最大化似然函数来估计模型参数，使得模型输出的概率分布尽可能接近真实数据的分布。
	增加数据量和多样性
	收集更多的数据可以提供更丰富的信息，有助于模型更好地学习数据的分布特征。
	对数据进行适当的变换或扩充，如旋转、翻转、添加噪声等，可以增加数据的多样性，使模型能够学习到更全面的特征分布。
	特征工程
	对原始数据进行特征提取和选择，去除冗余或不相关的特征，保留对数据分布有重要影响的特征。
	通过组合或变换现有特征，创建新的特征，以更好地描述数据的分布。

然而，正如图2c和2d所展示的那样，我们所采用的这种统一的基于NF的AD方法能够更加有效地避免正常特征和异常特征的对数似然值出现高度重叠的情况，这表明对数似然偏差问题在我们的方法中表现得相对较轻。这也促使我们展开如下的分析。

下面，我们将正常特征表示为 $x_{n} \in \mathbb{R}^{d}$ ，把异常特征表示为 $x_{a} \in \mathbb{R}^{d}$ ，其中 $d$ 表示通道维度。

我们使用一个简单的单耦合层归一化流模型来进行粗略的分析。在训练过程中，前向仿射耦合[11]的计算方式如下：
$x_{1}, x_{2} = split(x_{n}); z_{1} = x_{1}, z_{2} = x_{2} \odot exp(s(x_{1})) + t(x_{1}); z = cat(z_{1}, z_{2}) \quad(4)$
在这里， $s pl i t$ 和 $c a t$ 分别表示沿着通道维度对特征图进行分割和连接的操作， $s(x_{1})$ 和 $t(x_{1})$ 是由可学习神经网络[11]所预测出来的变换系数。

由于公式 $(3)$ 中的最大似然损失会推动所有的 $z$ 去拟合 $\mathbb{I})$ 分布，所以模型并不需要对不同的类特征进行区分。

因此，模型更有可能会产生一种偏差，即预测所有的 $s(\cdot)$ 为非常小的负数（趋近于 $-\infty$ ）并且 $t(\cdot)$ 接近零。

	在这个归一化流模型的一层耦合层中，有 $ s(x_{1}) $ 和 $t(x_{1})$ 这两个变换系数。
	
	当模型在训练时，由于要让所有的潜在变量 $z$ 符合标准正态分布 $N(0, \mathbb{I})$，它可能就会走“捷径”，让 $s(x_{1})$ 变得非常小（接近负无穷），$t(x_{1})$ 接近零。
	
	公式中 $z_{2}=x_{2} \odot exp \left(s\left(x_{1}\right)\right)+t\left(x_{1}\right)$ 这部分，当 $s(x_{1})$ 接近负无穷时，$exp \left(s\left(x_{1}\right)\right)$ 就会趋近于零，那么 $x_{2} \odot exp \left(s\left(x_{1}\right)\right)$ 这一项也就趋近于零了，再加上 $t\left(x_{1}\right)$ 接近零，所以 $z_{2}$ 就会趋于零。
	
	而整个 $z$ 是由 $z_{1}$ 和 $z_{2}$ 组成的，$z_{2}$ 趋于零了，那这一层的输出 $z$ 也就会趋于零。
	
	这样一来，不同类别的特征经过这一层后，输出都很相似，都趋于零，就好像被“同质化”了，这就是所谓的“同质映射”问题，会导致模型无法很好地区分正常和异常特征。

这种情况所带来的影响就是，模型即便在存在偏差的情况下，也能够将 $x_{a}$ 很好地拟合到 $\mathbb{I})$ 分布中，从而导致无法检测出异常情况。

然而，如果我们将不同的类特征映射到不同的类中心，那么模型就更难以简单地采取这种存在偏差的解决方案。

相反， $s(\cdot)$ 和 $t(\cdot)$ 就必须要与输入特征呈现出高度的相关性。

考虑到在经过训练的模型中， $s(\cdot)$ 和 $t(\cdot)$ 是与正常特征相关联的，所以模型就无法很好地对 $x_{a}$ 进行拟合。

我们认为上述这种粗略的分析同样也可以应用到多层的情况当中。

因为当某一层的 $s(\cdot)$ 和 $t(\cdot)$ 存在偏差时，该层的输出将会趋于零。

从公式 $(4)$ 中可以看出，当一个耦合层的日前输出接近零的时候，下一层的输出也将会趋于零。

所以，经过多层之后的输出将会趋于零，整个网络依然会存在偏差。

在这里插入图片描述

3.3分层高斯混合归一化流建模

在这里插入图片描述

概述

正如图3所展示的那样，我们所提出的HGAD（分层高斯混合归一化流建模方法用于统一异常检测）是由特征提取器、归一化流模型（在附录C中有关于其详细信息）以及分层高斯混合建模这几个部分所组成的。

首先，由固定的预训练骨干网络所提取出来的特征会被送入到归一化流模型当中，经过处理后转换为潜在嵌入。

然后，我们会在训练期间采用分层高斯混合建模方法来对这些潜在嵌入进行拟合。

在图3中，我们仅仅展示了一个层级的特征情况，但实际上我们是提取了多级的特征图，并且在每一个层级上都构建了NF模型。

我们的HGAD的伪代码在算法1中给出。

类间高斯混合建模

正如在3.2节中所讨论的那样，将不同类别的特征映射到不同的类中心能够在一定程度上减轻对数似然偏差问题。

为此，为了能够更好地拟合潜在空间中那种复杂的多类正态分布，我们提出了类间高斯混合建模方法。

具体来说，我们使用具有类别相关均值 $\mu_{y}$ 和协方差矩阵 $\sum_{y}$ （这里的 $y$ 是用于区分不同类别的标识）的高斯混合模型作为潜在变量 $Z$ 的先验分布，其表达式如下：
$p_{Z|Y}(z|y)=\mathcal{N}(z; \mu_{y}, \sum_{y}) \quad \text{且} \quad p_{Z}(z)=\sum_{y} p(y)\mathcal{N}(z; \mu_{y}, \sum_{y}) \quad(5)$

为了简化处理过程，我们同样也会使用单位矩阵 $\mathbb{I}$ 来替换所有类别相关的协方差矩阵 $\sum_{y}$ 。

为了促使网络能够自适应地学习类别权重，我们通过可学习向量 $\psi$ 来对类别权重 $p (Y)$ 进行参数化处理，其中 $p(y)=softmax_{y}(\psi)$ ，这里的 $so f t ma x$ 算子的下标 $y$ 表示是针对类别索引 $y$ 来计算 $so f t ma x$ 值的。

通过使用 $so f t ma x$ 函数可以确保 $p (y)$ 的值为正，并且所有类别权重的总和为1。 $\psi$ 可以初始化为0。

通过这种参数化的 $p (Y)$ ，我们能够推导出类间高斯混合建模的损失函数如下（详细的推导过程在附录E中给出）：
在这里插入图片描述

在这里， $c_{y}$ 表示对数类别权重，其定义为 $KaTeX parse error: Undefined control sequence: \logsoftmax at position 18: …{y}:=\log p(y)=\̲l̲o̲g̲s̲o̲f̲t̲m̲a̲x̲_{y}(\psi)$ ， $KaTeX parse error: Undefined control sequence: \logsumexp at position 1: \̲l̲o̲g̲s̲u̲m̲e̲x̲p̲$ 算子的下标 $y$ 表示是对所有类别的 $e x p$ 值进行求和操作。

互信息最大化

接下来，我们进一步认为类间高斯混合建模仅仅只能确保潜在特征被吸引到整个分布（这个分布是由 $\{\mu_{y}, \psi_{y}\}_{y = 1}^{Y}$ 这些参数所参数化的）当中，其中 ${p(y)\}_{y = 1}^{Y}$ 能够控制不同类中心对对数似然估计值 $\log p_{\theta}(x)$ 的贡献。

这也就意味着公式 $(6)$ 中的损失函数仅仅只有吸引特性，它能够促使潜在特征去拟合多模态分布，但却并没有那种用于分离不同类别的排斥特性，这样依然会导致对不同类特征的判别能力相对较弱。

由于类中心是随机初始化的，这就有可能导致不同的类中心坍缩到同一个中心。

为了解决这个问题，我们认为来自类别 $y$ 的潜在特征 $z$ 应该尽可能地靠近其相应的部位类中心 $\mu_{y}$ ，同时还要远离其他类中心。

从信息论的角度来看，这就意味着互信息 $I (Y, Z)$ 应该足够大。

因此，我们提出了一个互信息最大化损失，其目的是为了引入类排斥特性，以此来提高类判别能力。损失函数的定义如下（详细的推导过程在附录E中给出）：
$\mathcal{L}_{mi}=-\mathbb{E}_{y\sim p(Y)}[- \log p(y)]-\mathbb{E}_{(x, y)\sim p(X, Y)}[\log \frac{p(y)p(\varphi_{\theta}(x)|y)}{\sum_{y'}p(y')p(\varphi_{\theta}(x)|y')}] \quad(7)$

通过在公式 $(7)$ 中用 $N(\varphi_{\theta}(x); \mu_{y}, I)$ 替换 $p(\varphi_{\theta}(x)|y)$ ，我们能够推导出以下这种实际的损失形式（详细的推导过程在附录E中给出）：
$\mathcal{L}_{mi}=-\mathbb{E}_{(x, y)\sim p(X, Y)}[\log_{y}(-\frac{\parallel \varphi_{\theta}(x)-\mu_{y'}\parallel_{2}^{2}}{2}+c_{y'})-c_{y}]$

在这里， $\mu_{y'}$ 表示除了 $\mu_{y}$ 之外的所有其他类中心， $c_{y}$ 表示除了 $c_{y}$ 之外的所有其他对数类别权重， $KaTeX parse error: Undefined control sequence: \logsoftmax at position 1: \̲l̲o̲g̲s̲o̲f̲t̲m̲a̲x̲$ 的下标 $y$ 表示是针对类别 $y$ 来计算 $KaTeX parse error: Undefined control sequence: \logsoftmax at position 1: \̲l̲o̲g̲s̲o̲f̲t̲m̲a̲x̲$ 值的。

需要注意的是，在接下来的部分（例如公式 $(9)$ ）中，我们同样也会采用这种表示方式来进行 $so f t ma x$ 计算。

除了上述所提到的互信息最大化损失之外，我们还提出可以通过最小化类间熵来引入类排斥特性。

我们使用 $-\frac{\parallel \varphi_{\theta}(x)-\mu_{y}\parallel_{2}^{2}}{2}$ 作为类别 $y$ 的类别对数几率，然后依据一个标准的熵公式来定义熵损失如下：
$KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: …2} / 2)\right]$

学习类内混合类中心

在现实场景当中，即便是针对一个对象类别而言，也有可能会包含多种正常模式。

因此，为了能够更好地对类内分布进行建模，我们进一步将高斯先验 $p(Z|y)=N(\mu_{y}, \sum_{y})$ 扩展为混合高斯先验 $p(Z|y)=\sum_{i = 1}^{M} p_{i}(y)N(\mu_{i}^{y}, \sum_{i}^{y})$ ，其中 $M$ 表示类内潜在中心的数量。

我们可以直接将公式 $(5)$ 中的 $p (Z ∣ y)$ 进行替换，并且推导出公式 $(6)$ 中相应的损失函数 $L_{g}$ （具体的推导过程可以在附录式 $(7)$ 中查看）。

然而，初始的潜在特征 $Z$ 通常与类内中心 $\{\mu_{i}^{y}\}_{i = 1}^{M}$ 之间存在着较大的距离，这将会导致 $p (z ∣ y)$ （其中 $\in Z$ ）的值接近零。

在计算对数函数之后，很容易就会导致损失在数值上定义不明确（出现NaN情况），这样就使得其无法进行优化。

为此，我们建议将类间高斯混合建模和类内潜在中心学习这两个过程进行解耦。

这种解耦策略对于学习类中心是更为有利的，因为我们由此形成了一个从粗到细的优化过程。

具体来说，对于每一个类别 $y$ ，我们会学习一个主类中心 $\mu_{1}^{y}$ 和增量向量 $\{\Delta \mu_{i}^{y}\}_{i = 1}^{M}$ （其中 $\Delta \mu_{1}^{y}$ 固定为0），它们表示的是与主中心的偏移值，并且是用于表示其他类内中心的，其关系如下：
$\mu_{i}^{y}=\mu_{1}^{y}+\Delta \mu_{i}^{y} \quad \text{for} \quad i = 1, \cdots, M$

然后，我们可以直接使用公式 $(6)$ 来对主中心 $\mu_{1}^{y}$ 进行优化。

在学习其他类内中心时，我们会将主中心 $\mu_{1}^{y}$ 从梯度图中分离出来，仅仅通过以下的损失函数来对增量向量进行优化：
$\mathcal{L}_{in}=\mathbb{E}_{(x, y)\sim p(X, Y)}\left[-\log \sup_{i} exp \left(-\frac{\parallel \varphi_{\theta}(x)-(SG[\mu_{1}^{y}]+\Delta \mu_{i}^{y})\parallel_{2}^{2}}{2}+c_{i}^{y}\right)-\log \vert\det J\vert\right]$

在这里， $SG[\cdot]$ 表示停止梯度反向传播， $c_{i}^{y}$ 表示对数类内中心权重，其定义为 $c_{i}^{y}:=\log p_{i}(y)=\log softmax_{i}(\psi_{y})$ 。

请注意， $\psi_{y} \in \mathbb{R}^{M}$ 是特定于类别 $y$ 的， $\psi \in \mathbb{R}^{Y}$ 是用于整个分布的。

总体损失函数

总体训练损失函数是公式 $(6)$ 、公式 $(8)$ 、公式 $(9)$ 和公式 $(10)$ 的组合，如下所示：
$\mathcal{L}=\lambda_{1}\mathcal{L}_{g}+\lambda_{2}\mathcal{L}_{mi}+\mathcal{L}_{e}+\mathcal{L}_{in} \quad(11)$

其中 $\lambda_{1}$ 和 $\lambda_{2}$ 用于权衡损失项，默认设置为1和100。 $\mathcal{L}_{e}$ 和 $\mathcal{L}_{in}$ 用作辅助损失，因此我们不对它们进行加权因子的消融实验，因为这会导致太多的组合实验。

在附录A.1中，我们进一步解释了我们方法中各个组件相互连接的必要性和动机。

3.4异常评分

在这里插入图片描述

如算法1所示，我们实际上提取了(K)级特征图，并在每一级构建了(NF)模型。对于来自第(k)级的每个测试输入特征(x^{k})（(k \in K)），我们可以计算其类内对数似然(\log p_{\theta}(x^{{k}))以及类间负熵(nh(x}{k}))，具体计算方式如下：

类内对数似然(\log p_{\theta}(x^{k}))的计算公式为：
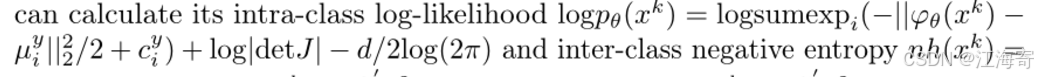
在这里插入图片描述

在这里插入图片描述

3.5进一步讨论

明确区分类别

我们的方法利用了每个图像的类别(y)，但与一对一的(AD)模型相比，它不会引入任何额外的数据收集成本。

现有的(AD)数据集是为一对一的异常检测收集的（即我们需要为每个类别训练一个模型）。因此，现有的(AD)数据集需要根据类别进行分离，每个类别作为一个子数据集。

所以，一对一的(AD)方法也需要区分类别，因为它们需要来自同一类别的正常样本来训练。

我们的方法实际上与这些方法具有相同的监督。不同之处在于我们明确区分类别，而它们没有明确区分类别。

因此，我们的方法仍然遵循与一对一(AD)模型相同的数据组织格式。但是我们统一(AD)方法的优点是我们可以为所有类别训练一个模型，大大降低了训练和部署的资源成本。

此外，我们的方法只需要分离不同的类别，不需要像素级别的注释。对于现实世界的工业应用，这不会产生额外的数据收集成本，因为我们通常有意识地根据不同类别收集数据。

在附录A.2中，我们详细总结了我们的方法和其他方法所需的样本和监督信息。

与其他利用类别信息方法的比较

(PMAD) [34]使用类别信息，(UniAD) [35]和(OmniAL) [41]使用额外信息来模拟异常。虽然我们也使用类别信息，但我们的方法可以取得比这些方法更好的结果。

因此，我们认为是否利用类别信息不应成为统一(AD)建模的严格限制，特别是当类别信息已经存在时。

关于“相同快捷方式”问题的讨论

在附录A.3中，我们进一步提供了关于“相同快捷方式”问题的更多讨论，并指出“同态映射”本质上不等于“相同快捷方式”问题。

与(UniAD)相比，我们的方法是在基于归一化流的异常检测方向上对统一异常检测的有效探索。

在附录A中，我们还进一步讨论了我们方法的局限性、应用、有效保证和复杂性。我们还在附录F中提供了一个信息论的观点。

4 实验

4.1 数据集和指标

数据集：我们在四个真实世界的工业异常检测数据集上广泛评估了我们的方法：MVTecAD、BTAD、MVTec3D - RGB和VisA。这些数据集的详细介绍见附录D。为了更充分地评估不同异常检测模型的统一异常检测性能，我们将这些数据集组合成一个40类的数据集，我们称之为Union数据集。
指标：遵循先前的工作，我们使用异常检测中的标准指标AUROC来评估异常检测方法的性能。

4.2 主要结果

设置：对于每个数据集，我们使用来自不同类别的图像训练一个统一模型。我们使用Efficient - b6作为特征提取器。在训练过程中冻结特征提取器的参数。NF模型的层数均为12。类间中心的数量始终等于数据集中的类别数量。
所有数据集的类内中心数量均设置为10（见4.3节的消融研究）。
我们使用带有权重衰减 $1e^{-4}$ 的Adam优化器来训练模型。默认情况下，总训练轮数设置为100，批量大小为8。初始学习率为 $2e^{-4}$ ，在[48, 57, 88]轮后下降0.1。评估使用3个随机种子进行。
基线：我们将我们的方法与一对一的异常检测基线进行比较，包括：PaDiM、MKD和DRAEM，以及最先进的统一异常检测方法：PMAD、UniAD和OmniAL。我们还与最先进的一对一基于NF的异常检测方法：CFLOW和FastFlow进行比较。在统一情况下，一对一异常检测基线和基于NF的异常检测方法的结果是使用公开可用的实现运行的。
定量结果：MVTecAD上的详细结果见表1。我们还在附录表3中报告了一对一设置下的结果。通过比较可以看出，所有基线和最先进的一对一基于NF的异常检测方法在统一情况下的性能都大幅下降。然而，我们的HGAD在统一情况下显著优于所有基线。与一对一基于NF的异常检测方法相比，我们将统一异常检测性能从91.8%提高到98.4%，从96.0%提高到97.9%。我们进一步指出，我们的模型与CFLOW具有相同的网络架构，**我们只是引入了多个类间和类内中心作为额外的可学习参数。**这意味着我们的新颖设计是提高基于NF的异常检测方法统一异常检测能力的关键。此外，我们的HGAD也超过了最先进的统一异常检测方法，PMAD（提高了3.9%和2.3%）和UniAD（提高了1.9%和1.1%），证明了我们的优越性。此外，BTAD、MVTec3D - RGB、VisA和Union数据集上的结果（见表2）也验证了我们方法的优越性，在异常检测方面，我们分别比UniAD高出0.9%、9.6%、4.3%和6.6%。
定性结果：图4显示了定性结果。可以发现，即使对于不同的异常类型，我们的方法也能比一对一基于NF的基线CFLOW生成更好的异常分数图。更多定性结果见附录图2。

4.3 消融研究

层次高斯混合建模：
- 表3a验证了我们的确认，即映射到多个类中心是有效的。使用固定的多个中心（FMC，仅基于固定的多个中心但没有高斯混合建模），图像级和像素级AUROC分别可以提高4.1%和1.8%。通过采用类间高斯混合建模来学习潜在的多类分布，AUROC可以进一步提高1.4%和0.9%。
- 表3a证明了互信息最大化（MIM）的有效性，其中添加MIM对检测带来了1.8%的提升。这表明为了更好地学习复杂的多类分布，有必要赋予模型类判别能力，以避免多个中心坍缩到同一个中心。
- 表3a证实了类内混合类中心学习的功效。以FMC为基线，引入学习类内混合类中心可以分别使检测和定位提高1.6%和1.0%。最后，将这些结合起来，我们形成了层次高斯混合建模方法以获得最佳结果。
类内中心数量：我们进行实验以研究每个类中类内中心的影响。结果见表3b。最佳性能是在中等数量（10个类中心）时实现的。像20这样更大的类中心数量并没有带来进一步的提升，这可能是因为类中心已经饱和，更多的类中心更难训练。对于其他数据集，我们也使用10作为类内中心的数量。
异常标准：仅将对数似然和熵作为异常标准可以获得良好的性能，而我们的相关标准始终优于每个标准。这说明相关的异常评分策略更有利于保证异常被识别为分布外。
超参数：我们在表3d中消融了超参数 $\lambda_{1}$ 和 $\lambda_{2}$ 。请注意，表3a、b、c和e中的实验是在 $\lambda_{1}$ 和 $\lambda_{2}$ 设置为1和10的情况下进行的。表3d中的结果表明，较大的 $\lambda_{2}$ 可以实现更好的统一异常检测性能。较大的 $\lambda_{2}$ 可以促使网络更专注于将不同的类特征分离到它们相应的类中心，这表明类判别能力对于完成统一异常检测至关重要。
优化策略：我们发现一开始同时优化类间和类内中心会带来不稳定性。因此，我们采用了两阶段优化策略（详见附录C）。该策略可以更好地解耦类间和类内学习过程，从而带来更好的结果。