树和森林
一、树的存储结构
- 树,在实现时无论采取的是顺序存储还是链式存储,都
必须做到唯一反映树中各节点之间的逻辑关系。树的常用的表示方法有三种,分别是双亲表示法、孩子表示法和孩子兄弟表示法。
1、双亲表示法
以一组连续的存储单元存储树的结点,每个结点除了数据域 data 外,还设有 parent 域用于指示其双亲结点,形式如下:

- 其抽象数据类型如下(纯理论学习,不实现)
typedef struct TreeNode { int data; int parent; }; typedef struct Tree { TreeNode nodes[size]; int n; }; - 与二叉树的顺序存储结构的区别:
对于树,数组下标代表结点编号,下标中所存的内容指示了各节点之间的关系;对于二叉树,数组下标既代表节点编号又指示了各节点之间的关系。二叉树都可用树的存储结构来存储,但树不能用二叉树的存储结构来存储。其实,树与二叉树就是一般与个别的关系,个别所有的性质在一般里都可以找到,但一般有的性质在个别里就不一定有。
2、孩子表示法
-
该法,
是将每个结点的孩子结点都用单链表链接起来形成一个线性结构,n 个节点就有 n 个孩子链表,其形式如下:

-
上图对应的二叉树如下:
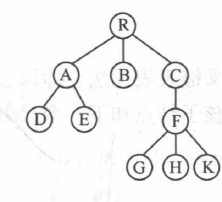
-
这种存储结构,对寻找子女的操作极其方便,却不利于寻找双亲,
寻找双亲需要遍历n个节点中孩子链表指针域所指向的 n 个孩子链表。
3、孩子兄弟表示法
- 此法又称为
二叉树表示法,以二叉链表作为树的存储结构。 - 此法中的树节点由数据域和两个指针域组成,两个指针域分别指向
第一个孩子节点和下一个兄弟节点。


- 其节点代码如下:
typedef struct TreeNode { int data; TreeNode *firstchild, *nextsibling; }; - 此种存储结构,对
进行树转换二叉树的操作极其方便,且易于查找结点的孩子;不足之处在于查找当前节点的双亲。
二、树或森林转二叉树
- 首先,毫无疑问的是,根据一定规则,任何一棵树都可以转为对应的二叉树的。这是因为:
二叉树和树都可以用二叉链表表示,故而通过二叉链表可以找到树与二叉树的一一对应关系。
1、规则
- 树转二叉树的规则:
每个节点左指针指向它的第一个孩子,右指针指向它在树中相邻的右兄弟,此规则称为左孩子右兄弟规则。根据该规则,由于根节点没有兄弟,所以对应的二叉树是没有右子树的。 - 森林转二叉树规则与树的类似,
先间森林中的每棵树转为二叉树,由于树对应的二叉树都是没有右子树的,因此可以将森林中的第二棵二叉树视为目标二叉树的根节点的右子树,将第三棵视为第二棵的右子树……以此类推。

2、画法与算法思想
2.1、画法
- 指将树或森林转为二叉树的画法。
- 1)
树转换成二又树的画法:①在兄弟结点之间加一连线;②对每个结点,只保留它与第一个孩子的连线,而与其他孩子的连线全部抹掉;③以树根为轴心,顺时针旋转45°。 - 2)森林转换成二又树的画法:①将森林中的每棵树转换成相应的二又树;②每棵树的根也可视为兄弟关系,在每棵树的根之间加一根连线:③以第一棵树的根为轴心顺时针旋转45°。
2.2、算法思想

- 根据上述算法思想,利用递归定义可以编写出将树或森林转换为二叉树的相关程序。
三、树和森林的遍历
1、树的遍历
- 树的遍历方式有两种,分别是
先根遍历和后根遍历。
1.1、先根遍历
- 先根遍历的规则如下:
1)若根非空,则先访问根节点,再依次遍历根节点每棵树。
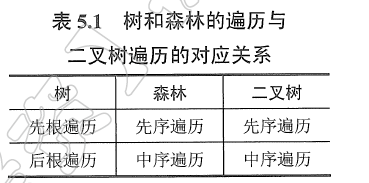
2)遍历子树时,遵循先根遍历原则。 - 树的先根遍历所得到的序列,与二叉树的先序遍历序列一样。
1.2、后根遍历
- 其规则如下:
1)若树非空,先依次遍历根节点的每棵子树,再访问根节点。
2)遍历子树时遵循后根遍历原则。 - 树的后根遍历序列与二叉树的中序遍历序列一样。
2、森林的遍历
- 森林遍历有两种方式:
先序遍历和中序遍历。
2.1、先序遍历森林
- 若森林非空,则按如下规则遍历森林的节点:
①访问森林中第一棵树的根结点;
②先序遍历第一棵树的根结点的子树森林;
③先序遍历除去第一棵树之后剩余的树构成的森林。
2.2、中序遍历森林
- 若森林非空,则可按下述规则遍历
①中序遍历森林中第一棵树的根结点的子树森林;
②访问第一棵树的根结点;
③中序遍历除去第一棵树之后剩余的树构成的森林。
四、并查集
- 并查集是树的一种应用,是一种简单的集合表示,支持如下操作:
1) Union(S,Root1,Root2):把集合S中的子集合Root2并入子集合Root1.要求Root1和Rot2互不相交,否则不执行合并。
2)Find(S,x):査找集合s中单元素x所在的子集合,并返回该子集合的名字。
3) Initial(S):将集合S中的每个元素都初始化为只有一个单元素的子集合。 - 通常用树(森林)的双亲表示作为并査集的存储结构,每个子集合以一棵树表示。所有表示子集合的树,构成表示全集合的森林,存放在双亲表示数组内。通常用数组元素的下标代表元素名,用根结点的下标代表子集合名,根结点的双亲结点为负数。
- 例如,若设有一个全集合为S={0,1,2,3,4,5,6,7,8,9},初始化时每个元素自成一个单元素子集合,每个子集合的数组值为-1,如图所示。

- 经过一段时间的计算,这些子集合合并为3个更大的子集合S={0,6,7,8},S2={1,4,9,S3={2,3,5},此时并查集的树形表示和存储结构如图所示。

- 为了得到两个子集合的并,只需将其中一个子集合根结点的双亲指针指向另一个集合的根结点。因此,S1US2可以具有如图所示的表示。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










