LL1文法、LR(0)文法、SLR文法、LR(1)文法、LALR文法

自顶向下分析

自顶向下分析指的是最左推导，最右归约是最左推导的逆过程，在最左推导中，总是选择每个句型的最左非终结符进行替换

---

自底向上分析

自底向上分析指的是最右推导、最左归约是最右推导的逆过程，在最右推到中，总是选择每个句型的最右非终结符进行替换

文法转换

• 回溯问题
• 直接左递归和间接左递归问题

回溯是指：同一非终结符的多个候选式存在共同前缀。例如：S —> aAd | aBe 该文法存在回溯现象

A —> Aa | β (a ≠ ε, β不以A开头)
=> Aaaaaaa
=>  βaaaaaa
消除直接左递归:
A —>  βA'
A' —> aA' | ε

S —> Aa | b
A —> Ac | Sd | ε
消除间接左递归:
A —> Ac | Aad | bd | ε
消除间接左递归:
A —> bdA' | A'
A' —> cA' | adA' | ε

---

LL(1)文法

LL1文法可以解决回溯，被称为预测分析

S 文法

	S文法不含有ε产生式

• 每个产生式的右部都以终结符开始
• 同一非终结符的各个候选式的首终结符都不同

ε产生式的使用

ε产生式的使用取决于非终结符后面的终结符(这里的终结符可能是一个也可能是多个)

如果当前非终结符A与要输入的符号a 不匹配时，若存在A—>ε,可以通过检查a是否可以出现在A的后面，来决定是否使用A—>ε (若文法中没有A—>ε，则应报错）

非终结符的后继符号集

紧接非终结符后面的终结符的集合称为非终结符的后继符号集，记为FOLLOW(该非终结符)

产生式的可选集

产生式的可选集也称为select集，指的是推导输入串时可用的产生式的集合

SELECT(A—> aβ) = { a }  a为首终结符
SELECT(A—>ε) =  FOLLOW(A) 

Q文法

q文法不含右部以非终结符打头的产生式

• 每个产生式的右部是以ε开始或者以终结符开始
• 具有相同左部的产生式有不相交的可选集

串首终结符集

串首终结符是指产生式右部第一个终结符，串首终结符也可以是ε。串首终结符的集合称为串首终结符集也称First集

如果ε ∉ First(α), 那么SELECT(A—>α) = First(α)
如果ε ∈ FIRST(α),那么SELECT(A—>α) = (FIRST(α) - {ε}) ∪ FOLLOW(A)

LL(1)文法

第一个L是从左向右扫描输入，第二个L是产生最左推导，1是指需要向前看一个输入符号来决定语法分析动作

文法G是LL(1)的，当且仅当G的任意两个具有相同左部的产生式A —>α | β 满足：
1.不存在终结符a使得α 和 β 都能够推导出以a开头的串 (相当于前缀要不一样)
2.α 和 β至多有一个能推导出ε (如果都包含空串，SELECT集就像相交了)
3.如果 β => ε，则FIRST(α) ∩ FOLLOW(A) = Φ
     α => ε，则FIRST(β) ∩ FOLLOW(A) = Φ
保证同一非终结符的各个产生式的可选集互不相交

---

SELECT集、FOLLOW集、FIRST集计算

FIRST集计算

First(X): 可以从X推导出的所有 串首终结符的集合 ，包括ε

E —> TE’
T ‘—> *FT’ | $ϵ$
E’ —> +TE’ | $ϵ$
F —> ( E ) | id
T —> FT’
求FIRST集：(找最左终结符)
FIRST(E） = FIRST(T) = FIRST(F) = { ( id }
FIRST(E’) = { + $ϵ$ }
FIRST(T’) = { * $ϵ$ }

如果产生式的右部遇到的不是终结符，是非终结符的话就从该非终结符产生式的右部找起

FOLLOW集计算

FOLLOW(A): 跟在非终结符A后面的总结符的集合，若A是文法的开始符，那么就需要把$或者#(代表结束符)加入到FOLLOW(A)中

• 第一种就是该非终结符后面是终结符，那么该终结符属于该非终结符的FOLLOW集
• 第二种是该非终结符在产生式最右边，该非终结符的FOLLOW集需要∪产生式左部非终结符的FOLLOW集
• 第三种该非终结符的后面不是终结符而是一个非终结符则看此终结符的产生式，如果此终结符的产生式可以为空，那么该非终结符的FOLLOW集就是后面的非终结符的FIRST(此终结符) -ϵ ∪ FOLLOW(此终结符）

E —> TE’
T ‘—> *FT’ | $ϵ$
E’ —> +TE’ | $ϵ$
F —> ( E ) | id
T —> FT’

FOLLOW(E) = FOLLOW(E’） = {) #}
FOLLOW(E‘） = FOLLOW(E) = { ) # } E’出现在最右部
FOLLOW(T） = {FIRST(E’) - $ϵ$} $\cup$ FOLLOW(E’)} = { + ） # }
FOLLOW(T’) = FOLLOW(T) = { +) # }
FOLLOW(F) = { FIRST(T’) - $ϵ$} $\cup$ FOLLOW(T’) } = {* +) # }

SELECT集计算

SELECT集是针对产生式的，需要将具有相同产生式左部的产生式展开，根据公式计算SELECT集

(1)E —> TE’
(2)T ‘—> *FT’
(3)T’ —> $ϵ$
(4)E’ —> +TE’
(5)E’—> $ϵ$
(6)F —> ( E )
(7)F—> id
(8)T —> FT’

SELECT(1) = {看的是T的终结符} = FIRST(T) = { ( id } 没有ε
SELECT(2) = {公式SELECT(A—> aβ) = { a } a为首终结符} = {*}
SELECT(3) = {公式SELECT(A—>ε) = FOLLOW(A)} = FOLLOW(T’) = {+ ) #}
SELECT(4) = {公式SELECT(A—> aβ) = { a } a为首终结符} = {+}
SELECT(5) = {公式SELECT(A—>ε) = FOLLOW(A)} = FOLLOW(E’)= { ) #}
SELECT(6) = {公式SELECT(A—> aβ) = { a } a为首终结符} = {(}
SELECT(7) = {公式SELECT(A—> aβ) = { a } a为首终结符} = {id}
SELECT(8) = {看的是F的终结符} = FIRST(F) = {( id } 没有ε

如果FIRST集里面有ε，就用公式ε ∈ FIRST(α),那么SELECT(A—>α) = (FIRST(α) - {ε}) ∪ FOLLOW(A)

预测分析表

根据SELECT集填表格，横向是终结符，纵向是非终结符

-	id	+	*	(	)	#
E	E —> TE’			E —> TE’
E’		E’ —> +TE’			F —> ( E )	F —> ( E )
T	T —> FT’			T —> FT’
T’		T’ —> $ϵ$	T ‘—> *FT’	T’ —> $ϵ$	T’ —> $ϵ$	T’ —> $ϵ$
F	F—> id			F —> ( E )

例子

S —> (L) | a
L —> SL’
L’ —> ,SL’ | ϵ

FIRST(S) = {(,a}
FIRST(L) = {(,a}
FIRST(L’) = {, ϵ}

FOLLOW(S) = {$,)}
FOLLOW(L) = { ) }
FOLLOW(L’) ={ ) }

…略

---

递归预测分析法

递归预测分析法预测分析法是指：在递归下降分析中，编写每一个非终结符对应的过程，根据预测分析表进行产生式的选择

---

非递归预测分析法

非递归的预测分析不需要为每一个非终结符编写递归下降过程，而是根据预测分析表构造一个自动机，也叫表驱动的预测分析

---

预测分析中的错误检测

错误

• 栈顶的终结符和当前输入符号不匹配
• 栈顶非终结符与当前输入符号在预测分析表对应项中的信息为空

处理

恐慌模式：

• 忽略输入中的一些符号，直到输入中出现由设计者选定的同步词法单元(synchromizing token)集合中的某个词法单元，同步集合的选取使得语法分析器能从实际遇到的错误中快速恢复，可以将FOLLOW(A)中的所有终结符放入非终结符A的同步记号集合

• 如果终结符在栈顶而不能匹配，一个简单的办法就是弹出此终结符

---

自底向上的语法分析

• 分析树的底部(叶节点)向顶部(根节点)方向构造分析树
• 将输入串w规约为文法开始符号S的过程
• 自顶向下语法分析采用最左推导方式, 自底向上语法分析采用最左规约方式(反向构造最右推导)
• 自底向上语法分析的通用框架是：移入-规约分析

移入-规约过程

堆栈内符号串 + 剩余输入 = 规范句型，规范句型相当于最右推导

移入-规约分析中存在的问题

每次规约的符号串是直接短语，造成错误的原因是错误的识别了句柄，也就是选错了产生式

• 直接短语：直接短语一定是产生式的右部，产生式的右部不一定是直接短语，并且是高度为二子树的边缘
• 句柄：句型的最左直接短语

---

LR分析法概述

可以用LR文法分析的文法叫做LR文法，LR文法是最大的、可以构造出相应移入-规约语法分析器的文法类

• L：对输入进行从左到右的扫描
• R：反向构造出一个最右推导序列
• LR(k) 需要向前查看k个输入符号的LR分析,一般k = 0 或者 k = 1

LR分析法的基本原理

• 自底向上分析的关键问题是什么？
  如何正确的识别句柄
• 句柄是逐步形成的，用“状态” 表示句柄识别的进展程度
  S—>bBB
  S—> •bBB (移进状态)
  S—>b•BB (待约状态)
  S—>bB•B (待约状态）
  S—>bBB• (规约状态)

LR分析器(自动机)的总体结构

LR分析表的结构

---

LR(0)分析法

右部某位置标有圆点的产生式称为相应文法的一个LR(0)项目，一个产生式有k个符号，就会有k+1个项目

增广文法

就是引入一个符号，使文法开始符号只出现在一个产生式的左边，从而使得分析器只有一个接受状态

文法中的项目

• 初始项目：圆点在最左边
• 规约项目：圆点在最右边
• 后继项目：两个项目之间间隔一个圆点

等价项目

当圆点后面是一个非终结符的时候，就会存在等价项目

项目集闭包

把所有的等价项目组成一个项目集(I),称为项目集闭包，每个项目集闭包对应着自动机的一个状态

LR(0)自动机

LR(0)自动机构造LR(0)分析表

根据上图的自动机得来的

LR(0)分析过程中的冲突

移进-规约冲突

无法确定是移进还是规约

规约-规约冲突

没有这两种冲突的文法是LR(0)文法，不是所有的上下文无关文法都可以用LR(0)文法分析

---

SLR分析

为了解决LR(0)分析过程中的冲突的问题(也就是识别句柄的问题),出现了SLR分析，也叫做SLR(1)分析，S是Simple的意思，简单的LR(1)

SLR分析基本思想

需要使用到FOLLOW集，在不知道是否移进或者规约时,向后查看一个输入符号，根据FOLLOW集的定义是：该终结符后面可以的跟的终结符的集合。

• 看规约项目产生式左部的非终结符的FOLLOW集，如果下一个输入符号在FOLLOW集中就规约
• 看移进项目的下一个终结符是和下一个输入符号一样，如果相同就移进
• 详情看图

例子

SLR分析中的冲突

如果产生式符合SLR分析基本思想的两种规则，就无法判定到底是移进还是规约

---

LR(1)分析法

SLR使用FOLLOW集可以排除一些问题，但是不能解决所有问题

LR(1)分析法的提出

产生式A—>a规约时，在不同的位置，要求有不同的后继符号，在特定位置时，A的后继符号集合是FOLLOW(A)的子集

LR(1)项目

• 将一个形式为[A—>α• β ,a]的项称为LR(1)项，其中A—>α β 是一个产生式，a是一个终结符(这里将$视为一个特殊的终结符)它表示在当前状态下，A后面必须紧跟终结符，称为该项的展望符
• LR(1)中的1指的是项的第二个分量的长度(就是向前查看一个符号)
• 在形如[A—>α• β,a]且β≠ ε的项中，展望符a没有任何作用
• 形如[A—>α•,a]的项在只有在下一个输入符号等于a时才可以安装A—>a进行规约，这样的a的集合总是FOLLOW(A)的子集，而且通常是一个真子集

LR(1)等价项目

LR(1)自动机

相比较LR(0)和SLR，多求了展望符，状态比较多

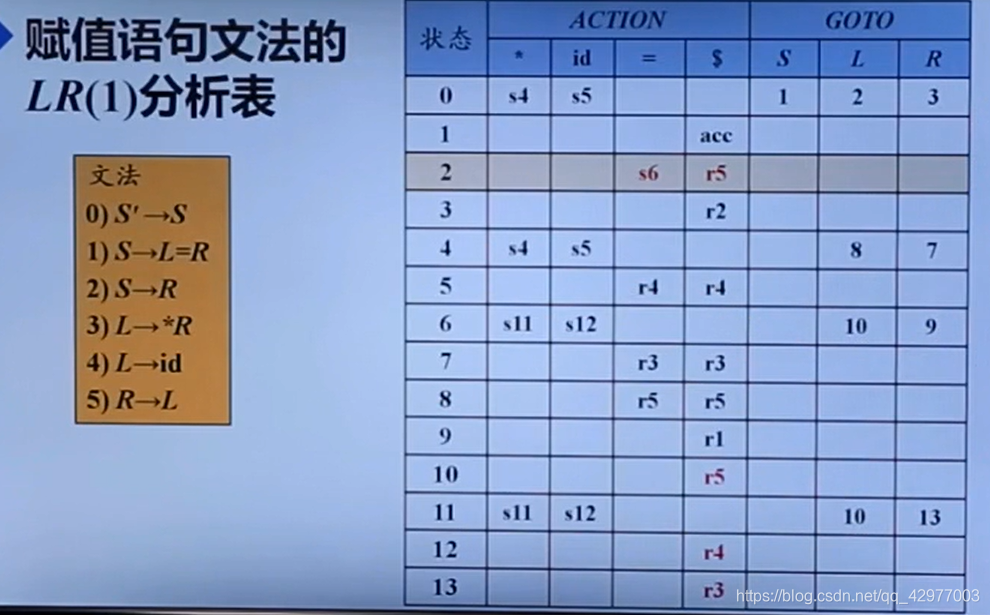
LR(1)分析表

---