三角形——推公式推到手抽筋的等边三角形

解析

不难想到，三角形三个顶点的排列情况应该有以下三种：

1.三点共线，显然无法组成三角形；

2.两点在同一条边上：

3.三点都在不同的边上：

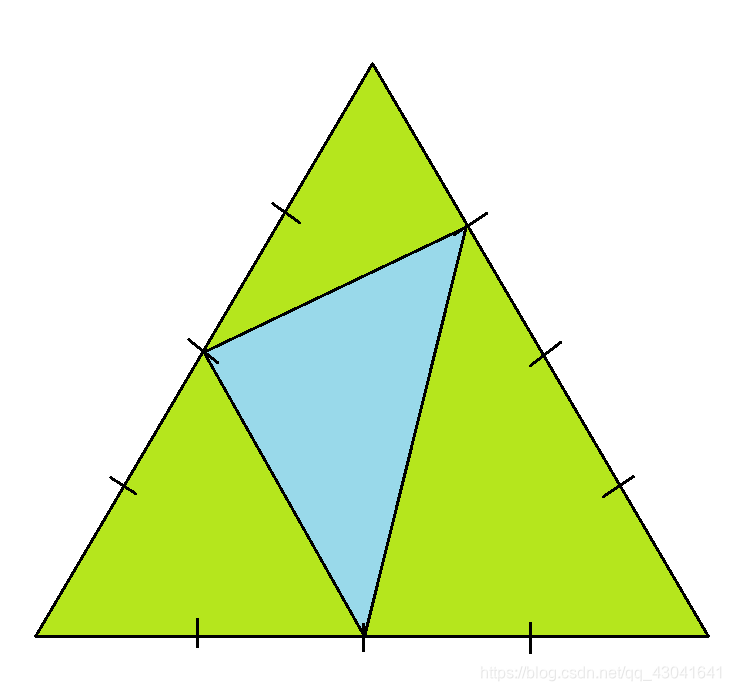
蓝色部分为我们选出来的三角形，绿色部分是剩余的三角形。

• 解法1

容易想出来的一种暴力的方法是，针对第一种三角形和第二种三角形分别处理。为了方便，我们先建立一个特殊的坐标系：

对于两点共边的三角形，枚举三个点的位置$i,j,k$设$i$和$j$在同一坐标轴上，为了防止重复，设$i$随时在$j$的后面，根据面积的定义，可以得到以下几行代码：

for(int i=1;i<=n;++i)
for(int j=i+1;j<=n;++j)
for(int k=1;k<=n;++k)
ans+=(j-i+1)*k;

于是面积就被很简单的暴力$O(n^3)$地算出来啦！

对于第二种情况，直接算选出的三角形的面积不好算，但是我们没选出来的部分构成了三个三角形，且比较好计算。所以我们可以通过计算周围三个三角形的方式，运用补集转化的思想，用整个三角形的面积减去周围小三角形的面积，求出中间的三角形的面积，设大三角形的面积为$S$，这里应注意一条边被我们分成了$(n+1)$分，所以$S=(n+1{)}^2$。

那么计算就很简单了，周围三个小三角形的面积分别是$i\times j$、$i\times k$和$j\times k$，代码如下，复杂度为$O(n^3)$：

for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
for(int k=1;k<=n;++k)
ans+=S-i*j-i*k-j*k;

• 解法2

显然，上面$O(n^3)$的方法最多只能过$30\%$的数据，而最大数据是$10^9$，会$TLE$得很惨。

略微思考一下，既然是$10^9$，那么多半是要推公式了。

再思考一下，答案就是两个式子的和：

对于第一种情况，将$i$轴看做底边，答案即是底为1的三角形的面积和+底为2的三角形面积和+···底为n的三角形面积和。动动手指头，底为1的三角形有$n-1$个，底为2的三角形有$n-2$个，···底为$n$的三角形有$1$个，即$n-(n-1)$个，而每个三角形的高（设为$k$）可以为$1$~$n$的任意一个数，所以推出公式为：
$$\sum _{k=1}^n(n-1)\times 1\times k+(n-2)\times 2\times k+\cdots +(n-(n-1))\times n\times k$$
将$k$提出来，得到：
$$\sum _{k=1}^{n}k\times [(n-1)\times 1+(n-2)\times 2+\cdots +(n-(n-1))\times n]$$
设$A={\sum }_{k=1}^n$，即$A=\frac{n(n+1)}{2}$，公式化简为：
$$A\times [(n-1)\times 1+(n-2)\times 2+\cdots +(n-(n-1))\times n]$$

$A$是已知的，现在讨论如何求：
$$(n-1)\times 1+(n-2)\times 2+\cdots +(n-(n-1))\times n$$
很明显，将$(n-1)、(n-2)$括号内的$1,2,\cdots ,n-1$提出来，用乘法分配律，得到：
$$n\times 1+n\times 2+\cdots n\times n-(1^2+2^2+\cdots +n^2)$$
用公式分别表示两边的式子，得到：
$$n\times A-\frac{n(n+1)(2n+1)}{6}$$
代入原式子，得到：
$$n\times A^2-\frac{n(n+1)(2n+1)}{6}\times A$$
代入$A$，化简，得到式子：
$$\frac{n^5+n^4-n^3-n^2}{12}$$
因为我们只讨论了$i$轴上的情况，一共有三个坐标轴，且每种情况的高可以在左边，也可以在右边，并且这些情况都不会重复（不懂得请自己简单证明），如图：

其中黑色边和红色边的三角形的面积相等，所以答案还要乘以6，即：
$$\frac{n^5+n^4-n^3-n^2}{2}$$

对于第二种情况，从刚才暴力的代码中我们可以明显地看出来我们要求的公式：
$$\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^{n}S-ij-jk-ik$$
其中$S=(n+1{)}^2$，提出$S$，得到：
$$n^3\times S-\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^{n}ij+jk+ik$$
其中$n^3\times S$很好求出来所以我们要求的只是：
$$\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^{n}ij+jk+ik$$
可以看出，这个式子的结果明显是与$n$有关的定值，为了简化公式，我们先假设$i,j$不变，只考虑$k$，即求：
$$\sum _{k=1}^{n}ij+jk+ik$$
其中$i,j$与式子无关，可以提出来，在因式分解，化简得：
$$nij+\sum _{k=1}^{n}k\times (i+j)$$
再化简，得：
$$nij+(i+j)\times \sum _{k=1}^{n}k$$
即
$$nij+(i+j)\times A$$
好了，现在我们抵消掉$k$的影响了，暴力枚举$i$和$j$，我们可以发现，我们要求的是以下式子的和：

现在考虑$i=1$的情况：

我们分别求$1\times 1\times n+1\times 2\times n+\cdots 1\times n\times n$和$(1+1)\times A+(1+2)\times A+\cdots +(1+n)\times A$。

对于$1\times 1\times n+1\times 2\times n+\cdots 1\times n\times n$，
把$1\times n$提取出来，就变成了$1\times n\times A$；
对于$(1+1)\times A+(1+2)\times A+\cdots +(1+n)\times A$，
拆开括号，变成$1\times n\times A+A^2$，
加起来就是$1\times n\times A+1\times n\times A+A^2$，
合并一下就是$2\times 1\times n\times A+A^2$。

所以我们可以将原式子的和转化为：
$$\sum _{i=1}^n(2\times i\times n\times A+A^2)$$
化简一下，就变成了
$$3n{A}^2$$
将$A$代入原式子，得到
$$\frac{n^5+2n^4+n^3}{4}$$

将两种情况的式子加起来，就得到了最终的表达式
$$\frac{3n^5+4n^4-n^3-2n^2}{4}$$
预处理出4的逆元，再用快速幂就求出了最终我们需要的答案，复杂度近似$O(1)$，是不是很简单呢？

代码

#include<cstdio>
#define ll long long
#define mod 1000000007
using namespace std;

ll n,ans;
ll inv=250000002;//4的逆元

ll quick(ll x,ll y)
{
	ll ret=1;
	while(y)
	{
		if(y&1)ret=(ll)(ret*x)%mod;
		x=(ll)(x*x)%mod;
		y>>=1;
	}
	return ret;
}

int main()
{
	scanf("%lld",&n);
	ans=((ll)(3*quick(n,5))%mod+(ll)(4*quick(n,4))%mod-quick(n,3)-(ll)2*quick(n,2))%mod;
	ans=(ll)(ans*inv)%mod;
	ans=(ans%mod+mod)%mod;
	printf("%lld",ans);
	return 0;
}

总结

这道题就是疯狂地推公式，但是从一些细节中我们可以总结出以下几点：
1.根据题目特性，判断是否分类讨论；
2.对于一些数据范围比较大的题目，想到正解的复杂度应是$O(\log n)$、$O(\sqrt{n})$或推出公式$O(1)$的；
3.在面对变量较多但是有一定共性的公式时，可以采用主元法，即只把一个看作一个变量，其余的看作常量，化繁为简，由大到小；
4.这些题的公式比较复杂，所以我们运算的正确率一定要高。