25年5月通信基础知识补充1：Jakes模型、多普勒频移、多普勒谱

看文献过程中不断发现有太多不懂的基础知识，故长期更新这类blog不断补充在这过程中学到的知识。由于这些内容与我的研究方向并不一定强相关，故记录不会很深入请见谅。

一、Jake’s模型原理详解

1.1 瑞利衰落

  在移动无线通信环境中，信号传播通常伴随显著的多径效应。由于建筑物、地面及其他障碍物对无线电波的反射、散射与绕射，发射信号在传播过程中会形成多条路径，每条路径具有不同的传播时延与入射角，最终以叠加形式到达接收端。

  当通信环境中缺乏占主导的视距路径（Line-of-Sight, LOS），如在高密度城区或地下空间，各径信号的幅度通常相近，且其相位由于路径差异呈现随机性叠加，进而导致瑞利衰落（Rayleigh fading）现象。

  在统计建模中，若复信道增益的实部与虚部均为零均值、方差相等、彼此独立的高斯随机变量，则其包络服从瑞利分布。这一模型很好地刻画了NLOS场景下的信道统计特性，因此广泛用于建模城市环境、室内通信及非直视微波链路等系统。

  若通信环境中存在较强的直射成分，则信道表现为LOS路径与瑞利衰落分量的叠加，适合采用**莱斯衰落（Rician fading）模型**进行建模。此时，K因子（即直射路径功率与散射路径功率之比）用于度量LOS成分的相对强度。

  在Clarke经典模型（1968年）中，假设移动终端被大量等效散射体环绕，来波方向在水平面上呈各向同性均匀分布，且各径平均功率相等。基于该模型可推导出瑞利包络分布、Jakes频谱形状、以及信道自相关函数等关键统计特性，也为后续TDL（Tapped Delay Line）多径模型提供理论基础。

1.2 多普勒频移

  在上述“各向同性散射”模型下，接收机从多个方向接收到强度相近的多径信号，满足产生瑞利衰落所需的随机叠加条件。此时，多普勒效应成为引发小尺度衰落时间变化的主要因素：由于发射端、接收端或散射体存在相对运动，信号在每条路径上会经历不同程度的频率偏移，称为多普勒频移。

  设载频为$f_c$，接收机沿某方向以速度$v$移动，则与该方向成角度${\theta }_i$的第\i$条入射路径，其产生的多普勒频移为：

$$f_i=f_{\text{max}}\cos ({\theta }_i)\text{\hspace{1em}(1)}$$

其中：

• $f_i$：第$i$条路径的多普勒频移；
• $f_{\text{max}}=\frac{v}{\lambda }=\frac{vf\_c}{c}$：最大多普勒频移，$\lambda$为载波波长，$c$为光速；
• ${\theta }_i$：该路径的入射角，相对于移动方向。

  由该公式可知，多普勒频移的理论范围为$[-f_{\max },f_{\max }]$，其数值依赖于各路径的入射角。

1.3 Jakes模型与功率谱

  Jakes模型以公式（1）为基础，进一步考虑各向同性散射条件下，不同路径频移的概率分布特性。虽然频移范围是对称的$[-f_{\max },f_{\max }]$，但其分布并非均匀，而是集中于边缘频率区域。最终形成典型的U形功率谱密度分布，即Jakes谱（经典多普勒谱）：

$$S(f)=\frac{1}{\pi f_{\max }\sqrt{1-(f/f_{\max }{)}^2}},|f|\le f_{\max }\text{\hspace{1em}(2)}$$

  超过该范围（$|f|>f_{\max }$）时，功率谱密度为零。

  由该表达式可见，频率靠近$\pm f_{\max }$时，功率谱密度迅速上升，理论上趋于无穷大（在实际中受限于系统带宽和滤波器响应）。这说明在移动通信系统中，由于各向同性散射的几何分布，信号频率更容易聚集在最大频移附近，而在中心频率（即零频移）附近相对较低。

  Jakes谱广泛用于建模NLOS环境下移动通信信道的多普勒统计特性，在性能评估、调制方案设计、信道估计与跟踪算法仿真中发挥重要作用。该谱形不仅适用于瑞利衰落仿真，还可用于设计低复杂度的瑞利过程生成器（如八正弦波叠加方法等）。

  需要强调的是，瑞利小尺度衰落通常与路径损耗、阴影衰落等大尺度效应叠加，共同决定无线信道特性。系统中的最大多普勒频移$f_{\max }$由接收机速度$v$与载波频率$f_c$共同决定：

  这意味着：在高速移动场景中，信道在1秒内可能经历100次甚至更多的衰落起伏，表现为快速变化的深衰落（可达30–40 dB）；而在低速场景中，信道变化则相对缓慢，更利于信道跟踪与反馈机制设计。

1.4 其他谱及应用场景总结

  在无线信道建模中，多普勒功率谱用于描述移动场景下信号频率扩散特性，其频谱形状直接影响信道模型的准确性。其中，平坦谱（Flat Spectrum）以矩形频谱为特征，在频带$([-f_d,f_d])$内功率均匀分布，常用于理想化多普勒扩展的理论分析；Jakes谱（Jakes Spectrum）由经典移动信道模型衍生，其功率密度在最大多普勒频移$f_d$附近呈现尖峰特性$(S_j(f)\propto 1/\sqrt{1-(f/f_d{)}^2})$，适用于高速移动引起的密集多普勒扩展场景（如城市环境）；高斯谱（Gaussian Spectrum）则通过指数衰减函数$(S_G(f)\propto e^{-(f/f_d{)}^2})$将能量集中于低频区域，更适合低速移动或复杂地形（如丘陵地区）下的平缓频移分布。三者分别从均匀、高频集中及低频主导的角度刻画了不同动态环境中的多普勒效应。
注：以下的图参考[1]

1.4.1 Jakes谱

• 适用场景：
  • 高速移动环境（如90 mph车速的城市场景）；
  • 密集多径环境（如城市中高楼反射导致多普勒扩展显著）；
  • 经典移动通信模型（Bell实验室验证，能量集中于最大多普勒频移$f_d$）。
• 理论依据：
    Jakes谱的功率密度在$f_d$附近最高，适用于接收端快速移动导致多普勒频移显著的情况（如车载通信、高速铁路）。
  

1.4.2 高斯谱

  高斯谱的数学表达式为：
$$S_G(f)=\frac{2{\sigma }^2}{\sqrt{\pi }{f}_d^2}\exp \left(-\frac{f}{f_d}\right)$$

• 适用场景：
  • 低速移动环境（如行人或低速车辆场景）；
  • 复杂地形（如丘陵地区，信号经多径散射后频移变化平缓）；
  • 低频主导的传播环境（如郊区或稀疏建筑区域）。

1.4.3 平坦谱

  平坦频谱具有矩形形状。为了获得所需的过程带宽，需要进行适当的缩放和限带处理。平坦频谱由以下公式描述：
$$S_f(f)=\{\begin{array}{ll}{\sigma }^2/f_d,& -f_d<f<f_d\\ 0,& \text{其他情况}\end{array}$$
其中，$({\sigma }^2)$ 为总信号功率，$(f_d)$ 为最大多普勒频率。

• 适用场景：
  • 理论分析与基准测试（如理想化多普勒扩展模型）；
  • 实验室仿真（均匀频移分布便于简化计算）；
  • 不适用于实际工程（城市/丘陵地形中失真严重，性能最差）。
• 理论依据：
  平坦谱在频带内均匀分布，缺乏实际环境中的频率选择性，仅作为对比参考。
  

1.4.4 总结对比

谱型	适用场景	性能优势	局限性
Jakes	高速城市、密集多径	高动态适应性	不适用于低速或平坦地形
高斯	低速城市、丘陵地形	低频稳定性	高速场景性能下降
平坦	理论研究	计算简单	实际工程中失真严重

1.5 matlab代码

1.5.1 绘制多普勒功率谱

clc; clear; close all;

% 参数定义
f_max = 100;               % 最大多普勒频率 (Hz)
f = linspace(-f_max, f_max, 1000);  % 频率轴

% 计算Jakes功率谱，避免除0
S = zeros(size(f));
idx = abs(f) < f_max;  % 只对|f| < f_max有效

S(idx) = 1 ./ (pi * f_max * sqrt(1 - (f(idx)/f_max).^2));

% 绘图
figure('Color','w');
plot(f, S, 'LineWidth', 2);
xlabel('Frequency (Hz)');
ylabel('Power Spectral Density S(f)');
title('Jakes Doppler Power Spectrum');
grid on;
set(gca,'FontSize',12,'LineWidth',1.2);
axis tight;

仿真如下：

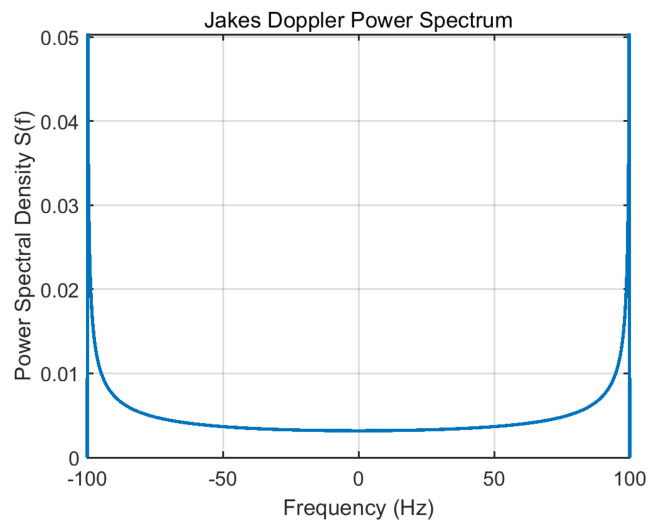
1.5.2 基于多径时延线性（TDL）模型和Jakes多普勒谱

clc; clear; close all;

%% 参数定义
fd = 100;              % 最大多普勒频移 (Hz)
fs = 1500;             % 采样率 (Hz)
duration = 1;          % 模拟时长 (秒)
N = fs * duration;     % 样本数
M = 32;                % Jakes 正弦波数量
L = 4;                 % 路径数 (TDL taps)
tau = [0, 1, 2.5, 5] * 1e-3;  % 各路径时延（秒）
pow_dB = [0 -3 -6 -9];        % 每条路径的功率（dB）
pow = 10.^(pow_dB/10);       % 转换为线性

%% 初始化信道矩阵
h_TDL = zeros(L, N);   % 每行表示一条路径的时变衰落 h_l(t)

%% 为每个tap生成瑞利过程
for l = 1:L
    h = jakes_strict(fd, fs, duration, M);  % 复高斯过程
    h_TDL(l, :) = sqrt(pow(l)) * h;         % 加权路径功率
end

%% 可视化：绘制每个tap的幅度变化
figure;
for l = 1:L
    subplot(L,1,l);
    plot((0:N-1)/fs, abs(h_TDL(l,:)));
    xlabel('Time (s)'); ylabel(['|h_' num2str(l) '(t)|']);
    title(['TDL Path ' num2str(l) ' Envelope']);
    grid on;
end
figure;
for l = 1:L
    % 计算第l条路径的PSD，使用pwelch函数
    [psd, f] = pwelch(h_TDL(l,:), hamming(256), 128, 512, fs, 'centered');
    
    % 绘制PSD（单位dB）
    plot(f, 10*log10(psd + 1e-12)); hold on;
end
grid on;
xlabel('Frequency (Hz)');
ylabel('Power Spectral Density (dB/Hz)');
title('PSD of Each TDL Path (Rayleigh Fading)');
legend(arrayfun(@(x) ['Path ' num2str(x)], 1:L, 'UniformOutput', false));

%% 子函数
function r = jakes_strict(fd, fs, duration, M)
    N = fs * duration;
    t = (0:N-1) / fs;
    n = 1:M;
    theta_n = pi * n / (M + 1);
    phi_n = 2 * pi * rand(1, M);
    omega_n = 2 * pi * fd * cos(theta_n);

    I = zeros(1, N);
    Q = zeros(1, N);
    for k = 1:M
        I = I + cos(phi_n(k)) * cos(omega_n(k) * t);
        Q = Q + sin(phi_n(k)) * cos(omega_n(k) * t);
    end

    r = sqrt(2/M) * (I + 1j * Q);  % 复信道系数
end

仿真如下：

1.5.2.1 代码讲解：

  上述代码严格遵循了Jakes模型的数学公式，通过分解复数形式的叠加为独立的同相（I）和正交（Q）分量来实现瑞利衰落信道的仿真。以下为具体对应关系及解释：

1. Jakes模型的原始公式

Jakes模型的复基带信道可表示为：
$$r(t)=\sqrt{\frac{2}{M}}\sum _{n=1}^M{e}^{j{\varphi }_n}\cos \left({\omega }_d\cos {\theta }_n\cdot t\right)$$
其中：

• ${\omega }_d=2\pi f_d$是最大多普勒角频率。
• ${\theta }_n$是第(n)个入射波的到达角，均匀分布在([0, \pi))。
• ${\varphi }_n$是随机初始相位，均匀分布在([0, 2\pi))。
• $M$是正弦波分量的个数。

2. 代码实现与公式的对应关系

代码中的循环部分：

for k = 1:M
    I = I + cos(phi_n(k)) * cos(omega_n(k) * t);  % 同相分量
    Q = Q + sin(phi_n(k)) * cos(omega_n(k) * t);  % 正交分量
end
r = sqrt(2/M) * (I + 1j * Q);                    % 归一化生成复信号

对应到Jakes公式的分解过程如下：

• 复数形式的分解
  Jakes公式中的复数指数项$e^{j{\varphi }_n}$可以分解为：
  $$e^{j{\varphi }_n}=\cos {\varphi }_n+j\sin {\varphi }_n$$
  因此，复基带信号可展开为：
  $$r(t)=\sqrt{\frac{2}{M}}\sum _{n=1}^M\left[\cos {\varphi }_n+j\sin {\varphi }_n\right]\cos ({\omega }_{n}t)$$
  其中，${\omega }_n={\omega }_d\cos {\theta }_n=2\pi f_d\cos {\theta }_n$（对应代码中的omega_n(k)）。

• 分离实部（I）和虚部（Q）：
  $$I(t)=\sum _{n=1}^M\cos {\varphi }_n\cdot \cos ({\omega }_{n}t)$$
  $$Q(t)=\sum _{n=1}^M\sin {\varphi }_n\cdot \cos ({\omega }_{n}t)$$

• 归一化因子**
  最终通过归一化确保信号功率为1：
  $$r(t)=\sqrt{\frac{2}{M}}\left(I(t)+jQ(t)\right)$$
  代码中的sqrt(2/M)与公式完全一致。

二、参考文献

[1] Singh, Swatantra Kumar and Ashish Xavier Das. “Channel modeling for Urban and Hilly terrain using Jakes, Gaussian and Flat spectrum for Ad-hoc network.” (2015).