最长回文子串(Longest Palindromic Substring)

题目

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1：
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：
输入: “cbbd”
输出: “bb”

解析

子串（substring）:原始字符串的一个连续子集；
子序列（subsequence）:原始字符串的一个子集；
区别：子串连续，子序列不必连续

一般处理：

• 先计算出子串的长度，如果长度小于2，则直接将原字符串返回；
• 用maxlen记录当前最长子串长度，用begin记录最长子串的起始位置；
• 然后可以将字符串转换为字符数组，方便对数组每一位进行处理和提取；

方法一：暴力枚举

用两层循环，原则上枚举所有长度严格大于1的子串charArray[i…j]，然后用从两端缩到中间的方法，来判断对称的每两个字符是否相等，来暴力枚举一串字符中的每个字符是否符合回文子串的规则；

C++代码：

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;
//验证是否回文
bool valid(string s, int left, int right) {
 // 验证子串 s[left, right] 是否为回文串
 while (left < right) {
  if (s[left] != s[right]) {
   return false;
  }
  left++;
  right--;
 }
 return true;
}
//暴力枚举法
string longestPalindrome_BruteForce(string s) {
 // 特判
 int size = s.size();
 if (size < 2) {
  return s;
 }
 int begin = 0;
 int maxLen = 1;
 string res = s.substr(0, 1);
// 枚举所有长度大于等于 2 的子串
 for (int i = 0; i < size - 1; i++) {
  for (int j = i + 1; j < size; j++) {
   if (j - i + 1 > maxLen && valid(s, i, j)) {
    begin = i;
    maxLen = j - i + 1;
    
   }
  }
 }
 res = s.substr(begin, maxLen);
 return res;
}

时间复杂度：O(N³)，这里 N 是字符串的长度，枚举字符串的左边界、右边界，然后继续验证子串是否是回文子串，这三种操作都与 N 相关；
空间复杂度：O(1)，只使用到常数个临时变量，与字符串长度无关。

方法二：动态规划

对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串“ababa”，如果我们已经知道 “bab” 是回文串，那么 “ababa” 一定是回文串，这是因为它的首尾两个字母都是 “a”。

状态：用dp[i][j]来表示子串s[i…j]是否是回文子串；
状态转移方程：dp[i][j] = （s[i]==s[j]）&&dp[i+1][j-1]，表示dp[i][j]的状态由边界值是否相等和去掉了头部的子串的回文情况决定；即：dp[i][j] = （s[i]==s[j]）&&（j-i<3 || dp[i+1][j-1]）
边界条件：j-1-（i+1）<2,整理得：j-i<3，
语义：当子串s[i…j]长度为2或3时，不用检测子串是否是回文串；初始化：二维表格dp[][],dp[i][j]=True;
输出：当发现一个回文子串时，即dp[i][j]为true时，记录起始位置和回文长度，进行填表。

每一个状态dp[i][j]的值都受左下方值的影响，对角线的值不会被参考（自己计算下，会发现的），计算填表只计算j>i的部分，由于需要参考左下方的值，因此填表顺序参考：依顺序按列填写，每一列从第0行开始算起。
C++代码：

//动态规划
string longestPalindrome(string s) {
 int len = s.size();
 if (len < 2)
 {
  return s;
 }
 vector<vector<int>> dp(len, vector<int>(len));
 for (int i = 0; i < len; i++)
 {
  dp[i][i] = 1;
 }
 string ans;
 int maxlen = 1, begin = 0;
 for (int j = 1; j < len; ++j) {
  for (int i = 0; i  < j ; ++i) {
   dp[i][j] = (s[i] == s[j] && ((j - i) < 3 || dp[i + 1][j - 1]));
   //以下判断部分可被如上简短判别式替换
   //if (s[i] != s[j])
   //{
   // dp[i][j] = 0;
   //}
   //else
   //{
   // if (j - i < 3)//s[i...j]的长度为2或者3
   // {
   //  dp[i][j] = 1;
   // }
   // else
   // {
   //  dp[i][j] = dp[i + 1][j - 1];
   // }
   //}
   //更新状态
   if (dp[i][j] && ((j - i + 1)>maxlen))
   {
    maxlen = j - i + 1;
    begin = i;
   }
  }
 }
 ans = s.substr(begin, maxlen);
 return ans;
}

其实我们可以发现动态规划也是两层循环，只是在暴力枚举的基础上加了一个二维数组，用于统计先前子串的回文状态，也就是典型的空间换时间。
时间复杂度：O(n²)，其中 n 是字符串的长度。动态规划的状态总数为 O(n²)，对于每个状态，我们需要转移的时间为 O(1)。
空间复杂度：O(n²)，即存储动态规划状态需要的空间。

方法三：马拉车算法（Manacher）

在介绍Manacher之前，先介绍一下中心扩展算法，中心扩展算法类似暴力枚举，但是是和暴力枚举相反，暴力枚举是枚举每一个s[i]和s[j]，若不等，则s[i…j]不是回文子序列，如果s[i]和s[j]相等，则从两端向中间缩减，继而判断s[i+1]和s[j-1]是否相等，如此继续下去，而中心扩展算法是先判断s[i]和s[j]是否相等，若不等，则s[i…j]不是回文子序列，若相等则判断s[i-1]和s[j+1]的关系，因此中心扩展和暴力枚举的方向是相反的。

而Manacher是利用了中心扩展方法，但不仅仅是中心扩展，不然和暴力枚举的时间复杂度没有多改善。

Manacher算法先将字符串预处理，在每个字符间加一个和字符串中字符完全无关的字符来做分割，在头尾都加一个可以识别边界标识符，如下（经常这样的预处理，无论原来的字符串长度是奇数还是偶数，最后都是奇数长度”不包含开始的头部标识符$”，方便回文判断）：
bob --> #b#o#b#
noon --> $#n#o#o#n#

再比如：

可以看到原字符串和处理后字符串的关系。

Manacher算法是在枚举每个i位置元素时，都把之前最长回文子串的“臂长”、“回文中心”都作为i位置回文子串判断的依据，如下图，i为当前循环变量的索引，center为之前的最长回文子串的中心，maxright为其最右边界，mirror是i关于center的对称索引，mirror = 2*center - i ；

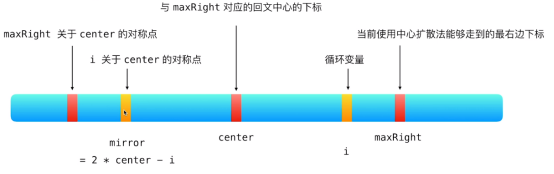
在Manacher算法中，i位置元素的回文序列判断会利用到关于center对称的mirror的回文子序列，p[i]是对应以s[i]为回文中心的回文半径，具体判断如下：
1）当i<maxright时，分为三种情况：
①p[mirror]<maxright - i,p[i] = p[mirror];

②p[mirror]=maxright - i,p[i]至少为maxright - i，具体需要从maxright向外扩展;

③p[mirror]>maxright - i,p[i]最多为maxright - i，不可能索引为maxright+1的元素和2*center -maxright-1的元素相等，相等的话，center中心的回文半径至少为maxright+1了。
总结得：当i<maxright时,p[i]= min (p[mirror],maxright -i),然后尝试中心扩散。

2）当i>=maxright时，具体需要从maxright向外扩展；
C++代码：

string Manacher1(string s) 
{
 // Insert '#'
 string t = "$#";
 for (int i = 0; i < s.size(); ++i) {
  t += s[i];
  t += "#";
  }
 // Process t
 vector<int> p(t.size(), 0);
 int mixright = 0, center = 0, maxlen = 0, begin = 0;
 for (int i = 1; i < t.size(); ++i) {
 	p[i] = mixright > i ? min(p[2 * center - i], mixright - i) : 1;
  	while (t[i + p[i]] == t[i - p[i]]) 
   		++p[i];
   	if (mixright < i + p[i]) {
   		mixright = i + p[i];
   		center = i;
  	}
  	if (maxlen < p[i]) {
   		maxlen = p[i];
   		begin = i;
  	}
  }
  return s.substr((begin - maxlen) / 2, maxlen - 1);
}

时间复杂度：O(N)，Manacher 算法只有在遇到还未匹配的位置时才进行匹配，已经匹配过的位置不再匹配，因此对于字符串 S 的每一个位置，都只进行一次匹配，算法的复杂度为 O(N)。
空间复杂度：O(N)。

方法四：最长公共子串

可以将最长回文子串问题转换成最长公共子串的方法，那就是将原字符串S反转，使之变成S’ 。找到S和S’之间最长的公共子串，这也必然是最长的回文子串。

这似乎是可行的，让我们看看下面的一些例子。
例如：S=“abcbd”,S’=“dbcba”,可以得到S和S’的在最长公共子串是“bcb”。

在看另外一个例子，S = “abcdfgdcba”，S’ =“abcdgfabcd”，可以得到S和S’的最长公共子串是“abcd”，显然，这不是回文。

我们可以看到，当S的其他部分中存在非回文子串的反向副本时，最长公共子串法就会失败。为了纠正这一点，每当我们找到最长的公共子串的候选项时，都需要检查子串的索引是否与反向子串的原始索引相同。如果相同，那么我们尝试更新目前为止找到的最长回文子串；如果不是，我们就跳过这个候选项并继续寻找下一个候选。

这是一个时间复杂度为O（n²）的动态规划算法，空间复杂度也为O（n²）。下面举个例子：

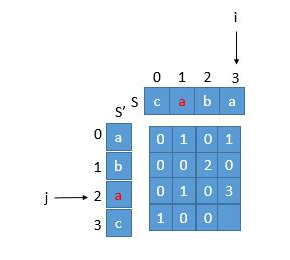
看图就知道S’是S字符串的倒置，我们只要通过两层循环，判断S[i]和S[j]是否相等，如果相等，则二维数组S[i][j] = S[i-1][j-1] + 1，你仔细想一下就知道为什么了，你看图会发现S[i][j]和S[i-1][j-1]的关系，这样S[i][j]里面记录的就是这两个相等子串的长度，也就是找到公共子串的算法，那接下来我们怎么判断是否是回文呢？正如上边所有直接反转字符进行最长公共子串判断，并不行，还需要判断该字符串倒置前的下标和当前的字符串下标是不是匹配。例如S="abc435cba"和S’的最长公共子串是 "abc"和 “cba”，但很明显这两个字符串都不是回文串，还需要所以我们求出最长公共子串后，并不一定是回文串，我们还需要判断该字符串倒置前的下标和当前的字符串下标是不是匹配。当然我们不需要每个字符都判断，我们只需要判断末尾字符就可以。是不是很简单，那就直接上代码。时间复杂度是O(n^2)哦。当然啦，可以使用动态规划，将这个空间复杂度降低一个level.

JAVA代码：

    public static String longestPalindromeS3(String s) {
        if(s.equals(""))
            return "";
        String origin = s;
        String reverse = new StringBuilder(s).reverse().toString();
        int length = s.length();
        int[][] arr = new int[length][length];
        int maxLen = 0;
        int maxEnd = 0;
        for(int i = 0; i < length; i++)
            for(int j = 0; j < length; j++){
                if(origin.charAt(i) == reverse.charAt(j)){
                    if(i == 0 || j == 0){
                        arr[i][j] = 1;
                    }else{
                        arr[i][j] = arr[i - 1][j - 1] + 1;
                    }
                }
                if(arr[i][j] >  maxLen){
                    int beforeRev = length - 1 - j;
                    if(beforeRev + arr[i][j] - 1 == i){ // 用于判断下标是否对应，从而判断是否是回文
                        maxLen = arr[i][j];
                        maxEnd = i;
                    }
                }
            }
            return s.substring(maxEnd - maxLen + 1, maxLen + 1);
    }

总结一下博客，因为天太热，电脑自动关机了10多次，崩溃o(╥﹏╥)o

参考

1、https://zhuanlan.zhihu.com/p/38251499
2、https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode-solution/
3、link
4、https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/