BFV同态加密方案初步学习

BFV是把Bra12的LWE版本推到了RLWE版本，Bra12也可以叫做BFV。

经典的RLWE的公钥加密算法回顾

对比以前的Regev的LWE公钥加密方案，其实几乎只是把明文空间换了，也就是在最大比特编码的时候把2换成t，即，$\Delta =\lfloor q/t\rfloor$。同时这里的$q$是没有限制的，也就是可以使用2的幂次来简化运算。

这里可以这样看$\mathbf{s}=(1,\mathbf{s})$,$\mathbf{c}\mathbf{t}=({\mathbf{c}}_0,{\mathbf{c}}_1)$。
对于正确性验证
$\begin{array}{rl}{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}& ={\mathbf{p}}_0\cdot \mathbf{u}+{\mathbf{e}}_1+\Delta \cdot \mathbf{m}+{\mathbf{p}}_1\cdot \mathbf{u}+{\mathbf{e}}_2\\ & =-\mathbf{a}\cdot \mathbf{s}\cdot \mathbf{u}+\mathbf{e}\cdot \mathbf{u}+{\mathbf{e}}_1+\Delta \cdot \mathbf{m}+\mathbf{a}\cdot \mathbf{s}\cdot \mathbf{u}+{\mathbf{e}}_2\cdot \mathbf{s}\\ & =\Delta \cdot \mathbf{m}+\mathbf{e}\cdot \mathbf{u}+{\mathbf{e}}_1+{\mathbf{e}}_2\cdot \mathbf{s}(\mathrm{m}\mathrm{o}\mathrm{d}q)\end{array}$
可以看到这里的噪声似乎与$\mathbf{u}$和$\mathbf{s}$有关，如果将这两个取的小一点，能够一定程度上减低噪声。
另外，将噪声用$\mathbf{v}=\mathbf{e}\cdot \mathbf{u}+{\mathbf{e}}_1+{\mathbf{e}}_2\cdot \mathbf{s}$表示，能够得到$[{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}{]}_q=\Delta \cdot \mathbf{m}+\mathbf{v}$，与此同时若取样的$\chi \le B$的话，我们将得到噪声的界限，即$\mathbf{v}\le 2\cdot B^2\cdot {\delta }_R+B$，其中${\delta }_R$表示扩张因子
${\delta }_R=\max \left\{\frac{\Vert a\cdot b\Vert }{\Vert a\Vert \cdot \Vert b\Vert }:a,b\in R\right\}$，其中的$||a||=ma{x}_i|a_i|$为无穷范数。

同态方案

方案是基于前面的LPR.ES方案的，作为优化，该方案增加了一个重线性化，将$\mathbf{u}$和$\mathbf{s}$的取值范围变为${\mathbb{R}}_2$，即它们的范数为1，其他基本一致
借用BV11里面的思想，将解密过程看作一个解密函数，即得到，
$[\mathbf{c}\mathbf{t}(\mathbf{x}){]}_q=[{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{x}{]}_q$
代入密钥就能得到明文
$[\mathbf{c}\mathbf{t}(\mathbf{s}){]}_q=\Delta \cdot \mathbf{m}+\mathbf{v}$

同态乘法

来看看核心的乘法运算

该定理表明，乘法时，噪声不是呈平方增长，而是大致上乘以了一个系数$2\cdot t\cdot {\delta }_R^2\cdot ||\mathbf{s}||$，也就是线性增长，从表达式里能看到，对噪声有显著影响的是$t$和$\mathbf{s}$的范数。（具体引理证明感兴趣可以去原文看看😇）

重线性化

然后用BV11中的函数思想，两个函数相乘得到的将是三项，成为二次函数，需要执行重线性化让它还原为两项也就是一次式。
假设一个二阶的密文为$[{\mathbf{c}}_0,{\mathbf{c}}_1,{\mathbf{c}}_2]$，线性化的目的是将它变成一阶的$[{\mathbf{c}}_0^{\prime },{\mathbf{c}}_1^{\prime }]$即${\left[{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}+{\mathbf{c}}_2\cdot {\mathbf{s}}^2\right]}_q={\left[{\mathbf{c}}_0^{\prime }+{\mathbf{c}}_1^{\prime }\cdot \mathbf{s}+\mathbf{r}\right]}_q$，其中$\mathbf{r}$很小。
由于${\mathbf{s}}^2$是不可知的，所以这里选用的方式是加密一手。
为此，这里引入了一个重线性化密钥$rlk=([-({\mathbf{a}}_0\cdot \mathbf{s}+{\mathbf{e}}_0)+{\mathbf{s}}^2{]}_q,{\mathbf{a}}_0)$,满足$rlk[0]+rlk[1]\cdot \mathbf{s}={\mathbf{s}}^2+{\mathbf{e}}_0$

方案一（T进制分解）

第一种使用$rlk$来转换密文的方法是令${\mathbf{c}}_0^{\prime }={\mathbf{c}}_0+rlk[0]\cdot {\mathbf{c}}_2$和${\mathbf{c}}_1^{\prime }={\mathbf{c}}_1+rlk[1]\cdot {\mathbf{c}}_2$这样得到的噪声$\mathbf{r}={\mathbf{e}}_0\cdot {\mathbf{c}}_2$（独立于密文的噪声，只是重线性化带来的噪声），但是由于${\mathbf{c}}_2\in R_q$,直接使用的话，会导致噪声被放大很多很多，所以需要进行分解。
那么这里的方法是选择一个基（独立于$t$），将${\mathbf{c}}_2$切片。即令
${\mathbf{c}}_2={\sum }_{i=0}^{\ell }{T}^i\cdot {\mathbf{c}}_2^{(i)}$,其中$\ell =\lfloor {\log }_T(q)\rfloor$,且${\mathbf{c}}_2^{(i)}$系数均在$R_T$中，与此对应的设置重线性化密钥为$rlk=\left[\left({\left[-\left({\mathbf{a}}_i\cdot \mathbf{s}+{\mathbf{e}}_i\right)+T^i\cdot {\mathbf{s}}^2\right]}_q,{\mathbf{a}}_i\right):i\in [0..\ell ]\right]$
由此得到更新后的密文为
${\mathbf{c}}_0^{\prime }={\left[{\mathbf{c}}_0+{\sum }_{i=0}^{\ell }\mathrm{rlk}[i][0]\cdot {\mathbf{c}}_2^{(i)}\right]}_q\text{ and }{\mathbf{c}}_1^{\prime }={\left[{\mathbf{c}}_1+{\sum }_{i=0}^{\ell }\mathrm{rlk}[i][1]\cdot {\mathbf{c}}_2^{(i)}\right]}_q$
最终得到的噪声将为$\mathbf{r}={\sum }_{i=0}^{\ell }{\mathbf{c}}_2^{(i)}\cdot {\mathbf{e}}_i$。
这样操作的结果是$T$越大，$rlk$越小，噪声$\mathbf{r}$就越大，但是$T$越小，$rlk$就会越大，那么计算速度就会变慢。同时由于重线性化的噪声独立于密文噪声，为了良好的同态，应该让噪声$\mathbf{r}$的值在密文噪声的附近。
动态线性化：先选取足够小的$T$来获取足够小的误差，当几次乘法导致误差变大后，可以选择对$T^2$进行线性化进行加速，也就是计算包含$T^2$的$rlk$，由此$rlk$中应当包含所需的所有信息。（有点懵还，原文是这么写的）

方案二（模切换）

先给出一个能大模数的能够容纳较大误差噪声的加密版本的${\mathbf{s}}^2$，然后再进行缩放来获取所需要的。
更新$rlk=(-[(\mathbf{a}\cdot \mathbf{s}+\mathbf{e})+p\cdot {\mathbf{s}}^2{]}_{p\cdot q},\mathbf{a})$，其中$a\in R_{p\cdot q}$和$\mathbf{e}\leftarrow {\chi }^{\prime }$（和前面是不一样的分布）。同时密文也要更新为，
${\mathbf{c}}_0^{\prime \prime }={\left[\lfloor \frac{{\mathbf{c}}_2\cdot \mathbf{r}\mathbf{l}\mathbf{k}[0]}{p}\rfloor \right]}_q$,${\mathbf{c}}_1^{\prime \prime }={\left[\lfloor \frac{{\mathbf{c}}_2\cdot \mathbf{r}\mathbf{l}\mathbf{k}[1]}{p}\rfloor \right]}_q$
简单计算能得到${\mathbf{c}}_0^{\prime \prime }+{\mathbf{c}}_1^{\prime \prime }\cdot s={\mathbf{c}}_2^{\prime \prime }\cdot {\mathbf{s}}^2+\mathbf{r}$
粗略的估算能得到$\Vert \mathbf{r}\Vert <\frac{q\cdot B_k\cdot {\delta }_R}{p}+\left({\delta }_R\cdot \Vert s\Vert +1\right)/2$
动态线性化：选择足够大的$p$来获取足够小的误差，多次乘法噪声增大后就可以通过提取$p^{\prime }/p$，切换模数，来形成有效$rlk$进行加速。

同态方案

这里方案和前面的LPR方案很类似，不同的是，$\mathbf{s}$和$\mathbf{u}$的取值范围是$R^2$（这是为了减小噪声），多了重线性化密钥（缩减密文规模的）。
密文的形式是$\mathbf{c}t=({\mathbf{c}}_0,{\mathbf{c}}_1)$，乘法其实就是两个密文对应项的乘，然后类似Bra12中的一样乘以一个缩放系数$t/q$用于减小噪声
然后是重线性化，和之前描述的一样

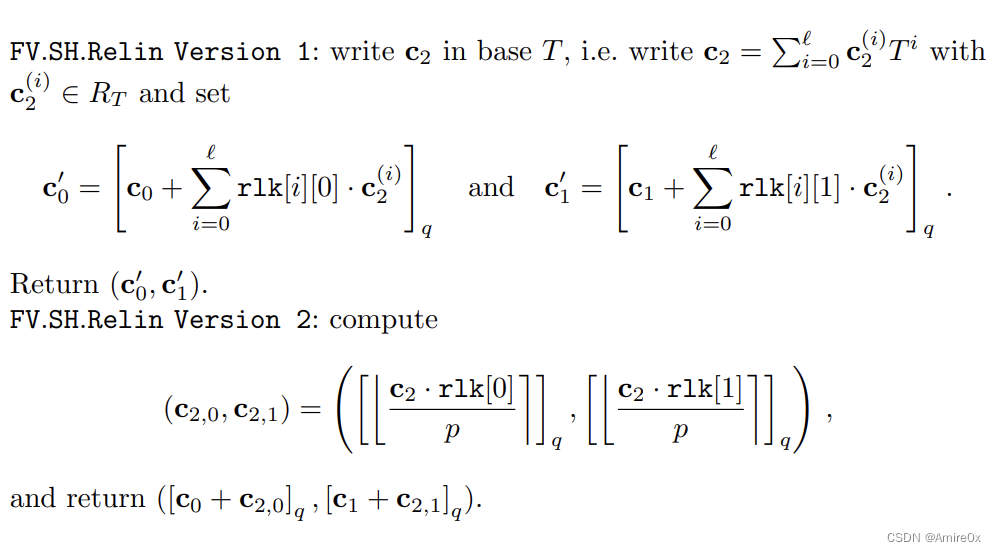
要实现乘法深度为$L$的电路，需要满足
$4\cdot {\delta }_R^L\cdot {\left({\delta }_R+1.25\right)}^{L+1}\cdot t^{L-1}<\lfloor q/B\rfloor$

全同态方案

（这块儿有点迷糊，没咋看懂，后面有需要再补吧）
采用的是Gentry的Bootstrapping方法，即在噪声达到最大值之前，进行一次同态解密，使得密文具有固定的噪声，且之后仍能进行一次乘法运算。
同态解密的条件是解密电路的深度必须小于同态运算最大深度，由此，需要对上面方案的解密方案进行处理。
这里采用的是不允许解密运算中的噪声$\mathbf{v}$增长到界限，而是将它限制在$\Delta /\mu (\mu >2)$内，可以通过将低位全部设置为0来忽略$\mathbf{c}t[0]$和$\mathbf{c}t[1]$中的大部分，从而达到优化解密的目的。
设置后，会增加一部分误差，即，把$\mathbf{c}t[0]$和$\mathbf{c}t[1]$，替换为了${\mathbf{c}}_0=\mathbf{c}t[0]+{\mathbf{e}}_0$和${\mathbf{c}}_1=\mathbf{c}t[1]+{\mathbf{e}}_1$（$||{\mathbf{e}}_i||<\Delta /v$）。
这样将得到一个增加了新噪声的密文${\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}=\Delta \cdot \mathbf{m}+\mathbf{v}+{\mathbf{e}}_0+{\mathbf{e}}_1\cdot \mathbf{s}+q\cdot \mathbf{r}$
为了约束新增加的噪声，这里定义了两个函数$\mathrm{abs}(a(x))\in Z[x]$为将系数绝对值化后的多项式，并定义函数
$H(f)=\max \left\{\Vert {\sum }_{i=0}^{d-1}\mathrm{abs}\left(x^{i+j}\mathrm{m}\mathrm{o}\mathrm{d}f(x)\right)\Vert \mid j=0,\dots ,d-1\right\}$
对于分圆多项式如$f=x^d+1$，代入上面函数能得到$H(f)=1$,用$h$代表$\mathbf{s}$的汉明距离（比特中的非0个数），会得到噪声的界限是$\Delta /\mu +(H(f)\cdot h+1)\cdot \Delta /\nu$，当满足条件$2\cdot \mu \cdot (H(f)\cdot h+1)<\nu \cdot (\mu -2)$时，密文能够正确解密。

参考

Fan, Junfeng and Frederik Vercauteren. “Somewhat Practical Fully Homomorphic Encryption.” IACR Cryptol. ePrint Arch. 2012 (2012): 144.
全同态加密BFV-(section 1-基础知识)
全同态加密BFV-(section 2-SHE)
全同态加密：BFV