参考链接:https://oi-wiki.org/math/mobius/#_2
莫比乌斯反演:对于一些函数 f(x),如果很难直接求出它的值,而容易求出其倍数和或约数和 g(x) ,那么可以通过莫比乌斯反演简化运算,求得 f(x) 的值。
开始学习莫比乌斯反演前,我们需要一些前置知识:数论分块与整数项、积性函数 、 Dirichlet 卷积 、 莫比乌斯函数。
数论分块与整数项:
引理1:
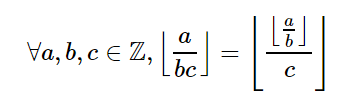
证明:
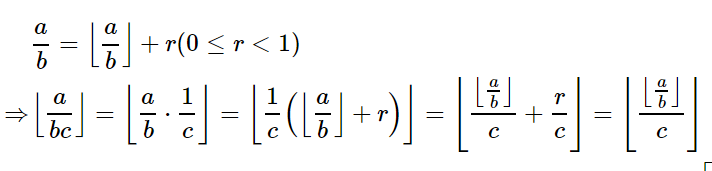
引理2:
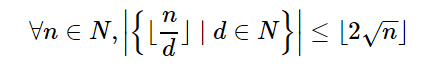
证明:
对于![]() ,
,![]() 有
有![]() 种取值。
种取值。
对于![]() ,有
,有![]() ,也只有
,也只有![]() 种取值。
种取值。
数论分块:
考虑含有![]() 求和的式子,对于任意一个i(i<=n),我们需要找到一个最大的j(i<j<n),使得
求和的式子,对于任意一个i(i<=n),我们需要找到一个最大的j(i<j<n),使得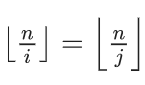 。
。
而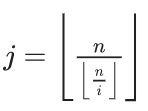 。
。
证明:

利用上述结论,我们每次分[i,j]为一块,分块求和即可。
代码实现:
for(int i = 1, j; i <= n;i = j+1)
{
j = n / (n / i);
ans += (j-i+1)*(n/i+n/i)/2;//一块求,前面为等差数列求和公式
printf("%d %d\n", i, j);
}积性函数:
定义:
对于所有互质( gcd( a,b ) =1)的整数 a 和 b ,有性质 f ( ab ) = f( a )f( b )。
性质:
若 f( x ) 和 g( x )均是积性函数,那么以下函数h( x )也是积性函数:

积性函数举例(即以下函数都是积性函数,都可以利用积性函数的性质):
- ——摘自百度百科
φ(n) -欧拉函数
μ(n) -莫比乌斯函数(关于非平方数的质因子数目)
gcd(n,k) -最大公因子,当k固定的情况
d(n) -n的正因子数目
σ(n) -n的所有正因子之和
σk(n) - 因子函数,n的所有正因子的k次幂之和,当中k可为任何复数。
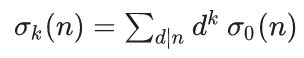
1(n) -常数函数,定义为 1(n) = 1 (完全积性)
Id(n) -单位函数,定义为 Id(n) = n(完全积性)
Idk(n) -幂函数,对于任何复数、实数k,定义为Idk(n) = n^k (完全积性)
λ(n) -刘维尔函数,关于能整除n的质因子的数目
Dirichlet卷积:
更为详尽的博客:
定义:
定义数论函数 f 和 g 的迪利克雷卷积为h(x),则 h( x ) = ( f * g )( n )
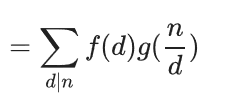
性质:
迪利克雷卷积满足结合律和交换率,对加法满足交换率。
其中单位元为ϵ,ϵ(n)=[n=1]。
常见的迪利克雷卷积:

莫比乌斯函数:
学习了狄利克雷卷积后,我们来看以下几个常见的积性函数:
- 常函数:I(n)=1
- 单位元为ϵ,ϵ(n)=[n=1](即只有当n等于1时,ϵ(1)=1,其余情况都为0)
- ϵ∗f=f
- 已知函数f,定义函数f的逆f^−1,满足f∗f^−1=ϵ,且积性函数的逆也是积性函数
- 由上一条可得f^−1(1)=1/f(1)
莫比乌斯函数就是一个积性函数,并且含有以下的性质:

证明:
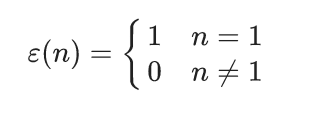
其中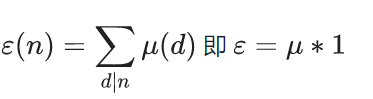
设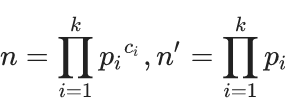
那么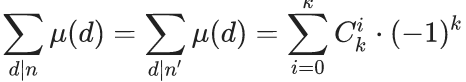
根据二项式定理,该公式在k=0或者n=1时为1,否则为0。
反演推论: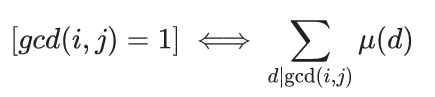
线性筛
由于μ是积性函数,所以可以线性的筛莫比乌斯函数(线性筛可以求所有的积性函数,但是方法不相同)。
int miu[10000];
void Miu() {
miu[1] = 1;
for (int i = 2; i <= n; ++i)
{
if (!flg[i])
{
p[++tot] = i;
miu[i] = -1;
}
for (int j = 1; j <= tot && i * p[j] <= n; ++j)
{
flg[i*p[j]]=1;
if (i%p[j]==0)
{
miu[i*p[j]]=0;
break;
}
miu[i*p[j]]=-miu[i];
}
}
}莫比乌斯反演
设f(n)、g(n)为两个莫比乌斯函数。
如果有
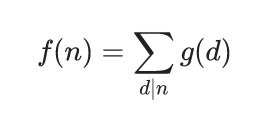
那么
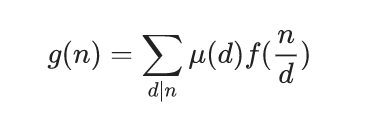
证明:
原命题为,已知![]() ,证明
,证明![]()
易知如下转化:![]()






















 119
119











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








