牛客算法周周练1 A Maximize The Beautiful Value

题目描述

Today HH finds a non-decreasing sequence(a ₁,a ₂....a _n,a _i≤a _i+1), he thinks it's not beautiful so he wants to make it beautiful.

To make it, HH will choose exactly one number and move it forward at least k steps(i.e. you can move a _i to a _j if k≤i−j), and then he defines the beautiful value F(n) as 

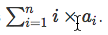
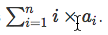
HH asks you to calculate max(F(n))

输入描述:

  
  

   
    The first line contains an positive integer T(1≤T≤10), represents there are T test cases. 
  
  
  
  

   
    For each test case: 
  
  
  
  

   
    The first line contains two positive integers n,k(1≤n≤10
   
   5,1≤k<n)，the length of the sequence ,the least steps you need to move. 
  
  
  
  

   
    The second line contains n integers a
   
   1,a
   
   2…a
   
   n(1≤a
   
   i≤10
   
   8) - the sequence.
  
  

输出描述:

For each test case, you should output the max F(n).

示例1

输入

复制 3 5 3 1 1 3 4 5 5 2 1 1 3 4 5 5 1 1 1 3 4 5

3
5 3
1 1 3 4 5
5 2
1 1 3 4 5
5 1
1 1 3 4 5

输出

复制 46 50 53

46
50
53

说明

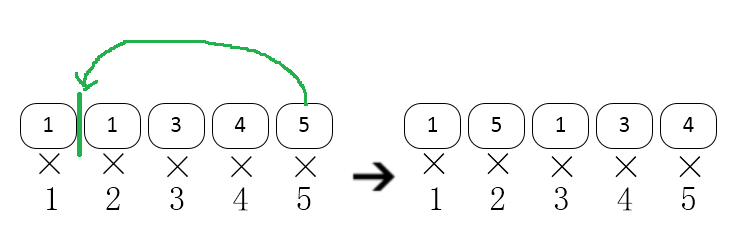
In the first example, you can move the fifth number 4 for 3 steps and make the sequence become [4,1,1,3,5], then the beautiful value is 4×1+1×2+1×3+3×4+5×5=46.
You can also move the fifth number to make it become [1,5,1,3,4], the beautiful value is also 46.
In the second example, you can move the  fifth number 5 for 2 steps and make the sequence become [1,1,5,3,4]
In the second example, you can move the  second number 1 for 1 steps and then the sequence is still [1,1,3,4,5]

备注:

scanf is commended。

思路

1. 首先定义一个初始和sum=a[i]i+a[i+1](i+1)....(i=1~n)
2. 答案可以由初始的sum减去一个值M得到
3. 通过模拟发现这个值为M=a[i]k-(a[i-k]+a[i-k+1]+...+a[i-1])，共k个数*
4. 使用前缀和、枚举模拟找最小的M

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#define ll long long 
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
	int n,k;
	cin>>n>>k;
	vector<ll> arr(n+1,0);
	vector<ll> sum(n+1,0);
	ll ans=0;
	for(int i=1;i<=n;i++)
	{
		cin>>arr[i];
		ans+=(i*arr[i]);
		sum[i]=sum[i-1]+arr[i];
	}
	ll mi=1e13;   //开大点不然WA
	for(int i=n;i>=k+1;i--)
	{
	    ll s=arr[i]*k-(sum[i-1]-sum[i-1-k]);   //移动产生的差值

		mi=min(mi,s);	
	}
	cout<<ans-mi<<endl;
}
	return 0;
}