图像分割算法——Normalized Cuts（Ncuts）算法的简单理解

LinKouun

已于 2023-02-12 05:32:07 修改

阅读量9.8k

点赞数 35

文章标签：算法

于 2021-12-29 20:46:10 首次发布

本文链接：https://blog.csdn.net/qq_43349296/article/details/122222469

版权

这篇博客介绍了基于图论的图像分割方法，特别是Normalized Cuts（Ncuts）算法，如何通过转化成图的最小割问题来确定图像区域。作者详细阐述了最小割的概念，以及为何这种方法能有效分割图像，同时讨论了如何改进目标函数以避免孤立像素的分割问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最近在做毕业设计，看文献综述时查了一些资料，打算在CSDN上对现有的图像分割方法做一些简单的笔记：

首先需要介绍的是，该算法是一种基于图论的算法：将整幅图像映射为一个带权值的无向图G=(V, E)，V为点集，E为边集。图像中的像素点视为图中的顶点，像素点之间相邻关系表示为图中的边，像素点间的相似性或差异性为边的权值。基于图论的算法主要思想是：将图像分割问题，转化为图论中图的划分问题，从而求解。

下面具体说一说Normalized Cuts算法（Ncuts）。该算法的创作者Wu等人根据图论当中的最小割（min-cut）的定义，将图像分割问题转化为求解对应图的最小割问题。

什么是最小割问题？首先明确什么是割：对于一张无向带权图G = (V, E, w)，若存在边集C，将点集V分为点集S和点集T，满足S∪T = V，S∩T = ∅，C中任何一条边的两个端点分别属于S和T中，那么称C = (S, T)是图G的一个割（也称作割集）。最小割指的就是边权值之和最小的割集，最小割问题就是要求解最小割。

在图像分割问题中，定义最小割问题的目标函数可以这样表示：

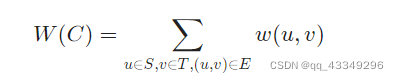
图1

其中𝑤(u,v )为(u,v )边的权值。求解最小割的方法大家可以参考这篇文章：https://riteme.site/blog/2017-2-12/mincut.html。本文只是对Ncuts算法做简单理解和笔记，并不详细描述算法的具体实现。

那么为什么我们可以将图像分割问题转化为最小割问题求解呢？我是这么理解的，举个例子：图像分割问题就是根据像素点之间的相似程度来确定不同的区域，从而分割图像，则定义相邻像素点之间的相似程度为边，相似程度越大，边的权值越大。而且很显而易见的一点是：不同区域之间的差异是非常大的，因此相邻区域之间连通的边的权值，一定都是较小的值（不同区域之间相似程度小，相邻边的权值就很小）。所以我们可以这样想：找到了权值之和比较小的边集，就可能相当于找到了区域的边界。可利用下图来做解释：

图2

在图2中，黄色拼图区域中的像素点之间，边权值一定是非常大的（因此这些权值很大的边不可能存在于最小割集中），而不同区域之间的边权值肯定很小，比如黄色拼图区域与蓝色拼图区域边界线上的边权值，一定是很小的值，这就是为什么我们需要求最小割集来解决图像分割问题。

但是仅用上文提到的目标函数来做图像分割时, 往往会出现分割单个点的情况，如下图所示：

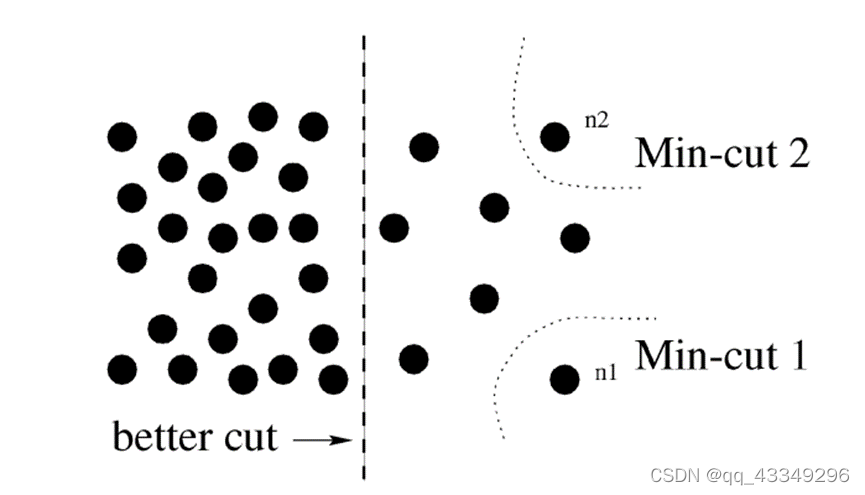
图3

注：该图引用自原Ncuts算法论文原文

可以看到，普通的最小割算法会更加倾向于做Min-cut1和Min-cut2这样的分割，因为单个像素点所组成的点集，与其他点集相邻的边一般是最少的，所以边权值之和往往也是最小的，这样一来，结果往往是分割出了一个个孤立的像素点，实验结果并不理想。我们真正想要的图像分割，实际上是类似图中better cut这样的。

为了解决上文所提到的问题，Wu等人改进了目标函数，变成了下图这个样子：