二分图的匹配问题以及求解算法

概念

二分图：二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V被分割为两个互不相交的顶点子集(A,B)，并且边集E中的每条边（vi，vj）所关联的两个顶点vi和vj分别属于这两个不同的顶点集(比如vi in A,vj in B或者vi in B,vj in A)，则称图G为一个二分图。

举例如下：

我们发现，A内部的顶点之间是没有边的，B也是，只有A,B相互之间连接，这就是二分图。

问题定义

在介绍二分图的匹配问题之前，先看个直观的例子。
把上面给的这幅图想象成结婚问题，其中B代表男生，A代表女生。连线表示这个男生的心动女生（可能有多个）。现在问存不存在一种方案使得B中的所有男生都能够和自己的心动女生结婚？如果不存在，那么B中最多可以有几个男生和他们的心动女生结婚？

在上述的二分图中，是可以的，如下面的箭头所示，每一个B中的男生都找到了自己的配偶。

下面正式引出一般性地二分图的匹配问题，

二分图的匹配问题：给定一个二分图，问最大匹配是多少？

例如，上面这个二分图的最大匹配是4。

其他概念：

1. 匹配：匹配是边的集合，在该集合中，任意两条边不能有共同的顶点。否则岂不是一个人同时结两个婚。
2. 完美匹配：完美匹配是集合A和集合B的双射。上述例子中不存在完美匹配，因为女生多了一个，最多只有4对鸳鸯，注定有一个女生要寂寞空虚冷。

我们可以发现：完美匹配一定是最大匹配，但是最大匹配不一定是完美匹配。上面的例子就说明了这么一点。

那我们的算法要求解最大匹配还是求完美匹配？当然是最大匹配，因为最大匹配总是存在的，而完美匹配不一定存在。另外，求得了最大匹配，再来判断这个最大匹配是不是完美匹配太简单了，看是不是所有人都结婚了即可。

求解算法-匈牙利算法

匈牙利算法的英文名称是：Hungary，也是匈牙利国家的名字，太逗了。
我们给个例子，跟着匈牙利算法走一遍流程就什么都懂了。给定一个二部图如下：

我们以上面的$x$为基准，从左边开始依次找配对，所以我们先为$x_1$找配对。第一条边是$(x_1,y_1)$，标记！

在没有遇到冲突之前，我们都这样做：

这个时候冲突了，$x_3$的第一个是$y_1$，虽然他可以去跟$y_7$匹配，但是我们希望把这个$y_7$机会留给后人，先看看与$y_1$配对的那位兄弟$x_1$能否腾个位置出来。发现还是不可以，因为$(x_1,y_2)$，$y_2$被$x_2$占了，所以希望老哥$x_2$腾个位置，终于可以了，找到了$y_5$，从而如下：

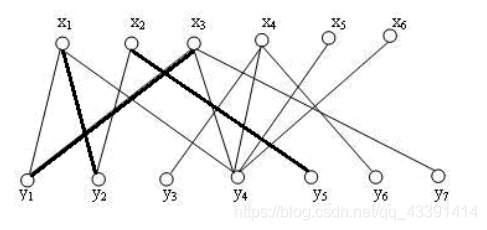
然后继续往下做，下次开始对$x_4$进行匹配，就这样下去…。

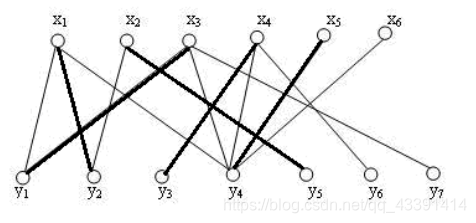
这个时候，匹配$x_6$的时候，发现$y_4$被人占了，被$x_5$占了，而$x_5$只能匹配它，腾不出位置来了，所以$x_6$只有一个单着了。
其实，到这里，我们发现，即使$x_5$把$y_4$让给$x_6$，最大匹配数还是和之前一样，保持不变，这初步验证了匈牙利算法的正确性，但是仍然不严格。

下面给出匈牙利算法的证明。

参考资料：
https://blog.csdn.net/smartxxyx/article/details/9275177
https://blog.csdn.net/Dark_Scope/article/details/8880547?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control
https://blog.csdn.net/u013384984/article/details/90718287