显式欧拉法求解常微分方程

我们求解的微分方程对象是如下这样的，左边是导数，右边是$f(x,y)$。例如：

那么显式欧拉法的迭代步骤如下：（注意，显式欧拉法不是求解$y(x)$的，而是求解一系列的点$(x_i,y_i)$，这些和真实函数中的点非常接近。）

其思想如下：

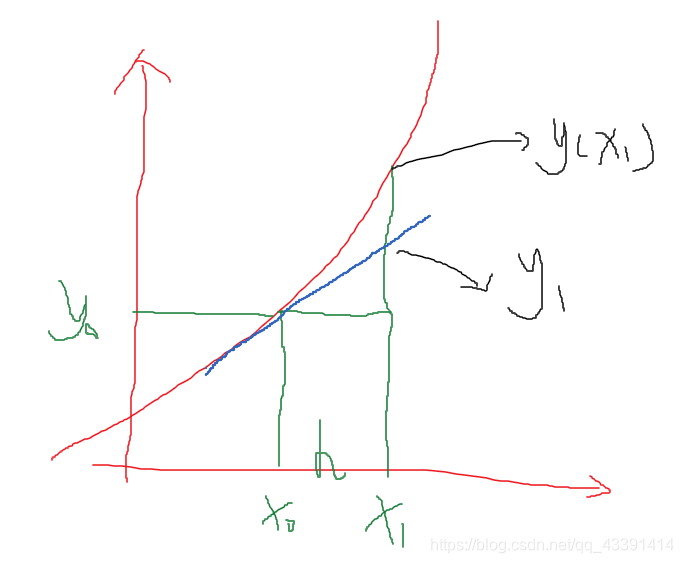
我们要解形如$y^{\prime }=f(x,y)$这样的微分方程。

上如揭示了其奥秘。

一般你自己做微分方程的题的时候，我们都有初值，例如$y(1)=1$，那么在我们这里就令$x_0=1,y_0=1$。然后你随便确定一个$h$，得到$x_1=x_0+h$，计算一下这个点的函数值$y$，即计算$y(x_1)$，记为$y_1$。

但是没这么容易计算，所以我们来一个近似。

即$y_1=y0+hf(x_0,y_0)$，从而我们得到了$(x_1,y_1)$。

当然啦，有人问这个迭代式子是怎么来的，首先你要明白，给定真实曲线上的一点$(x_0,y_0)$，其切线斜率为$f(x_0,y_0)$，为什么?因为微分方程告诉你了，$y^{\prime }=f(x,y)$，左边不就是导数吗？所以等于右边。

你再看看图，就知道了，那个$y_1$是近似的，并不是真正的$y(x_1)$，然后你再看看那个更新式子，就应该明白我是如何近似计算$y(x_1)$了，以直代曲嘛。

一般，我们可以通过减小$h$来减小误差，那么两者就更加接近了。

---

我们回到开头这个问题，用这个方法来求解一下，看一下效果怎么样。

这个方程我们可以求得真实函数为：

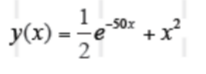
我们比较一下，用上述显式欧拉法得到的一系列点和真实函数的差别，为了效果好一点，我们取$h=0.01$,从$x_0=0$，一直计算到$x=1$，也就是计算100个点，看能不能模拟出[0,1]区间上的真实函数。

h=0.01
x0=0
y0=0.5
x_last=1
y=[]
x=[]
x.append(x0)
y.append(y0)
nowx=x0
while(x0<x_last):
    y0=y0+h*(-50*y0+50*x0*x0+2*x0)
    y.append(y0)
    x0=x0+h
    x.append(x0)

##绘制图像
testx=np.linspace(0,1,101)
testy=0.5*np.power(np.e,-50*testx)+testx*testx
figure=plt.figure(figsize=(20,8),dpi=80)
plt.plot(testx,testy,label="true")
plt.plot(x,y,label="h=0.01")
plt.legend()

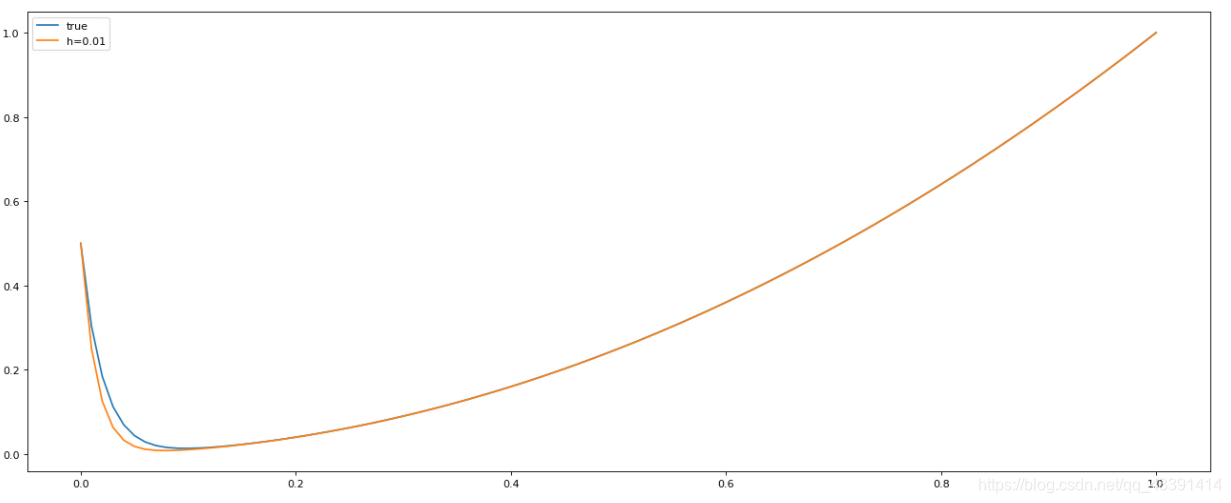
发现，当h比较小的，效果还是不错的。