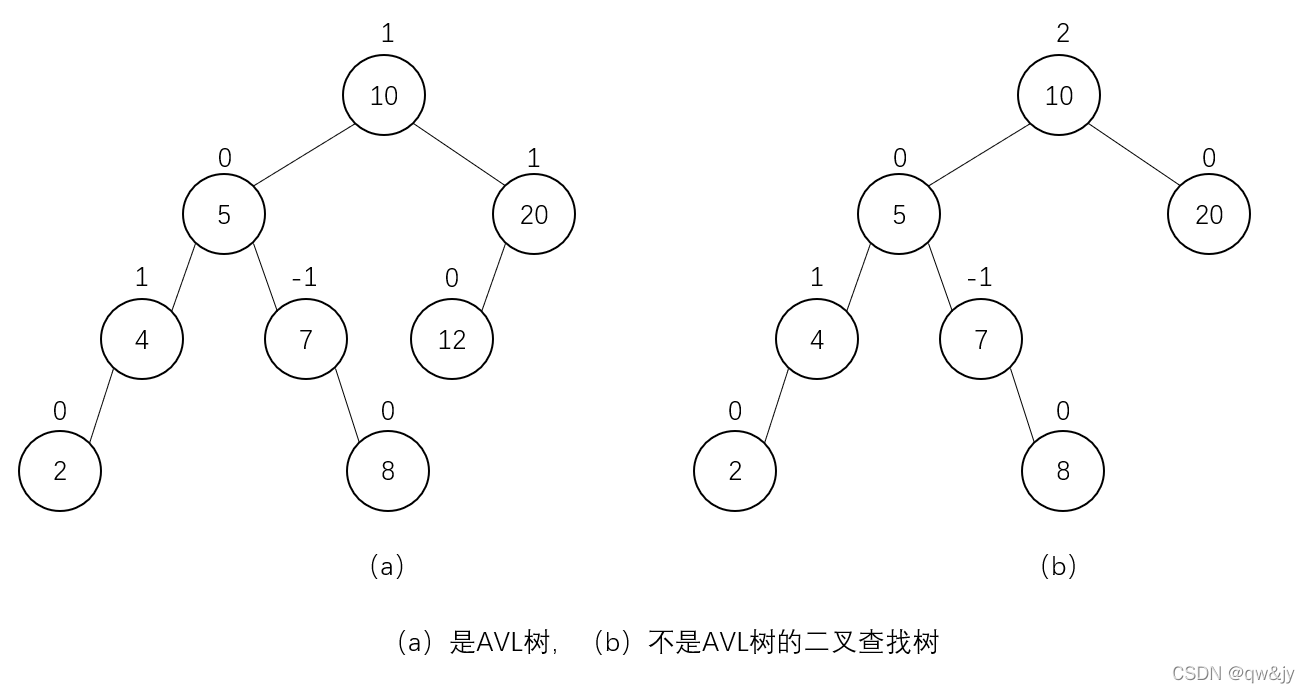
平衡二叉树*

最新推荐文章于 2024-05-20 20:08:58 发布

qwjy

最新推荐文章于 2024-05-20 20:08:58 发布

阅读量499

点赞数

文章标签：算法数据结构平衡二叉树二叉平衡树 2-3树

本文链接：https://blog.csdn.net/qq_43448856/article/details/122294613

版权

数据结构与算法专栏收录该内容

32 篇文章 10 订阅

订阅专栏

文章目录

平衡二叉树
AVL 树的旋转
代码实现
2-3 树
2-3-4树

平衡二叉树

平衡二叉树（Balanced Binary Tree）又被称为 AVL 树。
定义：一棵 AVL 树是一棵二叉查找树，其中每个节点的平衡因子（定义为该节点左子树和右子树的高度差），这个平衡因子要么为 0，要么为 +1 或者 -1 （一棵空树的高度定义为 -1，当然平衡因子也可以被定义为左右子树的叶子数的差而不是高度差）。
平衡二叉树图示

AVL 树的旋转

如果插入一个新节点使得一棵 AVL 树失去了平衡，我们可以用旋转对这棵树做一个变换。AVL 树的旋转，是以某节点为根的子树的一个本地变换，该节点的平衡要么变成了 +2，要么变成了 -2。若果有若干个这样的节点，我们先找出最靠近新插入的叶子的不平衡节点，然后旋转以该节点为根的子树。只存在 4 种类型的旋转，实际上，其中两种又是另外两种的镜像。

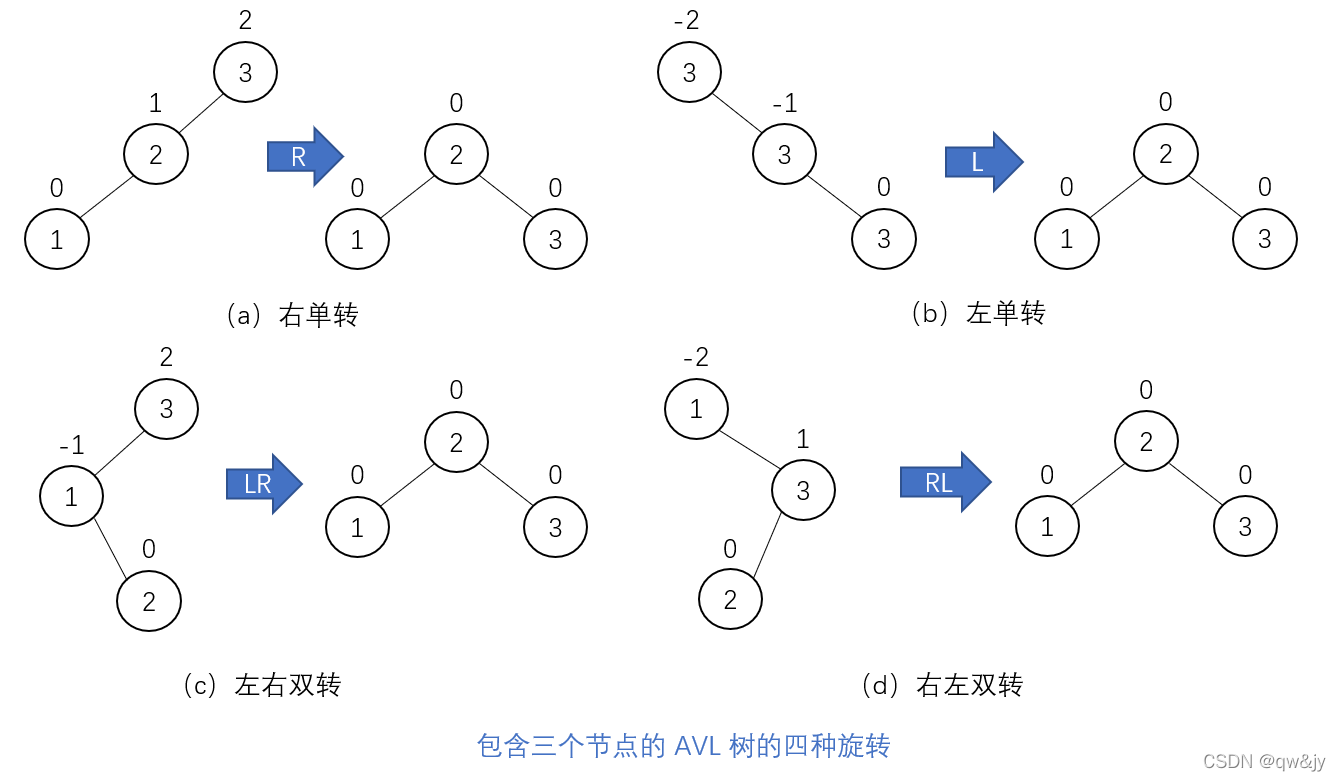
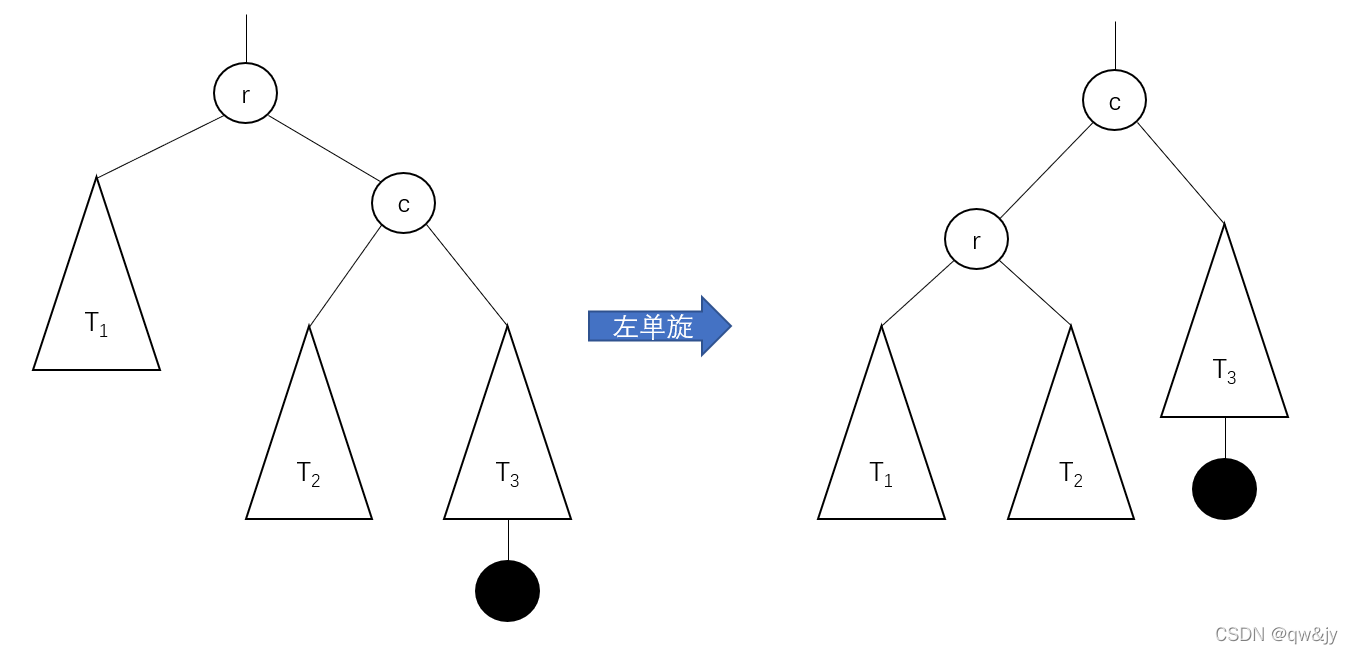
第一种旋转类型被称为向右单向旋转或者右单转。下图是右单转的最具一般性的形式。
右单转的一般形式
和右单转相对应的是向左单转旋转或者左单转，它是右单转的镜像。

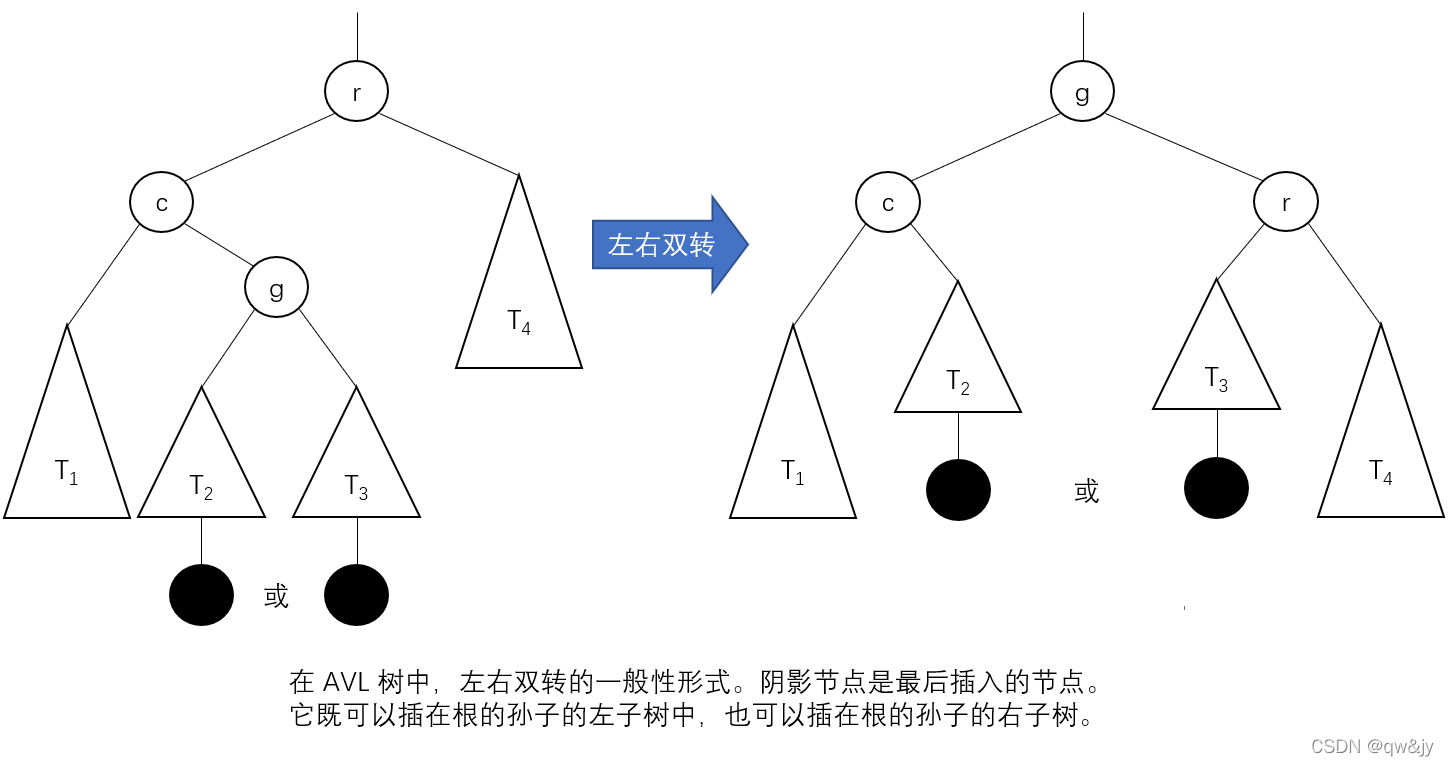
第二种旋转类型被称为双向左右旋转或者左右双转。实际上，它是两个旋转的组合：我们对根 r 的左子树进行左旋，再对这棵以 r 为根的新树进行右旋。旋转是在一个新的键插入树的左子女的右子树后发生的。在插入以前，这棵树的根的平衡因子是 +1。
左右双转的一般形式
双向右左旋转，又称右左双转，是左右双转的镜像。

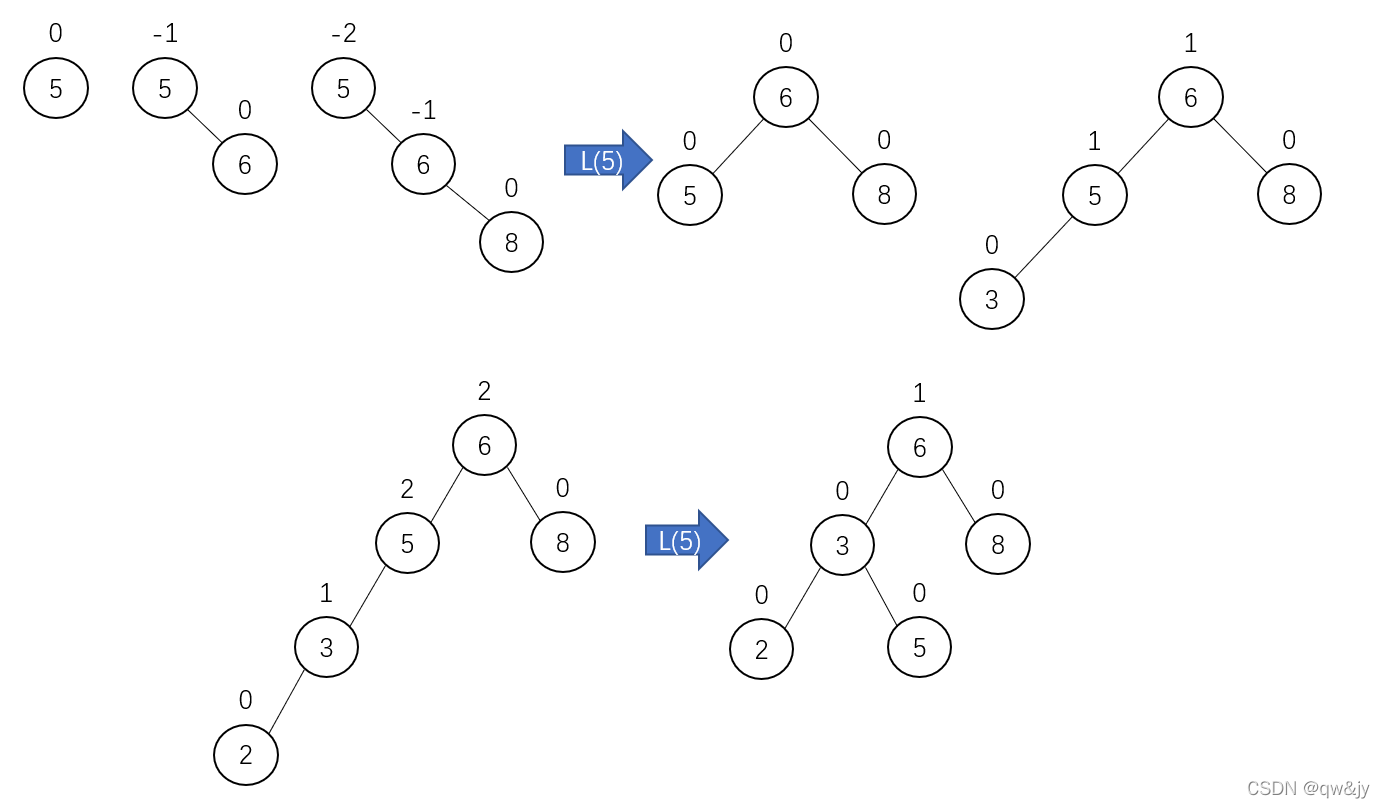
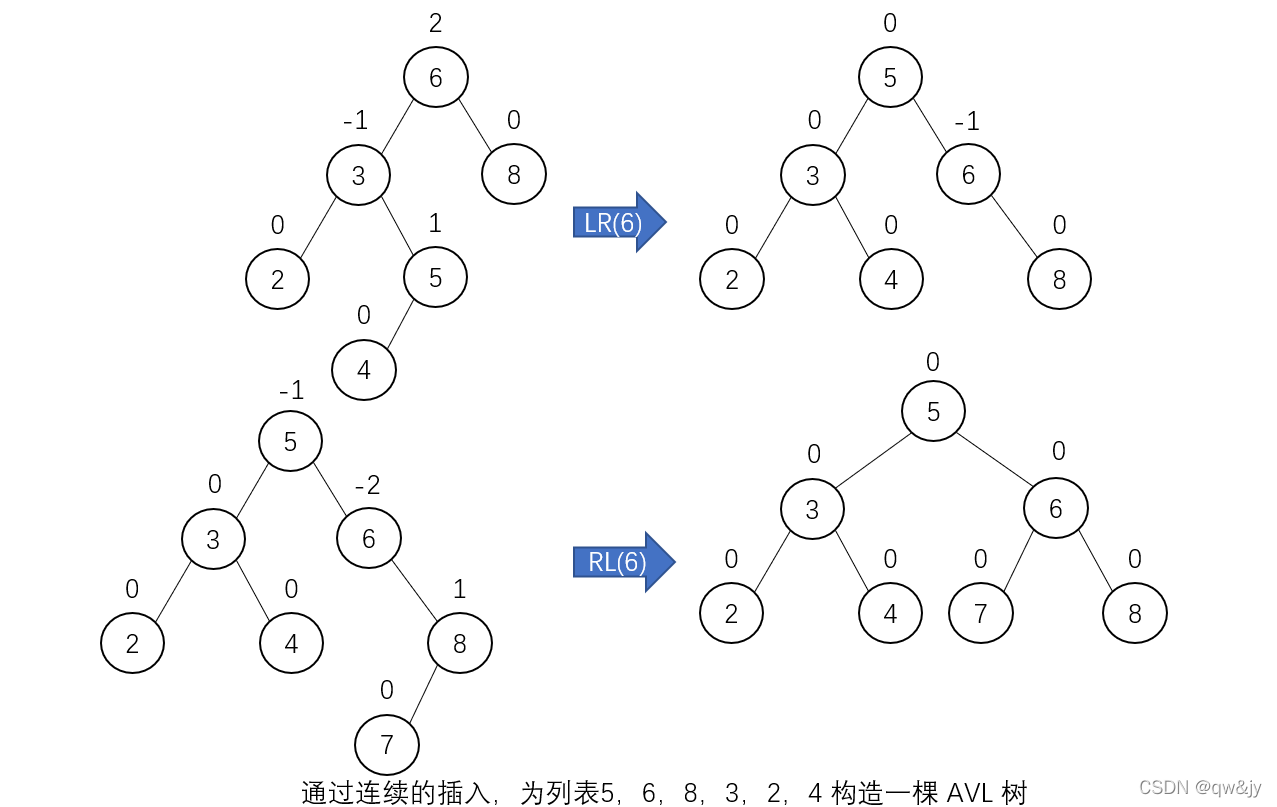
通过连续的插入，为列表5，6，8，3，2，4，7 构造一棵 AVL 树。旋转缩写字符旁括号中的数字指出了被重新组织的树的根。下面是构建 AVL 树的过程：
构建1
构建2

代码实现

定义平衡二叉树节点结构：

typedef struct Node
{
    int key;//节点数据
    struct Node *left;//左孩子
    struct Node *right;//右孩子
    int bf;//平衡因子
}BTNode, *BiTree;

右单转（R）

右单转的一般形式

BiTree R_Revolve(BiTree p){//对以p为根的二叉排序树做右单旋
	BiTree l;
	l = p->left;
	p->left = l->right;
	l->right = p;
	
	return l;
}

左单转（L）

左单旋

BiTree L_Revolve(BiTree p){//对以p为根的二叉排序树做左单旋 
	BiTree l;
	l = p->right;
	p->right = l->left;
	l->left = p;
	
	return l; 
}

左右双转（LR）

左右双转
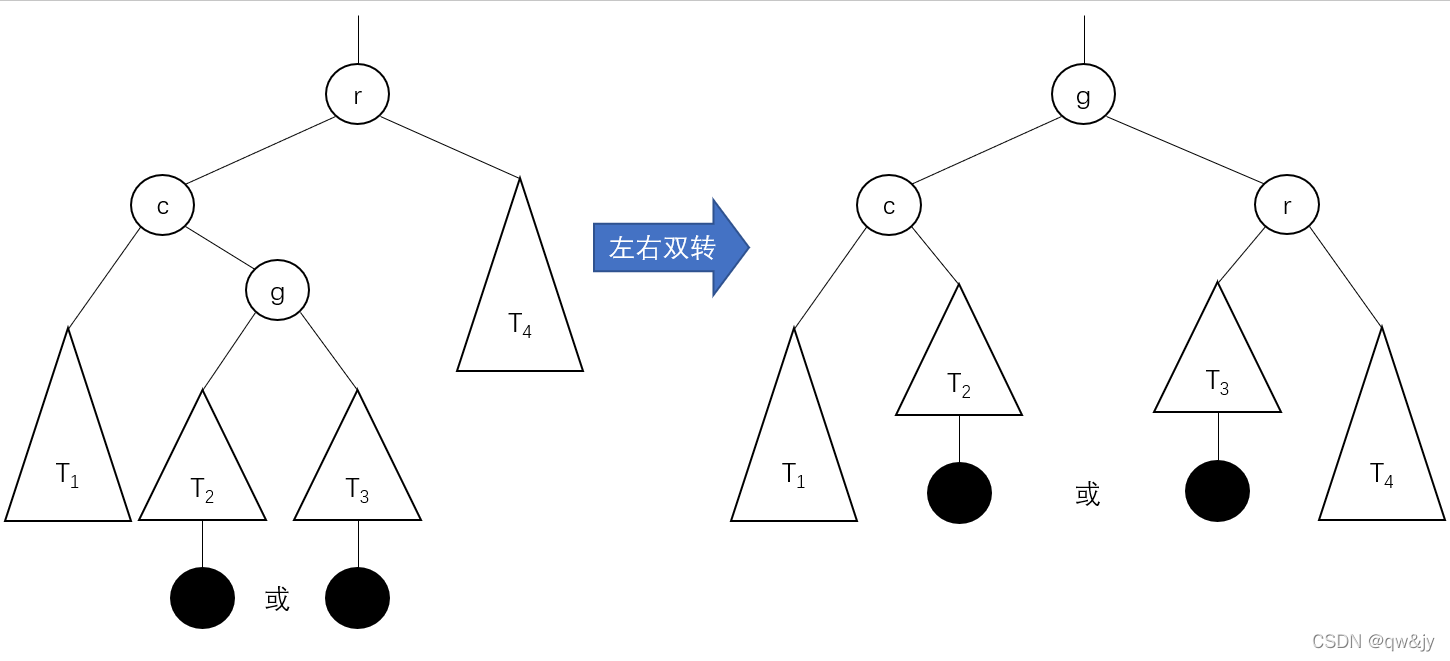
实际上就是先左旋，后右旋。

BiTree LR_Revolve(BiTree p){//对以p为根的二叉排序树做左右双转 
	BiTree l;
	l = p->left;
	p->left = L_Revolve(l);
	return R_Revolve(p);
}

右左双转（RL）

右左双转
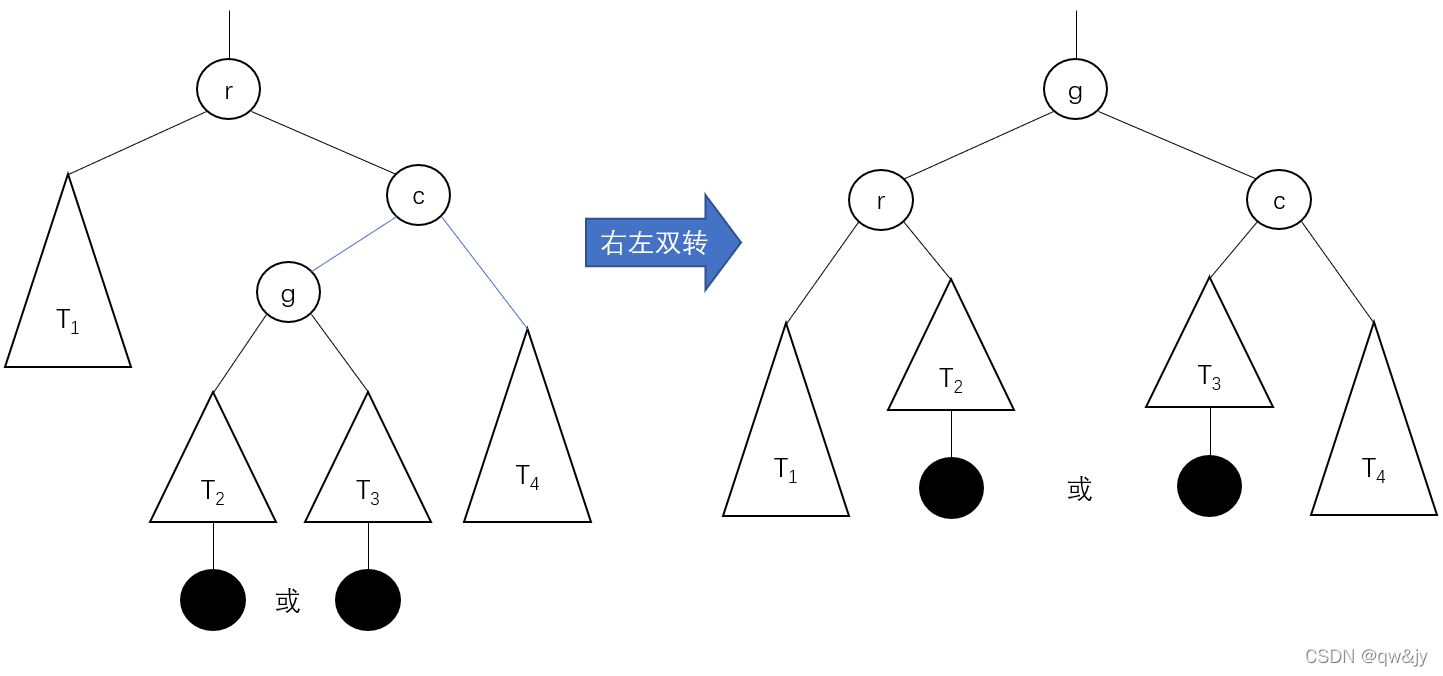
实际上就是先右旋，后左旋。

BiTree RL_Revolve(BiTree p){//对以p为根的二叉排序树做右左双转 
	BiTree l;
	l = p->right;
	p->right = R_Revolve(l);
	return L_Revolve(p); 
}

插入

typedef struct Node
{
    int key;//节点数据
    struct Node *left;//左孩子
    struct Node *right;//右孩子
    int bf;//平衡因子
}BTNode, *BiTree;

int height(BiTree p){//求树的高度 
	if(p == NULL)
		return 0;
	int l = height(p->left);
	int r = height(p->right);
	return l > r ? l+1:r+1;
}

int getBF(BiTree p){//求p结点的平衡因子 
	if(p == NULL)
		return 0;
	return height(p->left) - height(p->right);
}

BiTree newNode(int key){//创建一个新的结点，数据为key 
	BiTree p = (BiTree)malloc(sizeof(BTNode));
	p->key = key;
	p->left = NULL;
	p->right = NULL;
	p->bf = 0;
	return p;
}

BiTree R_Revolve(BiTree p){//对以p为根的二叉排序树做右单旋
	BiTree l;
	l = p->left;
	p->left = l->right;
	l->right = p;
	
	return l;
} 

BiTree L_Revolve(BiTree p){//对以p为根的二叉排序树做左单旋 
	BiTree l;
	l = p->right;
	p->right = l->left;
	l->left = p;
	
	return l; 
}

BiTree LR_Revolve(BiTree p){//对以p为根的二叉排序树做左右双转 
	BiTree l;
	l = p->left;
	p->left = L_Revolve(l);
	return R_Revolve(p);
}

BiTree RL_Revolve(BiTree p){//对以p为根的二叉排序树做右左双转 
	BiTree l;
	l = p->right;
	p->right = R_Revolve(l);
	return L_Revolve(p); 
}

BiTree insertNode(BiTree L, int key){//插入一个节点 
	if(L == NULL)
		return newNode(key);
	
	if(key < L->key)
		L->left = insert(L->left, key);
	else if(key > L->key)
		L->right = insert(L->right, key);
	else
		return L;
	
	L->bf = getBF(L);
	
	if(L->bf > 1 && key < L->left->key)//R型
		return R_Revolve(L);
	
	if(L->bf < -1 && key > L->right->key)//L型
		return L_Revolve(L);
	
	if(L->bf > 1 && key > L->left->key)//LR型
		return LR_Revolve(L);
	
	if(L->bf < -1 && key < L->right->key)//RL型
		return RL_Revolve(L);
	
	return L; 
}

删除

BiTree minKeyNode(BiTree p){//在树中找最小的结点 
	BiTree q = p;
	while(q->left != NULL)
		q = q->left;
	
	return q;
}

BiTree deleteNode(BiTree L, int key){//删除节点 
	if(L == NULL)//树为空 
		return L;
	
	if(key < L->key)//数据小于当前结点，去左子树中继续找 
		L->left = deleteNode(L->left, key);
	else if(key > L->key)//数据大于当前结点，去右子树继续找 
		L->right = deleteNode(L->right, key);
	else{//找到删除的结点 
		if(L->left == NULL || L->right == NULL){//左右子树不同时为空 
			BiTree p = L->left ? L->left : L->right;
			
			if(p == NULL){//左右子树皆为空 
				p == L;
				L = NULL;
			}
			else//一棵子树为空 
				L = p;
		}
		else{//左右子树都存在 
			BiTree p = minKeyNode(L->right);//在右子树中找到最小值顶替该点 
			L->key = p->key;
			L->right = deleteNode(L->right, p->key);//然后在右子树中删除该点 
		}
	}
	
	if(L == NULL)
		return L;
	
	L->bf = getBF(L);
	
	if(L->bf > 1 && getBF(L->left) >= 0)//R型
		return R_Revolve(L);
	
	if(L->bf < -1 && getBF(L->right) <= 0)//L型
		return L_Revolve(L);
	
	if(L->bf > 1 && getBF(L->left) < 0)//LR型
		return LR_Revolve(L);
	
	if(L->bf < -1 && getBF(L->right) > 0)//RL型
		return RL_Revolve(L);
	
	return L; 
}

2-3 树

概述

一棵 2-3 查找树或为一棵空树，或由以下结点组成：

2-结点，含有一个键（及其对应的值）和两条链接，左链接指向的 2-3 树中的键都小于该结点，右链接指向的 2-3 树中的键都大于该结点。
3-结点，含有两个键（及其对应的值）和三条链接，左链接指向的 2-3 树中的键都小于该结点，中链接指向的 2-3 树中的键都位于该结点的两个键之间，右链接指向的 2-3 树中的键都大于该结点。

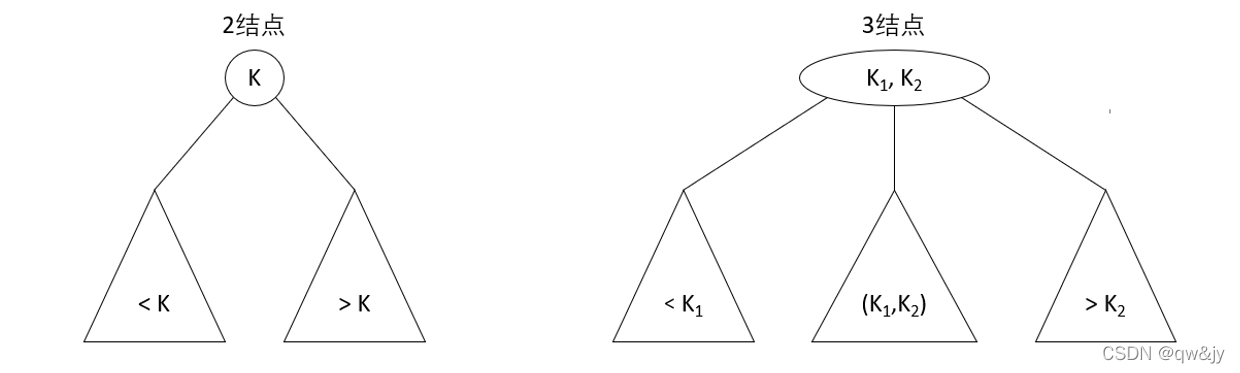
2-3 树的最后一个要求是，树中的所有叶子必须位于同一层，也就是说，一棵 2-3 树总是高度平衡的：对于每个叶子来说，从树的根到叶子的路径长度都是相同的。

查找

在 2-3 树中查找一个给定的键 K 是非常简单的，类似于二叉排序树的查找。
从根开始。如果根是一个 2 结点，我们就把它当作一个二叉排序树来操作：如果 K 等于根的键值，算法停止；如果 K 小于或大于根的键值，我们分别在左子树或右子树中继续查找。如果根是一个 3 结点，在不超过两次比较之后，可以知道，是停止查找(K 等于根的某个键值)，还是继续在根的 3 棵子树的哪一棵中继续查找。

插入

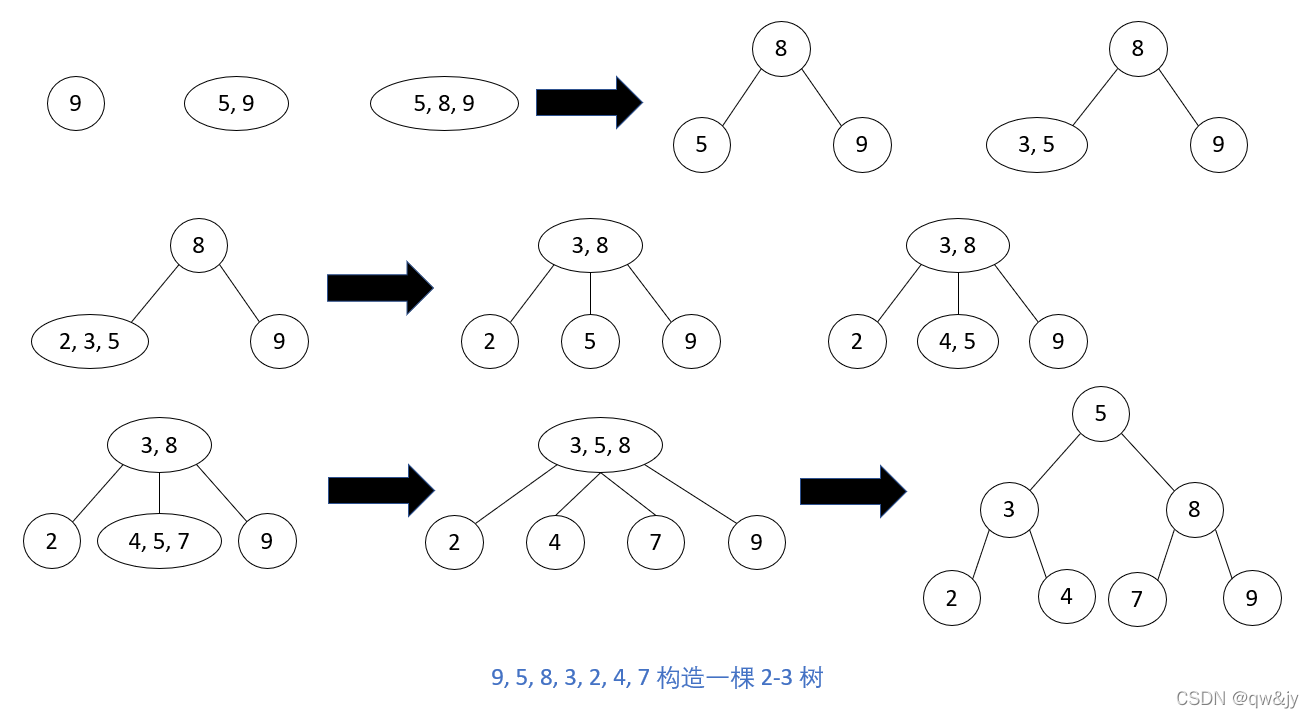
首先，除非空树，否则我们总是把一个新的键 K 插入一个叶子里。
通过查找 K 我们来确定一个合适的插入位置。如果找到的叶子是一个 2 结点，根据 K 是小于还是大于结点中原来的键，我们把 K 作为第一个键或者第二个键插入。如果找到的叶子是一个 3 结点，我们把叶子分裂成 2 个结点： 3 个键(2 个原来的键和 1 个新键)中最小的放到第一个叶子中，最大的键放到第二个叶子中，同时中间的键提升到原来叶子的父母中(如果这个叶子恰好是树的根，我们就创建一个新的根来接纳这个中间键)。注意，中间键提升到父母中可能会导致父母的溢出(如果它是一个 3 结点)，并且因此会导致沿着该叶子的祖先链条发生多个结点的分裂。
构造示例

删除

删除分为 3 种情况：

删除非叶子结点
删除不为2-节点的叶子结点
删除为2-节点的叶子结点

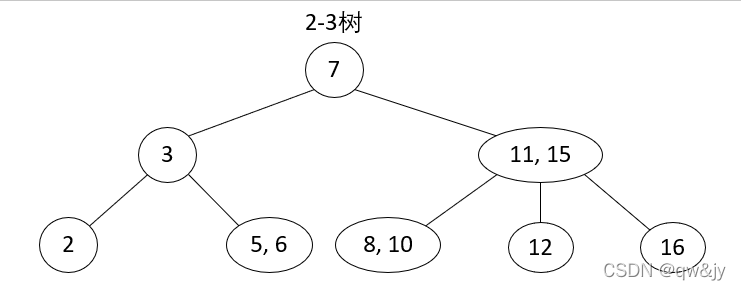
2-3树示例

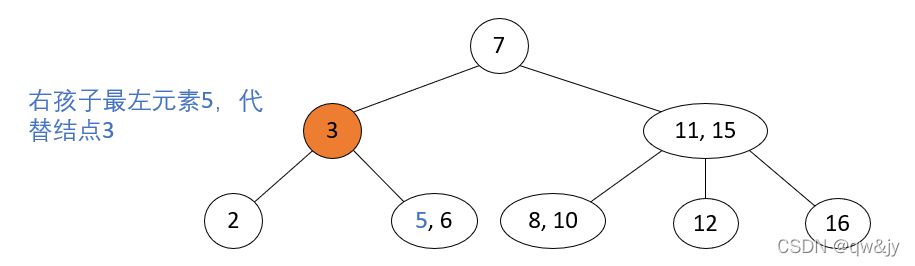
删除非叶子结点
存在步骤： 使用右孩子的最左 key 来覆盖当前待删除结点 key，再删除用来覆盖的 key 值。
删除非叶子结点1
删除非叶子结点2

删除非叶子结点3

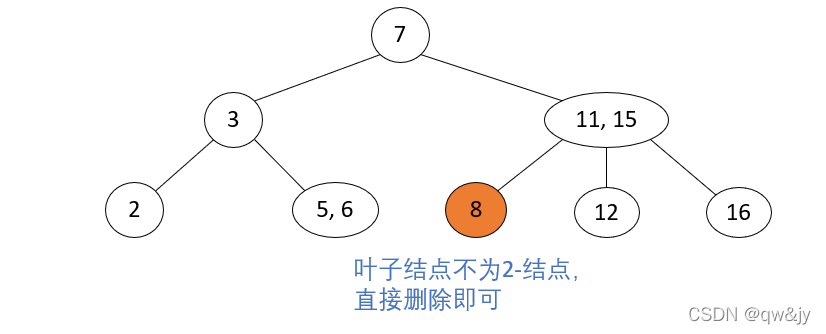
删除不为2-结点的叶子结点
操作步骤： 删除不为2-结点的叶子结点，直接删除结点即可。
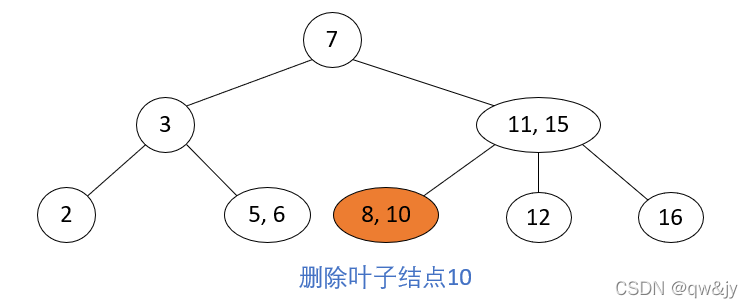
删除不为2-结点的叶子结点1
删除不为2-结点的叶子结点2

删除为2-结点的叶子结点
分为四种情况：

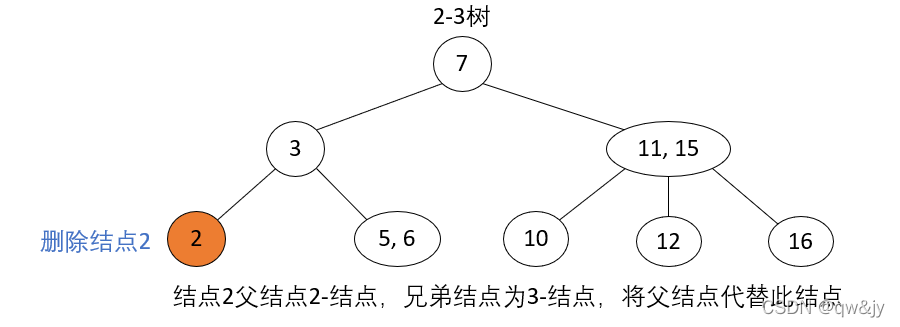
删除结点为2-结点，父结点为2-结点，兄弟结点为3-结点
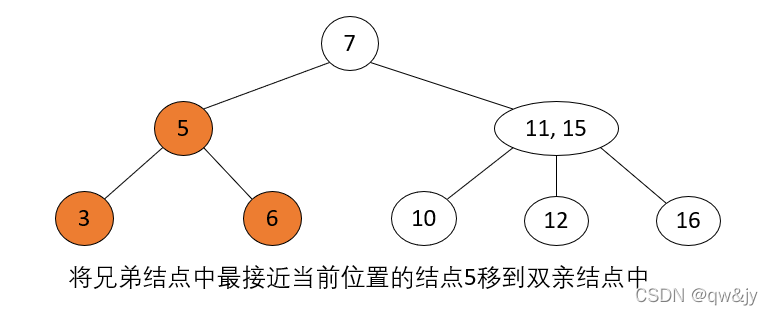
操作步骤： 当前待删除结点的父结点是2-结点、兄弟结点是3-结点，将父结点移动到当前待删除结点位置，再将兄弟结点中最接近当前位置的 key 移动到父结点中。
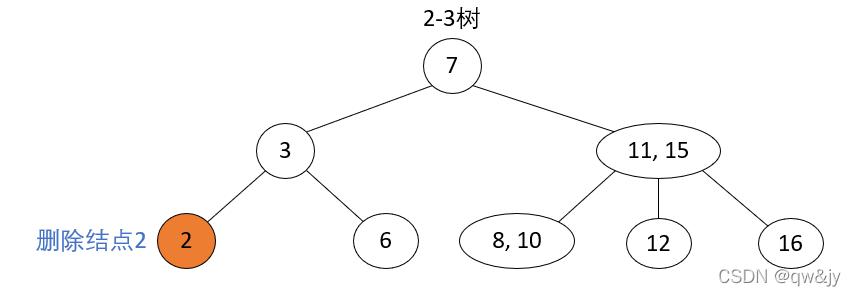
删除结点为2-结点，父结点为2-结点，兄弟结点为2-结点
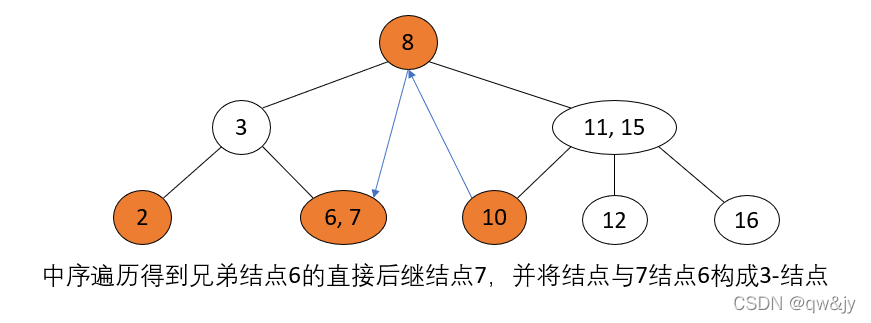
操作步骤： 当前待删除结点的父结点是2-结点、兄弟结点是2-结点，先通过移动兄弟结点的中序遍历直接后驱到兄弟结点，以使兄弟结点变为3-结点；再进行 1 的操作。
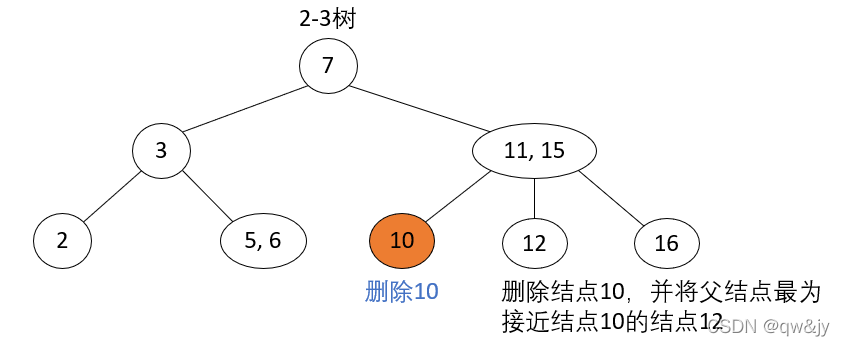
删除结点为2-结点，父结点为3-结点
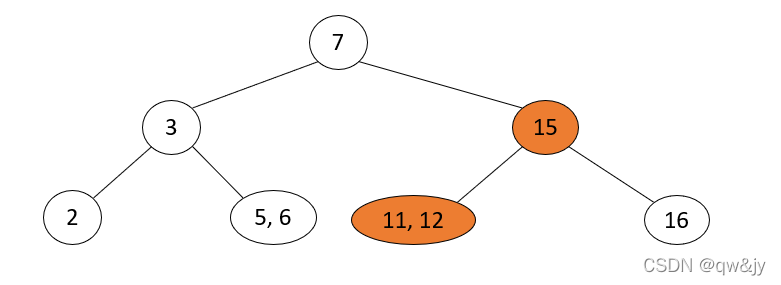
操作步骤： 当前待删除结点的父结点是3-结点，拆分父结点使其成为2-结点，再将父结点中最接近的一个拆分 key 与中孩子合并，将合并后的结点作为当前结点。
2-3树为满二叉树，删除叶子结点
操作步骤： 若2-3树是一棵满二叉树，将2-3树层树减少，并将当前删除结点的兄弟结点合并到父结点中，同时将父结点的所有兄弟结点合并到父结点的父结点中，如果生成4-结点，再分解4-结点。

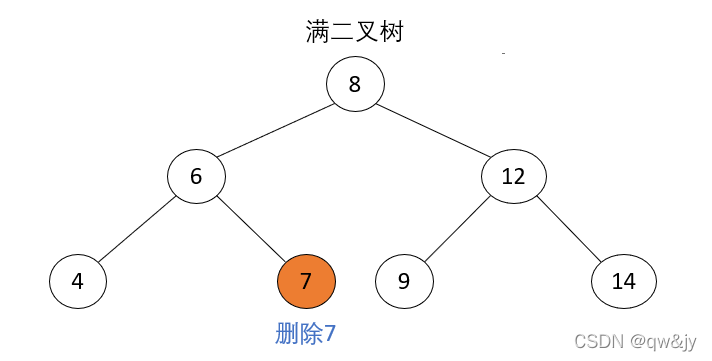
2-3树为满二叉树，将2-3树的层数减少，将兄弟结点 4 上移至父结点 7，同时将父结点 7 的所有兄弟结点 12 上移至父结点的父结点 8。

分析

一棵包含 n 个键、高度为 h 的 2-3 树。
$\log _{3}\left( n+1\right) -1\leq h\leq \log _{2}\left( n+1\right) -1$
所以无论在最坏情况还是在一般情况下，2-3 树的查找、插入和删除的时间效率都属于 O(logn)。

2-3-4树

概述

一棵 2-3-4 查找树或为一棵空树，或由以下结点组成：

2-结点，含有一个键（及其对应的值）和两条链接，左链接指向的 2-3-4 树中的键都小于该结点，右链接指向的 2-3-4 树中的键都大于该结点。
3-结点，含有两个键（及其对应的值）和三条链接，左链接指向的 2-3-4 树中的键都小于该结点，中链接指向的 2-3-4 树中的键都位于该结点的两个键之间，右链接指向的 2-3-4 树中的键都大于该结点。
4-结点，含有三个键（及其对应的值）和四条链接，第一条链接指向的 2-3-4 树中的键都小于该结点，第二条链接指向的 2-3-4 树中的键都位于该结点的前两个键之间，第三条链接指向的 2-3-4 树中的键都位于该结点的后两个键之间，第四条链接指向的 2-3-4 树中的键都大于该结点。

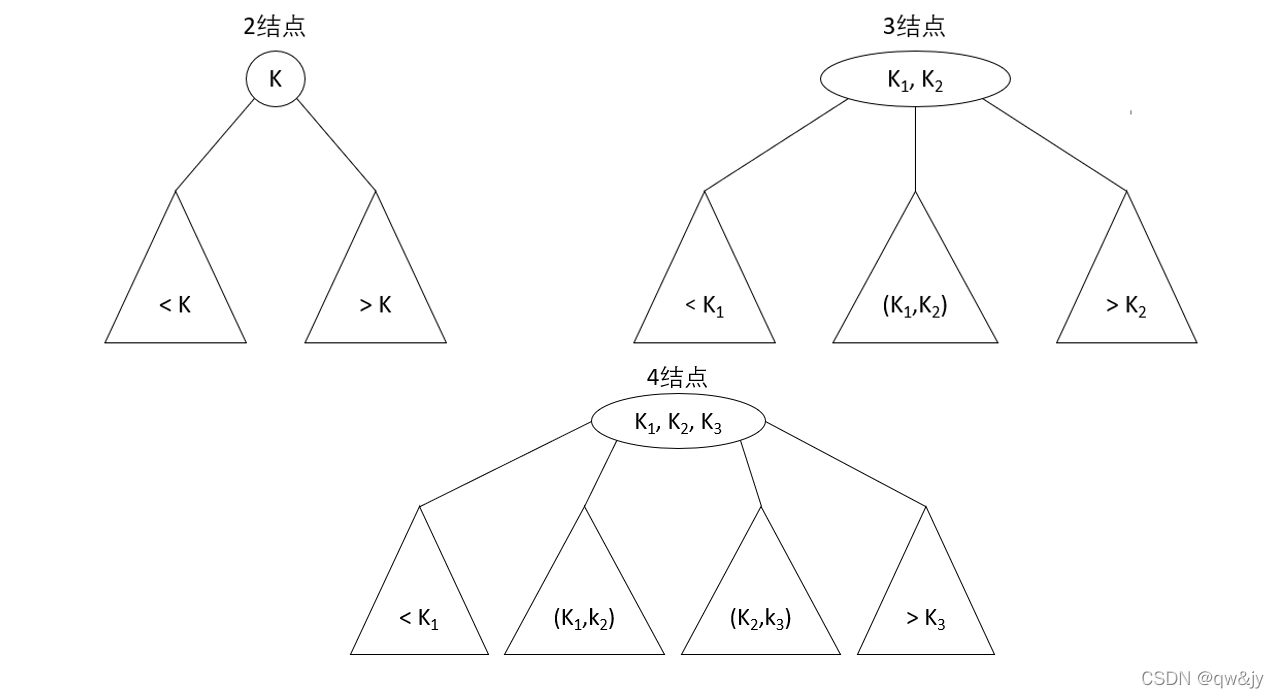
2-3-4 树的最后一个要求是，树中的所有叶子必须位于同一层，也就是说，一棵 2-3-4 树总是高度平衡的：对于每个叶子来说，从树的根到叶子的路径长度都是相同的。

查找

在 2-3-4 树中查找一个给定的键 K 是非常简单的，类似于二叉排序树的查找。
从根开始。如果根是一个 2 结点，我们就把它当作一个二叉排序树来操作：如果 K 等于根的键值，算法停止；如果 K 小于或大于根的键值，我们分别在左子树或右子树中继续查找。如果根是一个 3 结点，在不超过两次比较之后，可以知道，是停止查找(K 等于根的某个键值)，还是继续在根的 3 棵子树的哪一棵中继续查找。如果根是一个 4 结点，在不超过三次比较之后，可以知道，是停止查找(K 等于根的某个键值)，还是继续在根的 4 棵子树的哪一棵中继续查找。

插入

首先，除非空树，否则我们总是把一个新的键 K 插入一个叶子里。
通过查找 K 我们来确定一个合适的插入位置。如果找到的叶子是一个 2- 结点或 3- 结点，根据 K 是小于还是大于结点中原来的键，我们把 K 作为一个键。
2-3-4树插入

qwjy

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
平衡二叉树*

 文章目录平衡二叉树AVL 树的旋转   平衡二叉树平衡二叉树（Balanced Binary Tree）又被称为 AVL 树。定义：一棵 AVL 树是一棵二叉查找树，其中每个节点的平衡因子（定义为该节点左子树和右子树的高度差），这个平衡因子要么为 0，要么为 +1 或者 -1 （一棵空树的高度定义为 -1，当然平衡因子也可以被定义为左右子树的叶子数的差而不是高度差）。  AVL 树的旋转...
复制链接

扫一扫