第十二届蓝桥杯 2021年省赛真题 (Java 大学C组) 第一场

---

_Placeholder

---

#A ASC

本题总分：5 分

---

问题描述

  已知大写字母 $A$ 的 $ASCII$ 码为 $65$，请问大写字母 $L$ 的 $ASCII$ 码是多少？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

76

calcCode：

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() {
        // System.out.println(65 + 'L' - 'A');
        System.out.println((int)'L');
    }
}

?这是什么新型攻击性言论

---

#B 空间

本题总分：5 分

---

问题描述

  小蓝准备用 $256\mathrm{M}\mathrm{B}$ 的内存空间开一个数组，数组的每个元素都是 $32$ 位二进制整数，如果不考虑程序占用的空间和维护内存需要的辅助空间，请问 $256\mathrm{M}\mathrm{B}$ 的空间可以存储多少个 $32$ 位二进制整数？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

67108864

calcCode：

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() {
        System.out.print(256 >> 2 << 20);
    }
}

  结果填空双签到了属于是。

  $\mathrm{M}\mathrm{B}$ 全称 兆字节$(\mathrm{M}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{B}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s})$，

  而 $1\mathrm{B}\mathrm{y}\mathrm{t}\mathrm{e}=8\mathrm{b}\mathrm{i}\mathrm{t}\mathrm{s}$，也就是一个 $32$ 位整形占用 $4\mathrm{B}\mathrm{y}\mathrm{t}\mathrm{e}$。

  同时 $1\mathrm{M}\mathrm{B}=2^{10}\mathrm{K}\mathrm{B}=2^{20}\mathrm{B}$，

  将 $256$ 除 $4$ 再乘以 $2^{20}$ 就行了。

---

#C 卡片

本题总分：10 分

---

问题描述

  小蓝有很多数字卡片，每张卡片上都是数字 $0$ 到 $9$。
  小蓝准备用这些卡片来拼一些数，他想从 $1$ 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。
  小蓝想知道自己能从 $1$ 拼到多少。
  例如，当小蓝有 $30$ 张卡片，其中 $0$ 到 $9$ 各 $3$ 张，则小蓝可以拼出 $1$ 到 $10$，但是拼 $11$ 时卡片 $1$ 已经只有一张了，不够拼出 $11$。
  现在小蓝手里有 $0$ 到 $9$ 的卡片各 $2021$ 张，共 $20210$ 张，请问小蓝可以从 $1$ 拼到多少？
  提示：建议使用计算机编程解决问题。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

3181

---

朴素解法

---

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() { System.out.println(calc(2021)); }

    int calc(int upper) {
        int[] count = new int[10];
        for (int n = 1, k = 1; ; k = ++n)
            do
                if (++count[k % 10] > upper)
                	return n - 1;
            while ((k /= 10) > 0);
    }
}

  没什么好说的。

---

弯道超车

---

  观察 $[1,9]$ 这个区间中，$[0,9]$ 的出现情况。

  在 $[1,9]$ 中，$1$ 至 $9$ 各出现 $1$ 次。

  把观察的范围扩大到 $[1,99]$，十位的 $1$ 出现 $[10,19]$ 共 $10$ 次，十位的 $2$ 出现 $[20,29]$ 共 $10$ 次，$\cdots$ ，十位的 $9$ 出现 $[90,99]$ 共 $10$ 次，低位 $[0,9]$ 重复出现 $10$ 次，$1$ 至 $9$ 各出现 $20$ 次，$0$ 出现 $9$ 次。

  将这个观察范围继续扩大，会发现 $1$ 的使用次数总是不小于 $0$ 、 $2$ 至 $9$，也就是说统计 $0$ 、 $2$ 至 $9$ 是没有意义的。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() { System.out.println(calc(20)); }

    int calc(int upper) {
        int count = 0;
        for (int n = 1, k = 1; ; k = ++n) {
            do
                if (k % 10 == 1) count++;
            while ((k /= 10) > 0);
            if (count > upper) return n - 1;
        }
    }
}

---

#D 相乘

本题总分：10 分

---

问题描述

  小蓝发现，他将 $1$ 至 $1000000007$ 之间的不同的数与 $2021$ 相乘后再求除以$1000000007$ 的余数，会得到不同的数。
  小蓝想知道，能不能在 $1$ 至 $1000000007$ 之间找到一个数，与 $2021$ 相乘后再除以$1000000007$ 后的余数为 $999999999$。如果存在，请在答案中提交这个数；
  如果不存在，请在答案中提交 $0$。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

17812964

---

朴素解法

---

  朴素的去枚举 $[1,1000000007]$ 中的每一个数，看似不明智，但实际上，

  对于现代的 $\mathrm{C}\mathrm{P}\mathrm{U}$ 来说，就是洒洒水。

  就算你的 $\mathrm{C}\mathrm{P}\mathrm{U}$ 主频低至 $2.0\mathrm{G}\mathrm{h}\mathrm{z}$，那也是每秒钟二十亿次的计算速度。

  不要小瞧了现代计算机啊，混蛋。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 1000000007, M = 999999999;

    void run() {
        for (int i = 1; i <= N; i++)
            if (i * 2021L % N == M) System.out.println(i);
    }
}

---

余数定义

---

  余数的定义是，

  给定两个整数 $a$、$b$，其中 $b\ne 0$，那么一定存在两个唯一的整数 $q$、$r$，使得$$a=qb+r，0\le r<|b|$$

  而在这道题中，我们最后要找的，可能存在的这个数字可表示为，

  $2021\cdot a^{\prime }=1000000007\cdot q+999999999$，

  显然 $q$ 不会超过 $2021$，

  这样我们就能大大的减少枚举范围。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    long N = 1000000007, M = 999999999;

    void run() {
        for (int i = 1; i < 2021; i++)
            if ((i * N + M) % 2021 == 0)
                System.out.println((i * N + M) / 2021);
    }
}

---

扩展欧几里得算法

---

  有丶超纲。

  依题意，有同余线性方程：

  $a\times x\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}n)$，$\gcd (a,n)\mid b$

  将 $2021$ 代入 $a$，$1000000007$ 代入 $n$，$\gcd (a,n)=1$，方程有无穷解。

---

  稍微解释一下，

  $a\times x\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}n)$ 可改写为 $a\times x+n\times y=b$，

  用扩展欧几里得算法求出一组数 $x_0,y_0$，使得 $a\times x_0+n\times y_0=\gcd (a,n)$，

  则 $x=\frac{b\times x_0}{\gcd (a,n)}$ 是原方程的一个解。

  通解为 $\overline{\frac{b\times x_0}{\gcd (a,n)}\mathrm{m}\mathrm{o}\mathrm{d}n}(\mathrm{m}\mathrm{o}\mathrm{d}n)$，

  人话一点就是模 $n$ 与 $x$ 同余的同余类。

def exgcd(a, b):
    if b == 0:
        return (1, 0, a)
    (x, y, d) = exgcd(b, a % b)
    return (y, x - a // b * y, d);

(x, y, d) = exgcd(2021, 1000000007)
print((x * 999999999 // d) % (1000000007 // d))

  毕竟是结果填空题，

  就用 $\mathrm{P}\mathrm{y}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{n}$ 写了，

  虽然不喜欢这门语言，但在解决这类问题上，

  $\mathrm{P}\mathrm{y}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{n}$ 的综合效率还是要高点。

---

#E 路径

本题总分：15 分

---

问题描述

  小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
  小蓝的图由 $2021$ 个结点组成，依次编号 $1$ 至 $2021$。对于两个不同的结点 $a,b$，如果 $a$ 和 $b$ 的差的绝对值大于 $21$，则两个结点之间没有边相连；如果 $a$ 和 $b$ 的差的绝对值小于等于 $21$，则两个点之间有一条长度为 $a$ 和 $b$ 的最小公倍数的无向边相连。
  例如：结点 $1$ 和结点 $23$ 之间没有边相连；结点 $3$ 和结点 $24$ 之间有一条无向边，长度为 $24$；结点 $15$ 和结点 $25$ 之间有一条无向边，长度为 $75$。
  请计算，结点 $1$ 和结点 $2021$ 之间的最短路径长度是多少。
  提示：建议使用计算机编程解决问题。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

10266837

---

  题目已经说的够清楚了，

  建一个有 $2021$ 个顶点 $21\times 2000+\frac{21(21+1)}{2}$ 条边的无向图，跑图上的算法就完事了。

  还有的细节就是整形是否会溢出，我们取 $(1,2021]$ 中最大的质数 $2017$ 与 $2021^2$ 相乘，得到的结果还是有点夸张的，虽然经过测试，可能的线路权值合至多不会超过 $2^{31}-1$，但毕竟是面向竞赛，考虑甄别的时间成本，直接使用长整形更为划算。

---

搜索

---

深度优先搜索

---

  $2021$ 个顶点，绝大多数顶点都连有 $2\times 21$ 条边，

  别深搜了，一搜就是

  compilaition completed successfully in 500ms(4 hour ago)

  就，电脑跟选手对着坐牢。

---

记忆化搜索

---

  深度优先搜索，在搜索最优结果时，通常需要完整的枚举全部可能的问题状态。

  但在这个问题状态的集合中，所有可选方案的 “后缀” 都是相同，也就是所有可选的分支，它们都是以同一个节点结尾。

  如果我们将已经搜索到的节点到目标节点间的最短路径保存下来，在再次搜索到这个 “后缀” 的分支时直接返回。

  那么问题就可能在一个较短的时间内解决。

  这也是所谓的记忆化搜索。

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    int[] weight = new int[N + 1];

    List<Edge>[] graph = new List[N + 1];

    boolean[] visited = new boolean[N + 1];

    void run() {
        for (int i = 1; i <= N; i++)
            graph[i] = new ArrayList();
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        visited[1] = true;
        System.out.println(dfs(1));
    }

    int dfs(int v) {
        if (v == N) return 0;
        if (weight[v] != 0) return weight[v];
        int min = 0x7FFFFFFF;
        for (Edge edge : graph[v]) {
            if (visited[edge.w]) continue;
            visited[edge.w] = true;
            min = min(min, dfs(edge.w) + edge.weight);
            visited[edge.w] = false;
        }
        return weight[v] = min;
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }
}

---

枝剪广搜

---

  其实朴素的去搜索，不论深搜还是广搜，在竞赛里都是很冒进的行为，

  影响这两个算法执行效率的因素太多。

  当然要是没有其他的思路，也只能死马当活马医了。

  幸运的是，只需简单的枝剪，就能在很短的时间计算出结果

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Queue;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;
    
    void run() {
        List<Edge>[] graph = new List[N + 1];
        long[] visited = new long[N + 1];
        for (int i = 1; i <= N; i++)
            graph[i] = new ArrayList();
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        Queue<Vertex> queue = new PriorityQueue();
        Arrays.fill(visited, Long.MAX_VALUE);
        queue.offer(new Vertex(1, 0));
        Vertex V = null;
        while (queue.size() > 0) {
            V = queue.poll();
            if (V.v == N) break;
            if (V.weight >= visited[V.v]) continue;
            visited[V.v] = V.weight;
            for (Edge edge : graph[V.v])
                queue.offer(new Vertex(edge.w, edge.weight + V.weight));
        }
        System.out.println(V.weight);
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }

    class Vertex implements Comparable<Vertex> {

        int v;
        long weight;

        Vertex(int v, long weight) {
            this.weight = weight;
            this.v = v;
        }

        @Override
        public int compareTo(Vertex V) { return Long.compare(this.weight, V.weight); }
    }
}

---

双向搜索

---

  很容易就能发现，越是编号大的节点，连接着它的边的权重可能越大。

  也就是在最短路径的这条分支中，越是靠近目标节点，就越可能进入无效的分支。

  通常，在这个数据规模下，不带策略的去广搜是致命的。

  一种常见的优化方法是从源点和终点双向开始搜索，当两条分支相遇时，即视为找到了最短路径。

  由于这种问题可选择的解法有很多，这里便不做展开。

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Queue;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        List<Edge>[] graph = new List[N + 1];
        long[] visited0 = new long[N + 1];
        long[] visited1 = new long[N + 1];
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList();
            visited0[i] = visited1[i] = Long.MAX_VALUE;
        }
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        Queue<Vertex> queue = new PriorityQueue();
        queue.offer(new Vertex(N, 0, false));
        queue.offer(new Vertex(1, 0));
        Vertex V = null;
        while (true) {
            V = queue.poll();
            if (V.fromHead) {
                if (visited1[V.v] != Long.MAX_VALUE) break;
                if (V.weight >= visited0[V.v]) continue;
                visited0[V.v] = V.weight;
            } else {
                if (visited0[V.v] != Long.MAX_VALUE) break;
                if (V.weight >= visited1[V.v]) continue;
                visited1[V.v] = V.weight;
            }
            for (Edge edge : graph[V.v])
                queue.add(new Vertex(edge.w, edge.weight + V.weight, V.fromHead));
        }
        System.out.println(V.weight + (V.fromHead ? visited1[V.v] : visited0[V.v]));
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }

    class Vertex implements Comparable<Vertex> {

        int v;
        long weight;
        boolean fromHead;

        Vertex(int v, long weight) { this(v, weight, true); }

        Vertex(int v, long weight, boolean fromHead) {
            this.fromHead = fromHead;
            this.weight = weight;
            this.v = v;
        }

        @Override
        public int compareTo(Vertex V) { return Long.compare(this.weight, V.weight); }
    }
}

---

单源最短路径

---

Dijkstra

---

  题目给出的图显然是个边加权，权重非负的无向图，跑遍 $Dijkstra$ 就完事了。

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Queue;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        boolean[] marked = new boolean[N + 1];
        List<Edge>[] graph = new List[N + 1];
        long[] distTo = new long[N + 1];
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList();
            distTo[i] = Long.MAX_VALUE;
        }
        for (int v = 1; v <  N; v++)
            for (int w = v + 1; w <= min(v + 21, N);  w++) {
                graph[v].add(new Edge(w, lcm(v, w)));
                graph[w].add(new Edge(v, lcm(v, w)));
            }
        Queue<Vertex> queue = new PriorityQueue();
        queue.offer(new Vertex(1, distTo[1] = 0));
        while (queue.size() > 0) {
            Vertex V = queue.poll();
            if (marked[V.v])
                    continue;
            marked[V.v] = true;
            for (Edge edge : graph[V.v])
                if (distTo[edge.w] > distTo[V.v] + edge.weight)
                    queue.offer(new Vertex(edge.w, distTo[edge.w] = distTo[V.v] + edge.weight));
        }
        System.out.println(distTo[N]);
    }

    int min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

    class Edge {

        int w, weight;

        Edge(int w, int weight) {
            this.weight = weight;
            this.w = w;
        }
    }

    class Vertex implements Comparable<Vertex> {

        int v;
        long dist;

        Vertex(int v, long dist) {
            this.dist = dist;
            this.v = v;
        }

        @Override
        public int compareTo(Vertex V) { return Long.compare(this.dist, V.dist); }
    }
}

---

Floyd

---

  如果是一道最短路径的结果题。

  竞赛时限内能运行完 $O(n^3)$ 的程序。

  那其实无脑套 $Floyd$ 就行。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        long[][] floyd = new long[N + 1][N + 1];
        for (int v = 1; v < N; v++)
            for (int w = v + 1; w <= min(N, v + 21); w++)
                floyd[v][w] = floyd[w][v] = lcm(v, w);
        for (int k = 1; k <= N; k++)
            for (int v = 1; v <= N; v++)
                if (floyd[v][k] == 0) continue;
                else for (int w = 1; w <= N; w++)
                    if (floyd[k][w] == 0) continue;
                    else if (floyd[v][w] == 0 || floyd[v][k] + floyd[k][w] < floyd[v][w])
                        floyd[v][w] = floyd[v][k] + floyd[k][w];
        System.out.println(floyd[1][N]);
    }

    long min(int a, int b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
}

  半分钟就出来了，还行。

---

A*

---

  隐隐觉得能找到一些有启发性的性质。

  推了一下午狗屁没推出来，就当在这开个坑把。

在这里插入代码片

---

动态规划

---

  受不同的图性质影响，通常最短路径问题难以在线性时间内用动态规划解决。

  但这里给定无向图，

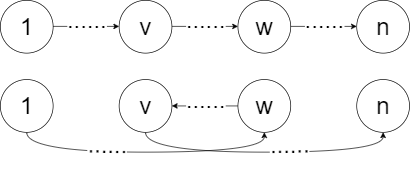
  我们将最短路径上的节点按升序排列，对于任意 $v$、$w$，$1<v<w<n$ 只存在以下两种情况：

  但只有序号的绝对差小于等于 $21$ 时，两个节点之间才存在边，即二图情况的前提条件是 $1<v<w\le 22$，将其推广至 $1\le x<v<w<y\le n$ 的情况，

  显然，从源点到任意点 $V$ 的最短路径只会从 $[V-21,V+21]$ 中产生，我们先顺序的求出每个 $W=V+21$ 较优路径，再用每个 $W$ 对 $[W-21,W)$ 间的节点进行松弛，松弛完毕时 $(1,V]$ 间的路径已是最优。

  综上有状态转移方程：

   d p ( i ) = min ⁡ { d p ( j ) + l c m ( i , j ) } dp(i) = \min\{dp(j) + lcm(i, j)\} dp(i)=min{dp(j)+lcm(i,j)}，$i>j\ge i-21$

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2021;

    void run() {
        long[] dp = new long[N + 1];
        for (int w = 2; w <= N; w++) {
            dp[w] = Long.MAX_VALUE;
            for (int v = w - 1; v > 0 && v >= w - 21; v--)
                dp[w] = min(dp[w], dp[v] + lcm(v, w));
        }
        System.out.println(dp[N]);
    }

    long min(long a, long b) { return a < b ? a : b; }

    int lcm(int a, int b) { return a * b / gcd(a, b); }

    int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
}

---

#F 时间显示

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$15$ 分

---

问题描述

  小蓝要和朋友合作开发一个时间显示的网站。在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 $1970$ 年 $1$ 月 1 日 $00:00:00$ 到当前时刻经过的毫秒数。
  现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需显示出时分秒即可，毫秒也不用显示，直接舍去即可。
  给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

---

输入格式

  输入一行包含一个整数，表示时间。

---

输出格式

  输出时分秒表示的当前时间，格式形如 $HH$:$MM$:$SS$，其中 $HH$ 表示时，值为 $0$ 到 $23$，$MM$ 表示分，值为 $0$ 到 $59$，$SS$ 表示秒，值为 $0$ 到 $59$。时、分、秒不足两位时补前导 $0$。

---

测试样例₁

Input：
46800999

Output：
13:00:00

测试样例₂

Input：
1618708103123

Output：
01:08:23

---

评测用例规模与约定

  对于所有评测用例，给定的时间为不超过 $10^{18}$ 的正整数。

---

Java Win

---

import java.util.Scanner;
import java.time.LocalTime;
import java.time.format.DateTimeFormatter;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        System.out.println(
            LocalTime.MIDNIGHT.
            plusSeconds(
            	new Scanner(System.in).nextLong() / 1000).
            format(DateTimeFormatter.ISO_LOCAL_TIME)
        );
    }
}

---

不依赖 API 的实现

---

import java.util.Scanner;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() {
        long t = new Scanner(System.in).nextLong();
        System.out.printf("%02d:%02d:%02d",
            t / 3600000 % 24, t / 60000 % 60, t / 1000 % 60);
    }
}

  送分。

---

#G 最少砝码

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$20$ 分

---

问题描述

  你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意小于等于 $N$ 的正整数重量。
  那么这套砝码最少需要包含多少个砝码？
  注意砝码可以放在天平两边。

---

输入格式

  输入包含一个正整数 $N$。

---

输出格式

  输出一个整数代表答案。

---

测试样例₁

Input：
7

Output：
3

Explanation：
3 个砝码重量是 1、4、6，可以称出 1 至 7 的所有重量。
1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
少于 3 个砝码不可能称出 1 至 7 的所有重量。

---

评测用例规模与约定

  对于所有评测用例，$1\le N\le 1000000000$。

---

变种三进制

---

  不知道怎么取标题，也算是个规律题，

  这不是纯纯的恶心人吗。

---

  一个集合中包含 $n$ 个数，任取若干数可以加减出任意小于等于 $N$ 的正整数。

  首先要考虑怎么去满足题目要求的性质，

  设第 $i$ 个砝码的重量为 $w_i$，原集合 A N = { w 1 , w 2 , ⋯   , w n } A_{N} = \{w_{1},w_{2},\cdots,w_{n}\} AN​={w1​,w2​,⋯,wn​}。

  要满足题意首先要有 $sum(A)\ge N$，

  设我们知道了 $A_{\lfloor N/3\rfloor }$ 的方案，那么我们就能在这个方案里加入一个 $2\lfloor N/3\rfloor +1$，就能用 $2\lfloor N/3\rfloor +1$ 对 $A_{\lfloor N/3\rfloor }$ 中个若干元素做差表示出 $(\lfloor N/3\rfloor ,2\lfloor N/3\rfloor +1)$，对若干元素求和表示出 $(2\lfloor N/3\rfloor +1,N]$，并入 $A_{\lfloor N/3\rfloor }$ 本身能表示的范围，即能表示出任意小于等于 $N$ 的正整数。

  如果 $A_{\lfloor N/3\rfloor }$ 本身是最优的，那么往里面加入 $K=2\lfloor N/3\rfloor +1$ 的 $A_N$ 也一定是最优的，因为要使得 $K+sum(A_{\lfloor N/3\rfloor })\ge N$，$K$ 必须大于等于 $2\lfloor N/3\rfloor +1$，而当 $K>2\lfloor N/3\rfloor +1$ 时，就无法表示出 $\lfloor N/3\rfloor +1$，

  当然这一切还有个前提条件，那就是 $sum(A_{\lfloor N/3\rfloor })=\lfloor N/3\rfloor$。’

  不过到这里已经足够启发我们去顺推了，

  因为这个问题的边界是显然的，

  当 $N=1$ 时， A 1 = { 1 } A_{1} = \{1\} A1​={1}，

  我们往 $A_1$ 中加入 $2\times sum(A_1)+1$，得到 $A_4$，即

  当 $N=4$ 时， A 4 = { 1 , 3 } A_{4} = \{1,3\} A4​={1,3}，

  当 $N=13$ 时， A 13 = { 1 , 3 , 9 } A_{13} = \{1,3,9\} A13​={1,3,9}，

  $\cdots \cdots$

  当然还存在 $N$ 不在我们找到的最优规律中。

  我们设 $N=5$，

  因为 A 4 = { 1 , 3 } A_{4} = \{1,3\} A4​={1,3} 的最优性，$2$ 个元素至多组成任意小于等于 $4$ 的正整数，

  因为 A 13 = { 1 , 3 , 9 } A_{13} = \{1,3,9\} A13​={1,3,9} 的最优性，$3$ 个元素可以表示任意小于等于 $13$ 的正整数。

  即对 $N=5$ 给出的答案，必须大于 $2$ 小于等于 $3$。

  对于给出任意 $N$ 我们都可以按照这个性质求出答案。

  同时在三进制下来看这个规律：

   { N } = { ( 1 ) 3 , ( 11 ) 3 , ( 11 ) 3 , ⋯   } \{N\} = \{(1)_{3},(11)_{3},(11)_{3},\cdots\} {N}={(1)3​,(11)3​,(11)3​,⋯}

  可以二分，但没有必要。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        long N = new Scanner(System.in).nextLong(), ans = 1;
        for (long pow3 = 1; pow3 < N; pow3 = pow3 * 3 + 1, ans++);
        System.out.println(ans);
    }
}

---

#H 杨辉三角形

时间限制: $5.0$s 内存限制: $512.0$MB 本题总分：$20$ 分

---

  下面的图形是著名的杨辉三角形：
  如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：

  $1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,\cdots$
  给定一个正整数 $N$，请你输出数列中第一次出现 $N$ 是在第几个数？

---

输入格式

  输入一个整数 $N$。

---

输出格式

  输出一个整数代表答案。

---

测试样例₁

Input：
6

Output：
13

---

评测用例规模与约定

  对于 $20$% 的评测用例，$1\le N\le 10$；
  对于所有评测用例，$1\le N\le 1000000000$。

---

  图片高清重置

---

类比单调数列

---

  杨辉三角最外层全部是 $1$。

  第二层则是自然数序列。

  因为杨辉三角是左右对称的，因此我们可以忽略右边(左边的数字总是比右边先出现)，并将数字按层分成若干序列。

  由于序列都是从上置下单调递增的，我们可以在每一个这种序列上，二分查找 $N$ 的位置，特别的，$N=1$ 时直接输出 $1$。

  此外，杨辉三角第 $n$ 行 m $列$

  $=C_{n-1}^{m-1}=\frac{(n-1)!}{(m-1)!(n-m)!}$

  这个数字增长的非常快 $C_{32}^{16}=1166803110>1e9$。

  也就至多在 $14$ 条(除去最外两层)这样的序列中查找 $N$ 的位置，因为序列的单调性不允许 $N$ 的出现。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    int N;

    void run() {
        N = new Scanner(System.in).nextInt();
        if (N == 1) System.out.println(1);
        else {
            long ans = (N + 1L) * N / 2 + 2;
            for (int m = 2; m < 16; m++) {
                int start = m * 2, end = N;
                while (start <= end) {
                    int mid = start + end >> 1;
                    if (C(mid, m) == N) {
                        ans = min(ans, (mid + 1L) * mid / 2 + m + 1);
                        break;
                    } if (C(mid, m) > N) end = mid - 1;
                    else start = mid + 1;
                }
            }
            System.out.println(ans);
        }
    }

    long min(long a, long b) { return a < b ? a : b; }

    long C(int n, int m) {
        long num = 1;
        for (int nm = 1; nm <= m; n--, nm++)
            if ((num = num * n / nm) > N) return num;
        return num;
    }
}

---

#I 左孩子右兄弟

时间限制: $2.0$s 内存限制: $512.0$MB 本题总分：$25$ 分

---

问题描述

  对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。
  如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。
  给定一棵包含 $N$ 个结点的多叉树，结点从 $1$ 至 $N$ 编号，其中 $1$ 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。注：只有根结点这一个结点的树高度为 $0$ 。
  例如如下的多叉树：

  可能有以下 $3$ 种 (这里只列出 $3$ 种，并不是全部) 不同的 “左孩子右兄弟”表示：

  其中最后一种高度最高，为 $4$。

---

输入格式

  输入的第一行包含一个整数 $N$。
  以下 $N-1$ 行，每行包含一个整数，依次表示 $2$ 至 $N$ 号结点的父结点编号。

---

输出格式

  输出一个整数表示答案。

---

测试样例₁

Input：
5
1
1
1
2

Output：
4

---

评测用例规模与约定

  对于 $30$% 的评测用例，$1\le N\le 20$；
  对于所有评测用例，$1\le N\le 100000$。

---

树形 DP

---

  一棵树的高度等于根节点最高子树的高度加一，

  而一棵由左孩子右兄弟表示法得到的二叉树，

  我们可以将最大的子树放在最右边，

  这种策略下，每棵子树的高度为子树个数加最高子树高度。

  显 然 正 确

  于是有状态转移方程： d p ( v ) = c o u n t ( s o n ( v ) ) + m a x { d p ( s o n ( v ) ) } dp(v) = \mathrm{count(son(}v\mathrm{))} + \mathrm{max\{}dp\mathrm{(son(}v\mathrm{))\}} dp(v)=count(son(v))+max{dp(son(v))}

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    List<Integer>[] tree;

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), v;
        tree = new List[n + 1];
        for (int w = 2; w <= n; w++) {
            v = in.readInt();
            if (tree[v] == null)
                tree[v] = new ArrayList();
            tree[v].add(w);
        }
        System.out.println(dp(1));
    }

    int dp(int v) {
        if (tree[v] == null) return 0;
        int max = 0;
        for (int w : tree[v])
            max = Math.max(max, dp(w));
        return tree[v].size() +  max;
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#J 双向排序

时间限制: $5.0$s 内存限制: $512.0$MB 本题总分：$25$ 分

---

问题描述

  给定序列 $(a_1,a_2,\cdot \cdot \cdot ,a_n)=(1,2,\cdot \cdot \cdot ,n)$，即 $a_i=i$。
  小蓝将对这个序列进行 $m$ 次操作，每次可能是将 $a_1,a_2,\cdot \cdot \cdot ,a_{q_i}$ 降序排列，或者将 $a_{q_i},a_{q_{i+1}},\cdot \cdot \cdot ,a_n$ 升序排列。
  请求出操作完成后的序列。

---

输入格式

  输入的第一行包含两个整数 $n,m$，分别表示序列的长度和操作次数。
  接下来 $m$ 行描述对序列的操作，其中第 $i$ 行包含两个整数 $p_i,q_i$ 表示操作类型和参数。当 $p_i=0$ 时，表示将 $a_1,a_2,\cdot \cdot \cdot ,a_{q_i}$ 降序排列；当 $p_i=1$ 时，表示将 $a_{q_i},a_{q_{i+1}},\cdot \cdot \cdot ,a_n$ 升序排列。

---

输出格式

  输出一行，包含 $n$ 个整数，相邻的整数之间使用一个空格分隔，表示操作完成后的序列。

---

测试样例₁

Input：
3 3
0 3
1 2
0 2

Output：
3 1 2

Explanation：
原数列为 (1, 2, 3)。
第 1 步后为 (3, 2, 1)。
第 2 步后为 (3, 1, 2)。
第 3 步后为 (3, 1, 2)。与第 2 步操作后相同，因为前两个数已经是降序了。

---

评测用例规模与约定

  对于 $30$% 的评测用例，$n,m\le 1000$；
  对于 $60$% 的评测用例，$n,m\le 5000$；
  对于所有评测用例，$1\le n,m\le 100000$，$0\le p_i\le 1$，$1\le q_i\le n$；

---

去冗操作

---

  其实看到这个数据规模，五分钟写完 Brute Force，就可以下一道了，$O(mn\log n)$ 就能过 $60$% 的用例，

  多的时间去证明其他程序的正确性可能收益会高点。

  不过，骗分就多骗两个吧。

  对于连续且 $p_i$ 相同操作，在 $p_i=0$ 时只需要做 $q_i$ 最大的操作，在 $p_i=1$ 时只需要做 $q_i$ 最小的操作，如图：

  显然去掉冗余操作后，还是和原操作是等价的，只需要建立一个栈就能在线性时间内完成去冗，并且代码量较少。

  特别的，我可以先将 $(p:1,q:1)$ 压入栈底。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.readInt(), m = in.readInt();
        Deque<Step> deque = new ArrayDeque();
        deque.push(new Step(1, 1));
        while (m-- > 0) {
            int p = in.readInt();
            int q = in.readInt();
            while (deque.size() > 0 && deque.peek().p == p)
                if (p == 0)
                    q = max(q, deque.pop().q);
                else
                    q = min(q, deque.pop().q);
            deque.push(new Step(p, q));
        }
        Integer[] ans = new Integer[n];
        for (int i = 0; i < n; i++)
            ans[i] = i + 1;
        deque.pollLast();
        while (deque.size() > 0) {
            Step step = deque.pollLast();
            if (step.p == 0)
                Arrays.sort(ans, 0, step.q, (a, b)->(b - a));
            else
                Arrays.sort(ans, step.q - 1, n);
        }
        for (int i = 0; i < n; i++) {
            out.print(ans[i]);
            out.print(' ');
        }
        out.flush();
    }

    int max(int a, int b) { return a > b ? a : b; }

    int min(int a, int b) { return a < b ? a : b; }

    class Step {

        int p, q;

        Step(int p, int q) {
            this.p = p;
            this.q = q;
        }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

填数游戏

---

  其实最开始就想直接写到这一步，

  但是我忙的同时又有点闲，就拆开写吧。

  经过上述去冗操作，可以发现，最后需要操作的是一个 $p0\mid 1$ 交替的序列，为了便于读者理解，

  这里将原序列和操作抽象成不等长不同色线段，

  特别的，原序列和 $p=1$ 的操作是一个颜色，因为原序列本就是升序。

  将 $p=0$ 和 $p=1$ 最大操作范围标记出来。

  显然，在 $q$ 不为端点时，每次操作都有段不变的区间。

  图像告诉了我们，如果 $q$ 操作的范围盖过了栈里最近的 $q$，那么不仅这个最近的 $q$，连同栈顶 $q$ 相反的操作都是可以跳过的。

  同时根据这个性质优化后，根据栈内剩余的操作，我们总是能找到一段顺或倒序的不变区间。

  将不变区间填入最终的答案，整个算法就大体完成了。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.readInt(), m = in.readInt(), top;
        Step[] stack = new Step[m + 1];
        for (top = 0; m-- > 0;) {
            int p = in.readInt();
            int q = in.readInt();
            if (p == 0) {
                while (top > 0 && stack[top].p == p) q = max(q, stack[top--].q);
                while (top > 1 && stack[top - 1].q <= q) top -= 2;
                stack[++top] = new Step(p, q);
            } else if (top > 0){
                while (top > 0 && stack[top].p == p) q = min(q, stack[top--].q);
                while (top > 1 && stack[top - 1].q >= q) top -= 2;
                stack[++top] = new Step(p, q);
            }
        }
        int[] ans = new int[n + 1];
        int a = n, l = 0, r = n - 1;
        for (int i = 1; i <= top; i++)
            if (stack[i].p == 0)
                while (r >= stack[i].q && l <= r) ans[r--] = a--;
            else
                while (l + 1 < stack[i].q && l <= r) ans[l++] = a--;
        if ((top & 1) == 1)
            while (l <= r) ans[l++] = a--;
        else
            while (l <= r) ans[r--] = a--;
        for (int i = 0; i < n; i++) {
            out.print(ans[i]);
            out.print(' ');
        }
        out.flush();
    }

    int max(int a, int b) { return a > b ? a : b; }

    int min(int a, int b) { return a < b ? a : b; }

    class Step {

        int p, q;

        Step(int p, int q) {
            this.p = p;
            this.q = q;
        }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

Chtholly Tree

---

  未加限定的珂朵莉树 ($\mathrm{C}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{y}\mathrm{T}\mathrm{r}\mathrm{e}\mathrm{e}$)，就是红黑树上建值域线段树，在随机构造的数据下期望复杂度为 $O(n\log \log n)$，

  但 $\mathrm{J}\mathrm{a}\mathrm{v}\mathrm{a}$ 实现起来非常痛苦，于是 $\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{B}$，改用链表实现，

  其在随机构造的数据下期望复杂度为 $O(n\log n)$。

  珂朵莉树的策略就是将值域相同的区间合并成一个节点，

  对于任意 $[L,R]$ 上的操作，我们都能转换成珂朵莉树 $\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}(\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}(\mathrm{L}),\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}(\mathrm{R}+1))$ 上的操作。

  这里其实是珂朵莉链表而不是树

  举个具体且形象的例子对我来说还是太难了，

  兄弟们自己找篇博客参考一下吧。

  虽然捏个踢烂珂朵莉树的数据很简单，

  但就蓝桥的难度而言，

  出题人见没见过还是个问题。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), m = in.readInt();
        Node[] root = new Node[n + 1];
        int[] P = new int[n + 1];
        Range lower, temp, now;
        lower = now = new Range(0);
        for (int i = 1; i <= n; i++) {
            now = now.next = new Range(i);
            root[i] = build(1, n, i);
        }
        now.next = new Range(n + 1);
        while (m-- > 0) {
            int p = in.readInt();
            int L = in.readInt();
            int R = n;
            if (p == 0) {
                R = L;
                L = 1;
            }
            now = lower;
            while (now.next.L <= L) now = now.next;
            if (L > now.L) {
                root[L] = split(root[now.L], L - now.L, P[now.L]);
                now = now.next = new Range(L, now.next);
            }
            temp = now;
            Node pq = null;
            while (now.L <= R) {
                if (now.next.L > R + 1) root[R + 1] = split(root[now.L], R + 1 - now.L, P[R + 1] = P[now.L]);
                pq = merge(pq, root[now.L]);
                now = now.next;
            }
            if (now.L == R + 1) temp.next = now;
            else temp.next = new Range(R + 1, now);
            root[L] = pq;
            P[L] = p;
        }
        StringBuilder ans = new StringBuilder();
        while ((lower = lower.next).L <= n)
            buildAns(ans, root[lower.L], 1, n, P[lower.L]);
        System.out.println(ans);
    }

    Node split(Node tree, int k, int p) {
        if (tree == null) return null;
        Node split= new Node(0);
        if (p == 0) {
            int K = K(tree.right);
            if (k <= K) {
                if (k != K) split.right = split(tree.right, k, p);
                split.left = tree.left;
                tree.left = null;
            } else split.left = split(tree.left, k - K, p);
        } else {
            int K = K(tree.left);
            if (k <= K) {
                if (k != K) split.left = split(tree.left, k, p);
                split.right = tree.right;
                tree.right = null;
            } else split.right = split(tree.right, k - K, p);
        }
        split.k = tree.k - k;
        tree.k = k;
        return split;
    }

    Node merge(Node tree1, Node tree2) {
        if (tree1 == null) return tree2;
        if (tree2 != null){
            tree1.k += K(tree2);
            tree1.left = merge(tree1.left, tree2.left);
            tree1.right = merge(tree1.right, tree2.right);
        }
        return tree1;
    }

    Node build(int L, int R, int k) {
        if (L == R) return new Node(1);
        Node node = new Node(1);
        int mid = L + R >> 1;
        if (k <= mid) node.left = build(L, mid, k);
        else node.right = build(mid + 1, R, k);
        return node;
    }

    void buildAns(StringBuilder builder, Node root, int L, int R, int p) {
        if (root == null) return;
        if (L == R) builder.append(L).append(' ');
        else {
            int mid = L + R >> 1;
            if (p == 0) {
                buildAns(builder, root.right, mid + 1, R, p);
                buildAns(builder, root.left, L, mid, p);
            } else {
                buildAns(builder, root.left, L, mid, p);
                buildAns(builder, root.right, mid + 1, R, p);
            }
        }
    }

    int K(Node node) { return node == null ? 0 : node.k; }

    class Range {

        int L;

        Range next;

        Range(int L) { this(L, null); }

        Range(int L, Range next) {
            this.L = L;
            this.next = next;
        }
    }

    class Node {

        int k = 1;

        Node left, right;

        Node(int k) { this.k = k; }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) { this.reader = new BufferedReader(new InputStreamReader(in)); }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(this.read()); }
    }
}

---