线段树详解

已于 2022-07-13 09:24:58 修改
阅读量1.8k 收藏 15
点赞数 3
分类专栏： 数据结构与算法 文章标签： java 算法 前端
于 2022-07-12 11:08:26 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_43478694/article/details/125702075
版权

文章目录

1. 线段树概念

线段树（segment tree）是一种基于分治思想的二叉树，它的每个节点都对应一个[L , R ]区间，叶子节点对应的区间L =R 。每一个非叶子节点[L , R ]其左子节点的区间都为[L , (L +R )/2]，右子节点的区间都为[(L +R )/2+1, R ]。[1, 10]区间的线段树如下图所示
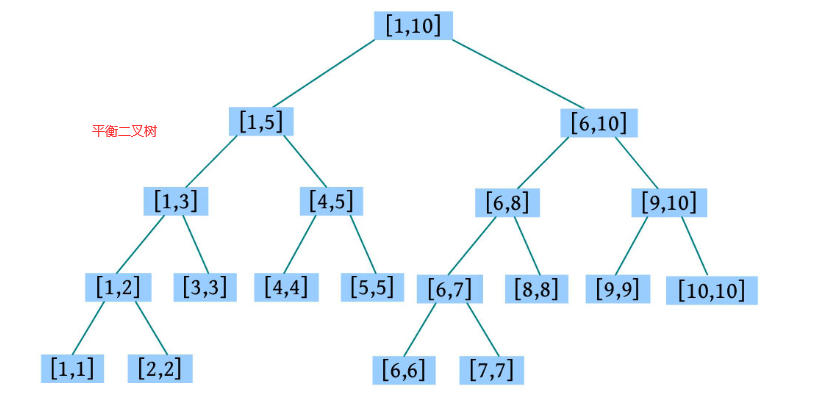
在这里插入图片描述

线段树的存储方式：
线段树除了最后一层，其他层构成一颗满二叉树，因此采用顺序存储方式，用一个数组tree[]存储节点。若一个节点的存储下标为k ，则其左子节点的下标为2k ，其右子节点的下标为2k +1

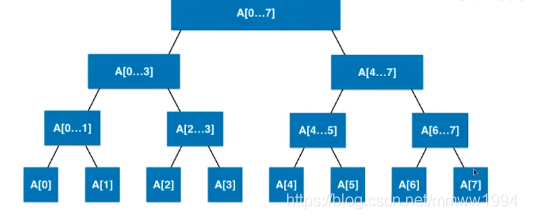
注意：这里使用2k 2k+1作为访问左右孩子，是有空间消耗的，一般而言只有一棵树是完全二叉才可以使用2k 2k+1表示左右孩子，从下图中可以看到，区间[6,6]如果想要被2k进行访问，实际上区间[3,3] [4,4] [5,5]也需要创建相应的空叶子节点
在这里插入图片描述

简单来说，如果区间内的元素个数为 2 k 2^k 2k， 则构造出来的线段树是一棵完全二叉树，否则构造出来的树和上图一样，去掉最后一层后才是满二叉树，此时如果还需要利用完全二叉树的性质，就需要把最后一层不存在的叶子节点也创建出来

元素个数 n = 2 k n=2^k n=2k：
在这里插入图片描述

第0层 2 0 = 1 2^0=1 20=1
第1层 2 1 = 2 2^1=2 21=2
第2层 2 2 = 4. 2^2=4. 22=4.
…
第k层 2 k 2^{k} 2k
总的结点数： 1 + 2 + 4 + . . . . + 2 k = 2 k + 1 − 1 1+2+4+....+2^{k}=2^{k+1}-1 1+2+4+....+2k=2k+1−1
2 k = n 2 k + 1 = 2 n 2^{k}=n \quad 2^{k+1}=2n 2k=n2k+1=2n

因此这种情况空间只需要2n

元素个数 n ! = 2 k n!=2^k n!=2k：

在这里插入图片描述

多出来的元素需要额外一层开来存储，此时结点数在前面的基础上加上最后一层(因为最后一层的最右边有子节点，因此最后一层需要加满节点保证完全二叉树的特性，实际区间节点+额外创建的节点)：
2 k + 1 − 1 + 2 k + 1 = 2 × 2 k + 1 − 1 2^{k+1}-1+2^{k+1}=2 \times 2^{k+1}-1 2k+1−1+2k+1=2×2k+1−1 其中 k = l o g n k=logn k=logn
2 k + 1 = 4 n 2^{k+1}=4n 2k+1=4n
因此这种情况需要4n

综合上面两种情况，最坏情况需要4n;

图片来源：https://blog.csdn.net/mmww1994/article/details/104206072/

2. 线段树的普通形式

1. 创建线段树

采用递归的方法创建线段树，算法步骤如下：

  • 若是叶子节点（l =r ），则节点的最值就是对应位置的元素值
  • 若是非叶子节点，则递归创建左子树和右子树
  • 节点的区间最值等于该节点左右子树最值的最大值
  • 节点的区间和等于该节点左右子树区间和的相加

2. 区间查询

区间查询指查询一个[l , r ]区间的最值或区间和。采用递归的方法进行区间查询的算法步骤如下：

  • 若节点所在的区间被查询区间[l , r ]覆盖，则返回该节点的最值或区间和
  • 判断是在左子树中查询，还是在右子树中查询
  • 返回最值或区间和

3. 点更新
点更新指修改一个元素的值，例如将a [i ]修改为v 。采用递归进行点更新，算法步骤如下：

  • 若i属于当前节点所在区间，更新当前节点区间的最值和区间和
  • 若是非叶子节点，则判断是在左子树中更新还是在右子树中更新，是叶子节点，更新完毕，返回

在这里插入图片描述

package algorithm;

public class SegmentTree {
	int sz;//需要创建的tree数组大小
	int n;//区间长度
	Node[] tree;
	int[] arr;
	public SegmentTree(int[] arr) {
		this.n=arr.length;
		this.arr=arr;
		this.tree=new Node[4*n];
		for(int i=0;i<tree.length;i++) {
			tree[i]=new Node();
		}
		build(0, 0,n-1);
	}
	/*
	 * 创建线段树 节点存储下标为k 节点区间为[left,right]
	 */
	public void build(int k,int left,int right) {
		tree[k].left=left;
		tree[k].right=right;
		if(left==right) {
			tree[k].max=arr[left];
			tree[k].sum=arr[right];
			return;
		}
		int mid=left+(right-left)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		build(lChild, left, mid);
		build(rChild, mid+1, right);
		//更新节点k最大值
		tree[k].max=Math.max(tree[lChild].max,tree[rChild].max);
		//更新节点k区间和
		tree[k].sum=tree[lChild].sum+tree[rChild].sum;
	}
	/*
	 * 更新arr[i]=val
	 */
	public void updateTree(int k, int i,int val) {
		
		if(tree[k].left==tree[k].right&&tree[k].left==i) {
			tree[k].max=val;
			tree[k].sum=val;
			return;
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		if(i<=mid) {
			updateTree(lChild, i, val);//到左子树更新
		}else {
			updateTree(rChild, i, val);//到右子树更新
		}
		//更新节点k最大值
		tree[k].max=Math.max(tree[lChild].max,tree[rChild].max);
		//更新节点k区间和
		tree[k].sum=tree[lChild].sum+tree[rChild].sum;
	}
	/*
	 * 求区间[left,right]中的最大值
	 */
	public int queryMax(int k,int left,int right) {
		//查询区间覆盖该节点区间
		if(tree[k].left>=left&&tree[k].right<=right) {
			return tree[k].max;
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		int maxVal=Integer.MIN_VALUE;
		if(left<=mid) {
			maxVal=Math.max(maxVal,queryMax(lChild, left, right));
		}
		if(right>mid) {
			maxVal=Math.max(maxVal,queryMax(rChild, left, right));
		}
		return maxVal;
	}
	/*
	 * 求区间[left,right]元素和
	 */
	public int querySum(int k,int left,int right) {
		//查询区间覆盖该节点区间
		if(tree[k].left>=left&&tree[k].right<=right) {
			return tree[k].sum;
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		int sum=0;
		if(left<=mid) {
			sum+=querySum(lChild, left, right);
		}
		if(right>mid) {
			sum+=querySum(rChild, left, right);
		}
		return sum;
	}
	
		
	
	public static void main(String[] args) {
		int[] arr= {1,2,3,4,5,6,7,8,9,10};
		SegmentTree sTree=new SegmentTree(arr);
		System.out.println(sTree.queryMax(0, 0, 9));
		System.out.println(sTree.querySum(0, 0, 9));
		System.out.println(sTree.tree[2].max);
		sTree.updateTree(0, 9, 25);
		System.out.println(sTree.queryMax(0, 0, 9));
		System.out.println(sTree.querySum(0, 0, 9));
		System.out.println(sTree.tree[2].max);
	}
	
}
class Node{
	int left,right;//左右孩子编号 2k+1 2k+2 因为从0开始编号
	int sum;//区间和
	int max;//区间最大值
	
}

3. 线段树中的“懒操作”

若对区间的每个点都进行更新，则时间复杂度较高，可以引入懒操作，此时的更新算法如下：

区间更新

  • 若当前节点的区间被查询区间[l , r ]覆盖，则仅对该节点进行更新并做懒标记，表示该节点已被更新，对该节点的子节点暂不更新
  • 判断是在左子树中查询还是在右子树中查询。在查询过程中，若当前节点带有懒标记，则将懒标记下传给子节点（将当前节点的懒标记清除，将子节点更新并做懒标记），继续查询
  • 在返回时更新最值

区间查询

  • 在查询过程中若遇到节点有懒标记，则下传懒标记，继续查询

代码如下：

package algorithm;

public class SegmentTree {
	int sz;//需要创建的tree数组大小
	int n;//区间长度
	Node[] tree;
	int[] arr;
	public SegmentTree(int[] arr) {
		this.n=arr.length;
		this.arr=arr;
		this.tree=new Node[4*n];
		for(int i=0;i<tree.length;i++) {
			tree[i]=new Node();
		}
		build(0, 0,n-1);
	}
	/*
	 * 创建线段树 节点存储下标为k 节点区间为[left,right]
	 */
	public void build(int k,int left,int right) {
		tree[k].left=left;
		tree[k].right=right;
		if(left==right) {
			tree[k].max=arr[left];
			tree[k].sum=arr[right];
			return;
		}
		int mid=left+(right-left)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		build(lChild, left, mid);
		build(rChild, mid+1, right);
		//更新节点k最大值
		tree[k].max=Math.max(tree[lChild].max,tree[rChild].max);
		//更新节点k区间和
		tree[k].sum=tree[lChild].sum+tree[rChild].sum;
	}
	/*
	 * 将区间[left,right]中的元素都加上delta
	 */
	public void updateTree(int k, int left,int right,int delta) {
		//区间覆盖 递归结束 此时更新该区间节点的delta max sum
		if(tree[k].left>=left&&tree[k].right<=right) {
			tree[k].delta+=delta;//delta是累加
			tree[k].max+=delta;
			tree[k].sum+=(tree[k].right-tree[k].left+1)*delta;
			return;
		}
		if(tree[k].delta!=0) {
			pushDown(k);
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		if(left<=mid) {
			updateTree(lChild, left,right, delta);//到左子树更新
		}
		if(right>mid) {
			updateTree(rChild, left,right, delta);//到右子树更新
		}
		//更新节点k最大值
		tree[k].max=Math.max(tree[lChild].max,tree[rChild].max);
		//更新节点k区间和
		tree[k].sum=tree[lChild].sum+tree[rChild].sum;
	}
	/*
	 * 求区间[left,right]中的最大值
	 */
	public int queryMax(int k,int left,int right) {
		//查询区间覆盖该节点区间
		if(tree[k].left>=left&&tree[k].right<=right) {
			return tree[k].max;
		}
		if(tree[k].delta!=0) {
			pushDown(k);//懒标记下传
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		int maxVal=Integer.MIN_VALUE;
		if(left<=mid) {
			maxVal=Math.max(maxVal,queryMax(lChild, left, right));
		}
		if(right>mid) {
			maxVal=Math.max(maxVal,queryMax(rChild, left, right));
		}
		return maxVal;
	}
	/*
	 * 求区间[left,right]元素和
	 */
	public int querySum(int k,int left,int right) {
		//查询区间覆盖该节点区间
		if(tree[k].left>=left&&tree[k].right<=right) {
			return tree[k].sum;
		}
		if(tree[k].delta!=0) {
			pushDown(k);//懒标记下传
		}
		int mid=(tree[k].left+tree[k].right)/2;//划分点
		int lChild=2*k+1;//左子节点存储下标
		int rChild=2*k+2;//右子节点存储下标
		int sum=0;
		if(left<=mid) {
			sum+=querySum(lChild, left, right);
		}
		if(right>mid) {
			sum+=querySum(rChild, left, right);
		}
		return sum;
	}
	/*
	 * 向子节点传递懒标记
	 */
	public void pushDown(int k) {
		Node root=tree[k];
		Node lChild=tree[2*k+1];
		Node rChild=tree[2*k+2];
		int delta=tree[k].delta;
		lChild.delta+=root.delta;
		lChild.sum+=(lChild.right-lChild.left+1)*delta;
		lChild.max+=delta;
		root.delta=0;
	}
	
	
	public static void main(String[] args) {
		int[] arr= {1,2,3,4,5,6,7,8,9,10};
		SegmentTree sTree=new SegmentTree(arr);
		System.out.println("修改前：");
		System.out.println(sTree.queryMax(0, 0, 9));
		System.out.println(sTree.querySum(0, 0, 9));
		System.out.println(sTree.tree[1].max);
		sTree.updateTree(0, 0,9,3);//区间0-9中的所有元素加上3
		System.out.println("修改后：");
		System.out.println(sTree.queryMax(0, 0, 9));
		System.out.println(sTree.querySum(0, 0, 9));
		System.out.println(sTree.tree[2].max);
		sTree.updateTree(0, 0,9,4);//区间0-9中的所有元素加上4
		System.out.println("修改后：");
		System.out.println(sTree.queryMax(0, 0, 9));
		System.out.println(sTree.querySum(0, 0, 9));
		System.out.println(sTree.tree[2].max);
	}
	
}
class Node{
	int left,right;//左右孩子编号 2k+1 2k+2 因为从0开始编号
	int sum;//区间和
	int max;//区间最大值
	int delta;//懒标记 表示加上过的值 变化量
	
}

总结：

在没有设置懒标记之前，即使区间覆盖也还是需要更新该区间的子节点，直到遇到区间长度为1的节点，设置懒标记之后，只需要更新区间覆盖的节点，其子节点延迟更新；当需要访问的时候再将懒惰标记下移，继续查询。

4. 线段树之动态开点

当区间范围比较大时，比如[1,1e9], 此时如果再开4倍空间可能会导致内存溢出，但是实际上我们并不需要建=建立一棵完整的线段树，先只建立一个根节点代表整个区间，然后当需要访问的时候再去创建相应的节点，没有访问到的区间就不为其创建相应的节点，如果我们是按照连续段进行查询或插入，最坏情况下仍然会占到4n的空间。每一个节点的左右儿子不是该点编号的两倍和两倍加一，而是现加出来的，比如之前节点k的左子节点为2*k+1, 在动态开点的创建方式中，节点k的左子节点为k+1

package algorithm;

public class SegmentTree {
	int sz;// 需要创建的tree数组大小
	int n;// 区间长度
	Node[] tree;
	int[] arr;
	//N M的值尽量大
	static int N = (int) 1e9 + 10;//N代表值域大小
	int M = 500010, cnt = 0;//M代表查询次数 查询一次最多创建3个节点

	public SegmentTree(int[] arr) {
		this.n = arr.length;
		this.arr = arr;
		this.tree = new Node[M];
	}

	/*
	 * 创建线段树 只创建一个根节点 其他的节点延迟创建
	 */
	public void build() {
		tree[0] = new Node();
		tree[0].left = 0;
		tree[0].right = 0;
		tree[0].delta = 0;
	}

	/*
	 * 将区间[left,right]中的元素都加上delta
	 */
	public void updateTree(int k, int lChild, int rChild, int left, int right, int delta) {

		if (left <= lChild && rChild <= right) {// 区间覆盖 更新当前区间的区间和和最大值
			tree[k].sum += (rChild - lChild + 1) * delta;
			tree[k].max += delta;
			tree[k].delta += delta;
			return;
		}
		lazyCreate(k);// 延迟创建节点k
		pushDown(k, rChild - lChild + 1);// 懒标记下移
		int mid = lChild + (rChild - lChild) / 2;
		if (left <= mid) {
			updateTree(tree[k].left, lChild, mid, left, right, delta);// 更新左子树
		}
		if (right > mid) {
			updateTree(tree[k].right, mid + 1, rChild, left, right, delta);// 更新右子树
		}
		pushUp(k);// 更新区间节点k的sum和max

	}

	public void lazyCreate(int k) {
		if (tree[k] == null) {// 编号为k的节点没有被创建
			tree[k] = new Node();
		}
		if (tree[k].left == 0) {// 左子节点没有被创建
			tree[k].left = ++cnt;// 左子节点编号
			tree[tree[k].left] = new Node();
		}
		if (tree[k].right == 0) {
			tree[k].right = ++cnt;// 右子节点编号
			tree[tree[k].right] = new Node();
		}
	}

	public void pushDown(int k, int len) {
		if (tree[k].delta == 0) {// delta=0不要进行懒标记下移
			return;
		}
		// 对区间进行加」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
		tree[tree[k].left].delta += tree[k].delta;
		tree[tree[k].right].delta += tree[k].delta;
		tree[tree[k].left].sum += (len - len / 2) * tree[k].delta;
		tree[tree[k].right].sum += (len / 2) * tree[k].delta;
		tree[tree[k].left].max += tree[k].delta;
		tree[tree[k].right].max += tree[k].delta;
		tree[k].delta = 0;// 父节点k的懒标记清除
	}

	/*
	 * 更新节点k的sum和max
	 */
	public void pushUp(int k) {
		tree[k].sum = tree[tree[k].left].sum + tree[tree[k].right].sum;
		tree[k].max = Math.max(tree[tree[k].left].max, tree[tree[k].right].max);
	}

	/*
	 * 求区间[left,right]中的最大值
	 */
	public int queryMax(int k, int lChild, int rChild, int left, int right) {
		if (left <= lChild && rChild <= right) {
			return tree[k].max;
		}
		lazyCreate(k);
		pushDown(k, rChild - lChild + 1);
		int mid = lChild + (rChild - lChild) / 2;
		int maxVal = Integer.MIN_VALUE;
		if (left <= mid) {
			maxVal = Math.max(maxVal, queryMax(tree[k].left, lChild, mid, left, right));
		}
		if (right > mid) {
			maxVal = Math.max(maxVal, queryMax(tree[k].right, mid + 1, rChild, left, right));
		}
		return maxVal;

	}

	/*
	 * 求区间[left,right]元素和
	 */
	public int querySum(int k, int lChild, int rChild, int left, int right) {
		if (left <= lChild && rChild <= right) {
			return tree[k].sum;
		}
		lazyCreate(k);
		pushDown(k, rChild - lChild + 1);
		int mid = lChild + (rChild - lChild) / 2;
		int sum = 0;
		if (left <= mid) {
			sum += querySum(tree[k].left, lChild, mid, left, right);
		}
		if (right > mid) {
			sum += querySum(tree[k].right, mid + 1, rChild, left, right);
		}
		return sum;

	}

	public static void main(String[] args) {
		int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
		SegmentTree sTree = new SegmentTree(arr);
		// 更新和查询时设置区间[lChild,rChild] 不被区间[left,right] 覆盖 否则无法延迟创建节点 导致空指针异常
		// N是一个比较大的值
		sTree.updateTree(0, 0, N, 0, arr.length - 1, 5);// 区间[1,9]值为5
		System.out.println("区间和查询:" + sTree.querySum(0, 0, N, 1, arr.length - 1));// [1,9]区间和为45
		System.out.println("最大值查询:" + sTree.queryMax(0, 0, N, 1, arr.length - 1));// [1,9]区间最大值为5
		System.out.println();
		sTree.updateTree(0, 0, N, 0, 3, 15);// [0,3]区间+15-->15 20 20 20 5 5 5 5 5 5
		System.out.println("区间和查询:" + sTree.querySum(0, 0, N, 1, arr.length - 1));// [1,9]区间和为90
		System.out.println("最大值查询:" + sTree.queryMax(0, 0, N, 1, arr.length - 1));// [1,9]区间最大值为20
		System.out.println();
	}

}

class Node {
	int left, right;// 左右孩子编号 2k+1 2k+2 因为从0开始编号
	int sum;// 区间和
	int max;// 区间最大值
	int delta;// 懒标记 表示加上过的值 变化量

}

再贴一个动态开点的指针做法，即不提前创建tree[]数组，参考代码出处

    /**
     * 线段树的结点
     */
    static class Node {
        //左范围
        private int left;
        //右范围
        private int right;
        //区间和
        private int value;
        //懒标记
        private int lazy;
        //左子树和右子树
        Node leftChild, rightChild;

        public Node(int leftX, int rightX) {
            this.left = leftX;
            this.right = rightX;
        }
    }

    private Node root;


    /**
     * 区间更新
     *
     * @param root  树的根
     * @param left  左边界
     * @param right 有边界
     * @param value 更新值
     */
    public void update(Node root, int left, int right, int value) {
        //不在范围内 直接返回
        if (root.left > right || root.right < left) {
            return;
        }
        //修改的区间包含当前结点
        if (root.left >= left && root.right <= right) {
            root.lazy = value;
            root.value = (root.right - root.left + 1) * value;
        } else {
            //动态开点
            lazyCreate(root);
            //下传lazy
            pushDown(root);
            //更新左子树
            update(root.leftChild, left, right, value);
            //更新右子树
            update(root.rightChild, left, right, value);
            //上传结果
            pushUp(root);
        }
    }

    public int query(Node root, int left, int right) {
        if (left <= root.left && root.right <= right) {
            return root.value;
        }
        lazyCreate(root);
        pushDown(root);
        int mid = root.left + (root.right - root.left) / 2;
        if (right <= mid) {
            return query(root.leftChild, left, right);
        } else if (left > mid) {
            return query(root.rightChild, left, right);
        } else {
            return query(root.leftChild, left, mid) + query(root.rightChild, mid + 1, right);
        }
    }

    /**
     * 创建左右子树
     *
     * @param root
     */
    public void lazyCreate(Node root) {
        if (root.leftChild == null) {
            root.leftChild = new Node(root.left, root.left + (root.right - root.left) / 2);
        }
        if (root.rightChild == null) {
            root.rightChild = new Node(root.left + (root.right - root.left) / 2 + 1, root.right);
        }
    }

    /**
     * 下传lazy
     *
     * @param root
     */
    public void pushDown(Node root) {
        if (root.lazy == 0) {
            return;
        }
        int value = root.lazy;
        root.leftChild.lazy = value;
        root.rightChild.lazy = value;
        root.leftChild.value += (root.leftChild.right - root.leftChild.left + 1) * value;
        root.rightChild.value += (root.rightChild.right - root.rightChild.left + 1) * value;
        root.lazy = 0;
    }

    /**
     * 上传结果
     *
     * @param root
     */
    public void pushUp(Node root) {
        root.value = root.leftChild.value + root.rightChild.value;
    }

    public MyCalendar() {
        root = new Node(0, (int) 1e9);
    }

    public boolean book(int start, int end) {
        int query = query(root, start, end - 1);
        if (query > 0) {
            return false;
        }
        update(root, start, end - 1, 1);
        return true;
    }
CodePanda@GPF
关注
  • 3
    点赞
  • 踩
  • 15
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 1
    评论
专栏目录
关于线段树
Tw_light的博客
05-18 227
线段树(Segment Tree) 线段树可在O(log n)的时间复杂度内实现单点修改、区间修改、区间查询（区间和，区间最大/最小值）等操作 线段树的结构和建树 线段树建树 区间查询（区间求和） 单点修改 线段树把一整个线段划分成一个树形结构，将每个长度不为1的区间划分成左右两个区间递归求解。 设用数组st[ ] 来保存线段树, st[i] 为线段树上编号为i的结点的值 （st[i]表示编号为i的结点所管理的区间的和） st[1] = a[1] + a[2] + a[3] + a[4] st[2]
超详解线段树(浅显易懂,几乎涵盖所有线段树类型讲解,匠心之作,图文并茂)
weq2011的博客
01-29 1万+
超详解线段树(浅显易懂,几乎涵盖所有线段树类型讲解,匠心之作,图文并茂)
线段树详解 （原理，实现与应用）
热门推荐
岩之痕
09-09 14万+
线段树详解 By 岩之痕 一：综述 线段树是一种可以快速进行区间修改和区间查询的数据结构。点修改，区间修改和区间查询的复杂度都是O(log2(n)) 并且，线段树可以维护很多种类的信息。说到线段树就不得不提一下树状数组，树状数组维护的信息必须满足区间减法，因为树状数组只是维护1到X的信息，通过相减来得到区间信息，代码简单而且速度快，占用空间又少于线段树，所以一般情况下可以用树状数组的地方就
算法课程笔记——线段树动态开点
最新发布
2302_79123319的博客
06-13 433
算法课程笔记——线段树动态开点。
算法数据结构——线段树（Segment Tree）精讲及python实现
白话机器学习
06-05 3280
线段树（Segment Tree）：一种基于分治思想的二叉树，用于在区间上进行信息统计。它的每一个节点都对应一个区间leftright通常是整数。每一个叶子节点表示了一个单位区间（长度为1），叶子节点对应区间上。每一个非叶子节点的左子节点表示的区间都为，右子节点表示的的区间都为。线段树是一棵平衡二叉树，树上的每个节点维护一个区间。根节点维护的是整个区间，每个节点维护的是父亲节点的区间二等分之后的其中一个子区间。当有n。
线段树（从入门到进阶）
hahahahahaha5的博客
10-31 2044
首先，讲解线段树之前，应该了解到线段树应该是一种工具，可以将一些对于区间（或者线段）的修改、维护，从O(N)的时间复杂度变成O（logN）。 一.线段树概念引入 线段树是一种二叉树，也就是对于一个线段，我们会用一个二叉树来表示。比如说一个长度为5的线段，我们可以表示成这样： 这代表着如果你要表示线段的和，那么最上面的根节点权值就等于两个儿子节点的权值之和。 那么就可以得到：节点i的权值 = i节点的左儿子权值 + i节点的右儿子权值 二.简单线段树 三.区间+/-修改与区间查询 四.区间乘除修改与查询
线段树详解（含代码实现经过测试）
qq_56999918的博客
02-11 1785
1.线段树介绍 什么是线段树？线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。[1] 对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。 使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。--..
线段树详解 (原理,实现与应用)
03-09
线段树详解 (原理,实现与应用) 线段树是一棵完美二叉树,树上的每个节点都维护一个区间。根维护的是整个区间,每个节点维护的是父亲的区间二等分后的其中一个子区间。
线段树详解(C++版).pdf
11-04
。。。
线段树详解(C++版) (2).pdf
11-04
。。。
pascal区间线段树
11-18
**Pascal 区间线段树详解** 线段树（Segment Tree）是一种数据结构，用于高效地处理数组或序列上的区间查询与修改操作。在Pascal编程语言中，我们可以使用记录（Record）类型来实现一个区间线段树。以下是基于给定...
线段树详解（附图解，模板及经典例题分析）
qq_63786973的博客
10-31 2746
线段树是一种常用来维护区间信息的数据结构 ​ 可以在 O(logn) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间的最大值，求区间的最小值）等操作 ​ 如下图所示，线段树是建立在区间基础上的树，树的每个节点都代表着一段区间【L，R】
线段树（SegmentTree）
数据工匠记
06-11 668
线段树（segment tree）顾名思义， 是用来存放给定区间（segment or interval）内对应信息的一种数据结构。
线段树模板(史上最简单易懂的数据结构)
weixin_54442315的博客
04-19 2941
什么是线段树？ 线段树言下之意就是将线段分解为一颗树，并且这颗树是一颗二叉树，树上的每一个节点都具有某些性质。 线段树有什么用？ 线段树主要能够在O(logn)的时间复杂度上解决区间上的问题。 题目引入：AcWing243.一个简单的整数问题2 本题目就是很简单的线段树的板子题，可以用来当做模板来使用。 线段树的几个重要操作： 1.tree[]数组的建立： struct node{ int l;//表示左端点 int r;//表示右端点 int v;//表示区间内的...
线段树的四种模板
lhm的博客
07-20 3877
第一种模板只适合单点修改的题目，每次修改都传递到树的子节点。对于区间修改则不合适，同时，由于数组大小事先申明好，其点数也有上限。为了解决数据量的问题，这里提供了动态开点，解除了每个树的元素都占一个固定坑位的限制。但是仍然有限制，点数不可以随便加，有上限。和第一套模板相比，增加了区间修改的功能。但是点数仍然有上限，数据量顶多十万，再往上就不能适用了。点数无限制，需要的时候申请，但是效率会很低。...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

CodePanda@GPF

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值