09、Non-Black-Box ZK(Barak‘s protocol)--Alon Rosen-CSDN博客

本文链接：https://blog.csdn.net/qq_43479839/article/details/113349323

本文概述了在第九届BIU密码学冬令营中，Alon Rosen博士讲解的Non-Black-Box ZK（Barak's protocol）如何为NP问题提供常数轮的零知识论证。核心概念包括使用验证者代码作为伪见证、非交互式证明系统（如WIPOK和WIAOK）、碰撞抵抗哈希函数和通用语言Lu的应用。文章详细解释了如何构造零知识论证、保证完整性和soundness，以及解决技术挑战如时间复杂性和承诺固定长度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

09、Non-Black-Box ZK(Barak’s protocol)–Alon Rosen

这篇博客，是第九届BIU密码学冬令营上的第10篇内容；整个目录链接如下：

目录@xyi

09、Non-Black-Box ZK(Barak's protocol)--Alon Rosen

9.1 the Goal

其中V抛硬币，结果是随机的
要注意Argument 和Proof的一些区别

在这里插入图片描述

9.2 Non-BB Argument for NP

为什么对于NP问题需要Non-BB论证的？

没有L∈BPP会有一个黑盒协议满足：常数轮、有可忽略的可靠性【即保证验证者不会被不诚实的证明者欺骗】，public-coin
所以我们需要一个非黑盒的模拟器，
一方面：∀V∃S比∃S ∀V更容易【大概的意思是说：去证明每一个验证者都存在一个模拟器比证明存在一个模拟器对于所有验证者成立要简单；因为在后者的S是一个通用的模拟器；】【但是好像是说原本这个地方就有错，我也不是很清楚】
视频原话： Because proving that for every verifier there exists a simulator should be easier than trivial and universal simulator that works for all very fast.
另一方面：我们从哪里开始？1、V的逆转是很难得；2、给出关键的点：我们不需要去进行V的逆向工程；3、只需要证明对于S来说拥有V*的代码就可以了

在这里插入图片描述

9.2.1 Idea【使用一个验证者的代码作为一个“假的”witness】

想法：使用一个验证者的代码作为一个“假的”witness。

在真实的证明中，这个代码是验证者V中随机的消息。
在模拟器中，这个代码是V*的“下一次消息的函数”。
因为在真正的交互中P不能访问到V的随机消息。所以这不会伤害可靠性。在模拟器S中，则总是能使得验证者接受，因为S以V*的代码作为输入。

在这里插入图片描述

9.3 Collision-Resistant Hash Functions

在这里插入图片描述

9.4 Constant-Round ZK Arguments for NP

在这里插入图片描述

9.4.1 the Basic Idea

其中：WIAOK和WIPOK在我之前的博客中有详细的介绍，如下：
https://blog.csdn.net/qq_43479839/article/details/113346611
下面有俩个定理，之后给出定理所描述的内容：

1、假设一个非交互式在统计上绑定的承诺，每一个L∈NP有一个三轮的witness-indistinguishable proof 【WIPOK 【witness不可区分性知识证明】：witness-indistinguishable proof of Knowledge 】
2、假设一个俩轮的统计上隐藏的承诺，每一个L∈NP有一个4轮的witness-independent argument of Knowledge 【WIAOK：witness独立性知识论证】
我们会使用WIPOK和WIAOK这俩个工具去构建：一个5轮的对于NPSZK的知识的论证、和一个常数轮的认证方案。

在这里这个r就是上面提到的那个random tape。
P发送垃圾字符串“00…0”的的承诺给V
之后这个验证者发送一个随机的字符串r给P。
然后证明者P和验证者V都参与到对witness的独立性的知识论证(WIAOK)中,
这个黄色的部分就是我们要证明的式子，其中有一个关键的点，就是这个c不在是之前那个000，而是对于program
π的承诺，满足π(z)=r的式子
我们已经事先准备好了一个程序π来预测你的第二个结束位r的信息。
NTIME(t(n))
statement：是在一个不确定的时间内的，意思是说：如果在π(z)=r那里有一个固定的多项式这会是一个NP声明，但是这个程序π不是有一个固定的多项式，所以我们必须容纳任意t(n),它是多项式。
下面Intuition：中的显而易见

在这里插入图片描述

9.4.2 Completeness

为什么这件事会在高层次上完成：

它的完成是因为我们使用witness去证明，我们可以用w来WIAOK中的第一项使得Verifier接受，【第二步已经不用管了】

9.4.3 Soundness

前提假设：现在假设我们想继续这个问题，当我们有一个P*的证明者他想在论证中作弊；为了去验证可靠性。
即对比上面的，×掉的部分不在满足，所以P肯定会被分配给一个预测下一条信息的程序，即在WIAOK中的第二步去执行。c是对程序π的承诺，所以在WIAOK开始之前，P就必须去猜测什么样的π会使得π(z)=r。
在任何程序中，对于任何固定的短输入z，我们预测一个很长的字符串r的概率是可忽略的。如果没有指定z的长度，虽然可以攻击，但是一旦z明显比r短就很难预测下一条消息了。

在这里插入图片描述

9.4.3 Zero-Knowledge

根据零知识的证明的定义：会有一个Simulator。

By definition，π(z)=V*©=r;
之后使用V*©去证明，但是由于在这其中由于WIAOK是统计上的不可区分的，所以是不能区分是1还是2证明成功？。

9.5 Observations and Technical Issues

Observation1：模拟器运行在在限制的多项式时间内，
First Technical issue1 :V*…,但是却不是先验约束；我们需要考虑，我们怎样能使用固定长度的承诺；解决方案是，使用一个哈希函数，都hash到一个固定长度k的字符串上，之后再去…
Observation2:只需要证明模拟器知道V*的代码就够了，我们所需要的就是预测下一条信息的能力。
First Technical issue2：t(n)的运行时间不是在多项式时间内，所以NTIME(t(n))关系在WIAOK中不是NP关系。解决方案是：WIAOK解决。。

在这里插入图片描述

9.6 A constant-round ZK Argument【常数轮的ZK论证】

其中，Hash函数h是为了固定承诺的长度，其他没有什么，【其它没什么可说的，就是在9.5中的对第一个问题的解决方案的实现】

在这里插入图片描述

9.7 the Relation R_SIM

由于签名承诺部分有一点点变换，现在对所需要论证的地方，也就是黄色的部分做一点修改，

给出了一个关系SIM:
1、z的长度要比r短
2、s是一个随机值。
3、同上不变

在这里插入图片描述

9.8 the Universal Language Lu

定义一种通用的语言：。。【为了解决NTIME(t(n))关系在WIAOK中不是NP关系】
语言Lu的实例是y=(M,x,t)满足下面的条件。
【其中M：machine，是一种机器，并在一定时间范围内输入到机器上，】你可以把它想象成一个Verifier M。
我们希望，NP中的每一种语言都可以简化为这种通用语言Lu。
…
更重要的是，一个对于Lu的证明系统能解决NTIME(n^w(1)) statement。

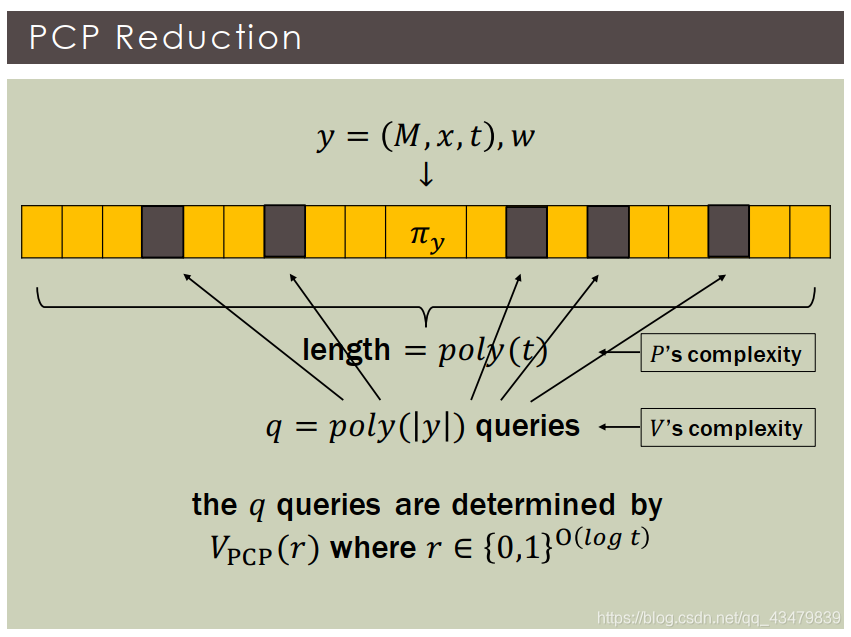
在这里插入图片描述