Segment 3：Introduction Number Theory——Modular e’th roots：

Segment 3：Introduction Number Theory——Modular e’th roots：链接

这是整个数论简介的内容，下面是这个的主目录如下，其链接为：https://blog.csdn.net/qq_43479839/article/details/119079620

在Segment1中，我们讨论了如何解模线性方程【Solving modular linear equations】；更一般地，我们要看如何计算模e次方根【modular e’th roots】

3.1 Modular e’th roots【模e次方根】：最开始都是模质数

1》 我们现在知道如何去解线性方程了；通过适用求逆的Euclid欧几里得算法来计算一个数的逆，如何在乘以-b；

2》 问题是：解质数模多项式方程【polynomials modulo primes】，即解Zp（mod p）中的多项式方程；例如在Zp上解下面的多项式；

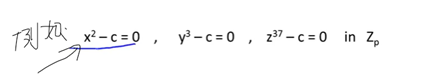
1、Modular e’th roots【模e方根的定义】

1>那么我们固定质数p，我们说c是Zp中的某元素，我们说在Zp中，X满足X的e次方等于c（Xe = c）；我们就说x是c的e次方根；
例如：如下在Z11中6的3次方等于7，故6是7的3次方根；

但是值得注意的是：这些e次方根不一定总是存在；例如：

下一个问题是：什么时候这些e次方根存在？当我们知道它们存在时，我们能否有效地计算它们？

2、 the easy case【什么时候这些e次方根存在？当我们知道它们存在时，我们能否有效地计算它们？】

the easy case：当我们想计算某个数的e次方根时，正好有e与p-1互质；
在Zp上；这时c的e次方始终存在；并且有一个非常容易的算法；如下有证明：
证明1：当e与p-1互质时，对Zp中的所有c，c的e次方根总是存在的；证明2：c的e次方等于cd in Zp

总得来说：就是当e与p-1互质的时候，c的e次方根总是存在，并且容易计算；

3、 一个经典的例子是：e=2；求其平方根的例子（当e与p-1不互质的时候）[2次方–>平方根；3次方->立方根；4次方->4次方根]

1> 假设p是一个奇质数，事实上，我们关注的一直是奇质数；

2> 即上张ppt里面求e的次方根的方法在这里并不适用；我们想计算奇质数模(modulo an odd prime);那么当我们工作在奇质数模下，x—>x2平方函数实际上是2到1函数（本质上，这个平方函数也是一个群同态），因为它把x和-x映射到了同一个值x^2。【其中这个-x表示的是x的加法的逆运算x+y mod n =0】
3> 一个从2到1函数的简单例子：

4> 故有上面的例子可以看到：1,4,9,5,3都是有平方根的；例如4的平方根时2和9；即事实上，除上面的5个元素外，在Z11里的其他元素都没有平方根。
5> 因此引出了一个定义二次剩余【quadratic residue(Q.R.)】：如果x它在Zp中有一个平方根，则我们称x为一个二次剩余；如果它在Zp中没有平方根，我们就称它为二次非剩余【non quadratic residue】；例如4模11是一个二次剩余；9也是二次剩余；

6> 那么对于一个奇质数p，Z_p中的二次剩余一共有多少个？the # of Q.R. in Z_p is (p-1)/2+1;【这其中的加1是因为在Zp中还有一个元素0也是二次剩余的，0总是二次剩余的】

4、用Euler’s theorem欧拉定理判断x是否平方根？

1> Thm：他提出了一个非常清楚的测试这些元素是否是二次剩余的表示，如下

2> 我们来看一个Z11的简单例子：下面计算了所有Z11里元素的5次幂；

如上图可以看到X^(p-1)/2的结果始终是1或者-1；那么可以看到1,3，4,9这几个元素是二次剩余；而其他元素不是二次剩余；
3> 值得注意的是：

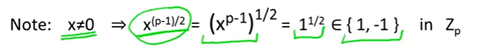
4> 有一个定义Legendre Symbol【勒让德符号】：Zp中所有元素的勒让德符号不是1就是-1；
【欧拉定理很好，但是有一个缺点它并不是构造性的定理】，如果我们想计算一个二次剩余的平方根，证明也是基于存在性依据的；那么它只证明了平方根存在，但是并没有展示如何计算我们想要的平方根，

5、如何计算质数模（modulo p）的平方根

1> 第一种情况是：假设p=3 mod 4;
2> 给一个简单公式用于很容易的计算平方根；如下；因为c的某次幂比次方根容易计算一些。

为什么可以直接用这个公式：给出证明如下：

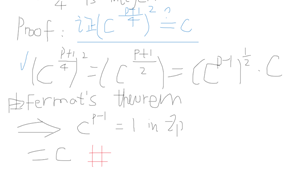
3> 当p=1(mod p)；上面的这个公式就不成立了，只用指数(p+1)/4，它不在是整数；但是实际上当p=1 mod 4时，我们也可以计算平方根，尽管要困难一些，我们没有确定性的算法来计算。我们必须使用一个随机算法来找；我想我应该提到，如果有人能证明扩展的黎曼猜想，一个更深层的解析数论里的猜想，

计算平方根的运行时间是logp的立方

3.2 Solving quadratic equations mod p【讨论解模p的二次方程】：因为我们已经知道怎么计算平方根（square roots）了

1> 假设给一个二次方程，让找到在Zp中的二次方程的解

2> 使用Eulid算法计算2a的逆

3> 先用欧拉定理看b2-4ac的平方根是否存在；也就是看这个元素在(Zp)*上是否是二次剩余，如下

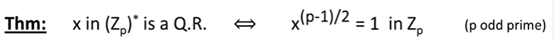
如果有，就使用计算平方根的这个引理来计算它；

3.3 Computing e’th roots mod N(N is composite number)【模合数】在模合数下面计算e次方根

1> 什么时候模N的e次方根存在？如果我们知道它存在我们怎么计算它？我们只知道，计算合数模的e次方根与分解合数【the factorization of composite】一样困难；现在对于一个普通的数e,不知道是否是最优的，但是我们有最好的算法来计算模N的e次方根，需要我们分解这个模，那么实际上每个质数因数的e次方根是容易计算的；我们可以组合所有的这些e次方根来得到合数模N的e次方根；