【LeetCode 面试经典150题】105. Construct Binary Tree from Preorder and Inorder Traversal 从前序和中序构造二叉树

原创 于 2024-01-17 14:50:43 发布 · 444 阅读 · 7 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#leetcode #面试 #算法

105. Construct Binary Tree from Preorder and Inorder Traversal

题目大意

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

中文释义

给定两个整数数组 preorder 和 inorder，其中 preorder 是二叉树的前序遍历，而 inorder 是同一棵树的中序遍历，根据这两个数组构造并返回这棵二叉树。

示例

示例 1:

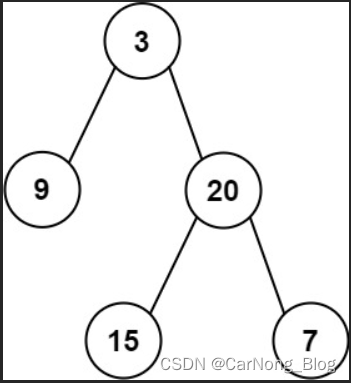
在这里插入图片描述

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出:[-1]

限制条件

  • preorder 的长度范围为 1 <= preorder.length <= 3000。
  • inorder.length == preorder.length。
  • -3000 <= preorder[i], inorder[i] <= 3000。
  • preorder 和 inorder 包含唯一值。
  • inorder 中的每个值也出现在 preorder 中。
  • preorder 保证是树的前序遍历。
  • inorder 保证是树的中序遍历。

解题思路

方法

该方法通过结合前序遍历和中序遍历的数组，构造出原始的二叉树。

  1. 存储遍历结果：

    • 使用两个向量 pre_order 和 in_order 来存储前序遍历和中序遍历的结果。

  2. 创建哈希映射：

    • 使用一个哈希表
最低0.47元/天 解锁文章
C++版-剑指offer 面试题6：重建二叉树(Leetcode105. Construct Binary Tree from Preorder and Inorder Traversal) 解题报告
极客学长Bravo | 突破信息差 | 副业生财有术
04-23 3458
剑指offer 重建二叉树 参与人数：5246  时间限制：1秒  空间限制：32768K 题目描述 输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。 分析
LeetCode105——从前序与中序遍历序列构造二叉树
清风阁
11-17 996
我的LeetCode代码仓：https://github.com/617076674/LeetCode 原题链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/ 题目描述： 知识点：根据前序与中序遍历重建二叉树 思路：前序遍历决...
Construct Binary Tree from Preorder and Inorder Traversal
不积跬步无以至千里
05-04 211
根据前序和中序序列构建一颗二叉树。
105.construct binary tree from preorder and inorder traversal从前序和与中序遍历序列构造二叉树【LeetCode单题讲解系列】
08-31
105.construct_binary_tree_from_preorder_and_inorder_traversal从前序
105. 从前序与中序遍历序列构造二叉树（中等 二叉树 dfs 哈希表 二叉树）
weixin_43942435的博客
07-01 680
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。示例 1:输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7] 示例 2:输入: preorder = [-1], inorder = [-1] 输出: [-1]提示:1 ...
LeetCode Construct Binary Tree from Preorder and Inorder Traversal
DRFish
02-17 1565
通过一棵二叉树的前序和中序排列来得出它的树形结构。
LeetCode——Construct Binary Tree from Preorder and Inorder Traversal
三分地
09-14 2217
Given preorder and inorder traversal of a tree, construct the binary tree. Note: You may assume that duplicates do not exist in the tree. 原题链接：https://oj.leetcode.com/problems/construct-binary-
105. Construct Binary Tree from Preorder and Inorder Traversal
GGGGITFKBJG的主页
12-30 131
105. 从前序与中序遍历序列构造二叉树 根据一棵树的前序遍历与中序遍历构造二叉树。 注意: 你可以假设树中没有重复的元素。 例如，给出 前序遍历 preorder =[3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树： 3 / \ 9 20 / \ 15 7 解法一： //时间复杂度O(n), 空...
LeetCode105—Construct Binary Tree from Preorder and Inorder Traversal
上善若水
03-29 782
LeetCode105—Construct Binary Tree from Preorder and Inorder Traversal
C实现根据二叉树的前序遍历与中序遍历构建二叉树
最新发布
03-25
### 如何用 C 语言通过前序遍历和中序遍历来构建二叉树 在 LeetCode 的题目 **105. Construct Binary Tree from Preorder and Inorder Traversal** 中，目标是从给定的前序遍历 (`preorder`) 和中序遍历 (`inorder`) 构建一棵唯一的二叉树。以下是基于此问题的解决方案。 #### 方法概述 为了完成这一任务，可以采用递归的方法解决该问题。核心思路如下： - 前序遍历的第一个元素总是当前子树的根节点。 - 利用这个根节点，在中序遍历序列中找到其位置 `index`，从而将中序遍历划分为左子树部分（位于索引左侧的部分）和右子树部分（位于索引右侧的部分）。 - 对于每棵子树，重复上述过程直至处理完毕所有节点。 这种方法的时间复杂度为 O(n)，其中 n 是节点的数量[^3]。 #### 数据结构定义 首先需要定义一个表示二叉树节点的数据结构： ```c // 定义二叉树节点结构体 struct TreeNode { int val; struct TreeNode* left; struct TreeNode* right; }; ``` #### 实现代码 下面是完整的 C 语言实现代码： ```c #include <stdio.h> #include <stdlib> // 查找函数：用于在 inorder 数组中定位指定值的位置 int findIndex(int* inorder, int start, int end, int value) { for (int i = start; i <= end; ++i) { if (inorder[i] == value) return i; } return -1; // 如果未找到则返回错误码 } // 辅助递归函数 struct TreeNode* buildTreeHelper( int* preorder, int preStart, int preEnd, int* inorder, int inStart, int inEnd ) { if (preStart > preEnd || inStart > inEnd) return NULL; // 创建新节点并初始化 struct TreeNode* root = malloc(sizeof(struct TreeNode)); root->val = preorder[preStart]; // 在 inorder 数组中寻找根节点的位置 int index = findIndex(inorder, inStart, inEnd, preorder[preStart]); // 计算左子树长度 int leftSize = index - inStart; // 递归构造左右子树 root->left = buildTreeHelper(preorder, preStart + 1, preStart + leftSize, inorder, inStart, index - 1); root->right = buildTreeHelper(preorder, preStart + leftSize + 1, preEnd, inorder, index + 1, inEnd); return root; } // 主调用接口 struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize) { if (!preorder || !inorder || preorderSize != inorderSize) return NULL; return buildTreeHelper(preorder, 0, preorderSize - 1, inorder, 0, inorderSize - 1); } ``` #### 复杂度分析 - 时间复杂度：O(n)[^3]，因为每个节点仅被访问一次。 - 空间复杂度：取决于递归栈的最大深度，最坏情况下可能达到 O(n)。 #### 测试案例 假设输入数据如下： ```plaintext Preorder: [3,9,20,15,7] Inorder : [9,3,15,20,7] ``` 可以通过以下方式测试程序： ```c void printTree(struct TreeNode* node) { if (node == NULL) return; printf("%d ", node->val); printTree(node->left); printTree(node->right); } int main() { int preorder[] = {3, 9, 20, 15, 7}; int inorder[] = {9, 3, 15, 20, 7}; int size = sizeof(preorder)/sizeof(preorder[0]); struct TreeNode* root = buildTree(preorder, size, inorder, size); printTree(root); // 输出应为原前序遍历顺序 return 0; } ``` 运行结果将是 `[3 9 20 15 7]`，这表明重建后的二叉树与原始一致[^4]。 ---
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值