820数据结构（4）树

考纲

1. 树与森林的基本概念
2. 树与森林的存储结构及遍历
3. 二叉树的定义及 6 大性质
4. 二叉树的顺序储存与链式储存结构
5. 二叉树的先序、中序、后序三种遍历方式的关系以及实现；层序遍历的实现
6. 线索二叉树的基本概念与构造方法
7. 树与二叉树的应用：二叉排序树；二叉平衡树；哈夫曼树与哈夫曼编码

一、树和森林的基本概念（了解）

1、树

1. 树是n个节点的有限集。当n=0时，称为空树。
2. 树是一种递归的数据结构。
3. 树作为一种逻辑结构，同时也是一种分层结构。
4. 非空树的特性：
   • 有且仅有一个根节点。
   • 没有后继——叶子结点；有后继——分支结点。
   • 除了根节点以外，任何一个结点都有且仅有一个前驱。
   • 每个结点可以有0个或多个后继。
5. 子树：非空树中，n>1时，其余结点可分为m个互不相交的有限集合，其中每个集合本身又是一棵树。
6. 一些属性
   • 路径长度：从上往下经过多少边。
   • 结点的层次（深度）：从上往下数。
   • 结点的高度——从下往上数。
   • 树的高度（深度）——总共多少层。
   • 结点的度——有几个孩子（分支）
   • 树的度——各结点的度的最大值。（叶子结点的度=0）
7. 有序树——从左至右有次序，不能互换；无序树。
8. 树的性质
   • 结点数 = 总度数+1
   • 度为m的树第i层至多有m^(i-1)个结点（i≥1）
   • 高度为h的m叉树至多有(m^k-1)/(m-1)个结点。
   • 高度为h的m叉树至少有h个结点。
   • 高度为h、度为m的树至少有h+m-1个结点。
   • 具有n个结点的m叉树的最小高度为[logm(n(m-1)+1)]

2、森林

1. 森林是m(m≥0)棵互不相交的树的集合。
2. m=0，空森林。
3. 森林与树的转换。
   

二、树与森林（必考，应用简答：1~2#12）

1、存储结构（手动推导）

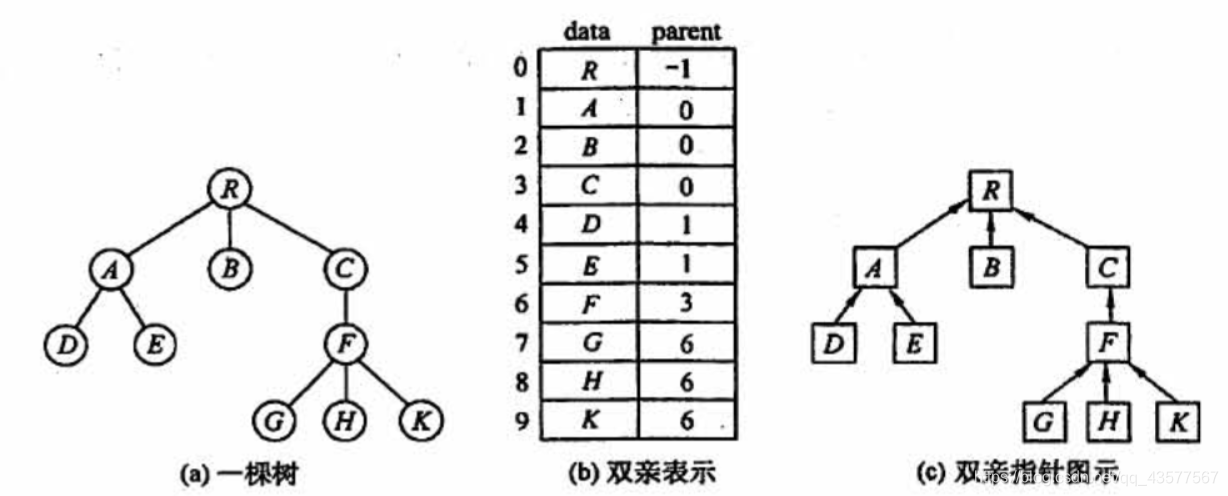
（1）双亲表示法（顺序存储）

• 每个结点中保存指向双亲的伪指针。
  

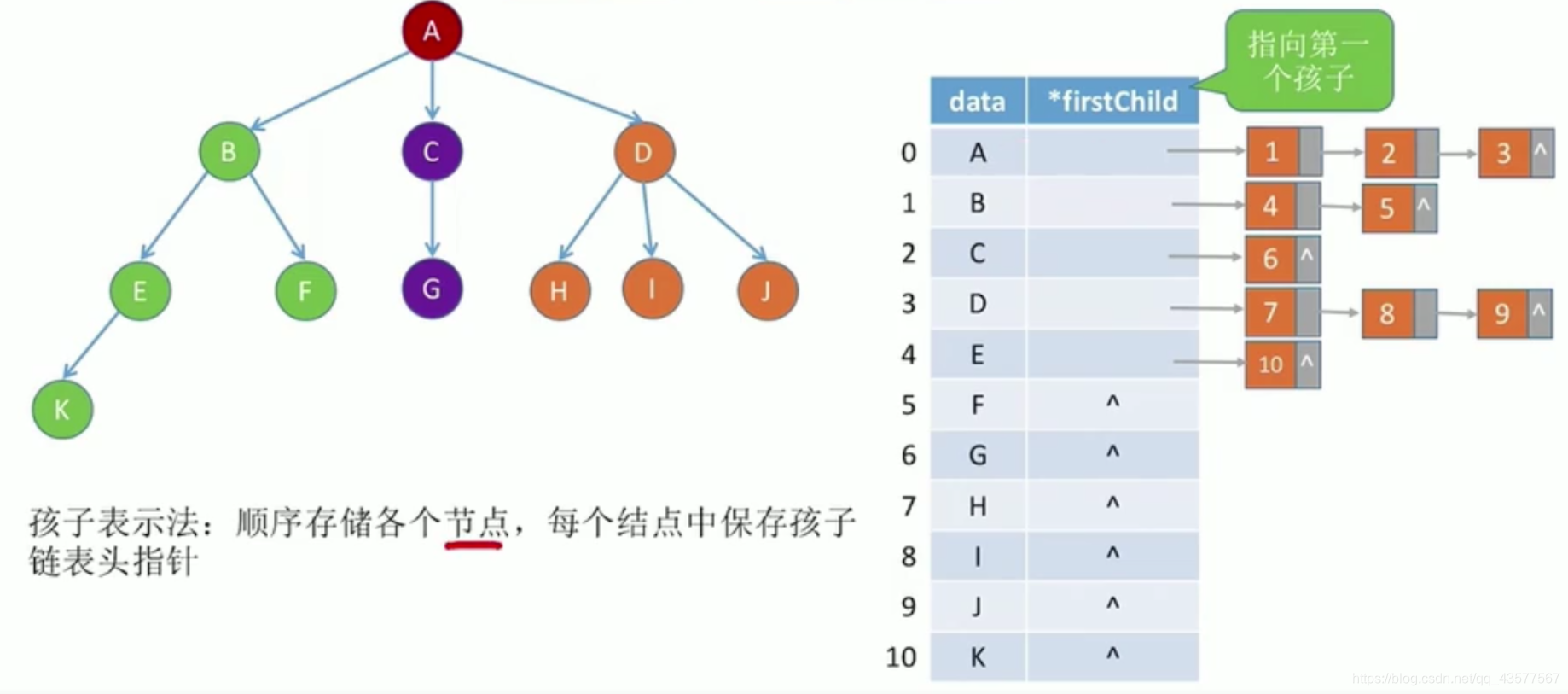
（2）孩子表示法（顺序+链式存储）

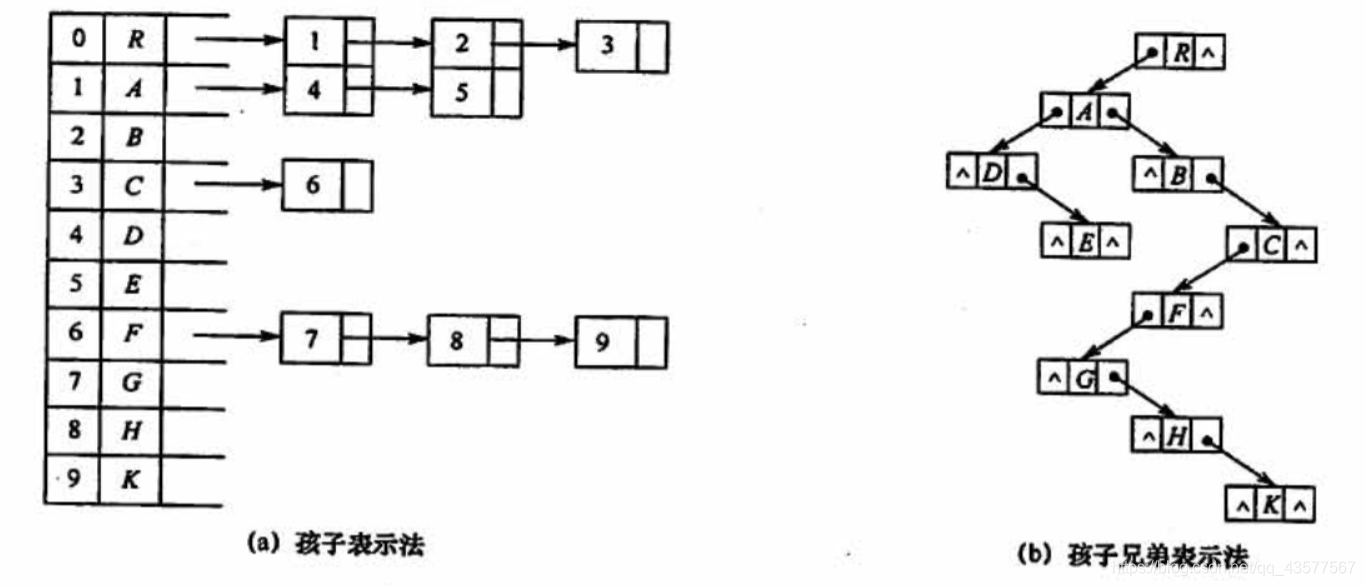
（3）孩子兄弟表示法（链式存储）

2、树、森林与二叉树的转换（简答/填选）（手动推导）

• 联系孩子兄弟表示法思考。“左孩子，右兄弟”。

（1）树转换成二叉树

（2）森林转换成二叉树

（3）二叉树转换成森林

3、树和森林的遍历（了解）

1. 树：先根/后根遍历（深度优先遍历）、层次遍历（广度优先遍历）。
2. 森林：先序遍历、中序遍历
3. 转成二叉树思考。对应关系（选填）
   

三、二叉树的概念（主要考查）

1、二叉树的定义（选填）

1. 特点
   • 每个结点至多只有两棵子树
   • 二叉树是有序树，若将左右子树颠倒，则成为另一棵不同的二叉树。
2. 空二叉树：n=0。
3. 二叉树与度为2的有序树的区别（选填）
   • 度为2的树至少有3个结点；二叉树可以为空。
   • 二叉树无论孩子数是否为2，均需要确定其左右次序。

   引申：度为m的树、m叉树的区别
   

2、特殊二叉树（选填）

（1）满二叉树

1. 定义：一棵高度为h，且含有2^h-1个结点的二叉树。
2. 特点：
   ①只有最后一层有叶子结点；
   ②不存在度为1的结点。
   ③按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1，结点i的父节点为[i/2]。

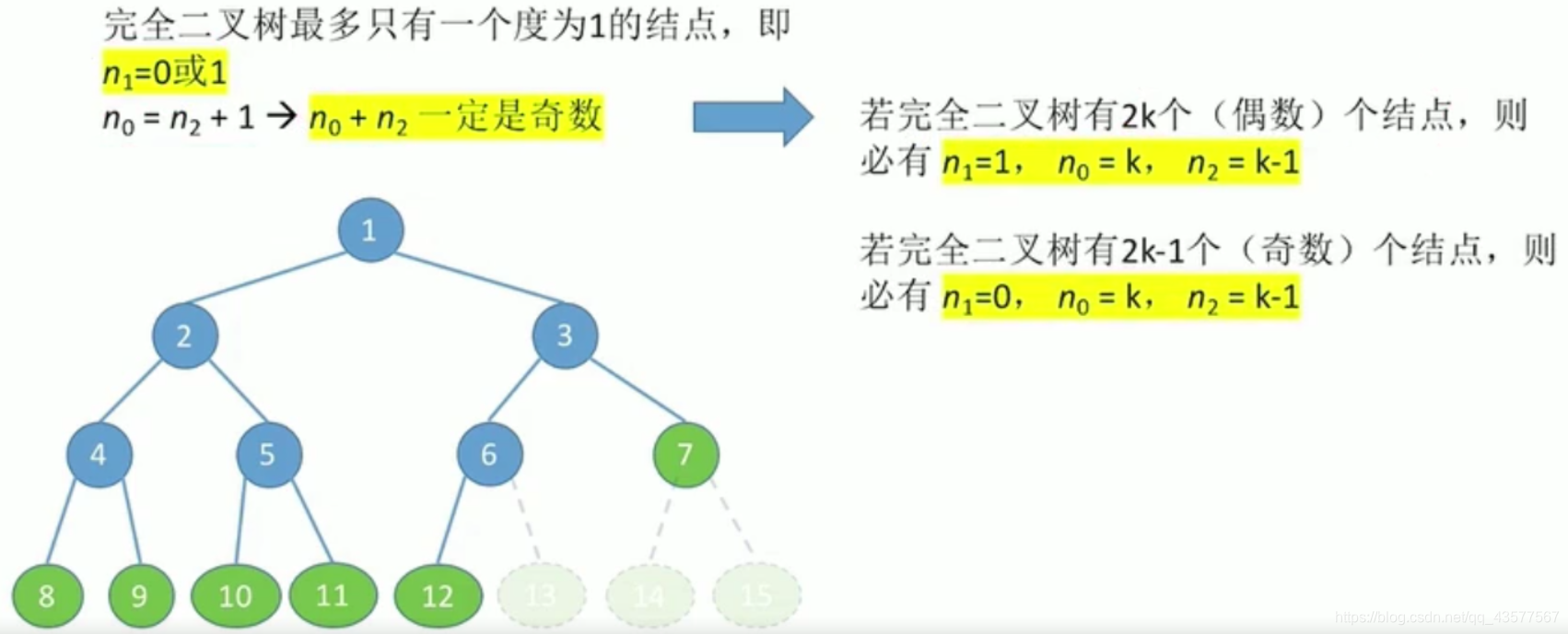
（2）完全二叉树

1. 定义：当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应。
2. 满二叉树是特殊的完全二叉树。
3. 特点：
   ①只有最后两层可能有叶子结点。
   ②最多只有一个度为1的结点（eg.图中6）。
   ③同满二叉树③。
   ④若i≤[n/2]，则结点i为分支结点，否则为叶子结点。
   ⑤若n为奇数，则每个分支结点都有左孩子右孩子；若n为偶数，则编号最大（n/2）的分支结点只有左孩子。

（3）二叉排序树

1. 左子树上所有结点的关键字均小于根结点；右子树均大于。左子树和右子树又各是一棵二叉排序树。
2. 二叉排序树可用于元素的排序、搜索。

（4）平衡二叉树

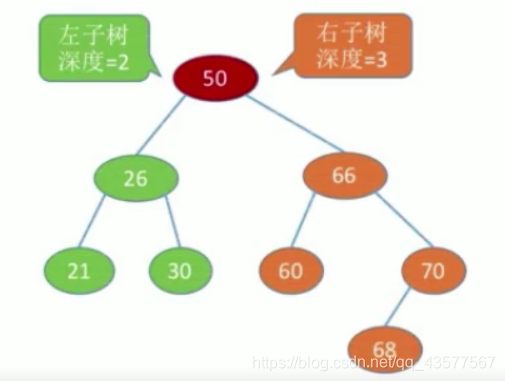
1. 定义：树上任一结点的左子树和右子树的深度之差不超过1。（考多次）
2. 平衡二叉树能有更高的搜索效率。

3、二叉树的6大性质（选填）

1. n0 = n2 + 1。（叶子结点比二分支结点多一个）
2. 二叉树的第i层上最多有2^(i-1)（i≥1）个结点。同m叉树。
3. 高度为k的二叉树最多有2^(h-1)（h≥1）个结点（满二叉树）。代入m叉树性质得出。
4. 有 n 个结点的完全二叉树，各结点从上到下、从左到右依次编号，则有：
   ①如果i>1，则i结点的双亲为[i/2]。i为奇，右孩子；i为偶，左孩子。
   ②如果 2i≤n，i的左孩子为2i；否则无左孩子
   ③如果 2i+1≤n，i的右孩子为 2i+1；否则无右孩子
   ④结点i所在层次（深度）为[log2(i)]+1。
5. 具有 n 个结点的完全二叉树的高度为[log2(n+1)]或[log2(n)]+1。
6. Catalan 函数：给定 n 个结点，能构成 h(n)种不同的二叉数。
   
7. 附：完全二叉树的不同度的结点个数计算
   

四、二叉树的存储结构

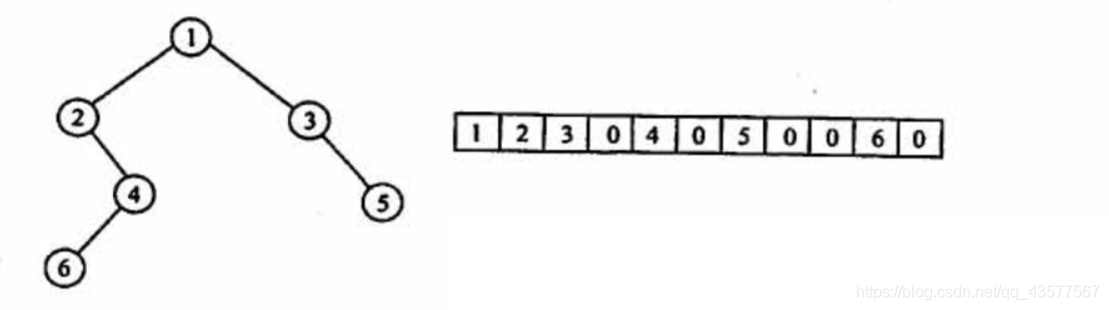
1、顺序存储结构（了解）

• 按照从上至下、从左至右的顺序存储二叉树。
• 要把二叉树的结点编号与完全二叉树对应起来。补全为空（0）。
• 结论：只适合存储完全二叉树。
• 会手动推导：
  

2、链式存储结构（主要实现）

• 结点结构和存储结构
  
  
• 代码描述：

  typedef struct BiTNode{
  	ElemType data;                        //数据域
  	struct BiTNode *lchild, *rchild;      //左右孩子指针
  	//struct BiTNode *parent;             //父节点指针——三叉链表
  }BiTNode, *BiTree;
  

• 创建并插入：

  struct ElemType{
  	int value;
  };
  
  typedef struct BiTNode{
      ElemType data;                        
   	struct BiTNode *lchild, *rchild;      
   }BiTNode, *BiTree;
  
  //定义一棵空树
  BiTree root = NULL;
  
  //插入根结点
  root = (BiTree)malloc(sizeof(BiTNode));
  root->data = {1};
  root->lchild = NULL;
  root->rchild = NULL;
  
  //插入新结点
  BiTNode *p = (BiTNode *)malloc(sizeof(BiTnode));
  p->data = {2};
  p->lchild = NULL;
  p->rchild = NULL;
  root->lchild = p;     //作为根节点的左孩子
  

• n个结点的二叉链表共有n+1个空链域，可以用于构造线索二叉树。（共2n个指针域，n-1个结点上有一个指针域）

五、二叉树的遍历（必有一个大题）

1、递归遍历

• 二叉树的递归特性：
  ①要么是个空二叉树
  ②要么是由根+左子树+右子树组成的二叉树
• 先序遍历：根左右（NLR）→前缀表达式
  中序遍历：左根右（LNR）→中缀表达式（+界限符）
  后序遍历：左右根（LRN）→后缀表达式
• 空间复杂度O(h)

（1）先序遍历

1. 若二叉树为空，则什么也不做；
2. 若二叉树非空：
   1. 访问根结点；
   2. 先序遍历左子树；
   3. 先序遍历右子树。

void PreOrder(BiTree T){
	if(T!=NULL){
		visit(T);              //访问根结点
		PreOrder(T->lchild);   //递归遍历左子树
		PreOrder(T->rchild);   //递归遍历右子树
    }
}

（2）中序遍历

void InOrder(BiTree T){
	if(T!=NULL){
		InOrder(T->lchild);   //递归遍历左子树
		visit(T);              //访问根结点
		InOrder(T->rchild);   //递归遍历右子树
    }
}

（3）后序遍历

void PostOrder(BiTree T){
	if(T!=NULL){
		PostOrder(T->lchild);   //递归遍历左子树
		PostOrder(T->rchild);   //递归遍历右子树
		visit(T);              //访问根结点
    }
}

2、非递归遍历

（1）先序遍历

• 访问结点操作放在入栈操作前

void PreOrder2(BiTree T){
	InitStack(S);                //初始化栈S
	BiTree p=T;                  //p是遍历指针
	while(p || IsEmpty(S)){      //栈不空或p不空时循环
		if(p){                   //一路向左
			visit(p); Push(S,p); //访问当前结点，并入栈
			p = p->lchild;       //左孩子不空，一直向左走
		}
		else{                    //出栈，并转向出栈结点的右子树
			Pop(S,p);            //栈顶元素出栈
			p = p->rchild;       //向右子树走，p赋值为当前结点的右孩子
		}                        //返回while循环继续进入if-else语句
	}
}

（2）中序遍历

1. 沿着根的左孩子，依次入栈，直到左孩子为空。（说明已找到可以输出的结点）
2. 栈顶元素出栈并访问：若其右孩子为空，继续执行2；
3. 若其右孩子不空，将右子树转执行1.

void InOrder2(BiTree T){
	InitStack(S);                
	BiTree p=T;                  
	while(p || IsEmpty(S)){      
		if(p){                  
			Push(S,p);           //当前结点入栈
			p = p->lchild;     
		}
		else{                    //出栈，并转向出栈结点的右子树
			Pop(S,p); visit(p);  //栈顶元素出栈，访问出栈结点
			p = p->rchild;       
		}                        //返回while循环继续进入if-else语句
	}                                                          
}

（3）后序遍历

1. 沿着根的左孩子，依次入栈，直到左孩子为空。
2. 读栈顶元素：若其右孩子不空且未被访问过，将右子树转执行1。(需要分清是从左/右子树返回的)
3. 否则栈顶元素出栈并访问。

void PostOrder(BiTree T){
	InitStack(S);
	p = T;
	r = NULL;
	while(p || IsEmpty(S)){
		if(p){                            //走到最左边
			push(S,p);
			p = p->lchild;
		}
		else{                             //向右
			GetTop(S,p);                  //读栈顶元素
			if(p->rchild && p->rchild!=r) //若右子树存在，且未被访问过
				p = p->rchild;            //转向右
			else{                         //否则，弹出结点并访问
				pop(S,p);                 //将结点弹出
				visit(p->data);           //访问该结点
				r = p;                    //记录最近访问过的结点
				p = NULL;                 //结点访问完后，重置p指针
			}
		}//else
	}//while
}

（4）层次遍历

1. 初始化一个辅助队列
2. 根结点入队
3. 若队列非空，则队头结点出队，访问该结点，并将其左、右孩子插入队尾（如果存在）。
4. 重复3直至队列为空

//链式队列结点
typedef struct LinkNode{
	BiTNode *data;                    //存指针而不是结点
	struct LinkNode *next;
}LinkNode;

typedef struct{
	LinkNode *front, *rear;          //队头队尾
}LinkQueue;

//层次遍历
void LevelOrder(BiTree T){
	LinkQueue Q;
	InitQueue(Q);                    //初始化辅助队列
	BiTree p;
	EnQueue(Q,T);                    //根结点入队
	while(!IsEmpty(Q)){              //队列不空则循环
		DeQueue(Q, p);               //队头结点出队
		visit(p);                    //访问出队结点
		if(p->lchild!=NULL) 
			EnQueue(Q, p->lchild);   //左孩子入队
		if(p->rchild!=NULL)
			EnQueue(Q, p->rchild);   //右孩子入队
	}
}

（5）由遍历序列构造二叉树（选填）

• 可以唯一确定一棵二叉树（必须有中序遍历序列）
  • 前序+中序
    
  • 后序+中序
    
  • 层序+中序
    

六、线索二叉树（考的少，不用实现）

1、概念

• 定义：使该序列中的每个结点（第一个和最后一个除外）都有一个直接前驱和直接后继。why：加快查找结点前驱和后继的速度。
• 结点结构及标志域含义（了解）
  
  
• 存储结构描述（了解）

  Typedef struct ThreadNode{
  	ElemType data;                         //数据元素
  	struct ThreadNode *lchild, *rchild;    //左右孩子指针
  	int ltag, rtag;                        //左右线索标志
  }ThreadNode, *ThreadTree;
  

2、中序线索二叉树的构造（手动推导）

中序遍历序列：B D A E C

3、先序线索二叉树的构造

先序遍历序列：A B D G E C F

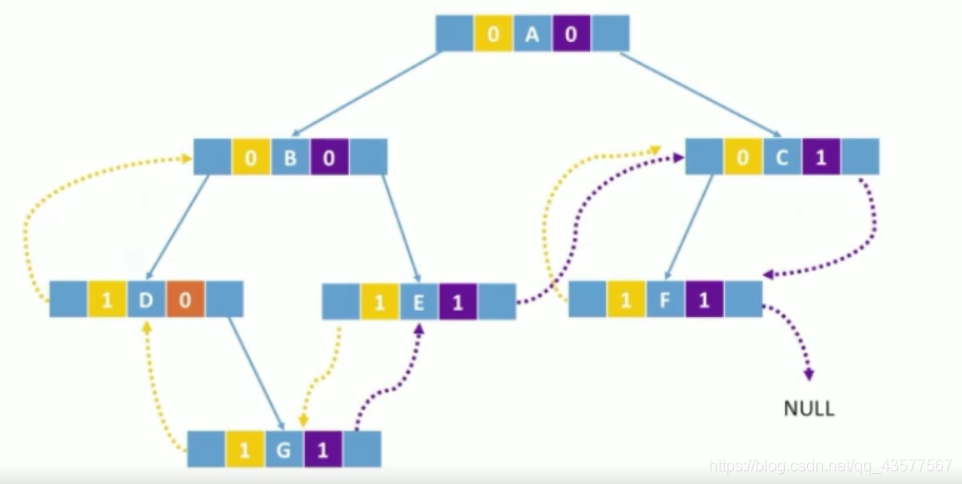
4、后序线索二叉树的构造

后序遍历序列：G D E B F C A

七、树与二叉树的应用（算法+简答）

1、并查集（少）

1. 树表示并查集
   
   其中负数表示当前结点是树的根结点，负数的绝对值表示树中结点的个数/集合中元素的个数。正数表示所属的树的根结点。
2. S1∪S2可能的表示方法：将其中一个子集合根结点的双亲指针指向另一个集合的根结点。
   

2、二叉排序树（BST）（算法实现）

（1）定义（选填）

• 也称二叉查找树。
• 左子树结点值<根结点值<右子树结点值。
• 进行中序遍历，可以得到一个递增的有序序列。

（2）二叉排序树的查找

1. 若树非空，目标值与根结点的值比较；
2. 若相等则查找成功；
3. 若小于根结点，则在左子树上查找，否则在右子树上查找。
4. 查找成功返回结点指针，查找失败返回NULL。

//二叉排序树的结点
typedef struct BSTNode{
	int key;
	struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;

//在二叉排序树中查找值为key的结点(递归实现)
BSTNode *BST_Search(BSTree T, int key){
	while(T!=NULL && key!=T->key){    //若树空或等于根结点，则结束循环
		if(key<T->key)
			T = T->lchild;            //小于则在左子树上查找
		else
			T = T->rchild;            //大于则在右子树上查找
	}
	return T;
}

//递归实现
BTNode *BSTSearch(BTNode T,int key){
	if(T == NULL) 
		return NULL;                 //查找失败
	if(key == T->key) 
		return T;                    //查找成功
	else if(key < BT->key) 
		return BSTSearch(T->lchild,key);
	else 
		return BSTSearch(T->rchild,key);
}

（3）二叉排序树的插入

1. 若原二叉排序树为空，则直接插入结点；
2. 否则若关键字k小于根结点值，则插入到左子树；
3. 若关键字k大于根结点值，则插入到右子树。

//在二叉排序树插入关键字为k的新结点（递归实现）
int BST_Insert(BSTree &T, int k){
	if(T=NULL){             //原树为空，新插入的结点为根结点
		T = (BSTree)malloc(sizeof(BSTNode));
		T->key = k;
		T->lchild = T->rchild = NULL;
		return 1;           //返回1，插入成功
	}
	else if(k == T->key)    //树中存在相同关键字的结点，插入失败
		return 0;
	else if(k < T->key)     ?/插入到T的左子树
		return BST_Insert(T->lchild,k);
	else                    //插入到T的右子树
		return BST_Insert(T->rchild,k);
}

（4）二叉排序树的构造

• 设str=[45, 24, 53, 45, 12, 24]
  

//按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BiTree &T, KeyType str[], int n){
	T = NULL;             //初始时T为空树
	int i=0;
	while(i<n){           //依次将每个关键字插入到二叉排序树中
		BST_Insert(T,str[i]);
		i++;
	}
}

（5）二叉排序树的删除

• 分情况处理
  • 若被删除结点z是叶子结点，则直接删除。
  • 若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。
  • 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删除这个直接后继（或直接前驱），转换成1、2两种情况。
    • z的后继：z的右子树中最左下结点（该结点没有左子树）
    • z的前驱：z的左子树中最右下结点（该节点没有右子树）
• 示例
  

（6）查找效率分析

• 查找长度：在查找运算中，需要比对关键字的次数。反映时间复杂度。
• 查找成功的平均查找长度ASL（选填）
  
  • 如图（a），ASL = (1 + 22 + 34 + 4*3) / 10 = 2.9
    如图（b），ASL = (1+2+3+4+5+6+7+8+9+10)/10=5.5
  • 最好情况：n个结点的二叉树最小高度为[log2(n)+1]，ASL=O(log2(n))。（平衡二叉树）
  • 最坏情况：每个结点只有一个分支，树高h=结点数n。ASL=O(n)。
• 查找失败的平均查找长度：（假设停在每个空节点的概率相同）
  
  ASL = (37 + 42) / 9 = 3.22

3、平衡二叉树（重要）

（1）定义（选填）

• 简称平衡树（AVL树）——树上任一结点的左子树和右子树的高度之差不超过1。
• 结点的平衡因子 = 左子树高 - 右子树高
  • 
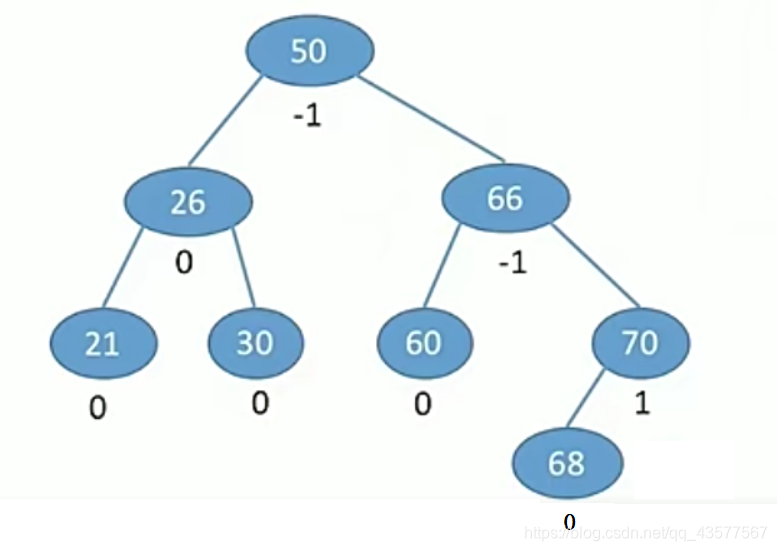
  • 平衡因子的值只可能是-1，0或1。

（2）平衡二叉树的插入（手动推导 简答）

• 调整最小不平衡子树，使其他祖先结点恢复平衡。

• 	最小不平衡子树A
  LL	在A的左孩子的左子树中插入导致不平衡
  RR	在A的右孩子的右子树中插入导致不平衡
  LR	在A的左孩子的右子树中插入导致不平衡
  RL	在A的右孩子的左子树中插入导致不平衡

• 只有左孩子才能右上旋；只有右孩子才能左上旋。

[1] LL平衡旋转（右单旋转）

• 二叉排序树的特性：BL<B<HR<A<AR
• 实现：将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树作为A结点的左子树。

[2] RR平衡旋转（左单旋转）

• 特性：AL<A<BL<B<BR
• 实现：将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，二B的原左子树则成为A结点的右子树。

[3] LR平衡旋转（先左后右双旋转）

• 特性：BL<B<CL<C<CR<A<AR
• 实现：先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置。

[4] RL平衡旋转（先右后左双旋转）

• 特性：AL<A<CL<C<CR<B<BR
• 先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置。

（3）平衡二叉树的查找

• 过程和二叉排序树完全相同
• 查找效率分析：
  • 假设以nh表示深度为h的平衡树中含有的最少结点数，则有n0=0，n1=1，n2=2，有nh = n(h-1) + n(h-2) + 1。
  • 最大深度=平均查找长度=时间复杂度=O(log2(n))

4、哈夫曼树和哈夫曼编码（建树+编码+求WPL）

（1）定义（选填）

1. 结点的权：有某种现实含义的数值。
2. 结点的带权路径长度：从树的根到该结点的路径长度（经过的边数）与该结点上权值的乘积。
3. 树的带权路径长度：树中所有叶节点的带权路径长度之和（WPL）（计算）
   
4. 哈夫曼树：也称最优二叉树。带权路径长度（WPL）最小的二叉树。

（2）哈夫曼树的构造（手动推导 简答）

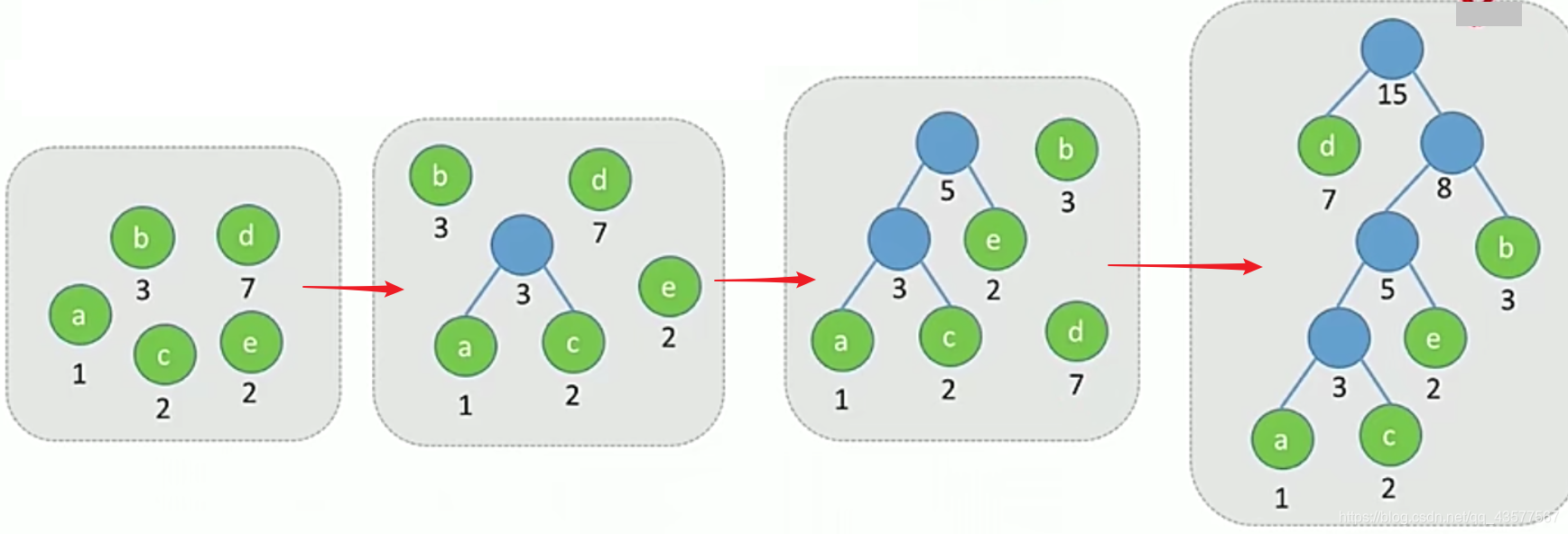
• 算法描述（给定n个权值分别为w1,w2,…,wn的结点）
  • ①将这n个结点分别作为n棵仅含有一个结点的二叉树，构成森林F。
  • ②构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和。
  • ③从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
  • ④重复步骤②和③，直到F中只剩下一棵树为止。
• 例子：WPL(min) = 17 + 23 + 32 + 41 + 4*2 = 31
  
• 哈夫曼树特点
  • 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。
  • 构造过程中共新建了n-1个结点，因此结点总数为2n-1。
  • 哈夫曼树中不存在度为1的结点。
  • 哈夫曼树并不唯一，但WPL必然相同且为最优。

（3）哈夫曼编码

• 固定长度编码：每个字符用相等长度的二进制位表示。
• 可变长度编码：允许对不同字符用不等长的二进制位表示。
• 前缀编码：没有一个编码是另一个编码的前缀。（无歧义）
• 由哈夫曼树得到哈夫曼编码：字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值。可用于数据压缩。
• 示例：WPL = 145 + 3(13 + 12 + 16) + 4*(5 + 9) = 224
  
  • 上述例子中，如果采用3位固定长度编码，二进制编码长度为3*(45+13+12+16+9+5)=300。采用哈夫曼树的WPL可视为最终编码得到二进制编码的长度，因此哈夫曼编码共压缩了25%的数据。