数据库元组关系演算

最新推荐文章于 2024-09-13 14:37:07 发布

这个不知道什么感觉

最新推荐文章于 2024-09-13 14:37:07 发布

阅读量7.4k

点赞数 1

本文链接：https://blog.csdn.net/qq_43668118/article/details/87560084

版权

元组关系演算

之前学习了一下关系代数表达式，现在再学习一下元组关系的演算，这样就全了。这篇东西的符号打出来费了好多时间，比较麻烦，还好看着还能看懂，关键是全文本的，好下面开始正文。

为了讨论方便，先允许关系的基数是无限的。然后再对这种情况下定义的演算作适当的修改，保证关系演算中的每一个公式表示的是有限关系。

在元组关系演算系统中，称 {t|Φ(t)} 为元组演算表达式。其中 t 是元组变量， Φ(t) 为元组关系演算公式，简称公式。
它由原子公式和运算符组成。

原子公式有三类：

(1) R(t)

R 是关系名， t 是元组变量。 R(t) 表示 t 是 R 中的元组。于是，关系 R 可表示为： {t|R(t)}

(2) t[i] θ u[j]

t 和 u 是元组变量， θ 是算术比较运算符。 t[i] θ u[j] 表示断言 “ 元组 t 的第 i 个分量与元组 u 的第 j 个分量满足比较关系 θ ” 。例如， t[2] < u[3] 表示元组 t 的第 2 个分量小于元组 u 的第 3 个分量。

(3) t[i] θ c 或 c θ t[i]
这里 c 是常量，该公式表示 “t 的第 i 个分量与常量 C 满足比较关系 θ” 。例如： t[4]=3 表示元组 t 的第 4 个分量等于 3 。

在关系演算中定义了 “ 自由元组变量 ” 和 “ 约束元组变量 ” 的概念。这些概念和谓词演算中的概念完全一样。若公式中的一个元组变量前有 “ 全称量词 ” 或 “ 存在量词 ” ，则称该变量为约束元组变量，否则称自由元组变量。

公式可以递归定义如下：

    (l) 每个原子公式是公式。
    (2) 如果 Φ 1 和 Φ 2 是公式，则 Φ 1 ∧ Φ 2 、 Φ 1 ∨ Φ 2 、﹁ Φ1 也是公式。分别表示：
        ① 如果 Φ 1 和 Φ 2 同时为真。则 Φ 1 ∧ Φ 2 才为真，否则为假；
        ② 如果 Φ 1 和 Φ 2 中一个或同时为真，则 Φ 1 ∨ Φ 2 为真，仅 Φ 1 和 Φ 2 同时为假时， Φ 1 ∨ Φ 2 才为假；
        ③ 如果 Φ 1 真，则﹁ Φ 1 为假。
    (3) 若 Φ 是公式，则 ∃ t(Φ) 也是公式。其中符号 ∃ 是存在量词符号， ∃ t(Φ) 表示：
        若有一个 t 使 Φ 为真，则 ∃ t(Φ) 为真，否则 ∃ t(Φ) 为假。
    (4) 若 Φ 是公式，则 ∀ t( Φ ) 也是公式。其中符号 ∀ 是全称量词符号， ∀ t( Φ ) 表示：
        如果对所有 t ，都使 Φ 为真，则 ∀ t( Φ ) 必为真，否则 ∀ t( Φ ) 为假。
    (5) 在元组演算公式中，各种运算符的优先次序为：
        ① 算术比较运算符最高；
        ② 量词次之，且 ∃ 的优先级高于 ∀ 的优先级；
        ③ 逻辑运算符最低，且﹁的优先级高于 ∧ 的优先级， ∧ 的优先级高于 ∨ 的优先级；
        ④ 加括号时，括号中运算符优先，同一括号内的运算符之优先级遵循 ①②③ 各项。
    (6) 有限次地使用上述五条规则得到的公式是元组关系演算公式，其他公式不是元组关系演算公式。

一个元组演算表达式 {t|Φ(t)} 表示了使 Φ(t) 为真的元组集合。
关系代数的运算均可以用关系演算表达式来表示 ( 反之亦然 ) 。下面用关系演算表达式来表示五种基本运算：

(1) 并

R ∪ S={t|R(t) ∨ S(t)}

(2) 差

R － S={t|R(t) ∧ ﹁ S(t)}

(3) 笛卡尔积

R×S={t (n+m) |( ∃ u (n) )( ∃ v (m) )(R(u) ∧ S(v) ∧ t[1]=u[1] ∧ ... ∧ t[n]=u[n] ∧ t[n+1]=v[1] ∧ ... ∧ t[n+m]=v[m])}

注： t (n+m) 表示 t 有目数 (n+m)

(4) 投影

π t1,t2,...,tk (R)={t (k) |( ∃ u )(R(u) ∧ t[1]=u[i1] ∧ ...t[k]=u[ik] )}

(5) 选择

σ F (R)={t|R(t) ∧ F}

注： F 是公式。 F 用 t[i] 代替运算对象 i 得到的等价公式。

     例 1 查询信息系 (IS 系 ) 全体学生：
        S IS ={Student(t) ∧ t[5]='IS'}
     例 2 查询年龄小于 20 岁的学生。
        S 20 ={Student(t) ∧ t[4]<20}

例 3 查询学生的姓名和所在系。
S={t (2) |( ∃ u)(Student(u) ∧ t[1]=u[2] ∧ t[2]=u[5])}

上面定义的关系演算允许出现无限关系。例如 {t| ﹁ R(t)} 表示所有不属于 R 的元组 ( 元组的目数等于 R 的目数 ) 。要求出这些可能的元组是做不到的，所以必须排除这类无意义的表达式。把不产生无限关系的表达式称为安全表达式，所采取的措施称为安全限制。安全限制通常是定义一个有限的符号集 dom(Φ) ， dom(Φ) 一定包括出现在 Φ 以及中间结果和最后结果的关系中的所有符号 ( 实际上是各列中值的汇集 ) 。 dom(Φ) 不必是最小集。

     当满足下列条件时，元组演算表达式 {t|Φ(t)} 是安全的：
    （ 1 ）如果 t 使 Φ(t) 为真，则 t 的每个分量是 dom(Φ) 中的元素。
    （ 2 ）对于 Φ 中每一个形如 ( ∃ t)(W(u)) 的子表达式，若 u 使 W(u) 为真，则 u 的每个分量是 dom(Φ) 中的元素。
    （ 3 ）对于 Φ 中每一个形如 ( ∀ t)(W(u)) 的子表达式，若 u 使 W(u) 为假，则 u 的每个分量必属于 dom(Φ) 。换言之，若 u 某一分量不属于 dom(Φ) ，则 W(u) 为真。

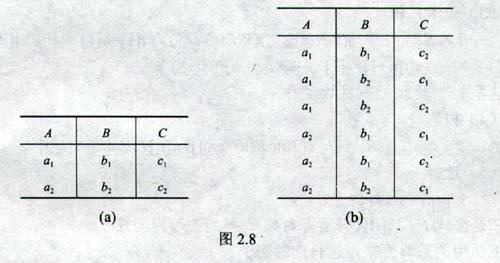
例 4 设有关系 R 如图 2.8(a) ， S={t| ﹁ R(t)} ，若不进行安全限制，则可能是一个无限关系。所以定义

dom(Φ)= π A (R) ∪ π B (R) ∪ π C (R)

={{a1,a2},{b1,b2},{c1,c2}}

则 S 是 dom(Φ) 中各域值中元素的笛卡儿积与 R 的差集。结果如图 2.8(b) 。注意，在做笛卡儿积时各个域中的元素不能搞混。

元组.jpg