王道数据结构编程题（二叉树）

呦，又写BUG呢

已于 2022-03-25 22:13:36 修改

阅读量2.2k

点赞数

分类专栏：数据结构与算法文章标签：架构数据结构数据库

于 2022-03-07 17:20:55 首次发布

本文链接：https://blog.csdn.net/qq_43686863/article/details/123334790

版权

数据结构与算法专栏收录该内容

92 篇文章 5 订阅

订阅专栏

文章目录

1.非递归后序遍历二叉树。
2.二叉树自下而上、自右至左层次遍历。
3.非递归求二叉树的高度。
4.根据先序和中序遍历序列创建二叉树，并输出其后序遍历序列。
5.判断二叉树是否是完全二叉树。
6.计算一颗二叉树所有双分支结点个数
7.交换所有结点的左右子树，并输出交换后的先序序列。
8.求先序遍历序列中第k个结点的值。
9.对于树中每个元素值为x的结点，删去以它为根的子树，并释放相应空间，先序遍历新的二叉树。
10.打印值为x的结点的所有祖先。
11.求两个结点的最近公共祖先。
12.求非空二叉树的宽度（即结点数最多的一层的结点数）。
13.已知一颗满二叉树的先序序列，求其后序序列。
14.将二叉树的叶子结点从左到右链接为一个单链表，遍历此单链表。
15.二叉树相似指的是两棵二叉树都是空的二叉树或者都只有一个根节点再或者二者左、右子树也分别相似，判断两棵二叉树是否相似。
16.在中序线索二叉树里查找指定结点在后序中的前驱。
17.求二叉树带权路径长度。
18.将给定的表达式树转换为等价的中缀表达式。
附：测试用例示意图
附：tree.h与tree.c
附：stack.h与stack.c
附：queue.h与queue.c

1.非递归后序遍历二叉树。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
DEBHIFGCA
DBFCA

#include <stdio.h>
#include "tree.h"
#include "stack.h"

void BiTreePostOrderTraverse(BiTree root) {
    SqStack S;
    BiTNode *now_node, *last_pop_node;

    StackInit(&S);
    StackPush(&S, root);
    last_pop_node = NULL;
    while (!StackEmpty(S)) {
        StackGetTop(S, &now_node);
        if (last_pop_node == NULL) {
            /*previous action is push*/
            if (now_node->right) StackPush(&S, now_node->right);
            if (now_node->left) StackPush(&S, now_node->left);
            if (!now_node->left && !now_node->right) {
                /*now_node is a leaf node*/
                StackPop(&S, &now_node);
                printf("%c", now_node->data);
                last_pop_node = now_node;
            }
        } else {
            /*previous action is pop*/
            if (last_pop_node == now_node->left || last_pop_node == now_node->right) {
                /*last_pop_node is now_node's child*/
                StackPop(&S, &now_node);
                printf("%c", now_node->data);
                last_pop_node = now_node;
            } else {
                /*last_pop_node is now_node's left brother*/
                last_pop_node = NULL;
            }
        }
    }
    printf("\n");
}

void BiTreePostOrderTraverse_(BiTree root) {
    SqStack S;
    BiTNode *now_node, *last_pop_node;

    StackInit(&S);
    now_node = root;
    last_pop_node = NULL;
    while (now_node || !StackEmpty(S)) {
        if (now_node) {
            StackPush(&S, now_node);
            now_node = now_node->left;//access left subtree
        } else {
            StackGetTop(S, &now_node);
            if (now_node->right && now_node->right != last_pop_node) {
                now_node = now_node->right;//access right subtree
            } else {
                /*no right child or last_pop_node is right child*/
                StackPop(&S, &now_node);
                printf("%c", now_node->data);
                last_pop_node = now_node;
                now_node = NULL;
            }
        }
    }
    printf("\n");
}

int main() {
    char str[MaxSize] = "";
    BiTree T;
    int i;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;

        BiTreeCreate(&T, str, &i);
        BiTreePostOrderTraverse(T);
        /*BiTreePostOrderTraverse_(T);*/
        BiTreeDestroy(&T);
    }
    return 0;
}

2.二叉树自下而上、自右至左层次遍历。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
IHGFEDCBA
FDCBA

#include <stdio.h>
#include "tree.h"
#include "stack.h"
#include "queue.h"

void BiTreeInvertLevelTraverse(BiTree T) {
    SqStack S;
    SqQueue Q;
    BiTree now_node = NULL;

    StackInit(&S);
    QueueInit(&Q);
    EnQueue(&Q, T);
    while (!QueueEmpty(Q)) {
        DeQueue(&Q, &now_node);
        StackPush(&S, now_node);
        if (now_node->left) EnQueue(&Q, now_node->left);
        if (now_node->right) EnQueue(&Q, now_node->right);
    }
    while (!StackEmpty(S)) {
        StackPop(&S, &now_node);
        printf("%c", now_node->data);
    }
    printf("\n");
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;

        BiTreeCreate(&T, str, &i);
        BiTreeInvertLevelTraverse(T);
        BiTreeDestroy(&T);
    }
    return 0;
}

3.非递归求二叉树的高度。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
4
3

#include <stdio.h>
#include "tree.h"
#include "queue.h"

int GetHeight(BiTree T) {
    SqQueue Q;
    BiTree now_node;
    int this_line = 1, next_line = 0;
    int height = 0;

    if (!T) return 0;//an empty tree
    QueueInit(&Q);
    EnQueue(&Q, T);
    while (!QueueEmpty(Q)) {
        DeQueue(&Q, &now_node);
        this_line--;
        if (now_node->left) {
            EnQueue(&Q, now_node->left);
            next_line++;
        }
        if (now_node->right) {
            EnQueue(&Q, now_node->right);
            next_line++;
        }
        if (this_line == 0) {
            this_line = next_line;
            next_line = 0;
            height++;
        }
    }
    return height;
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        printf("%d\n", GetHeight(T));
        BiTreeDestroy(&T);
    }
    return 0;
}

4.根据先序和中序遍历序列创建二叉树，并输出其后序遍历序列。

输入样例：
9
ABDECFHIG
DBEAHFICG
5
ABDCF
DBACF
0

输出样例：
DEBHIFGCA
DBFCA

#include <stdio.h>
#include "tree.h"

/**
 * 根据先序序列与中序序列构建二叉树
 * @param pre_order 整棵树的先序序列
 * @param in_order 整棵树的中序序列
 * @param pre_begin 当前二叉树对应先序序列起始位置
 * @param pre_end 当前二叉树对应先序序列结束位置
 * @param in_begin 当前二叉树对应中序序列起始位置
 * @param in_end 当前二叉树对应中序序列结束位置
 * @return 当前二叉树（构建完成）的根结点
 */
BiTree PreInCreat(char *pre_order, char *in_order, int pre_begin, int pre_end, int in_begin, int in_end) {
    int in_now_pos = in_begin;//当前结点在中序序列中的位置
    int left_amount, right_amount;//左右子树的结点个数

    BiTNode *node = (BiTNode *) malloc(sizeof(BiTNode));
    node->data = pre_order[pre_begin];//根结点始终是当前先序遍历序列的第一个

    while (in_order[in_now_pos] != node->data) in_now_pos++;//在中序遍历序列中定位当前结点
    left_amount = in_now_pos - in_begin;
    right_amount = in_end - in_now_pos;

    if (left_amount) {
        /*递归建立左子树*/
        node->left = PreInCreat(pre_order, in_order,
                                pre_begin + 1, pre_begin + left_amount,
                                in_begin, in_now_pos - 1);
    } else {
        node->left = NULL;
    }

    if (right_amount) {
        /*递归建立右子树*/
        node->right = PreInCreat(pre_order, in_order,
                                 pre_begin + left_amount + 1, pre_end,
                                 in_now_pos + 1, in_end);
    } else {
        node->right = NULL;
    }
    return node;
}

void PostOrderTraverse(BiTree root) {
    if (root) {
        PostOrderTraverse(root->left);
        PostOrderTraverse(root->right);
        printf("%c", root->data);
    }
}

int main() {
    char pre_str[MaxSize] = "";
    char in_str[MaxSize] = "";
    BiTree T = NULL;
    int n = 0;

    while (scanf("%d", &n) && n != 0) {
        getchar();
        for (int i = 0; i < n; i++) scanf("%c", pre_str + i);
        getchar();
        for (int i = 0; i < n; i++) scanf("%c", in_str + i);
        T = PreInCreat(pre_str, in_str, 0, n - 1, 0, n - 1);
        PostOrderTraverse(T);
        printf("\n");
        BiTreeDestroy(&T);
    }
    return 0;
}

5.判断二叉树是否是完全二叉树。

输入样例：
ABD##E##CFH##I##G##
ABD##E##CF###
#

输出样例：
NO
YES

#include <stdio.h>
#include <stdbool.h>
#include "tree.h"
#include "queue.h"

/**
 * 通过层序遍历判断一个空结点后面是否还有非空结点
 * @param T 
 * @return 
 */
bool IsComplete(BiTree T) {
    SqQueue Q;
    BiTNode *node = NULL;

    if (!T) return false;
    QueueInit(&Q);
    EnQueue(&Q, T);
    while (!QueueEmpty(Q)) {
        DeQueue(&Q, &node);
        if (node) {
            /*空结点也入队*/
            EnQueue(&Q, node->left);
            EnQueue(&Q, node->right);
        } else {
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &node);
                if (node) return false;
            }
        }
    }
    return true;
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        printf("%s\n", (IsComplete(T)) ? "YES" : "NO");
        BiTreeDestroy(&T);
    }
    return 0;
}

6.计算一颗二叉树所有双分支结点个数

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
4
1

#include <stdio.h>
#include "tree.h"

int Count(BiTree T) {
    return T ? (Count(T->left) + Count(T->right) + ((T->left && T->right) ? 1 : 0)) : 0;
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        printf("%d\n", Count(T));
        BiTreeDestroy(&T);
    }
    return 0;
}

7.交换所有结点的左右子树，并输出交换后的先序序列。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
ACGFIHBED
ACFBD

#include <stdio.h>
#include "tree.h"

void Swap(BiTree T) {
    if (T) {
        Swap(T->left);
        Swap(T->right);
        BiTNode *tmp = T->left;
        T->left = T->right;
        T->right = tmp;
    }
}

void PreOrderTraverse(BiTree T) {
    if (T) {
        printf("%c", T->data);
        PreOrderTraverse(T->left);
        PreOrderTraverse(T->right);
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        Swap(T);
        PreOrderTraverse(T);
        printf("\n");
        BiTreeDestroy(&T);
    }
    return 0;
}

8.求先序遍历序列中第k个结点的值。

输入样例：
ABD##E##CFH##I##G##
3
ABD###C#F##
5
#

输出样例：
D
F

#include <stdio.h>
#include "tree.h"

void PreOrderTraverse(BiTree T, int k, int *i) {
    if (T) {
        if (*i == k) printf("%c\n", T->data);
        (*i)++;
        PreOrderTraverse(T->left, k, i);
        PreOrderTraverse(T->right, k, i);
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        int k;
        i = 0;
        BiTreeCreate(&T, str, &i);
        scanf("%d", &k);
        getchar();
        i = 1;
        PreOrderTraverse(T, k, &i);
        BiTreeDestroy(&T);
    }
    return 0;
}

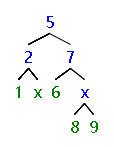
9.对于树中每个元素值为x的结点，删去以它为根的子树，并释放相应空间，先序遍历新的二叉树。

输入样例：
521##x##76##x8##9##
x
#

输出样例：
52176

#include <stdio.h>
#include "tree.h"

void Delete(BiTree *T, char x) {
    if (*T) {
        if ((*T)->data == x) {
            BiTreeDestroy(T);
        } else {
            Delete(&((*T)->left), x);
            Delete(&((*T)->right), x);
        }
    }
}

void PreOrderTraverse(BiTree T) {
    if (T) {
        printf("%c", T->data);
        PreOrderTraverse(T->left);
        PreOrderTraverse(T->right);
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        char x;
        i = 0;
        BiTreeCreate(&T, str, &i);
        scanf("%c\n", &x);
        Delete(&T, x);
        PreOrderTraverse(T);
        printf("\n");
        BiTreeDestroy(&T);
    }
    return 0;
}

10.打印值为x的结点的所有祖先。

输入样例：
ABD##E##CFH##I##G##
H
ABD###C#F##
D
#

输出样例：
FCA
BA

#include <stdio.h>
#include "tree.h"
#include "stack.h"

void GetParents(BiTree T, char x) {
    SqStack S;
    BiTNode *now_node = T, *last_pop = NULL;

    StackInit(&S);
    while (now_node || !StackEmpty(S)) {
        if (now_node) {
            StackPush(&S, now_node);
            now_node = now_node->left;
        } else {
            StackGetTop(S, &now_node);
            if (now_node->right && now_node->right != last_pop) {
                now_node = now_node->right;
            } else {
                StackPop(&S, &now_node);
                /*当前后序栈中的所有元素均为目标结点的祖先*/
                if (now_node->data == x) {
                    while (!StackEmpty(S)) {
                        StackPop(&S, &now_node);
                        printf("%c", now_node->data);
                    }
                }
                
                last_pop = now_node;
                now_node = NULL;
            }
        }
    }
    printf("\n");
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        char x;

        i = 0;
        BiTreeCreate(&T, str, &i);
        scanf("%c\n", &x);
        GetParents(T, x);
        BiTreeDestroy(&T);
    }
    return 0;
}

11.求两个结点的最近公共祖先。

输入样例：
ABD##E##CFH##I##G##
B E
ABD##E##CFH##I##G##
C E
#

输出样例：
B
A

#include <stdio.h>
#include "tree.h"

BiTNode *GetComParent(BiTree T, char p, char q) {
    if (!T) return NULL;
    if (T->data == p || T->data == q) return T;

    BiTNode *left = GetComParent(T->left, p, q);
    BiTNode *right = GetComParent(T->right, p, q);
    if (left && right) {
        return T;
    } else if (left) {
        return left;
    } else if (right) {
        return right;
    } else {
        return NULL;
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        char p, q;

        i = 0;
        BiTreeCreate(&T, str, &i);
        scanf("%c %c\n", &p, &q);
        printf("%c\n", GetComParent(T, p, q)->data);
        BiTreeDestroy(&T);
    }
    return 0;
}

12.求非空二叉树的宽度（即结点数最多的一层的结点数）。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
4
2

#include <stdio.h>
#include "tree.h"

void PreOrderTraverse(BiTree T, int depth, int *count) {
    if (T) {
        count[depth]++;
        PreOrderTraverse(T->left, depth + 1, count);
        PreOrderTraverse(T->right, depth + 1, count);
    }
}

int GetWidth(BiTree T) {
    int count[MaxSize] = {0};
    int max = INT_MIN;

    PreOrderTraverse(T, 0, count);
    for (int i = 0; i < MaxSize; i++) max = (max > count[i]) ? max : count[i];
    printf("%d\n", max);
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        GetWidth(T);
        BiTreeDestroy(&T);
    }
    return 0;
}

13.已知一颗满二叉树的先序序列，求其后序序列。

输入样例：
3
ABC
7
ABDECFG
#

输出样例：
BCA
DEBFGCA

在这里插入图片描述

#include <stdio.h>
#include <math.h>
#include "tree.h"
#include "stack.h"

/**
 * 通过先序序列构造此满二叉树
 * @param T
 * @param str
 * @param n
 */
void GetPost(BiTree *T, char *str, int n) {
    int height = 0, i = 0;
    BiTNode *node = NULL;
    SqStack S;

    while (pow(2, height + 1) - 1 != n) height++;
    StackInit(&S);
    *T = (BiTree) malloc(sizeof(BiTNode));
    StackPush(&S, *T);
    while (!StackEmpty(S)) {
        StackPop(&S, &node);
        node->data = str[i++];
        if (height != 1) {
            /*right child*/
            node->right = (BiTree) malloc(sizeof(BiTNode));
            StackPush(&S, node->right);
            /*left child*/
            node->left = (BiTree) malloc(sizeof(BiTNode));
            StackPush(&S, node->left);
            height--;//next node in stack is current node's left child
        } else {
            /*right child*/
            node->right = (BiTree) malloc(sizeof(BiTNode));
            node->right->data = str[i++];
            node->right->left = node->right->right = NULL;
            /*left child*/
            node->left = (BiTree) malloc(sizeof(BiTNode));
            node->left->data = str[i++];
            node->left->left = node->left->right = NULL;
            //next node in stack is current node's right brother
        }
    }
}

void PostOrderTraverse(BiTree T) {
    if (T) {
        PostOrderTraverse(T->left);
        PostOrderTraverse(T->right);
        printf("%c", T->data);
    }
}

/**
 * 直接处理字符串
 * @param pre 先序序列
 * @param post 后序序列
 * @param pre_begin 当前子树先序起始位置
 * @param pre_end 当前子树先序结束位置
 * @param post_begin 当前子树后序起始位置
 * @param post_end 当前子树后序结束位置
 */
void GetPost_(char *pre, char *post, int pre_begin, int pre_end, int post_begin, int post_end) {
    if (pre_begin <= pre_end) {
        post[post_end] = pre[pre_begin];
        GetPost_(pre, post,
                 pre_begin + 1, (pre_begin + pre_end) / 2,
                 post_begin, (post_begin + post_end)/ 2 - 1);
        GetPost_(pre, post,
                 (pre_begin + pre_end) / 2 + 1, pre_end,
                 (post_begin + post_end)/ 2, post_end - 1);
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int n = 0;

    while (scanf("%d", &n) && n != 0) {
        char post[MaxSize] = "";

        getchar();
        for (int i = 0; i < n; i++) scanf("%c", str + i);
        /*GetPost(&T, str, n);
        PostOrderTraverse(T);
        BiTreeDestroy(&T);*/
        GetPost_(str, post, 0, n - 1, 0, n - 1);
        printf("%s\n", post);
    }
    return 0;
}

14.将二叉树的叶子结点从左到右链接为一个单链表，遍历此单链表。

输入样例：
ABD##E##CFH##I##G##
ABD###C#F##
#

输出样例：
DEHIG
DF

#include <stdio.h>
#include "tree.h"
#include "stack.h"

void Link(BiTree T, BiTNode **head) {
    SqStack S;
    BiTNode *node, *tail = *head;

    StackInit(&S);
    StackPush(&S, T);
    while (!StackEmpty(S)) {
        int is_leaf = 1;

        StackPop(&S, &node);
        if (node->right) {
            StackPush(&S, node->right);
            is_leaf = 0;
        }
        if (node->left) {
            StackPush(&S, node->left);
            is_leaf = 0;
        }
        if (is_leaf) {
            tail->right = node;
            tail = node;
        }
    }
}

void DeLink(BiTNode  **head) {
    BiTNode *cursor = (*head)->right, *tmp;
    while (cursor) {
        tmp = cursor->right;
        cursor->right = NULL;
        cursor = tmp;
    }
    free(*head);
    *head = NULL;
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        BiTNode *head = (BiTNode *) malloc(sizeof(BiTNode));

        i = 0;
        BiTreeCreate(&T, str, &i);
        Link(T, &head);
        for (BiTNode *cursor = head->right; cursor; cursor = cursor->right) printf("%c", cursor->data);
        printf("\n");
        DeLink(&head);//恢复原二叉树并将新建头结点空间释放
        BiTreeDestroy(&T);
    }
    return 0;
}

15.二叉树相似指的是两棵二叉树都是空的二叉树或者都只有一个根节点再或者二者左、右子树也分别相似，判断两棵二叉树是否相似。

输入样例：
ABD##E##CFH##I##G##
ABC##D##EFH##H##I##
ABD##E##CFH##I##G##
ABD##E##CFH##I###
#
#

输出样例：
YES
NO

#include <stdio.h>
#include <stdbool.h>
#include "tree.h"

bool IsSimilar(BiTree T_A, BiTree T_B) {
    if (T_A) {
        if (!T_B) {
            return false;
        } else {
            if (IsSimilar(T_A->left, T_B->left) && IsSimilar(T_A->right, T_B->right)) {
                return true;
            } else {
                return false;
            }
        }
    } else {
        if (T_B) {
            return false;
        } else {
            return true;
        }
    }
}

bool IsSimilar_(BiTree T_A, BiTree T_B) {
    /*without if-else*/
    return (T_A) ? ((!T_B) ? false : ((IsSimilar(T_A->left, T_B->left) && IsSimilar(T_A->right, T_B->right)) ? true : false)) : (T_B) ? false : true);
}

int main() {
    char str_a[MaxSize] = "";
    char str_b[MaxSize] = "";
    BiTree T_A = NULL, T_B = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str_a) && scanf("%[^\n]%*c", str_b)) {
        if (str_a[0] == '#' && str_b[0] == '#') break;
        i = 0;
        BiTreeCreate(&T_A, str_a, &i);
        i = 0;
        BiTreeCreate(&T_B, str_b, &i);
        printf("%s\n", IsSimilar_(T_A, T_B) ? "YES" : "NO");
        BiTreeDestroy(&T_A);
        BiTreeDestroy(&T_B);
    }
    return 0;
}

16.在中序线索二叉树里查找指定结点在后序中的前驱。

输入样例：
421##3##865##7##9##
6
#

输出样例：
7

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 100

typedef struct ThreadNode {
    char data;
    int ltag, rtag;
    struct ThreadNode *lchild, *rchild;
} ThreadNode, *ThreadTree;

void ThreadTreeInit(ThreadTree *root, char *node_data, int *cursor);//通过先序序列初始化二叉树（即构建二叉树但不进行线索化）
void InThread(ThreadTree root, ThreadNode **pre_node);//二叉树中序线索化（子函数）
void InThreadCreate(ThreadTree root);//二叉树中序线索化（主函数）
ThreadNode *GetFirstNode(ThreadTree cursor);//获取中序线索序列的头结点
ThreadNode *GeTNextNode(ThreadTree cursor);//获取中序线索序列的下一个结点
void ThreadTreeDestroy(ThreadTree *root);//释放二叉树内存空间

void ThreadTreeInOrderTraverse(ThreadTree head);//通过中序线索进行中序遍历
void DeInThread(ThreadTree head);//将线索二叉树恢复为普通二叉树

/**
 * 通过中序线索获取后序前驱
 * @param T
 * @param c
 * @return
 */
ThreadNode *GetPostPre(ThreadTree T, char c) {
    ThreadNode *cursor = GetFirstNode(T);
    while (cursor->data != c) {
        cursor = GeTNextNode(cursor);
    }

    if (cursor->rtag == 0) {//非叶结点 有右孩子
        return cursor->rchild;
    } else if (cursor->ltag == 0) {//非叶结点 没有右孩子 有左孩子
        return cursor->lchild;
    } else {//叶子结点
        while (cursor->ltag == 1 && cursor->lchild != NULL) {//顺着左线索寻找祖先
            cursor = cursor->lchild;
        }
        if (cursor->ltag == 0) {//此祖先有左孩子
            return cursor->lchild;
        } else {//此祖先为中序序列首个结点 没有左孩子
            return NULL;
        }
    }
}

int main() {
    char str[MaxSize] = "";
    ThreadTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        ThreadNode *target;
        char c;

        i = 0;

        ThreadTreeInit(&T, str, &i);
        InThreadCreate(T);
        scanf("%c%*c", &c);
        target = GetPostPre(T, c);
        printf("%c\n", target ? target->data : '#');
        ThreadTreeDestroy(&T);
    }
    return 0;
}

/**
 * 通过先序序列初始化二叉树（即构建二叉树但不进行线索化）
 * @param root
 * @param node_data
 * @param cursor
 */
void ThreadTreeInit(ThreadTree *root, char *node_data, int *cursor) {
    if (node_data[*cursor] == '#') {
        *root = NULL;
    } else {
        *root = (ThreadNode *) malloc(sizeof(ThreadNode));
        (*root)->data = node_data[*cursor];
        (*root)->ltag = (*root)->rtag = 0;
        (*cursor)++;
        ThreadTreeInit(&((*root)->lchild), node_data, cursor);
        (*cursor)++;
        ThreadTreeInit(&((*root)->rchild), node_data, cursor);
    }
}

/**
 * 二叉树中序线索化（子函数）
 * @param root
 * @param pre_node
 */
void InThread(ThreadTree root, ThreadNode **pre_node) {
    if (root) {
        InThread(root->lchild, pre_node);//处理左子树
        /*链接前驱线索*/
        if (!root->lchild) {
            root->lchild = *pre_node;
            root->ltag = 1;//1表示线索指针
        }
        /*链接后继线索*/
        if (*pre_node && !(*pre_node)->rchild) {
            (*pre_node)->rchild = root;
            (*pre_node)->rtag = 1;
        }
        *pre_node = root;//将当前结点标记为上一个结点
        InThread(root->rchild, pre_node);//处理右子树
    }
}

/**
 * 二叉树中序线索化（主函数）
 * @param root
 */
void InThreadCreate(ThreadTree root) {
    ThreadNode *last_node = NULL;//存储每个上一次访问的结点
    InThread(root, &last_node);
    last_node->rtag = 1;
}

/**
 * 获取中序线索序列的头结点
 * @param cursor
 * @return
 */
ThreadNode *GetFirstNode(ThreadTree cursor) {
    while (cursor->ltag == 0) {
        cursor = cursor->lchild;
    }
    return cursor;
}

/**
 * 获取中序线索序列的下一个结点
 * @param cursor
 * @return
 */
ThreadNode *GeTNextNode(ThreadTree cursor) {
    return (cursor->rtag) ? cursor->rchild : GetFirstNode(cursor->rchild);
}

/**
 * 通过中序线索进行中序遍历
 * @param head
 */
void ThreadTreeInOrderTraverse(ThreadTree head) {
    for (ThreadNode *cursor = GetFirstNode(head); cursor; cursor = GeTNextNode(cursor)) {
        printf("%c", cursor->data);
    }
}

/**
 * 将线索二叉树恢复为普通二叉树
 * @param head
 */
void DeInThread(ThreadTree head) {
    ThreadNode *cursor = GetFirstNode(head), *tmp;

    while (cursor) {
        tmp = GeTNextNode(cursor);
        if (cursor->ltag == 1) {
            cursor->ltag = 0;
            cursor->lchild = NULL;
        }
        if (cursor->rtag == 1) {
            cursor->rtag = 0;
            cursor->rchild = NULL;
        }
        cursor = tmp;
    }
}

/**
 * 释放二叉树内存空间
 * @param root
 */
void ThreadTreeDestroy(ThreadTree *root) {
    ThreadNode *cursor = GetFirstNode(*root), *tmp;

    while (cursor) {
        tmp = GeTNextNode(cursor);
        free(cursor);
        cursor = tmp;
    }
    *root = NULL;
}

17.求二叉树带权路径长度。

输入样例：
421##3##865##7##9##
321###4#5##
#

输出样例：
62
12

在这里插入图片描述

#include <stdio.h>
#include "tree.h"

void CalculateWPL(BiTree T, int depth, int *WPL) {
    if (T) {
        if (!T->left && !T->right) {
            *WPL += depth * (T->data - 48);
        }
        CalculateWPL(T->left, depth + 1, WPL);
        CalculateWPL(T->right, depth + 1, WPL);
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        int WPL = 0;

        i = 0;
        BiTreeCreate(&T, str, &i);
        CalculateWPL(T, 0, &WPL);
        printf("%d\n", WPL);
        BiTreeDestroy(&T);
    }
    return 0;
}

18.将给定的表达式树转换为等价的中缀表达式。

输入样例：
*+a##b##*c##-#d##
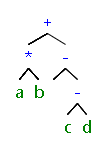
+*a##b##-#-c##d##
#

输出样例：
(a+b)*(c*(-d))
(a*b)+(-(c-d))

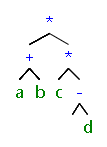
#include <stdio.h>
#include "tree.h"

void GetInFixExpression(BiTree T, int height) {
    if (T) {
        if (T->left || T->right) {
            if (height != 0) printf("(");
            GetInFixExpression(T->left, height + 1);
        }
        printf("%c", T->data);
        if (T->right) {
            GetInFixExpression(T->right, height + 1);
            if (height != 0) printf(")");
        }
    }
}

int main() {
    char str[MaxSize] = "";
    BiTree T = NULL;
    int i = 0;

    while (scanf("%[^\n]%*c", str) && str[0] != '#') {
        i = 0;
        BiTreeCreate(&T, str, &i);
        GetInFixExpression(T, 0);
        printf("\n");
        BiTreeDestroy(&T);
    }
    return 0;
}

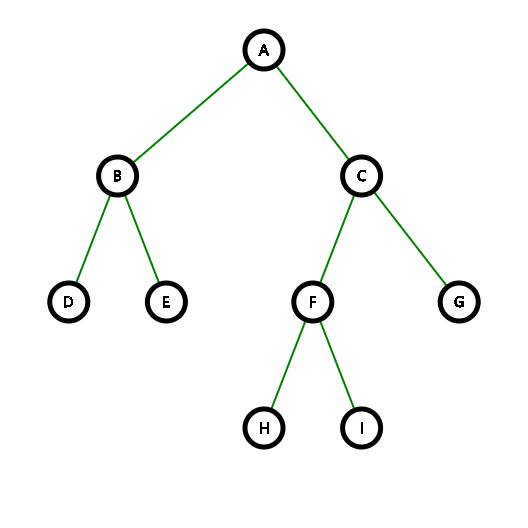
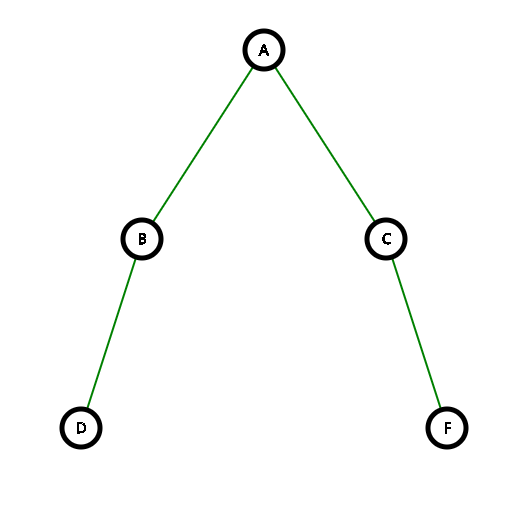
附：测试用例示意图

附：tree.h与tree.c

tree.h

#ifndef CODE_TREE_H
#define CODE_TREE_H

#include <stdlib.h>

#define MaxSize 100

typedef struct BiTNode {
    int data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTreeCreate(BiTree *root, char *node_data, int *cursor);

void BiTreeDestroy(BiTree *root);

#endif

tree.c

#include "tree.h"

void BiTreeCreate(BiTree *root, char *node_data, int *cursor) {
    if (node_data[*cursor] == '#') {
        *root = NULL;
    } else {
        *root = (BiTree) malloc(sizeof(BiTNode));

        (*root)->data = node_data[*cursor];
        (*cursor)++;
        BiTreeCreate(&((*root)->left), node_data, cursor);
        (*cursor)++;
        BiTreeCreate(&((*root)->right), node_data, cursor);
    }
}

void BiTreeDestroy(BiTree *root) {
    while (*root) {
        BiTreeDestroy(&(*root)->left);
        BiTreeDestroy(&(*root)->right);
        free(*root);
        *root = NULL;
    }
}

附：stack.h与stack.c

stack.h

#ifndef CODE_STACK_H
#define CODE_STACK_H

#include <stdbool.h>
#include "tree.h"

#define ElemType BiTree

typedef struct SqStack {
    ElemType data[MaxSize];
    int top;
} SqStack;

void StackInit(SqStack *stack);
bool StackEmpty(SqStack stack);
bool StackPush(SqStack *stack, ElemType e);
bool StackPop(SqStack *stack, ElemType *e);
bool StackGetTop(SqStack stack, ElemType *e);

#endif

stack.c

#include "stack.h"

void StackInit(SqStack *stack) {
    stack->top = -1;
}

bool StackEmpty(SqStack stack) {
    return (stack.top == -1) ? true : false;
}

bool StackPush(SqStack *stack, ElemType e) {
    if (stack->top == MaxSize - 1) return false;

    stack->data[++stack->top] = e;
}

bool StackPop(SqStack *stack, ElemType *e) {
    if (StackEmpty(*stack)) return false;

    *e = stack->data[stack->top--];
    return true;
}

bool StackGetTop(SqStack stack, ElemType *e) {
    if (StackEmpty(stack)) return false;

    *e = stack.data[stack.top];
    return true;
}

附：queue.h与queue.c

queue.h

#ifndef CODE_QUEUE_H
#define CODE_QUEUE_H

#include <stdlib.h>
#include <stdbool.h>
#include "tree.h"

#define ElemType BiTree

typedef struct SqQueue {
    ElemType data[MaxSize];
    int front, rear;
} SqQueue;

void QueueInit(SqQueue *Q);

bool QueueEmpty(SqQueue Q);

bool EnQueue(SqQueue *Q, ElemType e);

bool DeQueue(SqQueue *Q, ElemType *e);

#endif

queue.c

#include "queue.h"

void QueueInit(SqQueue *Q) {
    Q->front = Q->rear = 0;
}

bool QueueEmpty(SqQueue Q) {
    return (Q.front == Q.rear) ? true : false;
}

bool EnQueue(SqQueue *Q, ElemType e) {
    if ((Q->rear + 1) % MaxSize == Q->front) return false;

    Q->data[Q->rear] = e;
    Q->rear = (Q->rear + 1) % MaxSize;
    return true;
}

bool DeQueue(SqQueue *Q, ElemType *e) {
    if (QueueEmpty(*Q)) return false;

    *e = Q->data[Q->front];
    Q->front = (Q->front + 1) % MaxSize;
    return true;
}