傅里叶级数的理解与简单推导

本文重点在于理解傅里叶级数的思想，对于公式的推导仅作泛泛而谈，在正式推导公式之前我想先简单的谈一谈对函数进行傅里叶级数展开有何意义，也即为什么我们要将一个函数进行傅氏变换？
分解与合成是一种朴素的思想，有的时候可以将一个复杂的问题分解成若干个小问题逐个击破，当每一个小的问题解决以后，大的问题也就随之解决。傅里叶变换也是基于这个思想的，它可以将一个函数f(x)分解成若干正弦、余弦函数的和，从而使得原有的一些运算变得更加简洁。傅氏变换是一门数学分支的基础，它就是调和分析，我国著名数学家华罗庚先生认为，把已知函数展开成傅里叶级数的运算就叫做调和分析，调和分析也正是从傅里叶级数和傅里叶变换开始发展壮大起来的。我们知道，一般函数可以展开成泰勒级数的形式，我们不禁要问道，除了泰勒级数这种展开的方式以外，还有没有其他的级数展开方式？答案是肯定的。1807年，法国数学家Baron Jean Baptiste Joseph Fourier在求解热传导方程的时候，发现解函数可以由三角函数构成级数形式表示从而提出函数可以展开成三角级数的无穷级数，这一发现极大地推动了偏微分方程编值问题的研究，Fourier于1822年出版了专著《热的解析理论》，这部著作将Euler、Bernoulli等人运用三角级数的方法发展成内容丰富的一般理论。不得不说的是，傅里叶变换是求解微分方程数值 解的有力工具，这是由三角函数的微积分不变性所决定的，即若对正余弦函数求导，仅仅改变其幅值和相位，而不改变其原有的函数形状。下面我们就来看一下如何将函数进行傅里叶展开。
我们可以先做一些简单尝试，将问题简化。考虑有如下函数f(x) ，在[a,b] 上连续，如果要用不同的余弦函数对其进行累加，设有如下形式：
其中，$a_i(i=0,1,2,......,n)$为各个余弦函数前的系数，这些系数都是未知的。$k_i(i=0,1,2,......,n)$是各余弦函数的角频率，这里我们假设$k_i>0$ 并且不存在相同的两个或者多个角频率。为了简化分析，我们假设余弦函数的初始相位都为0。一旦选定一组{$k_i$} ,也就意味着各余弦函数确定下来，我们的目的就变成了求未知系数{$a_i$} ,我们可以在区间[a,b] 上任取m(m=n+1)个互不相同的数，并且记他们的值分别$x_1,x_2,x_3,...,x_m$。将这些值分别代入式(1)中我们就得到了如下的方程组：

这相当于有n+1 个方程来求解n+1 未知数。方程组可以写成如下矩阵形式：
设
则有$AX=B(4)$
解可得 $X=A^{-1}B(5)$
这样我们便求得了各个余弦函数前的系数{$a_i$}.由于我们之前的角频率{$k_i$}是任意选取的，所以选取不同的{$k_i$} 也将会解得不同的系数{$a_i$} 通过这种方法，我们将函数f(x) 写成了余弦函数累加的形式，问题似乎已经得到了解决。但是我们做进一步的考虑，上述方法需要求解矩阵的逆，当余弦函数的个数n增加时，求逆运算的复杂性也会随之增加，这好像违背了我们初衷——计算反而变得更加复杂了。这样的话将函数展开成余弦函数累加的形式就显得意义不大了。聪明的小伙伴们也许会问道，既然角频率{$k_i$} 是任意选取的，那么，我们可不可以通过选取特定的角频率来简化我们对系数{$a_i$} 的求解？至少说我们能否不涉及到矩阵的求逆运算？为了回答这个问题，我们先来看看余弦函数的一些基本的性质。
我们知道，初相位为0的余弦函数可以写成如下形式：
它具有如下的一些性质：
第一，具有微积分不变性，即对其进行求导或者积分仅改变幅值和相位大小而不改变形状，这也是我们想要运用三角函数来表达其他函数的初衷。
第二，余弦函数具有周期性，且其最小正周期为

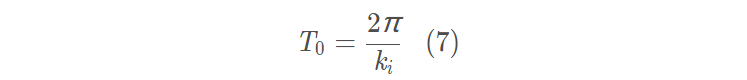
实际上，它拥有无数个周期,即
$T=n{T}_0(n=\pm 1,\pm 2,\pm 3,\pm 4,.......)$ (8)
第三，余弦函数在一个周期内做定积分结果为0，即$${\int }_{\frac{-T}{2}}^{\frac{T}{2}}{a}_{i}cox(k_{i}x)dx=0(9)$$ 由这个性质可以做一下简单的推广。设有两个余弦函数，它们有着相同的周期T，则它俩乘积的积分为：
这里我们用到了积化和差公式，它是一个三角恒等关系。等式右边的第一项积分为0，对于第二项积分，当$k_i\ne k_j$时，它的值为0，当$k_i=k_j$时，它的值为$\frac{1}{2}{a}_i{a}_{j}T$。
所以上述积分值为
在了解了以上的性质以后，我们继续回到函数f(x)的展开。现在有一个很自然的想法，那就是能不能利用在整个周期内定积分为0的性质来简化我们的过程？为了便于分析，我们可以继续对展开的条件进行约束。
我们假设被展开函数定义在区间$[-\pi ,\pi ]$上，并且我们按照一定的规则来选取角频率，它们是这样被规定的：
$k_i=i(i=0,1,2,3,.......)(12)$
即{$k_i$}是初值为0，公差为1的等差数列。除了$k_0$ 以外，其余各项对应的最小周期为：
$$\frac{2}{1}\pi ,\frac{2}{2}\pi ,\frac{2}{3}\pi ,\frac{2}{4}\pi ......$$
事实上，它们拥有一个共同的周期，即$2\pi$。
式(1)中$k_0$ 所对应的项事实上是一个常数，它的值为：
$$a_{0}cos(0x)=a_0(13)$$
稍加思考我们便可以知道，如果我们用这样的一组余弦函数来叠加表示函数f(x)的话，那么函数f(x)也将是周期函数，并且它的周期也将是$2\pi$。有了上面这些铺垫以后，我们再来求各项系数就变得比较简单了。很容易想到，如果在等式(1)两端乘以$cos(k_{0}x)$并且对每一项在$[-\pi ,\pi ]$上进行积分，那么我们有如下的等式成立：
$${\int }_{-\pi }^{\pi }f(x)cos(k_{i}x)dx=\pi a_i(14)$$
其中，等式的右边的结果是基于这样一个事实：

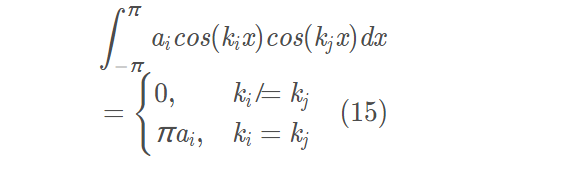
这个可以由等式(10)和(11)当T取值为$2\pi$时得到。这样我们就可以通过求定积分的方法来求得各项系数，在这个过程中并没有涉及到复杂的矩阵求逆运算。我们现在将其梳理一下。
设f(x)为定义在$[-\pi ,\pi ]$上的函数，假设其可以展开成如等式(1)所示的各项余弦函数的求和形式，如果说余弦函数的个数为无穷个的话，那么我们有如下的式子成立:
$$f(x)=\sum _{i=0}^{\infty }{a}_{i}cos(k_{i}x)(16)$$
我们可以通过式(14)来求解各余弦函数的系数，即：
$$a_i=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)cos(k_{i}x)dx(17)$$其中， { k i } \{k_i\} {ki​}是这样的等差数列：
$$k_i=i(i=0,1,2,3,.......)$$这样我们就求得了f(x)通过余弦函数展开的形式，我们称式(17)为f(x)的余弦级数展开。
或许有小伙伴会问，既然f(x)可以用余弦函数展开，那么我们可以用正弦函数来展开么？回答当然是肯定的。这里，我们不加证明地直接给出f(x)的正弦函数展开：$$f(x)=\sum _{i=0}^{\infty }{b}_{i}sin(k_{i}x)dx(18)$$ $$b_i=\frac{1}{\pi }{\int }_{\pi }^{\pi }f(x)sin(k_{i}x)dx(19)$$
同样地, { k i } \{k_i\} {ki​}是这样的等差数列：$$k_i=i(i=0,1,2,3,......)$$
我们称式(19)为f(x)的正弦级数展开。事实上，它的证明和余弦函数展开如出一辙。
下面我们来讨论这样一个问题，是不是所有的定义在$[-\pi ,\pi ]$上的函数f(x)都可以用上述两种展开方法展开呢？（这里我们仅考虑f(x)是连续的）答案显然是否定的，聪明的小伙伴们很快就能发现上面的推导其实是存在问题的。我们回过头来看等式的右边，可以发现它其实是一个偶函数，即
$$\sum _{i=0}^{\infty }{a}_{i}cos(-k_{i}x)=\sum _{i=0}^{\infty }{a}_{i}cos(k_{i}x)(20)$$这也就是说，如果用余弦级数来表示函数f(x)的话，我们将得到f(x)必定为偶函数，也就是说，如果f(x)不为偶函数，我们将无法通过余弦函数展开。
同样的道理，如果用正弦级数来表示函数f(x)的话，我们将得到f(x)必定为奇函数，也就是说，如果f(x)不为奇函数，我们将无法通过正弦函数展开。
那么我们仅仅只能对奇函数或者偶函数进行展开么？这样的话就太局限了！
然而,聪明的你肯定想到了解决这个问题的办法，那就是将两者相结合起来。我们有如下展开：$$f(x)=\sum _{i=0}^{\infty }[a_{i}cos(k_{i}x)+b_{i}sin(k_{i}x)(21)$$其中，各项系数的求取仍然由式(17)和式(19)给出。在这里，我们只需补充一个简单的事实，即:$${\int }_{-\pi }^{\pi }cos(k_{i}x)sin(k_{j}x)dx=0(22)$$其中, { k i } \{k_i\} {ki​}是这样的等差数列：
$$k_i=i(0,1,2,3,.....)$$
我们称式(21)为f(x)在$[-\pi ,\pi ]$上的傅里叶级数展开。
上述f(x)的周期均为$2\pi$，我们很容易将其推广到任意周期T的情况。我们假设三角函数的角频率按照如下规则选取：$$k_i=\frac{2\pi }{T}i(i=0,1,2,3,.....)(23)$$其傅里叶级数展开的形式并没有改变，需要改变的仅仅是系数的求取，即：$$a_i=\frac{2\pi }{T}{\int }_{\frac{-T}{2}}^{\frac{T}{2}}f(x)cos(k_{i}x)dx$$ $$b_i=\frac{2}{T}{\int }_{\frac{-T}{2}}^{\frac{T}{2}}f(x)sin(k_i)dx(24)$$式(24)是周期为T的三角级数展开。
到这里傅里叶级数的推导就告一段落了，它表明我们可以将一个存在于特定区间上的周期函数f(x)展开成三角级数的形式。我们还可以作进一步的思考，这样的展开对周期内不连续的情况是否成立？是否存在一种变换可以对非周期的函数进行展开？

我是$OK欣$，如果有不足之处或者存有疑问，欢迎小伙伴们一起讨论交流。