说明:
- 题目来自PTA平台的C语言与数据结构考研模拟卷(1)
- 部分题目没答案是因为博主也做错了,不知道正确答案
- 如果有不会做的题目或者知道正确答案,可以评论或者私信我,谢谢
选择题
2-1
若有以下说明和定义
typedef int *INTEGER;
INTEGER a,*b;
那么以下叙述正确的是:
| 选项 | |
|---|---|
| A | a 是 int 型的指针变量 |
| B | b 是 int 型的一级指针变量 |
| C | a 是 int 型变量 |
| D | 程序中可用 INTEGER 代替 int 类型名 |
解析:a 是 int 型的指针变量,b 是 int 型的二级指针变量。
2-2
下列程序段的输出结果是:
int k=2, s=0;
switch(k) {
case 2: s++; k++;
case 1: s++;
case 3: s+=1;
switch(s){
case 2: s+=2; break;
default: k++; break;
}
default: s+=3;
}
printf("%d#%d#", s, k);
| 选项 | |
|---|---|
| A | 1#3# |
| B | 6#4# |
| C | 3#2# |
| D | 3#4# |
2-3
执行语句:for(i=1;i++<4;);后变量 i 的值是:
| 选项 | |
|---|---|
| A | 3 |
| B | 4 |
| C | 5 |
| D | 不定 |
2-4
若 k、s的当前值分别为 4、0,执行语句 while(k--)s+=k; 后 k、s值分别为:
| 选项 | |
|---|---|
| A | 0、10 |
| B | -1、10 |
| C | 0、6 |
| D | -1、6 |
解析:当第四轮循环开始时,k为0,循环结束,k-1=-1,s=3+2+1+0=6。
2-5
编译运行下列程序的输出结果是:
void fun(int a, int b, int c)
{ c =a*b;
}
int main( )
{ int c;
fun(4,3,c);
printf("%d",c);
return 0;
}
| 选项 | |
|---|---|
| A | 0 |
| B | 12 |
| C | 编译错误 |
| D | 无法确定 |
解析:由于函数并未改变c的值,所以c为初始值,然而c为局部变量且没有赋初值,故无法确定。
2-6
输入 ABCDEFG时,下列程序的输出结果是:
int f(char s[])
{ if(*s == '\0') return 0;
else return 1+f(s+1);
}
int main()
{ char s[10];
gets(s);
printf("%d",f(s)/2 );
return 0;
}
| 选项 | |
|---|---|
| A | 0 |
| B | 3 |
| C | 4 |
| D | 7 |
2-7
下列程序的输出结果是:
# include <stdio.h>
int x=1;
int f(int x)
{ static int k=0;
return (k++) + x;
}
int main()
{ int k;
for(k=1; k<4; k++)
printf("%d#", f(k+x));
}
| 选项 | |
|---|---|
| A | 3#4#5# |
| B | 2#3#4# |
| C | 2#4#6# |
| D | 3#5#7# |
解析:k为静态变量,重新赋值不改变当前的值;f函数中先返回k+x的值,然后执行k++。
2-8
如果有宏定义 #define MUL(x,y) (x*y);那么表达式 MUL(MUL(2+3,6),4+2)-7的值是:
| 选项 | |
|---|---|
| A | 173 |
| B | 75 |
| C | 113 |
| D | 69 |
解析:注意替换的时候不要忘记外层的括号。
2-9
已知 ‘9’ 的 ASCII 码是 57,‘a’ 的 ASCII 码是 97,‘A’ 的 ASCII 码是 65。
以下程序结果是:
int main()
{ char a[40]="a\065\0b";
puts(a);
return 0;
}
| 选项 | |
|---|---|
| A | aA |
| B | a\065\0b |
| C | a5 |
| D | a |
解析:输出为a5,a\065\0b中\065为5的ASCII码的八进制,后面的\0为结束符号。
2-10(暂时未知正确答案,只知道C是错的)
设有如下函数,期望返回一个字符串:
char *p(int n)
{ ______________________________
return s+n;
}
该函数内的下划线处填入以下哪个选项时,将不能正确得到函数返回的字符串?
| 选项 | |
|---|---|
| A | char *s=“abcdefghij”; |
| B | char s[]=“abcdefghij”; |
| C | static char s[]=“abcdefghij”; |
| D | char *s; s=(char *)malloc(10); strcpy(s,“abc123”); |
解析:。
2-11
若有以下程序段:
struct dent {
int no;
int *m;
};
int a = 1, b = 2, c = 3;
struct dent s[3] = {{101, &a}, {102, &b}, {103, &c}};
int main()
{ struct dent *p = s;
……
}
则以下表达式中值为 2 的是:
| 选项 | |
|---|---|
| A | ((p+1))->m |
| B | *(p++)->m |
| C | (*p).m+1 |
| D | *(++p)->m |
解析:A选项为2的地址,B选项为1,C选项为1的地址+1,D选项为正确选项。
2-12(暂时未知正确答案,只知道A是错的)
如果有变量定义 char **pp[10];,那么下面说法正确的是:
| 选项 | |
|---|---|
| A | pp 是指向字符指针的指针变量 |
| B | pp 是字符指针 |
| C | pp[4] 是字符指针 |
| D | pp 是数组名 |
解析:。
2-13
设有以下语句,则变量 c的十进制数是:
char a = 3, b = 6, c;
c = a^b<<4-2;
| 选项 | |
|---|---|
| A | 27 |
| B | 20 |
| C | 78 |
| D | 97 |
解析:优先级:减号 > 左移号 > 异或,2^(3<<2)=27。
2-14
运行下列程序,得到文件的内容是:
void fun(char *fname, char *st)
{ FILE *myfile; int i;
myfile = fopen(fname,"w" );
for(i=0; i<strlen; i++)
fputc(st[i], myfile);
fclose(myfile);
}
int main()
{ fun("f_", "Programming_");
fun("f_", "in_C_is_fun");
return 0;
}
| 选项 | |
|---|---|
| A | Programming_in_C_is_fun |
| B | in_C_is_fun |
| C | f_in_C_is_fun |
| D | in_C_is_fun_ |
解析:w 打开只写文件,若文件存在则文件长度清为0,故文件中只有第二个字符串。
2-15
运行该程序的输出结果是:
#include <stdio.h>
int main()
{ int x=5, y=3, z=1;
printf("%d %d\n",(++x,y++),z+1);
return 0;
}
| 选项 | |
|---|---|
| A | 6 4 |
| B | 6 3 |
| C | 4 2 |
| D | 3 2 |
解析:逗号表达式取后面的一项y++,故最后输出的是3。
2-16(暂时未知正确答案,只知道C是错的)
以下给出四种算法的时间复杂度,如果当 N=100 时它们对应的运行时间依次是:A 算法 100 毫秒、B 算法 30 毫秒、C 算法 20 毫秒、D 算法 10 毫秒,则当 N=200 时,哪种算法最快?
| 选项 | |
|---|---|
| A | O ( N ) O(N) O(N) |
| B | O ( N 2 ) O(N^2) O(N2) |
| C | O ( N 3 ) O(N^3) O(N3) |
| D | O ( N 4 ) O(N^4) O(N4) |
2-17(暂时未知正确答案,只知道D是错的)
对于顺序存储和链式存储的长度为 N 的线性表,访问结点的时间复杂度分别为:
| 选项 | |
|---|---|
| A | O ( 1 ) 和 O ( 1 ) O(1)和O(1) O(1)和O(1) |
| B | O ( 1 ) 和 O ( N ) O(1)和O(N) O(1)和O(N) |
| C | O ( N ) 和 O ( 1 ) O(N)和O(1) O(N)和O(1) |
| D | O ( N ) 和 O ( N ) O(N)和O(N) O(N)和O(N) |
2-18
有五个元素以 2、4、5、1、3 的顺序进栈 S,每个出栈元素都必须立刻进入队列 Q,问哪个不是合法的出队列 Q 的序列?
| 选项 | |
|---|---|
| A | 2 4 5 1 3 |
| B | 3 1 5 4 2 |
| C | 1 3 5 2 4 |
| D | 1 5 3 4 2 |
2-19
18 叉树中只有 5 个度为 3 的结点、2 个度为 18 的结点和若干叶结点,则叶结点个数是:
| 选项 | |
|---|---|
| A | 45 |
| B | 51 |
| C | 52 |
| D | 无法确定 |
2-20
某非空二叉树的先序遍历和中序遍历序列相同,则该树的形态是:
| 选项 | |
|---|---|
| A | 只有一个根结点 |
| B | 没有度为 1 的结点 |
| C | 所有结点只有左孩子 |
| D | 所有结点只有右孩子 |
2-21
我们记 L 为对左子树的递归访问,R 为对右子树的递归访问,T 为对根结点的访问。则对二叉搜索树进行什么遍历可以得到从大到小的有序序列?
| 选项 | |
|---|---|
| A | RTL |
| B | LTR |
| C | RLT |
| D | TLR |
2-22
将 26, 13, 44, 51, 98, 37, 58, 66 顺序插入一棵初始为空的 AVL 树。下列句子中哪句是错的?
| 选项 | |
|---|---|
| A | 44 是根结点 |
| B | 51 和 98 是兄弟 |
| C | 26 是 37 的父结点 |
| D | 37 和 66 是兄弟 |
2-23
设最大堆的层序遍历结果为 { 95, 72, 86, 50, 65, 12, 23, 42 }。用线性时间复杂度的算法将该堆调整为最小堆。则该树的中序遍历结果为:
| 选项 | |
|---|---|
| A | 95, 65, 42, 72, 12, 86, 23, 50 |
| B | 12, 42, 23, 65, 72, 86, 50, 95 |
| C | 12, 42, 23, 50, 65, 86, 95, 72 |
| D | 72, 50, 42, 65, 12, 86, 23, 95 |
2-24
由分别带权为 7、2、3、5 的四个叶子结点构成一棵哈夫曼树,该树的带权路径长度为?
| 选项 | |
|---|---|
| A | 17 |
| B | 22 |
| C | 32 |
| D | 34 |
2-25
对于有向图,其邻接表表示比邻接矩阵表示更易于:
| 选项 | |
|---|---|
| A | 求一个顶点的出边邻接点 |
| B | 求一个顶点的入度 |
| C | 进行图的深度优先遍历 |
| D | 进行图的广度优先遍历 |
2-26(暂时未知正确答案,只知道B是错的)
对于一个具有 N 个顶点的无向图,要连通所有顶点至少需要多少条边?
| 选项 | |
|---|---|
| A | N-1 |
| B | N |
| C | N+1 |
| D | N/2 |
2-27
对于给定的有向图如右图,其强连通分量为:

| 选项 | |
|---|---|
| A | {1,2} {3,4,5} |
| B | {1} {2,4,5} {3} |
| C | {1,2,4} {3} {5} |
| D | {1,3,4} {2,5} |
2-28
设一棵非空完全二叉树 T 的所有叶节点均位于同一层,且每个非叶结点都有 2 个子结点。若 T 有 1024 个叶结点,则 T 的结点总数是:
| 选项 | |
|---|---|
| A | 2047 |
| B | 2048 |
| C | 2049 |
| D | 1048576 |
2-29
已知二叉搜索树如右图所示,则元素之间不应满足的大小关系是:
| 选项 | |
|---|---|
| A | B<C<A |
| B | B<D<C |
| C | D<B<A |
| D | D<C<A |
2-30
在一个有权无向图中,如果顶点 b 到顶点 a 的最短路径长度是 13,顶点 c 与顶点 a 之间存在一条长度为 3 的边。那么下列说法中哪句是正确的?
| 选项 | |
|---|---|
| A | c 到 b 的最短路径长度就是 16 |
| B | c 到 a 的最短路径长度就是 3 |
| C | c 到 b 的最短路径长度不小于 10 |
| D | c 到 b 的最短路径长度与 b 到 a 的最短路径长度无关 |
2-31
设无向图为 G=(V,E),其中 V={v1,v2,v3,v4},E={(v1,v2),(v3,v4),(v4,v1),(v2,v3),(v2,v4)}。则每个顶点的度依次为:
| 选项 | |
|---|---|
| A | 2, 1, 1, 1 |
| B | 1, 1, 2, 1 |
| C | 3, 2, 3, 2 |
| D | 2, 3, 2, 3 |
2-32
在下列查找的方法中,平均查找长度与结点个数无关的查找方法是:
| 选项 | |
|---|---|
| A | 顺序查找 |
| B | 二分法 |
| C | 利用散列表 |
| D | 利用二叉搜索树 |
2-33
已知线性表的关键字集合 { 21,11, 13,25,48,6,39,83,30,96,108 },散列函数为 h=key%11,采用分离链接法解决冲突。则成功查找的平均查找长度为:
| 选项 | |
|---|---|
| A | 1.18 |
| B | 1.27 |
| C | 1.36 |
| D | 2.36 |
2-34
输入 1 0 6 10^6 106 个只有一位数字的整数,可以用 O(N) 复杂度将其排序的算法是:
| 选项 | |
|---|---|
| A | 快速排序 |
| B | 桶排序 |
| C | 堆排序 |
| D | 希尔排序 |
2-35
采用递归方式对顺序表进行快速排序,下列关于递归次数的叙述中,正确的是:
| 选项 | |
|---|---|
| A | 递归次数与每次划分后得到的分区处理顺序无关 |
| B | 递归次数与初始数据的排列次序无关 |
| C | 每次划分后,先处理较长的分区可以减少递归次数 |
| D | 每次划分后,先处理较短的分区可以减少递归次数 |
填空题
4-1
下列程序运行输出结果为:5
#include <stdio.h>
int ack(int m, int n);
int main()
{ int m=2, n=1;
printf("%d", ack(m,n));
return 0;
}
int ack(int m, int n)
{ if (m == 0) return n+1;
if (n == 0) return ack(m-1, 1);
return ack(m-1, ack(m, n-1));
}
4-2
下列程序段的输出结果是:28
int i, j, k, count=0;
for(i=0; i<8; i++)
for(j=0; j<i; j++)
if (j%2)
for(k=0; k<j; k++) count++;
else
continue;
printf("%d",count);
4-3
假如下面程序的源程序文件名是 echo.c,编译链接后的可执行程序文件名是 echo.exe,那么执行命令 echo How Are You?的输出是:Good!
#include <stdio.h>
int main(int argc, char *argv[])
{ int k, i=0;
static char s[10]= "Good!";
for(k = 1; k <argc; k++) s[i++] = *(argv[k]+k);
printf("%s", s);
return 0;
}
4-4
给定一棵树的先序遍历序列为 { 1 2 3 4 6 7 5 },后序遍历序列为 { 2 6 7 4 5 3 1 }。
(1)请描述这棵二叉树:
- 根结点是 1
- 3 是根结点的右孩子
- 4 和 5是兄弟结点
- 树中共有 4 个叶结点
(2)请写出该树的中序遍历结果。
2
1
6
4
7
3
5
4-5
给定无向带权图如图所示:
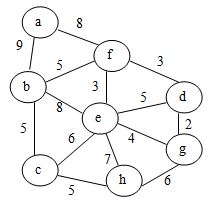
(1) 请给出从顶点 a 出发深度优先搜索遍历该图的顶点序列(多个顶点可以选择时按字母序):
a b c e d f g h
(2) 请给出从顶点g出发广度优先搜索遍历该图的顶点序列(多个顶点可以选择时按字母序):
g d e h f b c a
(3) 请描述最小生成树:
该树的权重是 31 ;树中(填有或无)无 从 e 到 g 的这条边。
程序填空题
5-1 选猴王
一群猴子要选新猴王。新猴王的选择方法是:让 n只候选猴子围成一圈,从某位置起顺序编号为 1~n号。从第 1 号开始报数(从 1 到 4),凡报到 4 的猴子即退出圈子,接着又从紧邻的下一只猴子开始同样的报数。如此不断循环,最后剩下的一只猴子就选为猴王。以下程序采用单循环链表模拟了这个过程,KingOfMonkey函数返回猴王编号。请在空缺处填上正确的代码。
typedef struct node
{ int number; /*猴子的编号*/
struct node *next; /*指向下一只猴子的指针*/
} linklist;
int steps = 4; /*报数到这个定数(正整数),确定下一只出局的猴子*/
linklist *CreateCircle(int n); /*创建有n个编号的无头结点单循环链表*/
int KingOfMonkey(int n, linklist *head);
int main()
{ linklist *head;
int n;
scanf("%d",&n);
if (n>0){
head = CreateCircle(n);
printf("%d\n", KingOfMonkey(n,head));
}
return 0;
}
linklist *DeleteNext(linklist *p) /* 删除单循环链表的p所指的下一个结点 */
{ linklist *s;
if ( p && p->next!=p ) {
s=p->next; //填空处
p->next = s->next;
free(s); return p->next;
}else if (p){
free(p); return NULL;
}else return NULL;
}
int KingOfMonkey(int n,linklist *head)
{ linklist *p = head;
int i, j;
for(j=1; j<=n-1; j++){
for(i=2; i<steps; i++) p=p->next;
p=DeleteNext(p); //填空处
}
return p->number; //填空处
}
5-2 有理数相加
假如有理数类型定义如下:
typedef struct
{ int n; /*numerator,分子,允许是负数*/
int d; /*denominator,分母,大于0;且n和d没有大于1的公因子*/
} RATIONAL;
下面是两个有理数的加法函数 AddR()以及相关的另两个函数代码,请对程序填空。
unsigned int gcd( int x, int y); /*求最大公因子*/
RATIONAL Simplify(RATIONAL a); /*有理数约简,如6/9约简为2/3*/
RATIONAL AddR(RATIONAL a, RATIONAL b) /*有理数相加,如:1/2+2/3=7/6 */
{ RATIONAL t;
a = Simplify(a); b = Simplify(b);
t.n = a.n*b.d+a.d*b.n; //填空处
t.d = a.d * b.d;
return Simplify(t);
}
RATIONAL Simplify(RATIONAL a) /*化简有理数*/
{ RATIONAL t;
int divisor = gcd(a.n,a.d); //填空处
t.n = a.n / divisor;
t.d = a.d / divisor;
return t;
}
unsigned int gcd(int x, int y) /*y>0; 求|x|与y的最大公因子*/
{ int r;
if ( x < 0 ) x = -x;
while(1)
{ r = x % y;
if (r == 0) return y;
x = y;
y=r; //填空处
}
}
5-3 拓扑排序(暂时未知正确答案)
下列代码的功能是对一个给定的图G执行拓扑排序,其中TopNum[]从 1 开始记录拓扑序。请完成程序填空。
void Topsort( Graph G )
{ Queue Q;
Vertex V, W;
NodePtr ptr;
int counter = 0;
Q = CreateEmptyQueue(G->NumV); /*初始化队列*/
for ( V=0; V<G->NumV; V++ )
if ( Indegree[V] == 0 ) /*Indegree[V]记录V的入度*/
Enqueue(V, Q);
while ( !IsEmpty(Q) ){
V = Dequeue( Q );
TopNum[V] = ; //填空处
for ( ptr=G->List[V]; ptr; ptr=ptr->Next) {
W = ptr->Vert;
if () //填空处
Enqueue(W, Q);
}
}
if () //填空处
printf("错误:此图存在环\n");
DisposeQueue(Q);
}
函数题
6-1 有序链表的并集与去重(暂时未知正确答案)
给定两个带头结点的严格降序的链表 L1 和 L2,要求你求两个链表的并集,其中元素仍然严格降序排列,且必须排除重复元素;重复的元素必须链成另一个降序排列的链表。完成去重合并后,并集链表的表头为 L1,重复元素链表的表头为 L2。
例如:L1→头结点→13→10→9→5;L2→头结点→15→10→5→2。
则合并后:L1→头结点→15→13→10→9→5→2;L2→头结点→10→5。
函数接口定义:
void ListUnion( List L1, List L2 )
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
int Key;
PtrToNode Next;
};
typedef PtrToNode List;
要求算法额外空间复杂度为O(1),时间复杂度为O(n)。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef struct Node *PtrToNode;
struct Node {
int Key;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表;空链表将输出NULL */
void ListUnion( List L1, List L2 );
int main()
{
List L1, L2;
L1 = Read();
L2 = Read();
ListUnion(L1, L2);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
4
13 10 9 5
4
15 10 5 2
输出样例:
15 13 10 9 5 2
10 5
参考答案:

来自 @h70208879 大佬的解析,很详细。
























 230
230

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








