动态规划经典例子

数塔问题

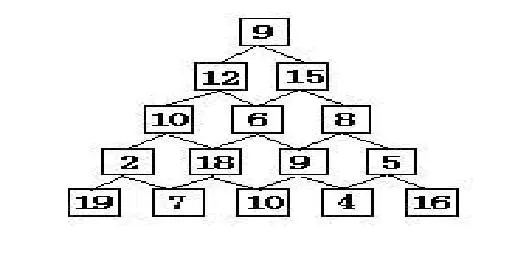
求第一层到最后一层的路径，将该路径上的所有数字相加后得到的和最大是多少。

#include <iostream>
using namespace std;
const int maxn = 1000;
int f[maxn][maxn], dp[maxn][maxn];
int main(){
	
	int n;
	
	cin >> n;  //n为层数
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= i; j++){
			cin >> f[i][j];			//输入数塔
		}
	}
	 
	for(int i = 1; i <= n; i++){
		dp[n][i] = f[n][i];
	}
	
	for(int i = n - 1; i >= 0; i--){
		for(int j = 0; j <= i; j++){
			dp[i][j] = max(dp[i+1][j+1], dp[i+1][j]) + f[i][j];
		}
	}
	
	cout << dp[1][1] << endl;	 //dp[1][1]即为答案
	 
	return 0;
} 

对于数塔问题，贪心法从最上层开始，每次选择坐下和右下两个数字中较大的一个，一直到最底层得到最后结果，显然这不一定可以得到最优解。然而动态规划不管是采用自底向上还是自顶向下，都是从边界开始向上得到目标问题的解。
动态规划总是会考虑所有子问题，并选择继承能得到最优结果的那个，对暂时没被继承的子问题，由于重叠子问题的存在，后期可能会再次考虑它们，因此还有机会成为全局最优的那一部分。
贪心是一种壮士割腕的决策，只要进行了选择，就不后悔；动态规划则要看哪个选择笑到了最后，暂时的领先说明不了什么。

最大连续子序列和

给定一个数字序列a1, a2, a3, … , an。求i，j ( 1 <= i <= j <= n )，使得ai + … + aj 最大， 输出这个最大和。

#include <iostream>
using namespace std;
const int maxn = 10010;
int a[maxn], dp[maxn];
int main(){
	
	int n, ans;
	
	cin >> n;
	
	for(int i = 0; i < n; i++){
		cin >> a[i];
	}
	
	dp[0] = a[0];
	
	ans = 0;
	//dp[i]存放以a[i]结尾的连续序列的最大和，需要遍历i得到最大的才是结果。 
	for(int i = 1; i < n; i++){
		dp[i] = max(dp[i-1] + a[i], a[i]);
		ans = max(dp[i], ans);	//记录最大的dp[i]
	}
	
	cout <<  ans << endl;
	
	return 0;
} 

最长不下降子序列

在一个数字序列中，找到一个最长的子序列（可以不连续），使得这个子序列是不下降（非递减）的。

#include <iostream>
using namespace std;
const int maxn = 10010;
int a[maxn], dp[maxn];
int main(){
	
	int n, ans;
	
	cin >> n;
	
	for(int i = 1; i <= n; i++){
		cin >> a[i];
	}
	  
	ans = 0;	//记录最大的dp[i]
	for(int i = 1; i <= n; i++){
		dp[i] = 1;		
		for(int j = 1; j < i; j++){
			if(a[j] <= a[i] && dp[j] + 1 > dp[i]){
				dp[i] = dp[j] + 1;
			}
		}
		ans = max(dp[i], ans);
	}
		
	cout << ans << endl;
	
	return 0;
} 

最长公共子序列

给定两个字符串（或数字序列）A和B，求一个字符串，使得这个字符串是A和B的最长公共部分（子序列可以不连接）。

#include <iostream>
using namespace std;
const int maxn = 10010;
string a, b;
int dp[maxn][maxn];
int main(){
	 
	cin >> a >> b;
	
	for(int i = 0; i <= a.length(); i++){
		dp[i][0] = 0;
	}
	
	for(int i = 0; i <= b.length(); i++){
		dp[0][i] = 0;
	}
	
	for(int i = 1; i <= a.length(); i++){
		for(int j = 1; j <= b.length(); j++){
			if(a[i] == b[j]){
				dp[i][j] = dp[i-1][j-1] + 1;
			}else{
				dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
			}
		}
	}
	
	cout << dp[a.length()][b.length()];
	
	return 0;
}