2.动规1

最新推荐文章于 2022-07-31 16:17:18 发布

云疏不知数

最新推荐文章于 2022-07-31 16:17:18 发布

阅读量470

点赞数 5

分类专栏：动规如此简单

本文链接：https://blog.csdn.net/qq_43808700/article/details/116137295

版权

动规如此简单专栏收录该内容

5 篇文章 0 订阅

订阅专栏

动规之开门见山

动态规划是分治思想的延申

动态规划具备的特点

把原来的问题分解成几个相似的子问题
所有的子问题都只需要解决一次
按需求存储存储子问题的解

本质

动态规划的本质是，对问题状态的定义和状态转移方程的定义(状态以及状态之间的转移关系)

对子问题的抽象，抽象出来的东西就是状态的定义，状态的定义是不是有效的是不是合理的，可以和最终问题对应起来，看某一个状态能不能对应到问题的解，或者某几个状态它能不能对应到问题的解，如果可以，说明差不多是合理的，需要进一步确认，状态之间能不能形成递推的关系，能不能找到这样的转移方程，状态可以定义出来，方程也可以定义出来，说明是一个比较完美的定义

思考角度

状态定义
状态间的转移方程定义
状态的初始化
返回结果

状态定义的要求：定义的状态一定要形成递推关系

适应场景：最大值、最小值、可不可行、是不是、方案个数

矩形覆盖

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

问题

覆盖一个2*n的大矩形，总共有多少种方法

状态

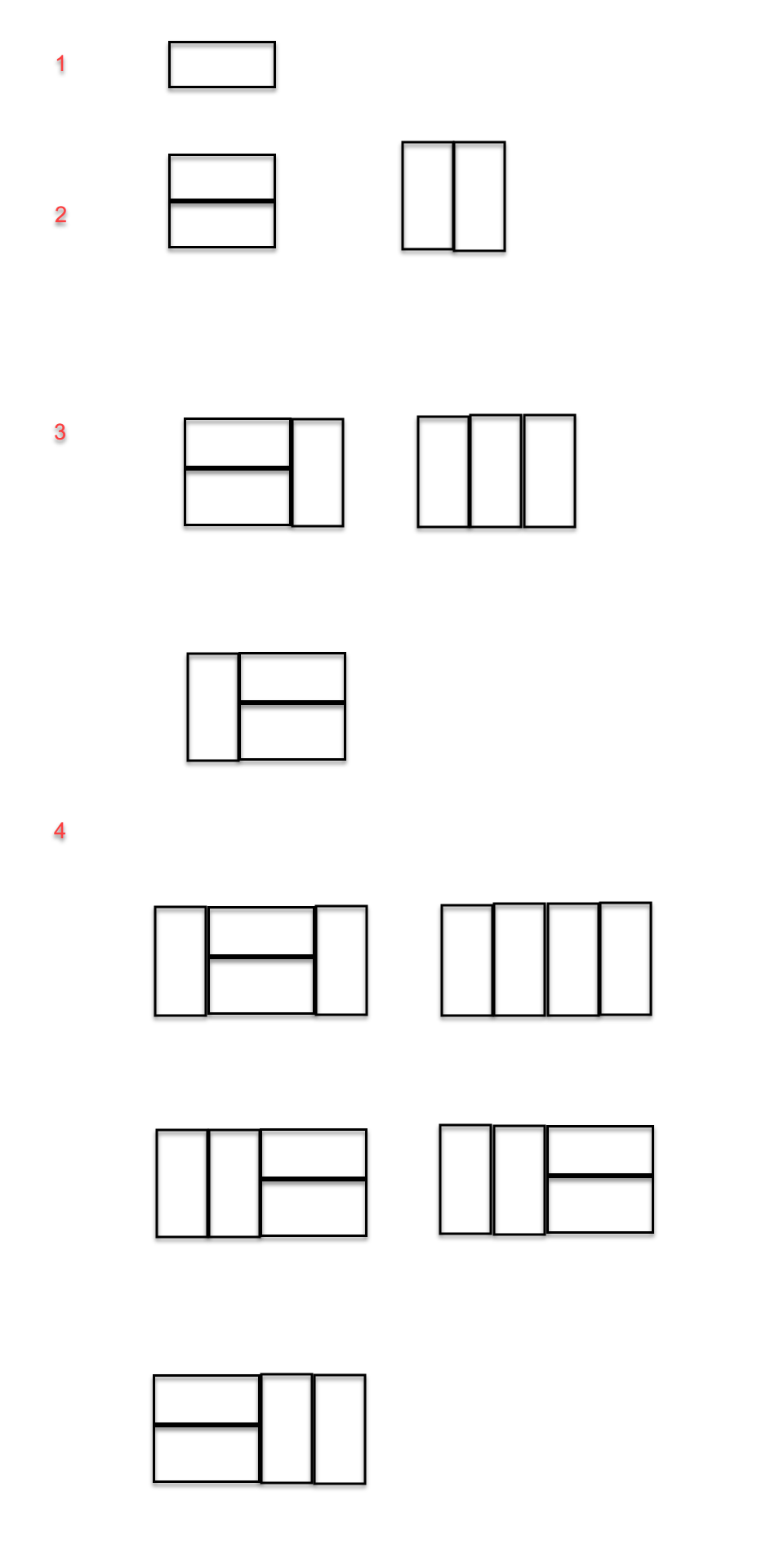
F(1) = 1 = F(0)

F(2) = 2 = F(1) + F(0)

F(3) = 3 = F(2) + F(1)

F(4) = 5 = F(3) + F(2)

铺满2*i的大矩形的方法个数：

F(i) = F(i-1) + F(i-2)

转移方程

F(i) = F(i-1) + F(i-2)

初始状态

F(1) = F(0) = 1

F(n)

代码

都是斐波那契数列，所以参考经典青蛙跳台阶代码相同

这题：注意n=0时返回0

int rectCover(int number) {
    //递归
    if(number<=2) return number;
    return rectCover(number-1)+rectCover(number-2);
    
    //动规
    if(number < 2) return number;
    vector<int> arr(number+1, 0);
    //初始状态 F(0) = F(1) = 1
    arr[0] = arr[1] = 1;
    for(int i=2; i<=number; ++i)
        arr[i] = arr[i-1]+arr[i-2];
    return arr[number];
    
    //迭代
    if(number < 2) return number;
    int cur = 1,pre = 1;
    for(int i=2; i<=number; ++i){
        int tmp = cur;
        cur += pre;
        pre = tmp;
    }
    return cur;
}

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

求最值的问题，可以用动规

问题

数组的最大连续和

子问题：局部元素构成的数组，最大子序列和

状态

到第i个元素的最大子序列和不一定包含第i个元素；

所以状态是以第i个元素结尾的连续最大子序列

转移方程

F(i) = max(F(i-1)+a[i], a[i])

初始状态

子数组知道是一个元素，因此F[0] = a[0]

F[0] = a[0]

max(F[i])

代码

保存中间结果找到所有局部解的最大值

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        if(array.empty())
            return 0;
        //F[0] = a[0]
        vector<int> maxSum(array);
        for(int i=1; i<array.size(); ++i){
            //F[i] = max(F[i-1]+a[i], a[i])
            maxSum[i] = max(maxSum[i-1]+array[i], array[i]);
        }
        //max(F[i])
        int ret = maxSum[0];
        for(int i=1; i<maxSum.size(); ++i){
            ret = max(ret, maxSum[i]);
        }
        return ret;
    }
};

保存中间结果控制到单层循环

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        if(array.empty())
            return 0;
        //F[0] = a[0]
        vector<int> maxSum(array);
        int ret = maxSum[0];
        for(int i=1; i<array.size(); ++i){
            //F[i] = max(F[i-1]+a[i], a[i])
            maxSum[i] = max(maxSum[i-1]+array[i], array[i]);
            //max(F[i])
            ret = max(ret, maxSum[i]);
        }
        return ret;
    }
};

不保存中间结果

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        if(array.empty())
            return 0;
        //F[0] = a[0]
        int ret = array[0];
        for(int i=1; i<array.size(); ++i){
            //F[i] = max(F[i-1]+a[i], a[i])
            array[i] = max(array[i-1]+array[i], array[i]);
            //max(F[i])
            ret = max(ret, array[i]);
        }
        return ret;
    }
};

字符串分割(Word Break)

给定一个字符串s和一组单词dict，判断s是否可以用空格分割成一个单词序列，使得单词序列中所有的单词都是dict中的单词（序列可以包含一个或多个单词）。
例如:
给定s=“nowcode”；
dict=[“now”, “code”].
返回true，因为"nowcode"可以被分割成"now code".

问题

单词是否可以成功分割

子问题：单词的前几个字符是否可以成功分割

状态¹

我们以s=“leetcode”，dict = [“leet”, “code”]为例

F[0] = “l” --> false

F[1] = “le” --> false

F[2] = “lee” --> false

F[3] = “leet” --> true

F[4] = F[4]+“c” --> false

F[5] = F[3]+“co” --> false

F[6] = F[3]+“cod” --> false

F[7] = F[3]+“code” --> true

得出状态：

单词前i个字符可以被成功分割

转移方程

F[i]: j < i && F[j] && substr[j+1,i]是否可以在字典中找到

初始状态

F[0] = substr[0,0]是否可以在字典中找到

F[s.size()-1]

代码

动规C++

class Solution {
public:
    bool wordBreak(string s, unordered_set<string> &dict) {
        bool* F = new bool[s.size()]();
        for (int i = 0; i < s.size(); ++i) {
            //F[0] = substr[0,0]
            //判断整体[0,i]是不是在字典里
            F[i] = (dict.find(s.substr(0, i+1)) != dict.end());
            for (int j = 0; j < i; ++j) {
                //F[j] && substr[j+1,i]是否可以在字典中找到
                if (F[j] && dict.find(s.substr(j + 1, i - j))!= dict.end()) {
                    F[i] = true;
                    break;
                }
            }
        }
        return F[s.size() - 1];
    }
};

动规java

import java.util.Set;
public class Solution {
    public boolean wordBreak(String s, Set<String> dict) {
        boolean[] F = new boolean[s.length()];
        for(int i=0; i<s.length(); ++i){
            //判断[0,i]上str是不是在dict中
            F[i] = dict.contains(s.substring(0, i+1));
            for(int j=0; j<i; ++j){
                //F[j] && [j+1, i]是否可以在字典中找到
                if(F[j] && dict.contains(s.substring(j+1, i+1))){
                    F[i] = true;
                    break;
                }
            }
        }
        return F[s.length()-1];
    }
}

递推关系的一种描述，定义状态的时候，前几次的状态要能被本次以及以后几次的状态中使用 ↩︎

云疏不知数

关注

5
点赞
踩
4

收藏

觉得还不错? 一键收藏
1
评论
2.动规1

动态规划是分治思想的延申动态规划具备的特点把原来的问题分解成几个相似的子问题所有的子问题都只需要解决一次按需求存储存储子问题的解本质动态规划的本质是，对问题状态的定义和状态转移方程的定义(状态以及状态之间的转移关系)对子问题的抽象，抽象出来的东西就是状态的定义，状态的定义是不是有效的是不是合理的，可以和最终问题对应起来，看某一个状态能不能对应到问题的解，或者某几个状态它能不能对应到问题的解，如果可以，说明差不多是合理的，需要进一步确认，状态之间能不能形成递推的关系，能不能找到这样的转移方.
复制链接

扫一扫