算法寒假打卡
用博客来记录寒假期间刷算法题的过程，督促自己刷算法题
主要刷 acwing上的算法题包括下面两部分，算法基础课算法题之前已经刷过95%，再刷一遍就比较快了，提高课没刷过，刷起来会慢一些。
锲而不舍，金石可镂！！！
算法基础课算法题
12.6
acwing785.快速排序
AcWing 787. 归并排序
12.7
AcWing 788. 逆序对的数量(归并排序)
AcWing 789. 数的范围(整数二分)
AcWing 790. 数的三次方根(浮点数二分)
AcWing 791. 高精度加法(大数加大数)
AcWing 792. 高精度减法(大数减大数)
AcWing 793. 高精度乘法(大数乘小数)
AcWing 794. 高精度除法(大数除小数)
AcWing 795. 前缀和(一维前缀和)
AcWing 796. 子矩阵的和(二维前缀和)
AcWing 797. 差分
AcWing 798. 差分矩阵(二维差分)
12.8
AcWing 799. 最长连续不重复子序列(双指针)
AcWing 800. 数组元素的目标和(双指针)
AcWing 816. 判断子序列(双指针)
AcWing 801. 二进制中1的个数(位运算)
AcWing 803. 区间合并(贪心)
AcWing 802. 区间和(离散化)
AcWing 830. 单调栈
AcWing 3302. 表达式求值(模拟)
12.9
AcWing 154. 滑动窗口(单调队列)
AcWing 836. 合并集合(并查集)
AcWing 837. 连通块中点的数量(带权并查集)
12.10
AcWing 831. KMP字符串
AcWing 838. 堆排序
AcWing 839. 模拟堆
AcWing 841. 字符串哈希
AcWing 240. 食物链(并查集)
12.11
AcWing 835. Trie字符串统计(Trie树)
AcWing 143. 最大异或对(Trie树)
AcWing 842. 排列数字(DFS)
AcWing 843. n-皇后问题(DFS)
AcWing 844. 走迷宫(BFS)
12.12
AcWing 845. 八数码(BFS)
AcWing 846. 树的重心
AcWing 848. 有向图的拓扑序列
AcWing 849. Dijkstra求最短路 I(数组存稠密图)
12.13
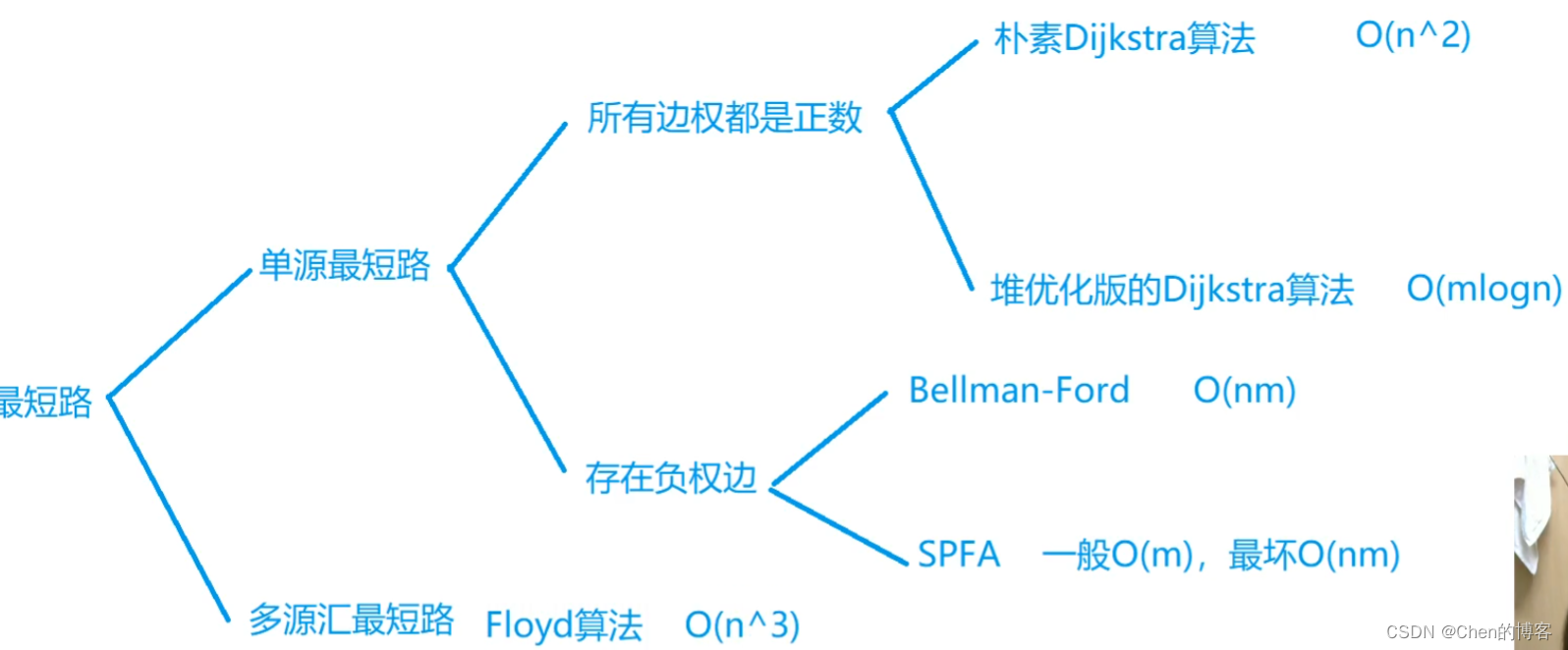在求最短路问题中，有负权回路，最短路不一定存在
可以用Bellman-Ford或者SPFA算法来判断是否有负权回路
AcWing 850. Dijkstra求最短路 II(链式前向星存稀疏图+堆优化)
AcWing 854. Floyd求最短路
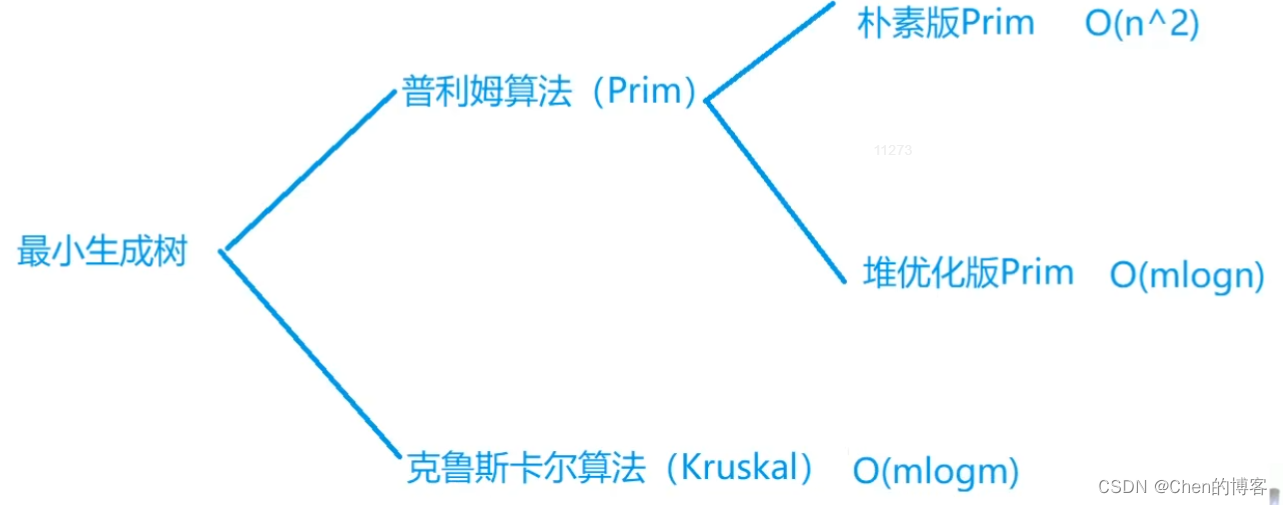
AcWing 858. Prim算法求最小生成树(朴素、堆优化)
AcWing 859. Kruskal算法求最小生成树
AcWing 853. 有边数限制的最短路(Bellman-Ford)
12.14~12.17
身体不适，休息几天
12.18
AcWing 851. spfa求最短路
AcWing 852. spfa判断负环
AcWing 860. 染色法判定二分图
AcWing 861. 二分图的最大匹配(匈牙利算法)
12.19
AcWing 905. 区间选点(左右端点贪心)
AcWing 908. 最大不相交区间数量
AcWing 913. 排队打水
AcWing 104. 货仓选址
AcWing 125. 耍杂技的牛
12.20
AcWing 148. 合并果子
AcWing 906. 区间分组
AcWing 907. 区间覆盖
12.21
AcWing 866. 试除法判定质数
AcWing 867. 分解质因数
AcWing 868. 筛质数(埃氏筛、线性筛)
AcWing 875. 快速幂
AcWing 869. 试除法求约数
AcWing 872. 最大公约数
AcWing 870. 约数个数
AcWing 871. 约数之和
质因子分解：
x
=
p
1
a
1
∗
p
2
a
2
∗
.
.
.
.
.
∗
p
n
a
n
任何一个
x
的约数
y
可以写成
:
y
=
p
1
b
1
∗
p
2
b
2
∗
.
.
.
.
.
∗
p
n
b
n
其中
b
1
∈
0
−
a
1
,
b
2
∈
0
−
a
2
,
.
.
.
.
.
,
b
n
∈
0
−
a
n
根据排列组合可以得到
:
约数个数
=
(
a
1
+
1
)
∗
(
a
2
+
1
)
∗
.
.
.
.
.
∗
(
a
n
+
1
)
约数之和
=
(
p
1
0
+
p
1
1
+
.
.
.
+
p
1
a
1
)
∗
(
p
2
0
+
p
2
1
+
.
.
.
+
p
2
a
2
)
∗
.
.
.
.
.
.
.
∗
(
p
n
0
+
p
n
1
+
.
.
.
+
p
n
a
n
)
x=p_1^{a_1}*p_2^{a_2}*.....*p_n^{a_n}\\ 任何一个x的约数y可以写成: y=p_1^{b_1}*p_2^{b_2}*.....*p_n^{b_n}\\ 其中b_1\in 0-a_1,b_2\in 0-a_2,.....,b_n\in 0-a_n\\ 根据排列组合可以得到:\\ 约数个数=(a_1+1)*(a_2+1)*.....*(a_n+1)\\ 约数之和=(p_1^0+p_1^1+...+p_1^{a_1})*(p_2^0+p_2^1+...+p_2^{a_2})*.......*(p_n^0+p_n^1+...+p_n^{a_n})
x=p1a1∗p2a2∗.....∗pnan任何一个x的约数y可以写成:y=p1b1∗p2b2∗.....∗pnbn其中b1∈0−a1,b2∈0−a2,.....,bn∈0−an根据排列组合可以得到:约数个数=(a1+1)∗(a2+1)∗.....∗(an+1)约数之和=(p10+p11+...+p1a1)∗(p20+p21+...+p2a2)∗.......∗(pn0+pn1+...+pnan)
12.22
1.
费马小定理：如果
p
是一个质数，而整数
a
不是
p
的倍数，则有
a
（
p
−
1
）
≡
1
（
m
o
d
p
）
2.
欧拉定理：若
a
与
p
互质，则有
a
ϕ
(
p
)
≡
1
（
m
o
d
p
）
其中，
1
∼
N
中与
N
互质的数的个数被称为欧拉函数，记为
ϕ
(
N
)
若在算数基本定理中，
N
=
p
1
a
1
p
2
a
2
…
p
n
a
n
，则：
ϕ
(
N
)
=
N
×
(
p
1
−
1
p
1
)
×
(
p
2
−
1
p
2
)
×
…
×
(
p
n
−
1
p
n
)
若一个数
x
为质数，则
ϕ
(
x
)
=
x
−
1
1.费马小定理：如果p是一个质数，而整数a不是p的倍数，则有a^{（p-1）}≡1（mod \ p）\\ 2.欧拉定理：若a与p互质，则有a^{\phi{(p)}}≡1（mod \ p）\\ 其中，1∼N 中与 N 互质的数的个数被称为欧拉函数，记为 ϕ(N)\\ 若在算数基本定理中，N=p_1^{a_1}p_2^{a_2}…p_n^{a_n}，则：\\ ϕ(N) = N×(\frac{p_1−1}{p_1})×(\frac{p_2−1}{p_2})×…×(\frac{p_n−1}{p_n})\\ 若一个数x为质数，则\phi (x)=x-1
1.费马小定理：如果p是一个质数，而整数a不是p的倍数，则有a（p−1）≡1（mod p）2.欧拉定理：若a与p互质，则有aϕ(p)≡1（mod p）其中，1∼N中与N互质的数的个数被称为欧拉函数，记为ϕ(N)若在算数基本定理中，N=p1a1p2a2…pnan，则：ϕ(N)=N×(p1p1−1)×(p2p2−1)×…×(pnpn−1)若一个数x为质数，则ϕ(x)=x−1
AcWing 873. 欧拉函数
AcWing 874. 筛法求欧拉函数(线性筛)
AcWing 876. 快速幂求逆元
12.23
裴蜀定理：对于任意正整数a,b，一定存在整数x,y,使得
ax + by=gcd (a , b)
AcWing 877. 扩展欧几里得算法
AcWing 878. 线性同余方程
12.24
AcWing 883. 高斯消元解线性方程组
AcWing 884. 高斯消元解异或线性方程组
12.25~12.29
消化一下这几天学的数论方面知识+放假回家=休息几天
12.30
中国剩余定理
AcWing 204. 表达整数的奇怪方式
组合数
C
a
0
=
C
a
a
=
C
0
0
=
1
C_a^0=C_a^a=C_0^0=1
Ca0=Caa=C00=1
C
a
b
=
a
!
b
!
(
a
−
b
)
!
C_a^b=\frac{a!}{b!(a-b)!}
Cab=b!(a−b)!a!
C
a
b
=
C
a
a
−
b
C_a^b=C_a^{a-b}
Cab=Caa−b
C
a
b
=
C
a
−
1
b
−
1
+
C
a
b
−
1
C_a^b=C_{a-1}^{b-1}+C_a^{b-1}
Cab=Ca−1b−1+Cab−1
理解：
C
a
b
C_a^b
Cab为从a中选b个的方案数，可将其分为两种情况，选x和不选x（x在a中）。
若选x，则从剩下的a-1中选b-1，方案数为
C
a
−
1
b
−
1
C_{a-1}^{b-1}
Ca−1b−1;
若不选x，则从剩下的a-1中选b，方案数为
C
a
−
1
b
C_{a-1}^{b}
Ca−1b
所以从a中选b的总方案数为
C
a
b
=
C
a
−
1
b
−
1
+
C
a
b
−
1
C_a^b=C_{a-1}^{b-1}+C_a^{b-1}
Cab=Ca−1b−1+Cab−1
AcWing 885. 求组合数 I(递推)
a的逆元为x (mod p)
b的逆元为y(mod p)
p为质数，且ab%p!=0
ab的逆元为x*y（mod p）
AcWing 886. 求组合数 II(求逆元)
12.31
Lucas定理：Lucas定理是用来求
C
a
b
m
o
d
p
C_a^b mod\ p
Cabmod p ，p为素数的值。
C
a
b
%
p
=
C
a
p
b
p
∗
C
a
%
p
b
%
p
%
p
C_a^b\ \%\ p=C_{\frac{a}{p}}^{\frac{b}{p}}*C_{a\%p}^{b\%p}\%p
Cab % p=Cpapb∗Ca%pb%p%p
AcWing 887. 求组合数 III(lucas+逆元)
1.1~
看论文不定时打卡，距离过年还有21天，今年过年挺早的，算法基础课的题还有25道没刷，计划在过年前将这些题都给刷了，年前结束算法基础课，年后开始提高课刷题。
1.3
AcWing 888. 求组合数 IV(阶乘质因子分解+高精度乘法)
卡特兰数：
C
2
n
n
−
C
2
n
n
+
1
=
C
2
n
n
n
+
1
C_{2n}^{n}-C_{2n}^{n+1}=\frac{C_{2n}^{n}}{n+1}
C2nn−C2nn+1=n+1C2nn
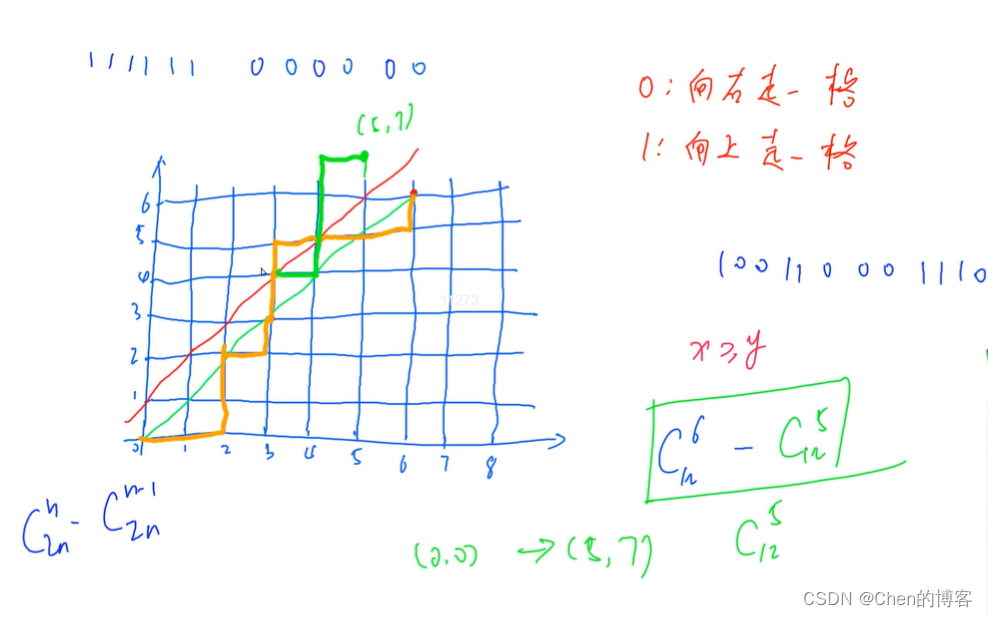
AcWing 889. 满足条件的01序列(卡特兰数)
1.5
AcWing 2. 01背包问题
AcWing 3. 完全背包问题
AcWing 895. 最长上升子序列
AcWing 896. 最长上升子序列 II
1.6
AcWing 898. 数字三角形
AcWing 897. 最长公共子序列
AcWing 901. 滑雪
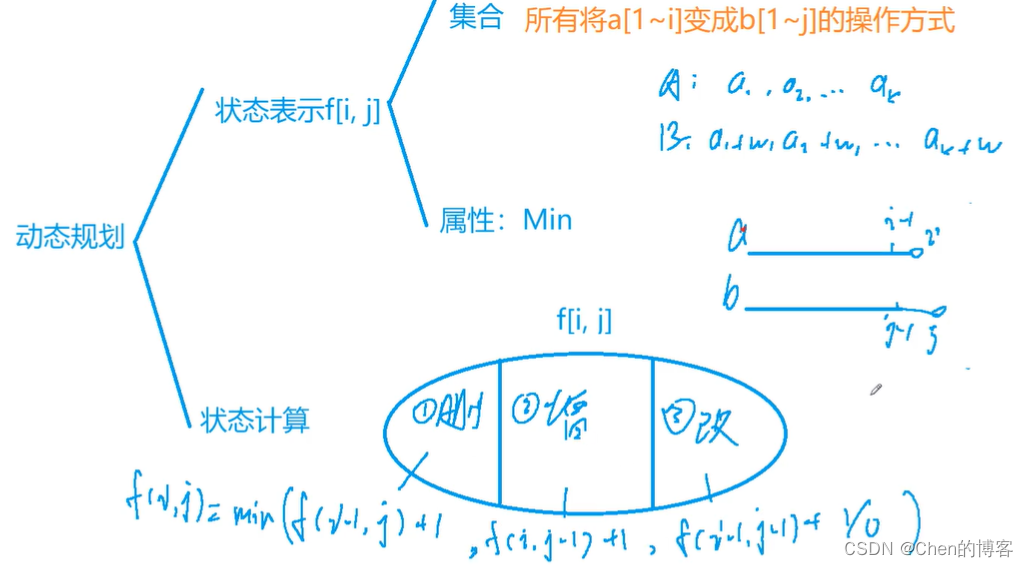
AcWing 902. 最短编辑距离
AcWing 899. 编辑距离
1.7
AcWing 4. 多重背包问题
AcWing 5. 多重背包问题 II(二进制优化)
AcWing 9. 分组背包问题
AcWing 282. 石子合并
AcWing 890. 能被整除的数(容斥原理)
Nim游戏
AcWing 891. Nim游戏
AcWing 892. 台阶-Nim游戏
AcWing 893. 集合-Nim游戏
AcWing 894. 拆分-Nim游戏
1.11
接下来的时间我需要汇报论文，争取年前将题刷完剩下的算法题！！！
1.18
AcWing 900. 整数划分(计数类DP)
整数划分题解
1.19
x=0时需要特殊处理，当x=0时，上面情况的第二步没有问题，第一步需要考虑前导0的情况，从1开始枚举。
AcWing 338. 计数问题(数位DP)
1.20
AcWing 291. 蒙德里安的梦想(状压DP)
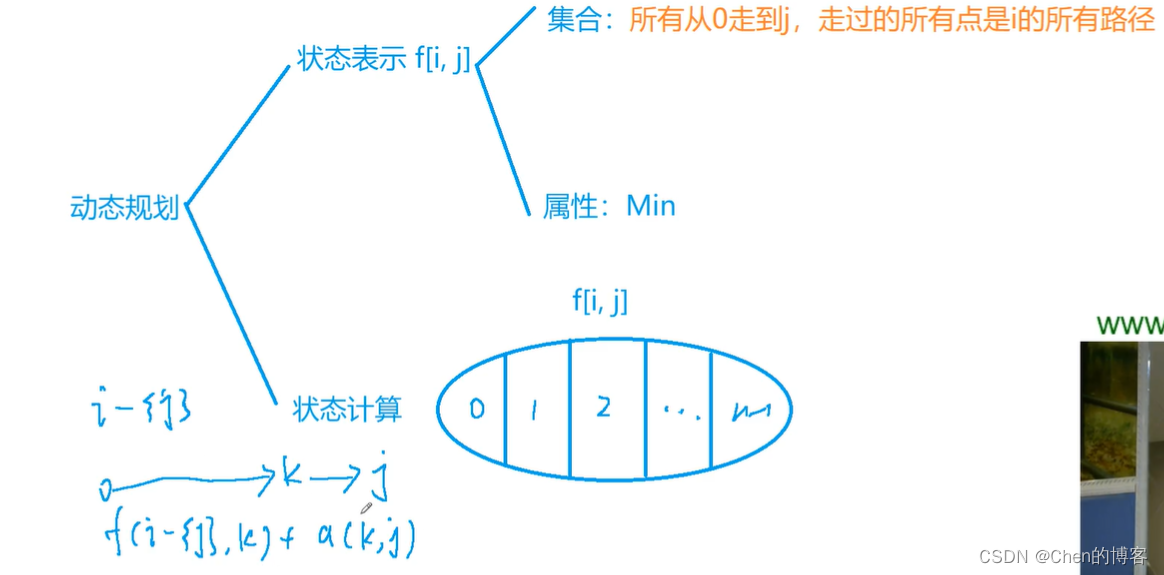
AcWing 91. 最短Hamilton路径(状压DP)
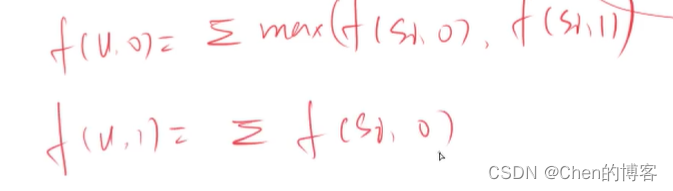
AcWing 285. 没有上司的舞会(树形DP)
算法基础课打卡完成！！！
休息几天，过年走亲戚
240
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
