【吐血整理】数据库重点知识总结【2】

本文是数据库专栏【吐血整理】系列的第二篇，以介绍关系数据库为主，欢迎阅读~

---

一、关系数据结构及形式化定义

1. 关系

关系： 单一的数据结构
现实世界的实体及实体间的各种联系均用关系来表示
二维表： 逻辑结构
从用户角度，关系模型中数据的逻辑结构是一张二维表

①域（Domain）
域（Domain）： 域是一组具有相同数据类型的值的集合。
例如：整数、所有球类的集合，指定长度的字符串集合、{‘男人’，‘女人’} …

②笛卡尔积（Cartesian Product）
笛卡尔积（Cartesian Product）：
给定一组域D₁，D₂，…，D_n，允许其中某些域是相同的
D₁，D₂，…，D_n的笛卡尔积为：
D₁×D₂×…×D_n ＝ ｛（d₁，d₂，…，d_n）｜$di\in Di$，i＝1，2，…，n｝

总结一下： 笛卡尔积就是所有域的所有取值的一个组合（即全集），不能重复

举个栗子哈：
假设集合A={D，B}，集合B={1，2，3}，两个集合的笛卡尔积为：
AXB={(D，1)，(D，2)，(D，3)，(B，1)，(B，2)，(B，3)}

• 不会写下标和上标的小伙伴注意啦！
  下标这样写：~下标~ 效果：_下标
  上标这样写：^上标^ 效果：^上标
  咳咳，可爱的人是不会白嫖的~（暗示点赞关注！）

· 元组（Tuple）：
笛卡尔积中每一个元素（d₁，d₂，…，d_n）叫作一个n元组（n-tuple）或简称元组
例如：在AXB={(D，1)，(D，2)，(D，3)，(B，1)，(B，2)，(B，3)}中，每一个(D，1)，(D，2)… 都是2元组
· 分量（Component）：
笛卡尔积元素（d₁，d₂，…，d_n）中的每一个值 d_i 叫作一个分量
例如：刚刚的例子中 D，B，1，2，3 都是分量
· 基数（Cardinal number）：
若D_i（i＝1，2，…，n）为有限集，其基数为m_i（i＝1，2，…，n），则D₁XD₂X…XD_n的基数M为：

$M={\prod }_{i=i}^n{m}_i$ （即基数的累乘）

可理解为：基数就是集合中的元素的个数
例如：集合A={D，B}基数为2，集合B={1，2，3}基数为3，AXB={(D，1)，(D，2)，(D，3)，(B，1)，(B，2)，(B，3)}的基数为2×3=6

③关系（Relation）
1） 关系
D₁XD₂X…XD_n的 子集 叫作在域D₁，D₂，…，D_n上的关系，表示为:
R（D₁，D₂，…，D_n）
R 是关系名，n 是关系的目或度
例如：COUPLE(BOY，GIRL)，R=COUPLE ，n=2
2）关系的表示
关系是一个二维表
表的每行对应一个元组，表的每列对应一个属性
3）码（Key）

• 候选码：
  若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为候选码。
  简单的情况：候选码只包含一个属性
  最极端的情况：所有属性组是候选码，称为全码
• 主码（PK）：
  若一个关系有多个候选码，则选定其中一个为主码（一般用下划线来表示该候选码为主码）
• 主属性：
  候选码的诸属性称为主属性。
  不包含在任何侯选码中的属性称为非主属性或非码属性

值得注意的是： D₁，D₂，…，D_n的笛卡尔积（全集） 的某个子集（即关系） 才 有实际含义。

三类关系：
· 基本关系（基本表或基表）
实际存在的表，是实际存储数据的逻辑表示
· 查询表
查询结果对应的表（暂存在内存）
· 视图表
由基本表或其他视图表导出的表，是虚表，不对应实际存储的数据
基本关系的性质
① 列是同质的
② 不同的列可出自同一个域

其中的每一列称为一个属性
不同的属性要给予不同的属性名

③ 列的顺序无所谓，列的次序可以任意交换
④ 任意两个元组的候选码不能相同
⑤ 行的顺序无所谓，行的次序可以任意交换
⑥ 分量必须取原子值，这是规范条件中最基本的一条

2. 关系模式

关系模式------------型
· 对关系的描述
· 静态的、稳定的

关系------------------值
· 关系模式在某一时刻的状态或内容
· 动态的、不断变化的

• 关系模式是对关系的描述，可以形式化地表示为：
  R（U，D，DOM，F）
  R： 关系名
  U：组成该关系的属性名集合
  D：U中属性所来自的域
  DOM：属性向域的映象的集合
  F：属性间数据的依赖关系的集合

举个栗子:
篮球（BASKETBALL）和足球（FOOTBALL）出自同一个域——球（BALL），

在模式中定义属性向域的映像，说明它们分别出自哪个域：
DOM（BASKETBALL）
= DOM（FOOTBALL）
= BALL

关系模式通常可以简记为：
R (U) 或 R (A1，A2，…，An)

• R: 关系名
• A1，A2，…，An : 属性名（U是属性名的集合）

关系模式和关系往往笼统称为关系，通过上下文加以区别

3. 关系数据库

在一个给定的应用领域中，所有关系的集合构成一个关系数据库

关系数据库的型：
· 关系数据库模式，是对关系数据库的描述

关系数据库的值：
· 关系模式在某一时刻对应的关系的集合，通常称为关系数据库

4. 关系模型的存储结构

关系数据库的物理组织

• 有的RDBMS中一个表对应一个操作系统文件，将物理数据组织交给操作系统完成
• 有的RDBMS从操作系统那里申请若干个大的文件，自己划分文件空间，组织表、索引等存储结构，并进行存储管理
  ps：关系数据库管理系统（Relational Database Management System：RDBMS）

---

二、关系操作

基本的关系操作

查询：
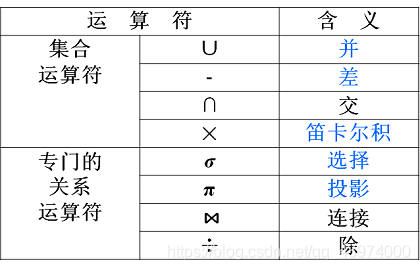
选择、投影、连接、除、并、差、交、笛卡尔积
（选择、投影、并、差、笛卡尔基是5种基本操作，下文的关系代数部分详细讲解）
更新：插入、删除、修改

关系数据库语言的分类

关系代数语言

关系演算语言（元组关系演算语言和域关系演算语言）

具有关系代数和关系演算双重特点的语言
代表：SQL（Structured Query Language）

---

三、关系的完整性

1. 实体完整性

实体完整性规则（Entity Integrity）
· 若属性A是基本关系R的主属性，则属性A不能取空值
ps：空值就是“不知道”或“不存在”或“无意义”的值

比如：选修课（学号，课程号，成绩）
“学号、课程号”为主码
“学号”和“课程号”两个属性都不能取空值

可以简单记忆为：主属性不能为空

2. 参照完整性

关系间的引用
在关系模型中实体及实体间的联系都是用关系来描述的
比如：学生实体、专业实体（主码用下划线表示）
学生（学号，姓名，性别，专业号，年龄）
专业（专业号，专业名）
这个例子中： 学生关系引用了专业关系的主码 “专业号”
学生关系中的 “专业号”值必须是 确实存在的专业的专业号

外码（Foreign Key）
设F是基本关系R的一个或一组属性，但不是关系R的码（ps：码可唯一确定一个元组）。如果F与基本关系S的主码K_s相对应，则称F是R的外码
· 基本关系R称为参照关系（Referencing Relation）
· 基本关系S称为被参照关系（Referenced Relation）
咱通过例子来理解一下：

“专业号”属性F是学生关系的外码
专业关系S是被参照关系，学生关系R为参照关系

参照完整性规则
若属性（或属性组）F是基本关系R的外码它与基本关系S的主码K_s 相对应，则对于R中每个元组在F上的值必须为：

• 要么取空值（F的每个属性值均为空值）
• 要么等于S中某个元组的主码值

简单记忆：外码要么为空，要么源自于被参照关系的主码

3. 用户定义的完整性

针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求
关系模型应提供定义和检验这类完整性的机制，以便用统一的系统的方法处理它们，而不需应用程序承担这一功能。
比如： 课程（课程号，课程名，学分）
· “课程号”属性必须取唯一值
· 非主属性“课程名”不能取空值
· “学分”属性只能取值{0.5，1.0，1.5，2.0，2.5，3.0}

---

四、关系代数

关系代数：一种抽象的查询语言，用对关系的运算来表达查询。

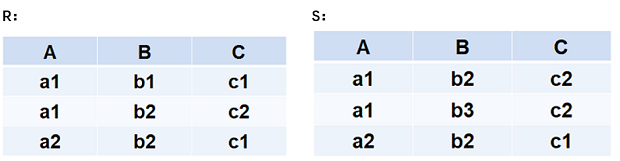
传统的集合运算

R∪S R - S R ∩ S 如下图所示：


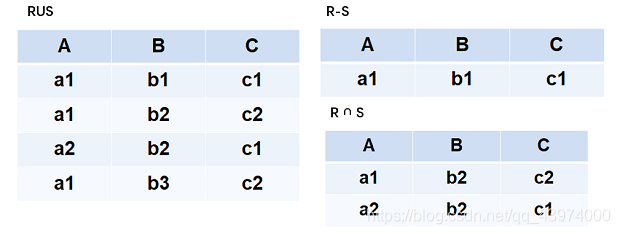
笛卡尔积（Cartesian Product）
严格地讲应该是广义的笛卡尔积
R: n目关系，k₁ 个元组（可理解为R有n列，k₁行）
S: m目关系，k₂ 个元组（可理解为S有m列，k₂行）

R X S

• 列：(n+m）列元组的集合
  元组的前n列是关系R的一个元组
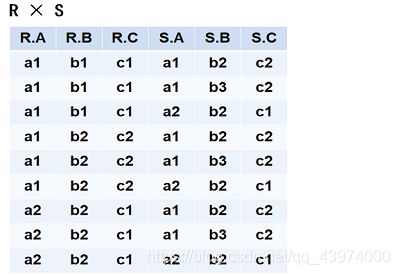
  后m列是关系S的一个元组
• 行： k₁ X k₂个元组（基数）
• 即相当于用R的每一行去和S的每一行“拼”起来，看下图可形象理解

如图所示（3+3=6列，3*3=9行）：

专门的关系运算

1. 选择（Selection）σ
选择 运算符的含义:
在关系R中选择满足给定条件的诸元组
${\sigma }_F\left(R\right)$