最优化方法总结（最不全版）

一、最优化方法简介

最优化方法是研究在给定约束条件下如何寻求最优解的数学理论与技术。它广泛应用于机器学习、工程设计、资源分配等领域，例如深度学习中通过优化损失函数训练模型，工业中通过优化生产流程降低成本。常见的最优化方法可分为传统数学方法（如梯度下降、牛顿法）和智能优化算法（如遗传算法、模拟退火），每种方法在收敛速度、适用场景和实现复杂度上各有特点

二、经典最优化方法解析

1. 梯度下降法（Gradient Descent）

原理与分类

梯度下降法是最基础的优化方法，其核心思想是沿着目标函数的负梯度方向更新参数，以最快速度降低损失。根据每次迭代使用的数据量不同，可分为：

• 批量梯度下降（BGD）：使用全部样本计算梯度（收敛稳定但速度慢）。小批量梯度下降在实际应用中得到广泛使用，它通过平衡计算效率和梯度估计的稳定性，有效减少了随机梯度下降的噪声影响，同时相比批量梯度下降大大提升了训练速度。 例如在深度学习模型训练中，MBGD 常被用于调整神经网络的权重参数，以降低模型的预测误差。通过合理设置批量大小，既能够利用矩阵运算的高效性，又能避免因样本选择随机性过大导致的训练不稳定。 在图像识别、自然语言处理等复杂场景中，MBGD的优势进一步凸显。通过将训练数据划分为多个小批量，模型能够在每次迭代时从不同的数据子集学习特征，增强了模型的泛化能力，同时减少了内存占用，使得在有限计算资源下也能高效训练大规模模型。 此外，在实际使用MBGD时，批量大小的选择至关重要。过小的批量可能导致训练过程过于嘈杂，难以收敛；而过大的批量虽然能使训练更加稳定，但会增加内存需求，降低计算效率。通常需要通过实验，结合数据集规模和硬件资源，在稳定性和效率之间找到最佳平衡点。 ​

• 随机梯度下降（SGD）：每次随机选一个样本（速度快但噪声大）。此外，MBGD还支持学习率衰减策略，随着训练迭代次数增加逐渐降低学习率，使得模型在训练初期能够快速收敛，接近最优解时又能避免因步长过大而跳过最优解，进一步提升了优化效果。 除了学习率衰减，在实际应用MBGD时，还可结合早停策略，当验证集上的损失不再降低时提前终止训练，避免过拟合；也能使用自适应学习率调整算法，如Adagrad、Adadelta等，进一步提升优化性能。

• 小批量梯度下降（MBGD）：折中方案，取批量样本（常用）。除了上述策略，在实际运用小批量梯度下降时，还可以结合梯度裁剪技术，防止梯度爆炸导致训练不稳定。同时，通过调整迭代次数和优化目标函数的正则化参数，也能有效提升模型性能，使其在不同规模和复杂度的数据集上发挥最佳效果。 此外，结合动量（Momentum）或自适应学习率策略的小批量梯度下降变种，如带动量的MBGD和Adam+MBGD，在复杂神经网络训练中表现更优，能够有效加速收敛并避免陷入局部最优。

代码示例（MBGD）

import numpy as np

def mbgd(X, y, learning_rate=0.01, batch_size=32, epochs=100):
    m, n = X.shape
    theta = np.zeros(n)
    for epoch in range(epochs):
        indices = np.random.permutation(m)
        X_batch = X[indices[:batch_size]]
        y_batch = y[indices[:batch_size]]
        gradient = (1/batch_size) * X_batch.T.dot(X_batch.dot(theta) - y_batch)
        theta -= learning_rate * gradient
    return theta

# 示例：线性回归拟合y=2x+1
X = np.random.rand(1000, 1)
X = np.hstack([np.ones((1000, 1)), X])  # 添加截距项列
y = 2 * X[:, 1] + 1 + np.random.normal(0, 0.1, 1000)  # y为一维数组

theta_opt = mbgd(X, y)
print("最优参数:", theta_opt.flatten())  # 接近 [1, 2]

2. 牛顿法与拟牛顿法

牛顿法

牛顿法通过二阶泰勒展开近似目标函数，利用 Hessian 矩阵的逆矩阵确定搜索方向，收敛速度快但计算复杂。阻尼牛顿法通过引入步长因子提高稳定性。在实际应用中，牛顿法虽然理论上具有出色的收敛速度，但由于Hessian矩阵计算和求逆的复杂性，常适用于变量规模较小、目标函数二阶导数计算相对容易的场景。为了克服计算量过大的问题，许多改进版本应运而生，如拟牛顿法，通过近似Hessian矩阵减少计算开销，在保证一定收敛效率的同时，显著提升了算法的实用性和可扩展性。

优点：二次函数只需一步收敛，非二次函数收敛速度快（平方收敛）缺点：Hessian 矩阵求逆计算量大（O (n³)），需正定

拟牛顿法（BFGS 算法）

拟牛顿法通过正定矩阵近似 Hessian 矩阵的逆，避免直接计算 Hessian 矩阵。BFGS 算法是最常用的拟牛顿法之一，其迭代公式为(不会插公式，就放图片吧)：

代码示例

import numpy as np


def newton_method(f, grad, hess, x0, max_iter=100, tol=1e-6):
    x = x0.astype(np.float64)  
    for _ in range(max_iter):
        g = grad(x).astype(np.float64)  
        h = hess(x).astype(np.float64)  
        alpha = 1.0  # 明确使用浮点数

        # 计算更新方向
        try:
            step = np.linalg.inv(h).dot(g)
        except np.linalg.LinAlgError:
            step = np.linalg.pinv(h).dot(g)  
        # Armijo线搜索
        while f(x - alpha * step) > f(x) - 1e-4 * alpha * np.linalg.norm(g) ** 2:
            alpha *= 0.5
            if alpha < 1e-10:  # 防止无限循环
                break
        x -= alpha * step

        if np.linalg.norm(g) < tol:
            break
    return x


# 目标函数及梯度/Hessian（显式指定浮点类型）
f = lambda x: x[0] ** 2 + 2 * x[1] ** 2
grad = lambda x: np.array([2.0 * x[0], 4.0 * x[1]], dtype=np.float64)  
hess = lambda x: np.array([[2.0, 0.0], [0.0, 4.0]], dtype=np.float64)  

# 初始点明确为浮点类型
x_opt = newton_method(f, grad, hess, x0=np.array([3, 2], dtype=np.float64))
print("最优解:", x_opt)  # 输出接近 [0.0, 0.0]

3. 共轭梯度法

共轭梯度法用于求解大型线性方程组和无约束优化问题，通过构造共轭方向避免矩阵求逆。其核心步骤包括：

1. 初始化搜索方向为负梯度方向。
2. 计算步长并更新参数。
3. 利用共轭条件更新搜索方向。

代码示例

import numpy as np  

def conjugate_gradient(A, b, x0, tol=1e-6, max_iter=100):
    x = x0.astype(np.float64) 
    r = b - A.dot(x)
    p = r.copy()
    for _ in range(max_iter):
        Ap = A.dot(p)
        alpha = np.dot(r, r) / np.dot(p, Ap)
        x += alpha * p
        r_new = r - alpha * Ap
        if np.linalg.norm(r_new) < tol:
            break
        beta = np.dot(r_new, r_new) / np.dot(r, r)
        p = r_new + beta * p
        r = r_new
    return x

# 示例：求解Ax = b（显式指定浮点类型）
A = np.array([[2, 1], [1, 3]], dtype=np.float64)
b = np.array([1, 2], dtype=np.float64)
x0 = np.array([0, 0], dtype=np.float64)

x_opt = conjugate_gradient(A, b, x0)
print("最优解:", x_opt)  # 应输出接近 [0.2, 0.6]

三、约束优化：处理带约束问题

1. 拉格朗日乘数法（Lagrange Multipliers）​

适用场景：等式约束优化问题原理：引入拉格朗日乘子将约束融入目标函数，转化为无约束问题

KKT 条件（扩展到不等式约束）：

• 原约束：gi​(θ)≤0在实际应用中，拉格朗日乘数法需确保约束函数和目标函数满足一定的正则条件，才能保证KKT条件是最优解的充要条件。对于复杂的约束优化问题，常结合数值迭代算法求解拉格朗日函数的鞍点，通过不断调整拉格朗日乘子和决策变量，逐步逼近最优解。 同时，KKT条件中的互补松弛条件为判断约束是否起作用提供了依据，在实际建模和求解中，可通过该条件简化问题，识别出真正有效的约束，从而降低计算复杂度。 ​
• 对偶约束：λi​≥0

• ​互补松弛：λi​gi​(θ)=0

import numpy as np
from scipy.optimize import minimize

def lagrange_multipliers_optimization():
    # 定义目标函数和约束条件
    def objective(x):
        return x[0]**2 + x[1]**2  # 示例目标函数：f(x1, x2) = x1² + x2²

    # 等式约束：h(x) = x1 + x2 - 1 = 0
    def eq_constraint(x):
        return x[0] + x[1] - 1

    # 不等式约束：g(x) = x1 - 0.5 ≤ 0
    def ineq_constraint(x):
        return x[0] - 0.5

    # 构建拉格朗日函数（含KKT条件）
    def lagrangian(x, λ_eq, λ_ineq):
        return objective(x) + λ_eq * eq_constraint(x) + λ_ineq * ineq_constraint(x)

    # 初始猜测值
    x0 = np.array([0.0, 0.0])
    λ0_eq = 0.0
    λ0_ineq = 0.0

    # 使用SciPy的SLSQP算法求解（内置处理KKT条件）
    constraints = [
        {'type': 'eq', 'fun': eq_constraint},
        {'type': 'ineq', 'fun': ineq_constraint}
    ]
    result = minimize(objective, x0, method='SLSQP', constraints=constraints)
    
    return result.x, result

# 运行示例
x_opt, result = lagrange_multipliers_optimization()
print("最优解:", x_opt)
print("验证约束:")
print(f"等式约束 x1 + x2 - 1 = {x_opt[0] + x_opt[1] - 1:.6f}")
print(f"不等式约束 x1 - 0.5 = {x_opt[0] - 0.5:.6f}")

# 输出应接近 [0.5, 0.5]，满足约束

2. 序列最小优化（SMO，用于 SVM）​

SMO 是由 John Platt 在 1998 年提出的，用于高效解决 SVM 中的二次规划问题。传统的二次规划算法在处理大规模数据时效率低下，而 SMO 通过分解问题为多个小的二次规划子问题，每次优化两个变量，从而显著提高了计算速度。

优点：

1. 无需存储大规模矩阵，内存效率高
2. 解析解推导避免迭代优化，速度快
3. 适合处理线性可分及近似可分问题

缺点

1. 对噪声敏感（需配合软间隔参数C调整）
2. 非线性核场景下计算复杂度随样本量增长
3. 需仔细调优启发式策略

核心思想：分解大规模二次规划问题为最小子问题，每次优化两个变量代码简化版（基于 libsvm 原理）：

import numpy as np

class SMO:
    def __init__(self, C=1.0, tol=1e-3, max_iter=1000):
        self.C = C
        self.tol = tol
        self.max_iter = max_iter

    def fit(self, X, y):
        self.X = X  # 保存训练数据
        self.y = y   # 保存标签
        m, n = X.shape
        alpha = np.zeros(m)
        b = 0.0
        for _ in range(self.max_iter):
            num_changed = 0
            for i in range(m):
                # 计算样本i的误差
                E_i = self._predict(alpha, b, i) - y[i]
                
                # 检查KKT条件是否违反
                if (y[i] * E_i < -self.tol and alpha[i] < self.C) or \
                   (y[i] * E_i > self.tol and alpha[i] > 0):
                    
                    # 选择第二个变量j：寻找误差差异最大的样本
                    j = self._select_second_alpha(i, alpha, b)
                    if j == -1:  # 无法找到有效j
                        continue
                    
                    # 计算样本j的误差
                    E_j = self._predict(alpha, b, j) - y[j]
                    
                    # 计算上下界
                    if y[i] != y[j]:
                        L = max(0, alpha[j] - alpha[i])
                        H = min(self.C, self.C + alpha[j] - alpha[i])
                    else:
                        L = max(0, alpha[i] + alpha[j] - self.C)
                        H = min(self.C, alpha[i] + alpha[j])
                    if L == H:
                        continue
                    
                    # 计算eta（核函数为线性）
                    eta = self.X[i].dot(self.X[i]) + self.X[j].dot(self.X[j]) - 2 * self.X[i].dot(self.X[j])
                    if eta <= 0:
                        continue
                    
                    # 更新alpha[j]
                    alpha_j_old = alpha[j]
                    alpha[j] += y[j] * (E_i - E_j) / eta
                    alpha[j] = np.clip(alpha[j], L, H)
                    
                    # 检查alpha[j]变化量是否足够小
                    if abs(alpha[j] - alpha_j_old) < 1e-5:
                        continue
                    
                    # 更新alpha[i]
                    alpha[i] += y[i] * y[j] * (alpha_j_old - alpha[j])
                    
                    # 更新偏置项b
                    b1 = b - E_i - y[i] * (alpha[i] - alpha[i]) * self.X[i].dot(self.X[i]) \
                         - y[j] * (alpha[j] - alpha_j_old) * self.X[i].dot(self.X[j])
                    b2 = b - E_j - y[i] * (alpha[i] - alpha[i]) * self.X[i].dot(self.X[j]) \
                         - y[j] * (alpha[j] - alpha_j_old) * self.X[j].dot(self.X[j])
                    if 0 < alpha[i] < self.C:
                        b = b1
                    elif 0 < alpha[j] < self.C:
                        b = b2
                    else:
                        b = (b1 + b2) / 2
                    num_changed += 1
            if num_changed == 0:
                break
        self.alpha = alpha
        self.b = b

    def _predict(self, alpha, b, i):
        """计算第i个样本的预测值"""
        return np.dot(alpha * self.y, np.dot(self.X, self.X[i])) + b

    def _select_second_alpha(self, i, alpha, b):
        """选择第二个变量j的启发式方法"""
        m = self.X.shape[0]
        max_error_diff = -1
        j = -1
        E_i = self._predict(alpha, b, i) - self.y[i]
        for k in range(m):
            if k == i:
                continue
            E_k = self._predict(alpha, b, k) - self.y[k]
            error_diff = abs(E_i - E_k)
            if error_diff > max_error_diff:
                max_error_diff = error_diff
                j = k
        return j

# 示例：二维线性可分数据
X = np.array([[1, 2], [2, 3], [3, 1], [4, 2]], dtype=np.float64)
y = np.array([1, 1, -1, -1], dtype=np.float64)
smo = SMO(C=1.0, tol=1e-3, max_iter=100)
smo.fit(X, y)
print("支持向量系数:", smo.alpha[smo.alpha > 1e-5])
print("偏置项b:", smo.b)

 

四、智能优化算法

1. 遗传算法（Genetic Algorithm，GA）

遗传算法通过模拟生物进化过程中的自然选择、遗传和变异机制，在解空间中进行高效搜索，特别适用于传统数学方法难以求解的复杂优化问题，如组合优化、路径规划等。 在每一代进化过程中，遗传算法通过上述步骤不断筛选、进化种群，随着迭代次数的增加，种群逐渐向最优解靠近。该算法的优势在于其全局搜索能力，对目标函数的连续性和可导性没有严格要求，能够在复杂的解空间中探索到较优解。步骤包括：

1. 初始化种群：随机生成初始解（染色体）​

1. 适应度评估：计算每个个体的适应度（目标函数值）​

1. 选择：轮盘赌 / 锦标赛选择优质个体​

1. 交叉：单点 / 多点交叉生成子代​

1. 变异：随机改变基因（小概率事件）

代码示例（包含可视化）

import numpy as np
import matplotlib.pyplot as plt
import random

def genetic_algorithm(func, dim=2, pop_size=100, max_gen=200, mut_rate=0.1, elite_ratio=0.1):
    # 初始化种群
    population = np.random.uniform(-5, 5, (pop_size, dim))
    best_fitness_history = []  # 记录每代最优适应度

    for gen in range(max_gen):
        # 计算适应度（Sphere函数值越小越好）
        fitness = func(population)
        best_fitness = np.min(fitness)
        best_fitness_history.append(best_fitness)

        # 选择（适应度标准化为正值）
        max_fitness = np.max(fitness)
        scaled_fitness = max_fitness - fitness + 1e-6  # 防止除以零
        prob = scaled_fitness / scaled_fitness.sum()
        selected_idx = np.random.choice(pop_size, pop_size, p=prob)
        selected = population[selected_idx]

        # 交叉（均匀交叉）
        children = []
        for i in range(0, pop_size, 2):
            p1 = selected[i]
            p2 = selected[i+1] if i+1 < pop_size else selected[0]
            mask = np.random.rand(dim) < 0.5
            child1 = np.where(mask, p1, p2)
            child2 = np.where(mask, p2, p1)
            children.extend([child1, child2])

        # 变异（非均匀变异）
        children = np.array(children)
        mutate_mask = np.random.rand(*children.shape) < mut_rate
        mutation = np.random.normal(0, 0.5*(1-gen/max_gen), children.shape)  # 变异幅度递减
        children = np.where(mutate_mask, children + mutation, children)

        # 精英保留：保留前10%的最优个体
        elite_num = int(pop_size * elite_ratio)
        elite_idx = np.argsort(fitness)[:elite_num]
        population = np.vstack([population[elite_idx], children[:pop_size - elite_num]])

        # 可视化更新（每20代绘制一次）
        if gen % 20 == 0 or gen == max_gen-1:
            plt.clf()
            # 适应度曲线
            plt.subplot(1, 2, 1)
            plt.plot(best_fitness_history, 'r-')
            plt.title(f'Generation {gen}, Best Fitness: {best_fitness:.4f}')
            plt.xlabel('Generation')
            plt.ylabel('Best Fitness')
            # 种群分布散点图
            plt.subplot(1, 2, 2)
            plt.scatter(population[:, 0], population[:, 1], c='b', alpha=0.5)
            plt.xlim(-5, 5)
            plt.ylim(-5, 5)
            plt.title('Population Distribution')
            plt.pause(0.1)
    
    plt.show()
    return population[np.argmin(func(population))]

# 目标函数：Sphere函数
best_solution = genetic_algorithm(lambda x: np.sum(x**2, axis=1), dim=2)
print("最优解:", best_solution)  # 应接近[0, 0]

2. 模拟退火算法（Simulated Annealing）

模拟退火算法基于固体退火原理，通过随机扰动和 Metropolis 准则跳出局部最优。关键参数包括初始温度、降温策略和终止温度。

代码示例

import math
import random
import numpy as np
import matplotlib.pyplot as plt

def simulated_annealing(func, x0, T0=100, Tf=1e-8, alpha=0.99, max_iter=1000):
    # 转换初始点为numpy数组
    x = np.array(x0, dtype=np.float64)
    best_x = x.copy()
    best_f = func(x)
    
    # 记录历史数据用于可视化
    history = {'temp': [], 'best_f': [], 'current_f': [], 'x': []}
    
    T = T0
    for i in range(max_iter):
        # 生成新解（使用numpy数组运算）
        x_new = x + T * np.random.uniform(-1, 1, size=x.shape)
        f_new = func(x_new)
        f_current = func(x)
        
        # Metropolis准则
        if f_new < f_current or random.random() < math.exp((f_current - f_new)/T):
            x = x_new
            if f_new < best_f:
                best_x = x_new.copy()
                best_f = f_new
        
        # 降温
        T *= alpha
        
        # 记录数据
        history['temp'].append(T)
        history['best_f'].append(best_f)
        history['current_f'].append(f_current)
        history['x'].append(x.copy())
        
        # 终止条件
        if T < Tf:
            break
            
        # 动态可视化（每100代更新一次）
        if i % 100 == 0 or i == max_iter-1:
            plt.clf()
            
            # 温度曲线
            plt.subplot(2, 2, 1)
            plt.plot(history['temp'], 'r-')
            plt.title('Temperature')
            plt.xlabel('Iteration')
            plt.ylabel('T')
            
            # 适应度曲线
            plt.subplot(2, 2, 2)
            plt.plot(history['best_f'], 'b-', label='Best')
            plt.plot(history['current_f'], 'g-', label='Current')
            plt.title('Fitness Value')
            plt.xlabel('Iteration')
            plt.ylabel('f(x)')
            plt.legend()
            
            # 解的变化轨迹
            plt.subplot(2, 2, 3)
            x_hist = np.array(history['x'])
            plt.plot(x_hist[:, 0], x_hist[:, 1], 'b-')
            plt.scatter(best_x[0], best_x[1], c='r', s=100)
            plt.title('Solution Path')
            plt.xlabel('x1')
            plt.ylabel('x2')
            
            # 当前解位置
            plt.subplot(2, 2, 4)
            plt.scatter(x[0], x[1], c='g', s=100)
            plt.xlim(min(x_hist[:,0])-0.5, max(x_hist[:,0])+0.5)
            plt.ylim(min(x_hist[:,1])-0.5, max(x_hist[:,1])+0.5)
            plt.title('Current Position')
            plt.xlabel('x1')
            plt.ylabel('x2')
            
            plt.tight_layout()
            plt.pause(0.1)
    
    plt.show()
    return best_x, best_f

# 目标函数：f(x, y) = x² + y²
def sphere_func(x):
    return x[0]**2 + x[1]**2

# 初始点
x0 = (2.0, 2.0)
best_x, best_f = simulated_annealing(sphere_func, x0)

print("最优解:", best_x)
print("最小值:", best_f)

3. 粒子群优化算法（Particle Swarm Optimization, PSO）

核心思想：模拟鸟群觅食，每个粒子根据 "个体最优" 和 "全局最优" 调整速度更新公式：​

​

​每个粒子根据自身历史最优位置（pbest）和全局最优位置（gbest）调整速度和位置。在实际应用粒子群优化算法时，粒子的数量、速度限制、学习因子等参数的设置对算法性能影响显著。例如，适当增加粒子数量能扩大搜索空间，但会增加计算复杂度；合适的学习因子可平衡全局搜索和局部开发能力。同时，为避免粒子陷入局部最优，可引入惯性权重动态调整策略，使算法在迭代初期注重全局搜索，后期聚焦局部优化。

代码示例

import numpy as np

def particle_swarm_optimization(func, dim, pop_size=30, max_iter=100):
    # 初始化粒子位置和速度
    particles = np.random.uniform(-5, 5, (pop_size, dim))
    velocities = np.zeros((pop_size, dim))
    pbest = particles.copy()
    pbest_fitness = np.array([func(x) for x in particles])
    gbest = pbest[np.argmin(pbest_fitness)]
    for _ in range(max_iter):
        for i in range(pop_size):
            # 更新速度和位置
            r1, r2 = np.random.rand(2)
            velocities[i] = 0.5 * velocities[i] + 2 * r1 * (pbest[i] - particles[i]) + 2 * r2 * (gbest - particles[i])
            particles[i] += velocities[i]
            # 边界处理
            particles[i] = np.clip(particles[i], -5, 5)
            # 更新pbest和gbest
            current_fitness = func(particles[i])
            if current_fitness < pbest_fitness[i]:
                pbest[i] = particles[i]
                pbest_fitness[i] = current_fitness
                if current_fitness < np.min(pbest_fitness):
                    gbest = pbest[np.argmin(pbest_fitness)]
    return gbest

# 目标函数：f(x, y) = x² + y²
func = lambda x: x[0]**2 + x[1]**2
gbest = particle_swarm_optimization(func, dim=2)
print("最优解:", gbest)

4. RMSProp 算法​

核心思想：对梯度平方进行指数加权平均，缓解 SGD 的震荡。在实际应用中，RMSProp算法常与学习率衰减策略结合使用，进一步增强算法的稳定性和收敛效率。同时，该算法在处理梯度稀疏问题时表现良好，能够有效适应不同参数的更新频率，在自然语言处理、时间序列预测等领域中得到广泛应用。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.colors as colors

class RMSPropOptimizer:
    """
    实现RMSProp优化算法，支持多种可视化功能
    """
    def __init__(self, objective_func, grad_func, lr=0.01, gamma=0.9, 
                 epsilon=1e-8, momentum=0.0, decay=0.0, lr_scheduler=None):
        """
        初始化RMSProp优化器
        
        参数:
            objective_func: 目标函数
            grad_func: 梯度计算函数
            lr: 学习率
            gamma: 梯度平方的移动平均衰减率
            epsilon: 防止除零的小常数
            momentum: 动量系数
            decay: 学习率衰减系数
            lr_scheduler: 学习率调度器函数
        """
        self.objective_func = objective_func
        self.grad_func = grad_func
        self.lr = lr
        self.gamma = gamma
        self.epsilon = epsilon
        self.momentum = momentum
        self.decay = decay
        self.lr_scheduler = lr_scheduler
        self.v = None  # 梯度平方的移动平均
        self.m = None  # 动量项
        self.history = {'params': [], 'loss': [], 'lr': []}
        
    def optimize(self, initial_params, max_iter=1000, tol=1e-6):
        """执行优化过程"""
        params = np.array(initial_params, dtype=np.float64)
        self.v = np.zeros_like(params)
        self.m = np.zeros_like(params)
        current_lr = self.lr
        
        for i in range(max_iter):
            # 记录当前参数和损失
            loss = self.objective_func(params)
            self.history['params'].append(params.copy())
            self.history['loss'].append(loss)
            self.history['lr'].append(current_lr)
            
            # 计算梯度
            grad = self.grad_func(params)
            
            # 更新梯度平方的移动平均
            self.v = self.gamma * self.v + (1 - self.gamma) * grad**2
            
            # 应用动量
            self.m = self.momentum * self.m + current_lr * grad / (np.sqrt(self.v) + self.epsilon)
            
            # 更新参数
            params -= self.m
            
            # 学习率衰减
            if self.decay > 0:
                current_lr = self.lr / (1 + self.decay * i)
            
            # 应用学习率调度器
            if self.lr_scheduler is not None:
                current_lr = self.lr_scheduler(i, current_lr)
            
            # 检查收敛
            if i > 0 and abs(self.history['loss'][-1] - self.history['loss'][-2]) < tol:
                break
                
        return params, self.history
    
    def visualize_optimization_path(self, x_range=(-5, 5), y_range=(-5, 5), 
                                    num_points=100, contour_levels=50, 
                                    title="RMSProp Optimization Path", 
                                    show=True, save_path=None):
        """可视化优化路径"""
        # 创建网格数据
        x = np.linspace(x_range[0], x_range[1], num_points)
        y = np.linspace(y_range[0], y_range[1], num_points)
        X, Y = np.meshgrid(x, y)
        Z = np.zeros_like(X)
        
        # 计算网格上的函数值
        for i in range(num_points):
            for j in range(num_points):
                Z[i, j] = self.objective_func([X[i, j], Y[i, j]])
        
        # 创建图形
        fig, ax = plt.subplots(figsize=(10, 8))
        contour = ax.contourf(X, Y, Z, levels=contour_levels, cmap='viridis', alpha=0.8)
        cbar = fig.colorbar(contour, ax=ax)
        cbar.set_label('Function Value')
        
        # 绘制优化路径
        params_history = np.array(self.history['params'])
        ax.plot(params_history[:, 0], params_history[:, 1], 'r-o', markersize=4, linewidth=1.5)
        
        # 绘制起点和终点
        ax.plot(params_history[0, 0], params_history[0, 1], 'bo', markersize=8, label='Start')
        ax.plot(params_history[-1, 0], params_history[-1, 1], 'go', markersize=8, label='End')
        
        # 设置图形属性
        ax.set_xlabel('Parameter 1')
        ax.set_ylabel('Parameter 2')
        ax.set_title(title)
        ax.legend()
        ax.grid(True, linestyle='--', alpha=0.7)
        
        if save_path:
            plt.savefig(save_path, dpi=300, bbox_inches='tight')
        if show:
            plt.show()
        
        return fig, ax
    
    def visualize_loss_curve(self, title="RMSProp Loss Curve", show=True, save_path=None):
        """可视化损失曲线"""
        fig, ax = plt.subplots(figsize=(10, 6))
        ax.plot(self.history['loss'], 'b-', linewidth=2)
        ax.set_xlabel('Iteration')
        ax.set_ylabel('Loss')
        ax.set_title(title)
        ax.grid(True, linestyle='--', alpha=0.7)
        
        # 添加对数刻度
        ax.set_yscale('log')
        
        if save_path:
            plt.savefig(save_path, dpi=300, bbox_inches='tight')
        if show:
            plt.show()
        
        return fig, ax
    
    def visualize_learning_rate(self, title="Learning Rate Schedule", show=True, save_path=None):
        """可视化学习率变化"""
        fig, ax = plt.subplots(figsize=(10, 6))
        ax.plot(self.history['lr'], 'g-', linewidth=2)
        ax.set_xlabel('Iteration')
        ax.set_ylabel('Learning Rate')
        ax.set_title(title)
        ax.grid(True, linestyle='--', alpha=0.7)
        
        if save_path:
            plt.savefig(save_path, dpi=300, bbox_inches='tight')
        if show:
            plt.show()
        
        return fig, ax
    
    def create_animation(self, x_range=(-5, 5), y_range=(-5, 5), num_points=100, 
                         contour_levels=50, title="RMSProp Optimization Animation", 
                         fps=10, save_path=None):
        """创建优化过程动画"""
        # 创建网格数据
        x = np.linspace(x_range[0], x_range[1], num_points)
        y = np.linspace(y_range[0], y_range[1], num_points)
        X, Y = np.meshgrid(x, y)
        Z = np.zeros_like(X)
        
        # 计算网格上的函数值
        for i in range(num_points):
            for j in range(num_points):
                Z[i, j] = self.objective_func([X[i, j], Y[i, j]])
        
        # 创建图形
        fig, ax = plt.subplots(figsize=(10, 8))
        contour = ax.contourf(X, Y, Z, levels=contour_levels, cmap='viridis', alpha=0.8)
        cbar = fig.colorbar(contour, ax=ax)
        cbar.set_label('Function Value')
        
        # 初始化路径线和当前点
        path_line, = ax.plot([], [], 'r-', linewidth=1.5)
        current_point, = ax.plot([], [], 'ro', markersize=8)
        
        # 绘制起点
        params_history = np.array(self.history['params'])
        ax.plot(params_history[0, 0], params_history[0, 1], 'bo', markersize=8, label='Start')
        
        # 设置图形属性
        ax.set_xlabel('Parameter 1')
        ax.set_ylabel('Parameter 2')
        ax.set_title(title)
        ax.grid(True, linestyle='--', alpha=0.7)
        ax.legend()
        
        def init():
            path_line.set_data([], [])
            current_point.set_data([], [])
            return path_line, current_point
        
        def update(frame):
            if frame > len(params_history):
                frame = len(params_history)
            path_line.set_data(params_history[:frame, 0], params_history[:frame, 1])
            current_point.set_data(params_history[frame-1, 0], params_history[frame-1, 1])
            return path_line, current_point
        
        # 创建动画
        ani = FuncAnimation(fig, update, frames=len(params_history)+10, 
                            init_func=init, blit=True, interval=1000/fps)
        
        if save_path:
            ani.save(save_path, writer='ffmpeg', fps=fps)
        
        plt.close(fig)
        return ani
    
    def visualize_3d(self, x_range=(-5, 5), y_range=(-5, 5), num_points=100, 
                    title="RMSProp 3D Visualization", show=True, save_path=None):
        """创建3D可视化"""
        # 创建网格数据
        x = np.linspace(x_range[0], x_range[1], num_points)
        y = np.linspace(y_range[0], y_range[1], num_points)
        X, Y = np.meshgrid(x, y)
        Z = np.zeros_like(X)
        
        # 计算网格上的函数值
        for i in range(num_points):
            for j in range(num_points):
                Z[i, j] = self.objective_func([X[i, j], Y[i, j]])
        
        # 创建3D图形
        fig = plt.figure(figsize=(12, 10))
        ax = fig.add_subplot(111, projection='3d')
        
        # 绘制表面
        surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8, 
                              linewidth=0, antialiased=True)
        
        # 添加颜色条
        fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)
        
        # 绘制优化路径
        params_history = np.array(self.history['params'])
        loss_history = np.array(self.history['loss'])
        ax.plot(params_history[:, 0], params_history[:, 1], loss_history, 'r-o', markersize=4, linewidth=1.5)
        
        # 绘制起点和终点
        ax.plot([params_history[0, 0]], [params_history[0, 1]], [loss_history[0]], 
                'bo', markersize=8, label='Start')
        ax.plot([params_history[-1, 0]], [params_history[-1, 1]], [loss_history[-1]], 
                'go', markersize=8, label='End')
        
        # 设置图形属性
        ax.set_xlabel('Parameter 1')
        ax.set_ylabel('Parameter 2')
        ax.set_zlabel('Loss')
        ax.set_title(title)
        ax.legend()
        
        if save_path:
            plt.savefig(save_path, dpi=300, bbox_inches='tight')
        if show:
            plt.show()
        
        return fig, ax

# 示例：优化Rastrigin函数
def rastrigin_function(params, A=10):
    """Rastrigin测试函数"""
    x, y = params
    return A * 2 + (x**2 - A * np.cos(2 * np.pi * x)) + (y**2 - A * np.cos(2 * np.pi * y))

def rastrigin_gradient(params, A=10):
    """Rastrigin函数的梯度"""
    x, y = params
    grad_x = 2 * x + 2 * A * np.pi * np.sin(2 * np.pi * x)
    grad_y = 2 * y + 2 * A * np.pi * np.sin(2 * np.pi * y)
    return np.array([grad_x, grad_y])

# 学习率调度器
def learning_rate_scheduler(epoch, lr):
    """余弦退火学习率调度器"""
    T_max = 100
    eta_min = 0.0001
    return eta_min + (lr - eta_min) * (1 + np.cos(np.pi * epoch / T_max)) / 2

# 主函数：演示RMSProp优化过程
def main():
    # 初始化优化器
    optimizer = RMSPropOptimizer(
        objective_func=rastrigin_function,
        grad_func=rastrigin_gradient,
        lr=0.1,
        gamma=0.9,
        momentum=0.5,
        decay=0.01,
        lr_scheduler=learning_rate_scheduler
    )
    
    # 执行优化
    initial_params = [-4, 4]
    optimal_params, history = optimizer.optimize(
        initial_params=initial_params,
        max_iter=100,
        tol=1e-6
    )
    
    print(f"优化结果: {optimal_params}")
    print(f"最终损失: {history['loss'][-1]}")
    
    # 可视化
    optimizer.visualize_optimization_path(
        x_range=(-5, 5), 
        y_range=(-5, 5),
        title="RMSProp Optimization Path on Rastrigin Function"
    )
    
    optimizer.visualize_loss_curve(
        title="RMSProp Loss Curve"
    )
    
    optimizer.visualize_learning_rate(
        title="RMSProp Learning Rate Schedule"
    )
    
    optimizer.visualize_3d(
        x_range=(-5, 5),
        y_range=(-5, 5),
        title="RMSProp 3D Optimization Visualization"
    )
    
    # 创建动画（取消注释以生成动画）
    # ani = optimizer.create_animation(
    #     x_range=(-5, 5),
    #     y_range=(-5, 5),
    #     title="RMSProp Optimization Animation",
    #     save_path="rmsprop_animation.gif"
    # )

if __name__ == "__main__":
    main()

五、自适应学习率优化算法

1. Adam 优化器（深度学习首选）

Adam 结合动量法和 RMSProp，通过计算梯度的一阶矩（均值）和二阶矩（方差）自适应调整学习率。其更新公式为：
 

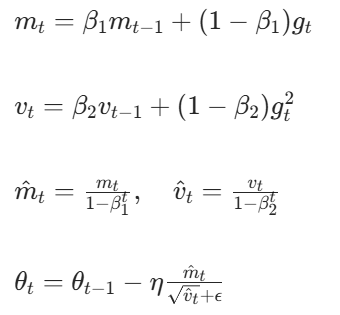
核心机制：​

• 一阶矩（动量）：指数加权平均梯度​

• 二阶矩（RMSProp）：指数加权平均梯度平方​

• 偏差修正：初始阶段校正偏差

代码示例

import numpy as np

def adam_optimizer(grad_func, x0, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8, max_iter=1000):
    x = x0
    m = np.zeros_like(x)
    v = np.zeros_like(x)
    for t in range(1, max_iter+1):
        g = grad_func(x)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g ** 2)
        m_hat = m / (1 - beta1 ** t)
        v_hat = v / (1 - beta2 ** t)
        x -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
    return x

# 目标函数：f(x) = x²
grad_func = lambda x: 2 * x
x0 = 5.0
x_opt = adam_optimizer(grad_func, x0)
print("最优解:", x_opt)

2. Adagrad 算法

Adagrad 根据历史梯度的平方和调整学习率，公式为：
 

代码示例

import numpy as np

def adagrad_optimizer(grad_func, x0, learning_rate=0.01, epsilon=1e-8, max_iter=1000):
    x = x0
    r = np.zeros_like(x)
    for _ in range(max_iter):
        g = grad_func(x)
        r += g ** 2
        x -= learning_rate * g / (np.sqrt(r) + epsilon)
    return x

# 目标函数：f(x) = x²
grad_func = lambda x: 2 * x
x0 = 5.0
x_opt = adagrad_optimizer(grad_func, x0)
print("最优解:", x_opt)

六、总结与展望

本文系统梳理了梯度下降、牛顿法、遗传算法、模拟退火、粒子群优化、Adam、Adagrad 等常见最优化方法，涵盖原理、代码实现和适用场景。传统方法（如梯度下降、牛顿法）理论成熟但易陷入局部最优，智能算法（如遗传算法、模拟退火）鲁棒性强但计算复杂度高，自适应学习率算法（如 Adam、Adagrad）在深度学习中表现优异。

最优化方法对比与选择指南

方法	收敛速度	全局最优	计算复杂度	适用场景
梯度下降	慢	局部最优	O(n)	大规模数据（MBGD）
牛顿法	极快	局部最优	O(n³)	小规模无约束问题
遗传算法	中等	全局搜索	O(pop*dim)	离散 / 复杂目标函数
Adam	快	局部最优	O(n)	深度学习（默认选择）
SMO	中等	全局最优	O(m²n)	凸二次规划（SVM 训练）

本文覆盖了最优化领域的核心方法：​

1. 数学优化：梯度下降（BGD/SGD/MBGD）、牛顿法、拉格朗日乘数法​

1. 约束处理：KKT 条件、SMO 算法​

1. 智能算法：遗传算法、粒子群优化​

1. 自适应优化：Adam、RMSProp​

实际应用中需根据问题特性选择：​

• 连续可导问题：优先梯度下降 / Adam（深度学习）、牛顿法（小规模）​

• 离散 / 多峰问题：尝试遗传算法 / PSO（需调参）​

• 凸优化问题：利用 KKT 条件求解解析解​

未来方向包括：​

• 结合深度学习的元优化（Hyperopt）​

• 分布式优化（大规模数据并行处理）​

• 量子计算优化（解决 NP 难问题）

七、参考文献

1. 孙文瑜，徐成贤，朱德通。最优化方法（第二版）[M]. 高等教育出版社，2004.
2. 袁亚湘，孙文瑜。最优化理论与方法 [M]. 科学出版社，1997.
3. Diederik P. Kingma, Jimmy Ba. Adam: A Method for Stochastic Optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
4. Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011, 12(Jul):2121-2159.
5. Eberhart R C, Kennedy J. A new optimizer using particle swarm theory[C]//Micro Machine and Human Science, 1995. MHS'95. Proceedings of the Sixth International Symposium on. IEEE, 1995: 39-43.
6. Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing[J]. science, 1983, 220(4598): 671-680.
7. 《最优化方法》（孙文瑜，高等教育出版社，2004）​
8. 《Deep Learning》（Goodfellow, Bengio, Courville, 2016）​
9. 李航《统计学习方法》（第二版，清华大学出版社，2019）​
10. Goldberg D E. 《Genetic Algorithms in Search, Optimization, and Machine Learning》(1989)​
11. Kingma D P, Ba J. Adam: A Method for Stochastic Optimization (arXiv:1412.6980, 2014)

 

注意：代码需根据具体问题调整参数和边界条件，建议结合数据特性选择合适的优化方法。