RNN

---

前言

\qquad 在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种最基本的网络所有输入之间是没有联系的，只能单独的处理每一个输入进行预测。但如果我们要对时间序列这种类似的数据进行结果预测，也就是这种的前因和后果都是有联系的数据，传统神经网络就不行了，比如对于天空很____",这里填空，我们根据上文可以推断出来大概率是填“蓝“，但普通神经网络要做到这一步就相当得难了，因为一个句子中前后单词并不是独立的。所以我们引进了RNN来解决这个问题。

---

循环神经网络（Recurrent Neural Network, RNN）

\qquad 循环神经网络是用来处理序列数据的神经网络。
\qquad 时间序列数据（time series data）是在不同时间上收集到的数据，用于所描述现象随时间变化的情况。（From 百度百科）序列数据也可以不是时间，比如文字序列，但序列数据有一个特点——后面的数据跟前面的数据有关系。

RNN结构

\qquad 循环神经网络t时刻的的状态与t-1时刻的状态和t时刻的输入有关。RNN会记忆之前的信息，并利用之前的信息影响后面节点的输出。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。
# 正向传播
上图展示了一个典型的循环神经网络。在每一时刻t,循环神经网络会针对该时刻的输入结合当前模型的状态给出一个输出，并更新模型状态。从图中可以看到，循环神经网络的主体结构A的输入除了来自输入层x_t,还有一个循环的边来提供上一时刻的隐藏状态 h_t-1。 在每一个时刻，循环神经网络的模块A在读取了x_t和h_t-1之后,会生成新的隐藏状态h_t,并产生本时刻的输出O_t。由于模块A中的运算和变量在不同时刻是相同的(参数共享)，因此循环神经网络理论上可以被看作是同一神经网络结构被无限复制的结果。

将完整的输入输出序列展开，可以得到下图所展示的结构。在图中可以更加清楚地看到循环神经网络在每一个时刻会有个输入 x_t,然后根据循环神经网络前一时刻的状态S_t-1计算新的状态S_t,并输出O_t。

对于t时刻：
$$S_t=f(W\times S_{t-1}+U\times x_t)（1）$$
$$O_t=g(V\times S_t)（2）$$

\qquad 式（1）中，W是隐藏层节点到隐藏层节点的权重矩阵，S_t-1为t-1时刻的状态，x_t是t时刻每个输入单元的值，f是一个激活函数，S_t为t时刻的状态。式（2）中，V是输出层的权重矩阵，g是激活函数。
如果反复把式（1）带入到式（2），我们将得到：

循环神经网络当前的状态_t, 是根据上一时刻的状态h-t和当前的输入x共同决定的。在时刻t状态S_t-1浓缩了前面序列x₀，x₁, … x_t-1的信息，用于作为输出O_t的参考。由于序列的长度可以无限延长，维度有限的h状态不可能将序列的全部信息都保存下来，因此模型必须学习只保留与后面任务O_t O_t+1…相关的最重要的信息。

RNN正向传播计算举例

假设状态的维度为2，输入、输出的维度都为1，循环体中的全连接层中权重为：
$$w_{rnn}=\left[\begin{array}{cc}0.1& 0.2\\ 0.3& 0.4\\ 0.5& 0.6\end{array}\right]$$
偏置项的大小为b_rnn=[0.1,-0.1]，用于输出的全连接层权重为：
$$w_{rnn}=\left[\begin{array}{c}1.0\\ 2.0\end{array}\right]$$
偏置项大小为b_output=0.1。在t₀时刻，将状态初始化为h_init=[0,0]，当前输入为1，拼接得到的向量为[0,0,1],通过循环体中的全连接层神经网络得到的结果为：
$$tanh([0,0,1]\times \left[\begin{array}{cc}0.1& 0.2\\ 0.3& 0.4\\ 0.5& 0.6\end{array}\right]+[0.1,-0.1])=tanh([0.6,0.5])=[0.537,0.462]$$
将该向量作为输入提供给用于输出得全连接神经网络可以得到t₀时刻得得最终输出：
$$[0.537,0.462]\times \left[\begin{array}{c}1.0\\ 2.0\end{array}\right]+0.1=1.56$$
[0.537,0.462]作为t₁时刻的输入状态，以及样本输入2，输入到与t₀时刻相同的网络结构中，即与t₀时刻相同权重进行运算，可推导得出t₁时刻的状态为[0.860，0，884]，t₁时刻的输出为2.73。

反向传播(Back-Propagation Through Time,BPTT)

\qquad RNN神经网络利用反向传播方法将输出层的误差加和，然后对各个权重的参数矩阵求梯度$\nabla$U,$\nabla$V,$\nabla$w，再利用梯度下降法更新各个权重。
\qquad 循环神经网络每一时刻都有一个输出，对于每一时刻t的RNN网络，网络的输出O_t会产生一定误差e_t误差的损失函数， 可以是交叉嫡也可以是平方误差等等。那么RNN的总损失为所有时刻（或部分时刻）上的损失函数的总和。总的误差为E=$\sum$e_t。

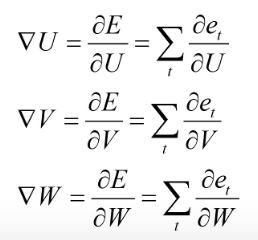
\qquad 对于输出O_t =g(VS_t),对于任意损失函数，求取V将是简单的，可以直接求取每个时刻的$\partial$e_t / $\partial$v，由于它不存在和之前的状态依赖,可以直接求导取得，然后简单求和即可。
L为损失函数。
$$O_t=g(V\times S_t)（2）$$
对于t时刻：

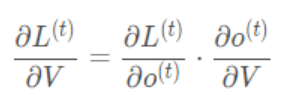
RNN的损失也是会随着时间累加的，所以不能只求t时刻的偏导。

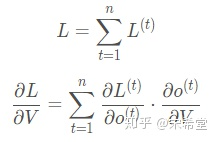
$对w求梯度：$

$S_t=f(W\times S_{t-1}+U\times x_t)$
$O_t=g(V\times S_t)$

$S_3=f(W{S}_2+U{x}_3)$与S₂有关,S₂又与S₁和W有关, 如此反复. 所以如果我们想求W的导数，我们不能仅把S₂当做常数。我们需要考虑每一时间步的梯度。换句话说，因为RNN中参数共享，W在每一步都被使用直到最后的输出，所以我们需要从t=3开始后向传播梯度直到t=0。对于$\nabla$W,$\nabla$U的计算不能直接求导，因此需要用链式求导法则。
t时刻 W的梯度：
$$\frac{\partial L_t}{\partial W}=\frac{\partial L_t}{\partial W^0}+\frac{\partial L_t}{\partial W^1}+\cdots +\frac{\partial L_t}{\partial W^t}$$
$$\frac{\partial L_t}{\partial W}=\sum _{i=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}\frac{\partial S_t}{\partial S_i}\frac{\partial S_i}{\partial W}$$
$$这里\frac{\partial L_t}{\partial O_t}、\frac{\partial O_t}{\partial S_t}、\frac{\partial S_i}{\partial W}都比较容易求得$$
\qquad 在RNN反向传播过程中，某一序列位置的梯度损失由当前时刻t的输出对应的梯度损失和下一时刻t+1梯度损失共同决定。
$$\frac{\partial L_t}{\partial S_t}=\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}+\frac{\partial L_{t+1}}{\partial S_{t+1}}\frac{\partial S_{t+1}}{\partial h_t}$$
$$其中，\frac{\partial S_t}{\partial S_i}=\frac{\partial S_t}{\partial S_{t-1}}\frac{\partial S_{t-1}}{\partial S_{t-2}}\cdots \frac{\partial S_{i+1}}{\partial S_i}=\prod _{k=i}^{t-1}\frac{\partial S_{k+1}}{\partial S_k}$$
$$S_t=f(U\times x_t+W\times S_{t-1})$$
$$\frac{\partial S_{k+1}}{\partial S_k}=f\prime \times W$$

假设只有三个时刻，那么在第三个时刻 L对W的偏导数为：

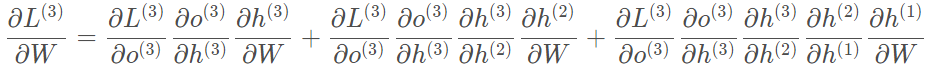
整体的偏导公式就是将其按时刻再一一加起来。
$对U求梯度：$

t时刻 U的梯度：
$$\frac{\partial L_t}{\partial U}=\frac{\partial L_t}{\partial U^0}+\frac{\partial L_t}{\partial U^1}+\cdots +\frac{\partial L_t}{\partial U^t}$$
$$\frac{\partial L_t}{\partial U}=\sum _{i=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}\frac{\partial S_t}{\partial S_i}\frac{\partial S_i}{\partial U}$$
$$这里\frac{\partial L_t}{\partial O_t}、\frac{\partial O_t}{\partial S_t}、\frac{\partial S_i}{\partial U}都比较容易求得$$
$$其中，\frac{\partial S_t}{\partial S_i}=\frac{\partial S_t}{\partial S_{t-1}}\frac{\partial S_{t-1}}{\partial S_{t-2}}\cdots \frac{\partial S_{i+1}}{\partial S_i}=\prod _{k=i}^{t-1}\frac{\partial S_{k+1}}{\partial S_k}$$
$$S_t=f(U\times x_t+W\times S_{t-1})$$
$$\frac{\partial S_{k+1}}{\partial S_k}=f\prime \times W$$
假设只有三个时刻，那么在第三个时刻 L对U的偏导数为：

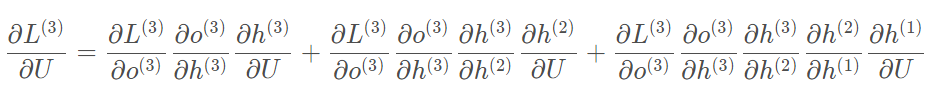
整体的偏导公式就是将其按时刻再一一加起来。

RNN 的变体及应用

N VS 1

这种结构通常用来处理序列分类问题，输入是一个序列，输出是一个单独的值而不是序列。
应用：情感分类：如输入一段文字判别它所属的类别，输入一个句子判断其情感倾向，输入一段视频并判断它的类别。举例：“天气真好”。

1 VS N

输入不是序列而输出为序列。
应用：图像描述：输入为一张图片，输出是对这张图片的描述信息。图像生成文字。

N VS M

N vs M这种结构又叫Encoder-Decoder模型，也可以称之为Seq2Seq模型。

Encoder-Decoder结构先将输入数据编码成一个上下文向量c，得到c之后，就用另一个RNN网络对其进行解码，这部分RNN网络被称为Decoder。具体做法就是将c当做之前的初始状态h₀输入到Decoder中.
应用：机器翻译：输入为源语言中的一个序列数据（比如：中文），输出是目标语言序列数据（比如：英语），比如谷歌翻译、有道翻译等。

RNN的不足

梯度爆炸

$$\frac{\partial S_{k+1}}{\partial S_k}=f\prime \times W$$
如果参数 W的值太大，随着序列长度同样存在长期依赖的情况，梯度呈指数级增长，最后到输入时，梯度将会非常大，我们会得到一个非常大的权重更新，那么产生问题就是梯度爆炸。

梯度消失

RNN存在梯度消失的问题，就会遗忘掉前面的信息。比如，“今天北方有沙尘暴，伴随大风…天空都是_____”

$h_t=f(W\times h_{t-1}+U\times x_t)$

sigmoid图和导数图：

tanh图及其导数图：

\qquad sigmoid和tanh都把输出压缩在了一个范围之内。他们的导数图像也非常相近，我们可以从中观察到，sigmoid函数的导数范围是(0,0.25]，tanh函数的导数范围是(0,1]，他们的导数最大都不大于1，大部分都是小于1的数在做累乘。假设有10个时刻，依次求导再连乘，连续乘一个小于1的数字，会导致梯度趋近于0，最终导致梯度消失。梯度消失就意味消失那一层的参数再也不更新，那么那一层隐层就变成了单纯的映射层，毫无意义了，对较长的时间，或者较长的string，很多时候前面的数据对后面的数据影响就很小甚至没影响了。
\qquad 长短期记忆网络（Long Short-Term Memory，LSTM）就很好的弥补了RNN梯度消失的不足，LSTM增加了遗忘门，更有效地决定哪些信息被忘掉，哪些信息被保留。

参考：https://zhuanlan.zhihu.com/p/112998607
https://blog.csdn.net/zhaojc1995/article/details/80572098