《算法导论》-分治策略，矩阵相乘Strassen算法(伪代码,Java)

一.矩阵基础

     因为计算机相关专业都学了线性代数基础的知识这里就不介绍了，首先来看一下这个矩阵：

 A，B矩阵相乘得到C矩阵：

 如果要计算上述矩阵，最简单的通用方法是通过三个循环也就是复杂度为O(n^3)

因为笔者常用java所以简单的用java来表示:

package Main;
public class Test {
    public static void main(String[] args) {
        int[][] A = {{1,2},{2,1}};
        int[][] B = {{1,2},{3,4}};
        int[][] C = new int[2][2];  //anser
        for(int i=0;i<A.length;i++){
            for(int j=0;j<B.length;j++){
                for(int k=0;k<C.length;k++){
                    C[i][j] += A[i][k] * B[k][j];
                }
            }
        }
        for(int i=0;i<A.length;i++){
            for(int j=0;j<B.length;j++) {
                System.out.print(C[i][j]+" ");
            }
            System.out.println();
        }
    }
}

二.矩阵公式与递归

 通过上述循环的方法我们发现计算无非用到了下面几个公式：

两个n*n的矩阵相乘要用到2个n/2*n/2的矩阵相乘，8次乘法，4次加法每次乘法加法的公式是相同的所以可以利用上述公式进行递归运算得到计算结果：

SQUARE-MATRIX-MULTIPLY(A,B)
n = A.rows
let C be a new n*n matrix
if n==1
   c11 = a11 * b11
else
   C11 = SQUARE-MATRIX-MULTIPLY(A11,B11)+
         SQUARE-MATRIX-MULTIPLY(A12,B21)
   C12 = SQUARE-MATRIX-MULTIPLY(A11,B12)+
         SQUARE-MATRIX-MULTIPLY(A12,B22)
   C21 = SQUARE-MATRIX-MULTIPLY(A21,B11)+
         SQUARE-MATRIX-MULTIPLY(A22,B21)
   C22 = SQUARE-MATRIX-MULTIPLY(A21,B12)+
         SQUARE-MATRIX-MULTIPLY(A22,B22)
return c

再来看看多阶矩阵，其实与2*2的矩阵是一样的，一个大矩阵可以化为几个小矩阵：

 

三.Strassen算法思想

上述递归过程也并没有减少乘与加的次数，Strassen提供了新的方法：

还是这个矩阵：

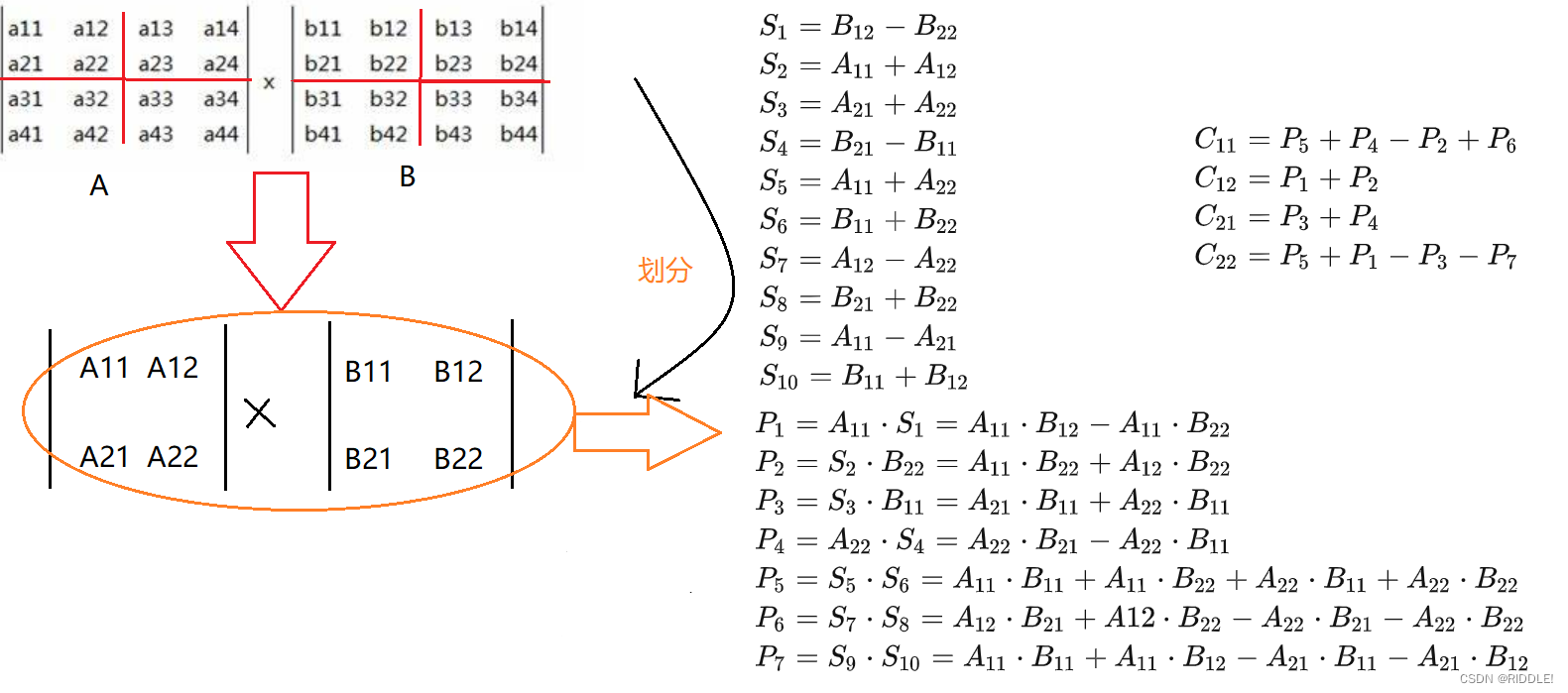
对其进行分解：

 创建10个n/2小矩阵，递归计算7个矩阵

通过这七个P矩阵计算C矩阵：

计算C的结果并不复杂，计算方式如下（以C12为例）：

 共计7次乘法，6次加法，4次减法，时间复杂度：

Strassen算法的特点是适用于比较大的矩阵，通过递归划分，再用上述公式解决。至于公式是怎么来的：这是Strassen做了很多努力得来的。总结：

四.伪代码实现

n为偶数时毋庸置疑Strassen算法成立，在这里考虑到奇数情况，这种情况不能使用Strassen算法，将n*n矩阵分解为(n-1)*(n-1)与一个(n-1)*1

NAIVE-MULTIPLY(A,B) //普通算法
  m = A.rows
  n = B.columns
  p = A.columns
  for i = 1 to m
    for j = 1 to n
      cij = 0
       for k = 1 to p
         cij += aik * bkj

STRASSEN-SQUARE-MATRIX-MULTIPLY(A,B)
n = A.rows
if n == 1
  c11 = a11+b11
else if n is odd   //为奇数情况
  divide An*n into 4sub-matrices A11(n-1)*(n-1),A12(n-1)*1,A21(n-1)*1,A21_1*1 //分为小矩阵
  divide Bn*n into 4sub-matrices B11(n-1)*(n-1),B12(n-1)*1,B21(n-1)*1,B21_1*1
  divide Cn*n into 4sub-matrices C11(n-1)*(n-1),C12(n-1)*1,C21(n-1)*1,C21_1*1
  C11 = STRASSEN-SQUARE-MATRIX-MULTIPLY(A11,B11) + NAIVE-MULTIPLY(A12,B21)
  C12 = NAIVE-MULTIPLY(A11,B12) + NAIVE-MULTIPLY(A12,B22)
  C21 = NAIVE-MULTIPLY(A21,B11) + NAIVE-MULTIPLY(A22,B21)
  C22 = NAIVE-MULTIPLY(A21,B12) + NAIVE-MULTIPLY(A22,B22)
else
  divide An*n into 4sub-matrices A11(n/2)*(n/2),A12(n/2)*(n/2),A21(n/2)*(n/2),A21(n/2)*(n/2)    //分为小矩阵
  divide Bn*n into 4sub-matrices B11(n/2)*(n/2),B12(n/2)*(n/2),B21(n/2)*(n/2),B21(n/2)*(n/2)
  divide Cn*n into 4sub-matrices C11(n/2)*(n/2),C12(n/2)*(n/2),C21(n/2)*(n/2),C21(n/2)*(n/2)
  S1 = B12 - B22
  S2 = A11 - A12
  S3 = A21 + A22
  S4 = B21 - B11
  S5 = A11 + A22
  S6 = B11 + B22
  S7 = A12 - A22
  S8 = B21 + B22
  S9 = A11 - A21
  S10 = B11 + B12
  P1 = STRASSEN-SQUARE-MATRIX-MULTIPLY(A11,S1)
  P2 = STRASSEN-SQUARE-MATRIX-MULTIPLY(S2,B22)
  P3 = STRASSEN-SQUARE-MATRIX-MULTIPLY(S3,B11)
  P4 = STRASSEN-SQUARE-MATRIX-MULTIPLY(A22,S4)
  P5 = STRASSEN-SQUARE-MATRIX-MULTIPLY(S5,S6)
  P6 = STRASSEN-SQUARE-MATRIX-MULTIPLY(S7,S8)
  P7 = STRASSEN-SQUARE-MATRIX-MULTIPLY(S9,S10)
  C11 = P5 + P4 - P2 + P6
  C12 = P1 + P2
  C21 = P3 + P4
  C22 = P5 + P1 - P3 -P7
return C 

五.Java实现

package Main;

/****************
 * @author RIDDLE!
 * @data  2022/11/24
 ****************/
public class Test {
    public static void main(String[] args) {
        int[][] A = {{1,2,1,2},
                     {2,1,2,1},
                     {1,2,2,1},
                     {1,2,2,1}};
        int[][] B = {{1,2,1,2},
                     {3,4,3,4},
                     {1,5,6,7},
                     {2,3,4,6}};
        int[][] C = new int[4][4];
        Strassen(A,B,C);
        Show(C);
    }

    public static void Show(int[][] C){
        for(int i=0;i<C.length;i++){
            for(int j=0;j<C.length;j++) {
                System.out.print(C[i][j]+" ");
            }
            System.out.println();
        }
    }
    public static void Strassen(int[][] A,int[][] B,int[][] C){
        int temp1[][] = new int[A.length/2][A.length/2];
        int temp2[][] = new int[A.length/2][A.length/2];

        int[][] P1 = new int[A.length/2][A.length/2];
        int[][] P2 = new int[A.length/2][A.length/2];
        int[][] P3 = new int[A.length/2][A.length/2];
        int[][] P4 = new int[A.length/2][A.length/2];
        int[][] P5 = new int[A.length/2][A.length/2];
        int[][] P6 = new int[A.length/2][A.length/2];
        int[][] P7 = new int[A.length/2][A.length/2];

        int[][] C11 = new int[A.length/2][A.length/2];
        int[][] C12 = new int[A.length/2][A.length/2];
        int[][] C21 = new int[A.length/2][A.length/2];
        int[][] C22 = new int[A.length/2][A.length/2];

        int[][] A11 = new int[A.length/2][A.length/2];
        int[][] A12 = new int[A.length/2][A.length/2];
        int[][] A21 = new int[A.length/2][A.length/2];
        int[][] A22 = new int[A.length/2][A.length/2];

        int[][] B11 = new int[B.length/2][B.length/2];
        int[][] B12 = new int[B.length/2][B.length/2];
        int[][] B21 = new int[B.length/2][B.length/2];
        int[][] B22 = new int[B.length/2][B.length/2];

        if(A.length == 1){
            matrixMul(A,B,C);
            return;
        }
        else{
            for (int i = 0; i < A.length / 2; i++) {
                for (int j = 0; j < A.length / 2; j++) {
                    A11[i][j] = A[i][j];
                    A12[i][j] = A[i][j + A.length / 2];
                    A21[i][j] = A[i + A.length / 2][j];
                    A22[i][j] = A[i + A.length / 2][j + A.length / 2];
                    B11[i][j] = B[i][j];
                    B12[i][j] = B[i][j + A.length / 2];
                    B21[i][j] = B[i + A.length / 2][j];
                    B22[i][j] = B[i + A.length / 2][j + A.length / 2];
                }
            }

            matrixSub(B12, B22, temp1);  //S1 = B12-B22
            Strassen(A11, temp1, P1);     //P1

            matrixSub(A11, A12, temp1);  //S2 = A11-A12
            Strassen(temp1, B22, P2);  //P2

            matrixSum(A21, A22, temp1);  //S3 = A21-A22
            Strassen(temp1, B11, P3);  //P3

            matrixSub(B21, B11, temp1);  //S4 = B21-B11
            Strassen(A22, temp1, P4);  //P4

            matrixSum(A11, A22, temp2);  //S5 = A11+A22
            matrixSum(B11, B22, temp1);  //S6 = B11+B22
            Strassen(temp2, temp1, P5);  //P5

            matrixSub(A12, A22, temp2);  //S7 = A12-A22
            matrixSum(B21, B22, temp1);  //S8 = B21+B22
            Strassen(temp2, temp1, P6);   //P6

            matrixSub(A11, A21, temp2);  //S9 = A11-A21
            matrixSum(B11, B12, temp1);  //S10 = B11+B12
            Strassen(temp2, temp1, P7); //P7


            matrixSum(P5, P4, temp2);//C11 = P5+P4-P2+P6
            matrixSub(temp2, P2, temp1);
            matrixSum(temp1, P6, C11);

            matrixSum(P1, P2, C12);//C12 = P1+P2

            matrixSum(P3, P4, C21);//C21 = P3+P4

            matrixSum(P5, P1, temp2);  // C22 = P5+P1-P3-P7
            matrixSub(temp2, P3, temp1);
            matrixSub(temp1, P7, C22);

            // 将C11,C12,C21,C22写入C中
            for (int i = 0; i < C.length / 2; i++) {
                for (int j = 0; j < C.length / 2; j++) {
                    C[i][j] = C11[i][j];
                    C[i][j + C.length / 2] = C12[i][j];
                    C[i + C.length / 2][j] = C21[i][j];
                    C[i + C.length / 2][j + C.length / 2] = C22[i][j];
                }
            }
        }

    }

    public static void matrixSum(int[][] A,int[][] B,int[][] temp1){  //矩阵加法
        for(int i=0;i<A.length;i++){
            for(int j=0;i<B.length;j++){
                temp1[i][j] = A[i][j] + B[i][j];
            }
        }
    }

    public static void matrixSub(int[][] A,int[][] B,int[][] temp2){  //矩阵减法
        for(int i=0;i< A.length;i++){
            for(int j=0;j< B.length;j++){
                temp2[i][j] = A[i][j] - B[i][j];
            }
        }
    }

    public static void matrixMul(int[][] A,int[][] B,int[][] temp){  //矩阵相乘
        for(int i=0;i<A.length;i++) {
            for (int j = 0; j < B.length; j++) {
                for (int k = 0; k < temp.length; k++) {
                    temp[i][j] += A[i][k] * B[k][j];
                }
            }
        }
    }

}