Elias Kiritsis《String Theory in a Nutshell》（埃利亚斯·基里西斯《简明弦论》）中文目录-CSDN博客

本文深入探讨了弦理论的历史、经典概念、量子化过程以及共形场论在理论中的核心作用。从点粒子过渡到弦，解释了振动模式和Virasoro约束。进一步阐述了玻色弦的量子行为、共形不变性、BRST量子化和共形代数。此外，详细介绍了超弦、D-膜、紧化技巧以及对偶关系在解决理论问题中的应用，如T-对偶和U-对偶。最后，讨论了黑洞熵、全息原理以及矩阵模型如何与弦论相互关联。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

几点说明：

① 我将 correspondence 直译为“对应”，而没有译作“对偶（duality）”。简而言之，correspondence 是 duality 的特殊情况，即一种特殊的对偶；

② 仅一处“膜”的英文为 membrane（文中已标出），其他均为 brane。brane 是 membrane 的派生词，专门用来描述弦论中的膜；

③ “锥形”指的是微分几何中的 conifold(锥流形)，它是一种推广的流形，而非 taper；

④ 物理和数学存在同词异译的情况，我这里基本采用物理上的译法，比如“非平庸（non-trivial）”而非“非平凡”、“算符（operator）”而非“算子”、“正规化（regularization）”而非“正则化”、“延拓（continuation）”而非“开拓”等。不过这里的 projective 是按数学的习惯译作“射影”，而非物理上的“投影”，原因在于更准确，简而言之，数学上通常默认“射影”指“中心投影”，而物理上通常默认“投影”为“平行投影”，同时在大陆地区一般用“射影”专门指代“正投影”（即投影点的投影路径与投影目标互相垂直，如果不垂直的话就是“斜投影”），台湾地区统一译作“投影”；

⑤ 一些词汇我按大众习惯进行缩写，比如使用“紧化”而非“紧致化”、“锥形”而非“锥流形”等；

⑥ 多数的 and 被我用顿号代替，这样看起来更直观。

序言

缩写

第一章导引

1.1 弦论之前的历史

1.2 弦论涉及到的问题

1.3 关于弦的历史展望

1.4 约定

引用文献

第二章经典弦论

2.1 点粒子

2.2 相对论弦

2.3 振子展开

2.3.1 闭弦

2.3.2 开弦

2.3.3 Virasoro(维拉宿 ) 约束

引用文献

练习

第三章玻色弦的量子化

3.1 协变正则量子化

3.2 光锥量子化

3.3 玻色弦的谱

3.4 非定向弦

3.4.1 开弦、Chan(陈 )-Paton( 佩顿 ) 因子

3.5 路径积分量子化

3.6 拓扑非平庸世界面

3.7 BRST 初步

3.8 弦论中的 BRST 、物理谱

引用文献

练习

第四章共形场论（CFT）

4.1 共形变换

4.1.1 二维情形

4.2 共形不变场论

4.3 径向量子化

4.4 模式展开

4.5 Virasoro 代数、中心荷

4.6 Hilbert( 希尔伯特 ) 空间

4.7 自由玻色子

4.8 自由费米子

4.9 共形反常

4.10 共形代数的表示

4.11 仿射流代数

4.12 自由费米子、 O(N) 仿射对称性

4.13 超共形对称性

4.13.1 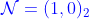${\color{Blue} \mathcal{N}=(1,0)_2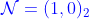}$ 超共形对称性

4.13.2 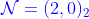${\color{Blue} \mathcal{N}=(2,0)_2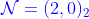}$ 超共形对称性

4.13.3 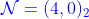${\color{Blue} \mathcal{N}=(4,0)_2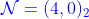}$ 超共形对称性

4.14 存在背景荷的标量

4.15 鬼的 CFT

4.16 圆盘上的 CFT

4.16.1 圆盘上的自由无质量玻色子

4.16.2 圆盘上的自由无质量费米子

4.16.3 射影平面

4.17 环面上的 CFT

4.18 紧标量

4.18.1 模不变性

4.18.2 退紧化

4.18.3 环面传播子

4.18.4 边缘形变

4.18.5 多重紧标量

4.18.6 强化对称性、弦 Brout( 布鲁特 )-Englert( 恩格勒特 )-Higgs( 希格斯 ) 效应

4.18.7 T-对偶

4.19 环面上的自由费米子

4.20 玻色化

4.20.1 玻色鬼系统的“玻色化”

4.21 轨形

4.22 Euler( 欧拉 ) 数为零的其他曲面上的 CFT

4.23 高亏格 Riemann( 黎曼 ) 曲面上的 CFT

引用文献

练习

第五章散射振幅和顶点算符

5.1 有关物理的顶点算符

5.2 三级快子振幅的计算

5.2.1 闭弦

5.2.2 开弦

5.3 一圈真空振幅

5.3.1 环面

5.3.2 圆柱体

5.3.3 Klein(克莱因 ) 瓶

5.3.4 Möbius(莫比乌斯 ) 带

5.3.5 蝌蚪消除

5.3.6 紫外结构、紫外-红外对应

引用文献

练习

第六章背景场中的弦

6.1 非线性 σ - 模型方法

6.2 对共形不变性的探索

6.3 线性胀子、 D < 26 维中的弦

6.4 非平庸背景中的 T- 对偶

引用文献

练习

第七章超弦和超对称

7.1 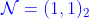${\color{Blue} \mathcal{N}=(1,1)_2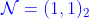}$ 世界面的超共形对称性

7.2 闭（第 II 型）超弦

7.2.1 无质量 R-R 态

7.3 第 I 型超弦

7.4 杂化弦

7.5 超弦顶点算符

7.6 一圈超弦真空振幅

7.6.1 第 IIA/B 型超弦

7.6.2 杂化超弦

7.6.3 第 I 型超弦

7.7 闭超弦和 T - 对偶

7.7.1 第 II 型弦论

7.7.2 杂化弦

7.8 超对称性的有效作用

7.9 反常

引用文献

练习

第八章 D-膜

8.1 反对称张量、 p - 膜

8.2 开弦、 T- 对偶

8.3 D- 膜

8.4 D- 膜、 R-R 荷

8.4.1 D-瞬子

8.5 D- 膜有效作用

8.5.1 Dirac(狄拉克 )-Born( 玻恩 )-Infeld( 英费尔德 ) 作用

8.5.2 与反常相关的项

8.6 多重膜、非 Abel( 阿贝尔 ) 对称性

8.7 T- 对偶、定向形

8.8 D- 膜是一种超引力孤子

8.8.1 超引力解

8.8.2 地平线、奇异性

8.8.3 极值膜及其近地平线几何

8.9 NS 5 - 膜

引用文献

练习

第九章紧化和对称性破缺

9.1 Naran( 纳兰 ) 紧化

9.2 世界面 v.s. 时空对称性

9.2.1 ${\color{Blue} \mathcal{N}=1_4}$ 时空对称性

9.2.2 ${\color{Blue} \mathcal{N}=2_4}$ 时空对称性

9.3 超对称的轨形约化

9.4 具有 ${\color{Blue} \mathcal{N}=2_4}$ 超对称性的杂化轨形

9.5 自发超对称性破缺

9.6 杂化 ${\color{Blue} \mathcal{N}=1_4}$ 轨形、四维中的手征性

9.7 Calabi( 卡拉比 )-Yau( 丘 ) 流形

9.7.1 绕异性

9.7.2 SU(3) 绕异性的结果

9.7.3 CY 模空间

9.8 ${\color{Blue} \mathcal{N}=1_4}$ 杂化紧化

9.8.1 低能 ${\color{Blue} \mathcal{N}=1_4}$ 杂化谱

9.9 第 II 型弦的 K3 紧化

9.10 第 II 型弦的 ${\color{Blue} \mathcal{N}=2_6}$ 轨形

9.11 第 II 型弦的 CY 紧化

9.12 镜像对称性

9.13 缺乏连续全局对称性

9.14 定向形

9.14.1 K3 定向形

9.14.2 Klein瓶振幅

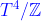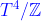9.14.3 ${\color{Blue} T^4/\mathbb{Z}}$ 上的 D- 膜

9.14.4 圆柱体振幅

9.14.5 Möbius带振幅

9.14.6 蝌蚪消除

9.14.7 开弦谱

9.15 轨形奇点处的 D- 膜

9.16 磁化紧化、相交膜

9.16.1 内磁场中的开弦

9.16.2 相交膜

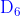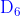9.16.3 相交 ${\color{Blue} \mathrm{D}_6}$ - 膜

9.17 标准模型在哪？

9.17.1 杂化弦

9.17.2 第 II 型弦论

9.17.3 第 I 型弦

9.18 统一

引用文献

练习

第十章弦有效耦合的圈修正

10.1 杂化规范阈值的计算

10.2 在壳红外正规化

10.2.1 阈值的估算

10.3 杂化引力阈值

10.4 一圈 Fayet( 法耶特 )-Iliopoulos( 李尔普罗斯 ) 项

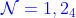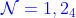10.5 阈值修正的 ${\color{Blue} \mathcal{N}=1,2_4}$ 示例

10.6 阈值的 ${\color{Blue} \mathcal{N}=2_4}$ 普适性

10.7 “重访”统一

引用文献

练习

第十一章对偶关系和非微扰效应

11.1 微扰关系

11.2 BPS 态与 BPS 边界

11.3 非重正定理、 BPS- 饱和耦合

11.4 第 IA 型 v.s. M- 理论

11.5 第 IIB 型弦的自偶

11.6 第 II 型弦论的 U- 对偶

11.6.1 U- 对偶与边界态

11.7 十维中的杂化 / 第 I 型弦

11.7.1 第 I 型 ${\color{Blue} \mathrm{D}_1}$ - 弦

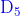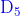11.7.2 第 I 型 ${\color{Blue} \mathrm{D}_5}$ - 膜

11.7.3 进一步的一致性检验

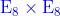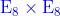11.8 M- 理论与 ${\color{Blue} \mathrm{E}_8\times\mathrm{E}_8}$ 杂化弦

11.8.1 强杂化耦合处的统一

11.9 六维中的杂化 / 第 II 型弦

11.9.1 规范对称性增强与奇异 K3 曲面

11.9.2 四维中的杂化 / 第 II 型对偶

11.10 锥形奇点与锥形转移

引用文献

练习

第十二章黑洞和弦论中的熵

12.1 简史

12.2 策略

12.3 黑洞热力学

12.3.1 Euclid(欧几里得 ) 延拓

12.3.2 Hawking(霍金 ) 蒸发和与灰体因子

12.4 信息问题与全息假说

12.5 五维极值带电黑洞

12.6 五维非极值 RN 黑洞

12.7 近地平线区域

12.8 Hawking 速率的半经典推导

12.9 微观实现

12.9.1 边界态的世界体积理论

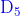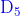12.9.2 ${\color{Blue} \mathrm{D}_1}$ - ${\color{Blue} \mathrm{D}_5}$ 边界态的低能 SCFT

12.9.3 熵的微观计算

12.9.4 Hawking 蒸发速率的微观推导

12.10 尾声

引用文献

练习

第十三章体/边对应

13.1 大 N 规范理论与弦论

13.2 退耦原理

13.3 近地平线极限

13.4 对应的要素

13.5 体场、边界算符

13.6 全息

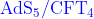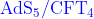13.7 测试 ${\color{Blue} \mathrm{AdS}_5/\mathrm{CFT}_4}$ 对应

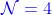13.7.1 ${\color{Blue} \mathcal{N}=4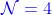}$ 规范理论的手征谱

13.7.2 与弦论谱匹配

13.7.3 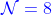${\color{Blue} \mathcal{N}=8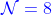}$ 五维规范超引力

13.7.4 受保护关联函数、反常

13.8 关联函数

13.8.1 两点函数

13.8.2 三点函数

13.8.3 引力作用、共形反常

13.9 Wilson( 威尔逊 ) 圈

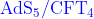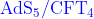13.10 有限温下的 ${\color{Blue} \mathrm{AdS}_5/\mathrm{CFT}_4}$ 对应

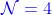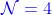13.10.1 有限温下的 ${\color{Blue} \mathcal{N}=4}$ 超 Yang( 杨 )-Mills( 米尔斯 ) 理论

13.10.2 黑 ${\color{Blue} \mathrm{D}_3}$ 膜的近地平线极限

13.10.3 有限体积和大 N 相变

13.10.4 热全息物理

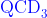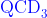13.10.5 （某一版本的） ${\color{Blue} \mathrm{QCD}_3}$ 中的空间 Wilson 圈

13.10.6 胶球质量谱

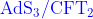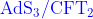13.11 ${\color{Blue} \mathrm{AdS}_3/\mathrm{CFT}_2}$ 对应

13.11.1 “重访”灰体因子

13.12 全息重正化群

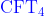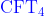13.12.1 ${\color{Blue} \mathrm{CFT}_4}$ 的微扰

13.12.2 畴壁、流方程

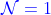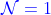13.12.3 保 ${\color{Blue} \mathcal{N}=1}$ 对称性的 RG 流

13.13 Randall( 兰德尔 )-Sundrum( 桑德鲁姆 ) 几何

13.13.1 紧化的一种替代方法

引用文献

练习

第十四章弦论和矩阵模型

14.1 M(atrix) 模型

14.1.1 膜（ membrane ）量子化

14.1.2 第 IIA 型 ${\color{Blue} \mathrm{D}_0}$ - 膜、 DLCQ

14.1.3 M(atrix) 理论中的引力和膜

14.1.4 从 M(atrix) 理论到二引力相互作用

14.2 矩阵模型和 D=1 玻色弦论

14.2.1 连续极限

14.2.2 求解矩阵模型

14.2.3 双标度极限

14.2.4 自由费米子绘景

14.3 D=1 弦论的矩阵描述

14.3.1 矩阵量子力学、线上的自由费米子

14.3.2 连续极限

14.3.3 双标度极限

14.3.4 D-粒子、快子、全息

引用文献

练习

附录 A：二维复几何

附录 B：微分形式

附录 C：theta 和其他椭圆函数

C.1 ϑ 及其相关函数

C.2 Weierstrass( 魏尔斯特拉斯 ) 函数

C.3 模形式

C.4 Poisson( 泊松 ) 重求和

附录 D：环面格求和

附录 E：环面 Kaluza(卡鲁扎)-Klein 约化

附录 F：Reissner(赖斯纳)-Nordström(努德斯特伦) 黑洞

附录 G：D=4 中的电磁对偶

附录 H：十维与七维中的超对称作用

H.1 ${\color{Blue} \mathcal{N}=1_{11}}$ 超引力

H.2 第 IIA 型超引力

H.3 第 IIB 型超引力

H.4 第 II 型超引力：民主表述

H.5 ${\color{Blue} \mathcal{N}=1_{10}}$ 超对称

附录 I：与物质耦合的 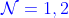${\color{Blue} \mathcal{N}=1,2}$ 四维超引力

I.1 ${\color{Blue} \mathcal{N}=1_4}$ 超引力

I.2 ${\color{Blue} \mathcal{N}=2_4}$ 超引力

附录 J：四维中的 BPS 多重态

附录 K：反 de Sitter(德西特) 空间的几何学

K.1 Minkowski( 闵可夫斯基 ) 符号 AdS

K.2 Euclidean AdS

K.3 平直空间的共形结构

K.4 AdS 中的场

K.4.1 Poincaré( 庞加莱 ) 坐标中的波方程

K.4.2 体-边传播子

K.4.3 体到体传播子

引用文献

索引

Elias Kiritsis《String Theory in a Nutshell》（埃利亚斯·基里西斯《简明弦论》）中文目录

第一章 导引

第二章 经典弦论

第三章 玻色弦的量子化

第四章 共形场论（CFT）

第五章 散射振幅和顶点算符

第六章 背景场中的弦

第七章 超弦和超对称

第八章 D-膜

第九章 紧化和对称性破缺

第十章 弦有效耦合的圈修正

第十一章 对偶关系和非微扰效应

第十二章 黑洞和弦论中的熵

第十三章 体/边对应

第十四章 弦论和矩阵模型

附录 A：二维复几何

附录 B：微分形式

附录 C：theta 和其他椭圆函数

附录 D：环面格求和

附录 E：环面 Kaluza(卡鲁扎)-Klein 约化

附录 F：Reissner(赖斯纳)-Nordström(努德斯特伦) 黑洞

附录 G：D=4 中的电磁对偶

附录 H：十维与七维中的超对称作用

附录 I：与物质耦合的 四维超引力

附录 J：四维中的 BPS 多重态

附录 K：反 de Sitter(德西特) 空间的几何学

第一章导引

第二章经典弦论

第三章玻色弦的量子化

第四章共形场论（CFT）

第五章散射振幅和顶点算符

第六章背景场中的弦

第七章超弦和超对称

第九章紧化和对称性破缺

第十章弦有效耦合的圈修正

第十一章对偶关系和非微扰效应

第十二章黑洞和弦论中的熵

第十三章体/边对应

第十四章弦论和矩阵模型

附录 I：与物质耦合的 ${\color{Blue} \mathcal{N}=1,2}$ 四维超引力