编译原理实验2——语法分析(C++代码实现)

一 、实验目的

语法分析是编译程序中的核心部分。本实验通过设计一个典型的自顶向下语法分析程序——LL(1) 语法分析程序，进一步理解并掌握语法分析的原理和实现技术。

二 、实验原理

语法分析的主要任务是“组词成句”，将词法分析给出的单词序列按语法规则构成更大的语法单位，如“程序、语句、表达式”等；或者说，语法分析的作用是用来判断给定输入串是否为合乎文法的句子。
按照生成语法树的方向不同，常用的语法分析方法有两类：自顶向下分析和自底向上分析。自顶向下分析也称面向目标的分析方法，也就是从文法的开始符出发，试图推导出与输入单词串相匹配的句子。自底向上分析也称移进-归约分析方法，从输入单词串开始，试图归约到文法的开始符。
预测分析法（LL(1)方法）的基本思想是：从文法开始符S 出发，从左到右扫描源程序，每次通过向前查看 1 个字符，选择合适的产生式，生成句子的最左推导。

三 、实验步骤与要求

1、 复习教材第4章，进一步理解LL(1)方法的原理和实现技术。根据预测分析程序的框图（教材P94-图5.11），编写一个语法分析程序。可根据自己的能力选择以下三项（由易到难）之一作为分析算法的输入：
(1)根据文法，人工构造分析表M，直接输入表M。
(2)输入文法的FIRST集和FOLLOW集，由程序自动生成该文法的预测分析表M。
(3)输入文法，由程序自动生成该文法的预测分析表M。
2、 程序具有通用性，即所编制的LL（1）语法分析程序能够适用于不同文法以及各种输入单词串。
3、 有运行实例。对于输入的一个文法和一个单词串，语法分析程序应能正确地判断此单词串是否为该文法的句子，并要求输出分析过程。
4、 设计合理的数据结构，特别是文法、预测分析表、分析栈等的存储结构。

四、实验代码

//#include "pch.h"
#include <iostream>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<stack>
using namespace std;
void GramF();//分解产生式程序
void GramIn();//文法输入程序
void WordIn();//文字输入程序
bool Is(char x, char a[], int n); //是否在集合中
void GetFirst(char a);//first集求解程序
void ADD(string& a, string& b);//集合相加程序
void ADDfollow(string& a, string& b);//集合(follow)相加程序
int Back(char a);//根据字母返回下标程序
void GetFollow(char a);//follow集求解程序
bool IsChar(char a, string b);//判断一个字符是否在一个集合中的程序
void FAtable();//预测分析表构建程序
void GAnalysis();//文法分析程序
void clearF();//净化程序
void cc();
//i + ( ) *  A B C D E    A->BC C->+BC|@ B->DE E->*DE|@ D->(A)|i

int table[100][100] = { 0 };//预测表
char Vt[100] = { "" };//终结符
char Vn[100] = { "" };//非终结符
string Generative[100] = { "" };//文法产生式存储
string GenerativeNew[100] = { "" };//文法产生式分解后的存储
string first[100] = { "" };//first集合
string follow[100] = { "" };//follow集合
char word[100] = { "" };//待测试的文字
int VtNum = 0;//终结符号的个数
int VnNum = 0;//非终结符号的个数
int GenNum = 0;//文法产生式个数
int GenNumNew = 0;//文法产生式分解后的个数
stack<char> st;//预测分析栈

void cc() {
    int i, j, k, q, p;
    for (i = 0; i < VnNum; i++) {
        j = 0;
        while (first[i][j] != '\0') {
            k = j + 1;
            while (first[i][k] != '\0') {
                if (first[i][j] == first[i][k])
                    first[i][k] = ' ';
                k++;
            }
            j++;
        }
        q = 0;
        while (first[i][q] != '\0') {
            if (first[i][q] != ' ') {
                break;
            }
            else {
                p = q + 1;
                while (first[i][p] != ' ') {
                    if (first[i][p] == '\0')
                        break;
                    else {
                        first[i][q] = first[i][p];
                        first[i][p] = ' ';
                    }
                }
            }
            q++;
        }
        q = 0;
        while (first[i][q] != '\0') {
            if (first[i][q] == ' ')
                first[i][q] = '\0';
            q++;
        }
    }
}
/************分解文法产生式程序*************/
void GramF() {
    int j, z = 0, x;
    for (int i = 0; i < GenNum; i++) {
        x = 0;
        while (1) {
            char ch1 = Generative[i][x];
            if (ch1 == '\0' || ch1 == '|')
                break;
            GenerativeNew[z] += Generative[i][x];
            x++;
        }
        z++;
        j = 0;
        while (Generative[i][j] != '\0') {
            if (Generative[i][j] == '|') {
                j++;
                for (x = 0; x < 3; x++) {
                    GenerativeNew[z] += Generative[i][x];
                }
                while (1) {
                    char ch2 = Generative[i][j];
                    if (ch2 == '\0' || ch2 == '|')
                        break;
                    GenerativeNew[z] += Generative[i][j];
                    j++;
                }
                z++;
            }
            else {
                j++;
            }
        }
    }
    GenNumNew = z;
}
/************文法输入程序*************/
void GramIn() {
    int i = 0;
    printf("请输入终结符号：\n");
    scanf_s("%c", Vt + i,1);
    while (*(Vt + i) != '\n') {
        i++;
        scanf_s("%c", Vt + i,1);
    }
    Vt[i] = '#';
    i++;
    VtNum = i;//输入结束存储终结符号个数

    i = 0;//初始化i值准备输入非终结符号
    printf("请输入非终结符号：\n");
    scanf_s("%c", Vn + i,1);
    while (*(Vn + i) != '\n') {
        i++;
        scanf_s("%c", Vn + i,1);
    }
    VnNum = i;//输入结束存储非终结符号个数

    i = 0;//初始化i值准备输入文法产生式
    printf("请输入文法产生式：\n");
    char ch;
    while (cin >> Generative[i]) {
        i++;
        if ((ch = getchar()) == '\n')
            break;
    }
    GenNum = i;//输入结束存储文法产生式个数
}
/************文字输入程序*************/
void WordIn() {
    printf("请输入您需要测试的文字：\n");
    int i = 0;
    //getchar();
    scanf_s("%c", word + i);
    while (*(word + i) != '\n') {
        i++;
        scanf_s("%c", word + i);
    }
}
/************是否在集合中*************/
bool Is(char x, char a[], int n) {
    for (int i = 0; i < n; i++) {
        if (a[i] == x)
            return true;
    }
    return false;
}
/************first集求解程序*************/
void GetFirst(char a) {
    int k = 0;
    for (int i = 0; i < GenNumNew; i++) {
        if (GenerativeNew[i][0] != a)
            continue;
        if (Is(GenerativeNew[i][3], Vt, VtNum)) {
            //如果该非终结符产生式右部第一个字符是终结符号,则直接将其计入左部非终结符的FIRST集
            first[Back(GenerativeNew[i][0])] += GenerativeNew[i][3];
        }
        else if (Is(GenerativeNew[i][3], Vn, VnNum)) {
            //如果该非终结符号右部第一个字符是非终结符号,则对该右部第一个字符的FIRST进行求解,并将其加入左部字符的FIRST集
            GetFirst(GenerativeNew[i][3]);
            ADD(first[Back(GenerativeNew[i][0])], first[Back(GenerativeNew[i][3])]);
        }
        else if (GenerativeNew[i][3] == '@') {
            //如果该非终结符产生式是个空,则将空加入左部字符的FIRST集
            int j = 0;
            while (first[Back(GenerativeNew[i][0])][j] != '\0') {
                if (first[Back(GenerativeNew[i][0])][j] == '@') {
                    k = 1;
                    break;
                }
                j++;
            }
            if (!k)
                first[Back(GenerativeNew[i][0])] += '@';
        }
    }
}
/************follow集清除重复元素程序*************/
void clearF() {
    int i, j, k, q, p;
    //下面是清除follow集
    for (i = 0; i < VnNum; i++) {
        j = 0;
        while (follow[i][j] != '\0') {
            k = j + 1;
            while (follow[i][k] != '\0') {
                if (follow[i][j] == follow[i][k])
                    follow[i][k] = ' ';
                k++;
            }
            j++;
        }
        q = 0;
        p = 0;
        while (follow[i][q] != '\0') {
            if (follow[i][q] != ' ') {
                break;
            }
            else {
                p = q + 1;
                while (follow[i][p] != ' ') {
                    if (follow[i][p] == '\0')
                        break;
                    else {
                        follow[i][q] = follow[i][p];
                        follow[i][p] = ' ';
                    }
                }
            }
            q++;
        }
        q = 0;
        while (follow[i][q] != '\0') {
            if (follow[i][q] == ' ')
                follow[i][q] = '\0';
            q++;
        }
    }
}
/************集合相加程序*************/
void ADD(string& a, string& b) {
    int i = 0, zk = 1, j = 0;
    while (b[j] != '\0') {
        i = 0;
        zk = 1;
        while (a[i] != '\0') {
            if (b[j] == a[i] || b[j] == '@') {
                zk = -1;
                break;
            }
            i++;
        }
        if (zk == 1)
            a += b[j];
        j++;
    }
}
/************集合(follow)相加程序*************/
void ADDfollow(string& a, string& b) {
    int i = 0, zk = 1, j = 0;
    while (b[j] != '\0') {
        i = 0;
        zk = 1;
        while (a[i] != '\0') {
            if (b[j] == a[i]) {
                zk = -1;
                break;
            }
            i++;
        }
        if (zk == 1)
            a += b[j];
        j++;
    }
}
/************follow集求解程序*************/
void GetFollow(char a) {
    int i = Back(a), j;
    //if (i == 0 || i == 1 || i == 2 || i == 3) {
        //如果待求解字符是开始字符,则把'#'加入其FOLLOW集
        //if (IsChar(a, follow[Back(a)]))
            follow[Back(a)] += '#';
        for (j = 0; j < GenNumNew; j++) {
            if (GenerativeNew[j][3] == a && GenerativeNew[j][4] != '\0') {//如果是A->Bb
                if (Is(GenerativeNew[j][4], Vt, VtNum)) {//如果b是终结符号，直接加入follow(B)
                    if (IsChar(GenerativeNew[j][4], follow[Back(a)]))//判断b是否在follow(B)中
                        continue;
                    else
                        follow[Back(a)] += GenerativeNew[j][4];
                }
                else if (Is(GenerativeNew[j][4], Vn, VnNum)) {//如果b是非终结符号，需要判断
                    if (IsChar('@', first[Back(GenerativeNew[j][4])])) {//如果b可以推出空'@'，则需要将follow(A)加入follow(B)
                        GetFollow(GenerativeNew[j][0]);
                        ADDfollow(follow[Back(a)], follow[Back(GenerativeNew[j][0])]);
                    }
                    ADD(follow[Back(a)], first[Back(GenerativeNew[j][4])]);
                }
            }
            else if (GenerativeNew[j][4] == a && GenerativeNew[j][5] != '\0') {//如果是A->aBb
                if (Is(GenerativeNew[j][5], Vt, VtNum)) {//如果b是终结符号，直接加入follow(B)
                    if (IsChar(GenerativeNew[j][5], follow[Back(a)]))//判断b是否在follow(B)中
                        continue;
                    else
                        follow[Back(a)] += GenerativeNew[j][5];
                }
                else if (Is(GenerativeNew[j][5], Vn, VnNum)) {//如果b是非终结符号，需进行判断
                    if (IsChar('@', first[Back(GenerativeNew[j][5])])) {//如果b可以推出空'@'，则需要将follow(A)加入follow(B)
                        GetFollow(GenerativeNew[j][0]);
                        ADDfollow(follow[Back(a)], follow[Back(GenerativeNew[j][0])]);
                    }
                    ADD(follow[Back(a)], first[Back(GenerativeNew[j][5])]);
                }
            }
            else if (GenerativeNew[j][4] == a && GenerativeNew[j][5] == '\0') {//如果是A->aB
                GetFollow(GenerativeNew[j][0]);//直接将follow(A)加入follow(B)
                ADDfollow(follow[Back(a)], follow[Back(GenerativeNew[j][0])]);
            }
        }
    //}
}
/************判断一个字符是否在一个集合中的程序*************/
bool IsChar(char a, string b) {
    int i = 0;
    while (b[i] != '\0') {
        if (a == b[i])
            return true;
        i++;
    }
    return false;
}
/************预测分析表构建程序*************/
void FAtable() {
    int i, j;
    for (i = 0; i < VtNum; i++) {
        for (j = 0; j < GenNumNew; j++) {
            if (Vt[i] == GenerativeNew[j][3])
                //如果终结符Vt[i]在A->a的first(a)中,则将A->a放入table[A,Vt[i]]中
                table[Back(GenerativeNew[j][0])][i] = j;
            else if (Is(GenerativeNew[j][3], Vn, VnNum)) {
                if (IsChar(Vt[i], first[Back(GenerativeNew[j][3])])) {
                    table[Back(GenerativeNew[j][0])][i] = j;
                }
            }
            else if (GenerativeNew[j][3] == '@') {
                //如果当前的产生式是：A->a且，a='@'，则判断当前的Vt[i]是否在
                if (IsChar(Vt[i], follow[Back(GenerativeNew[j][0])])) {
                    table[Back(GenerativeNew[j][0])][i] = j;
                }
            }
        }
    }
}
/************根据字母返回终结符下标程序*************/
int BBack(char a) {
    for (int i = 0; i < VtNum; i++) {
        if (a == Vt[i])
            return i;
    }
    return -1;
}
/************根据字母返回非终结符下标程序*************/
int Back(char a) {
    for (int i = 0; i < VnNum; i++) {
        if (a == Vn[i])
            return i;
    }
    return -1;
}
/************文法分析程序*************/
void GAnalysis() {
    int i = 0, x, y, k, error = 0, n = 1;
    char a;
    string chan = "";
    st.push('#');
    st.push(Vn[0]);
    a = st.top();
    while (!(a == word[i] && a == '#')) {
        if (Is(st.top(), Vn, VnNum)) {
            x = Back(st.top());
            y = BBack(word[i]);
            k = table[x][y];//获得产生式
            if (k == -1) {
                error++;
                cout << "步骤[" << n << "]：识别错误！跳过" << word[i] << "；\n";
                n++;
                i++;
                break;
            }
            else {
                chan = GenerativeNew[k];
                k = 0;
                st.pop();
                while (chan[k] != '\0') {
                    k++;
                }
                k--;
                if (chan[k] != '@') {
                    while (chan[k] != '>') {
                        st.push(chan[k]);
                        k--;
                    }
                    //i++;
                    cout << "步骤[" << n << "]：用" << chan << "的右部分逆序入栈已经完成；\n";
                    n++;
                }
                else {
                    cout << "步骤[" << n << "]：用" << chan << "；\n";
                    n++;
                    //i++;
                }
            }
        }
        else if (Is(st.top(), Vt, VtNum)) {
            if (st.top() == word[i]) {
                cout << "步骤[" << n << "]：匹配栈顶和当前符号" << word[i] << "，成功；\n";
                st.pop();
                i++;
                n++;
            }
            else {
                cout << "步骤[" << n << "]：识别失败！！\n";
                n++;
                break;
            }
        }
        a = st.top();
    }
    if (error) {
        cout << "步骤[" << n << "]：识别错误！！错误跳过次数：" << error << "\n";
        n++;
    }
    else {
        cout << "步骤[" << n << "]：识别成功！！\n";
        n++;
    }
}
void ChuShi() {
    for (int i = 0; i < 100; i++) {
        for (int j = 0; j < 100; j++) {
            table[i][j] = -1;
        }
    }
}
int main() {
    using std::cout;
    cout.setf(std::ios::left);
    ChuShi();//初始化二维数组
    GramIn();//输入非终结、终结字符和文法产生式
    GramF();//文法产生式分析完毕
    int i, j;
    for (i = 0; i < VnNum; i++) {//first集合
        GetFirst(Vn[i]);
    }
    cc();
    for (i = 0; i < VtNum; i++) {//follow集合
        GetFollow(Vn[i]);
    }
    clearF();//清除follow集合
    FAtable();//预测分析表
    cout << "非终结符的first集为：\n";
    for (i = 0; i < VnNum; i++) {
        cout << "FIRST(" << Vn[i] << ")：" + first[i] << endl;
    }
    cout << "非终结符的follow集为：\n";
    for (i = 0; i < VnNum; i++) {
        cout << "FOLLOW(" << Vn[i] << ")：" + follow[i] << endl;
    }
    cout << "预测分析表为：\n";
    cout << "\t";
    cout.width(7);
    for (i = 0; i < VtNum; i++) {
        cout << Vt[i];
        cout.width(7);
    }
    cout << endl;

    for (i = 0; i < VnNum; i++) {
        cout << Vn[i];
        cout.width(7);
        for (j = 0; j < VtNum; j++) {
            cout << GenerativeNew[table[i][j]];
            cout.width(7);
        }
        cout << endl;
    }
    WordIn();
    cout << "识别结果如下：\n";
    GAnalysis();
    return 0;
}

五、测试用例

1.测试数据(从终端需要输入的数据)：
(1)首先输入终结符号：
i + ( ) *
(2)接着输入非终结符号：
A B C D E
(3)最后输入文法产生式(注意：文法产生式之间用空格隔开，不要换行)：
A->BC C->+BC|@ B->DE E->DE|@ D->(A)|i
2.对应数据产生的FIRST和FOLLOW集：
(1)FIRST集合：
FIRST(A)：{(,i}
FIRST(B)：{(,i}
FIRST©：{+,@}
FIRST(D)：{(,i}
FIRST(E)：{,@}
(2)FOLLOW集合：
FOLLOW(A)：{#,)}
FOLLOW(B)：{#,),+}
FOLLOW©：{#,)}
FOLLOW(D)：{#,),+,*}
FOLLOW(E)：{#,),+}
3.对应数据产生的预测分析表：

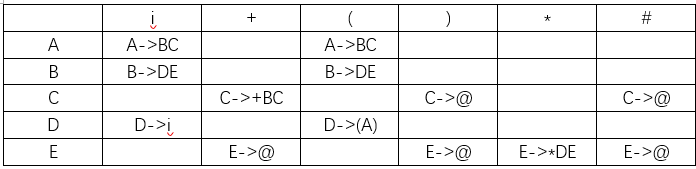
4.测试输入的字符串(正确格式)：

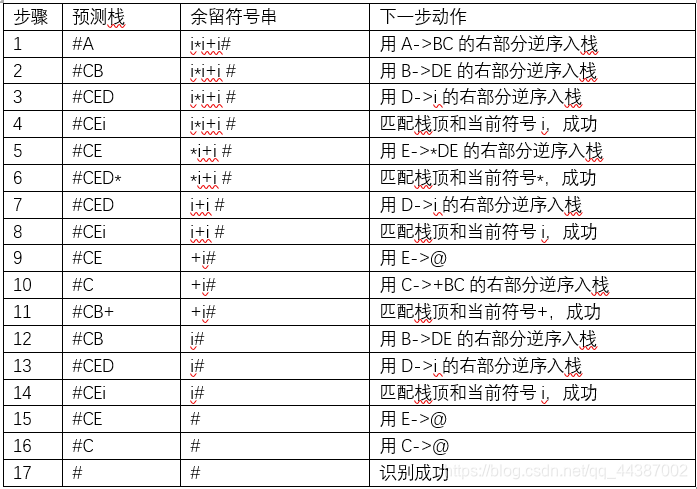
i*i+i#

5.求解所得结果