文章目录
前言
一、多元线性回归
1、问题描述
在多元线性回归中,我们的目标是使用一组输入变量(或特征) x 1 , x 2 , . . . , x D x_1, x_2, ..., x_D x1,x2,...,xD 来预测一个输出变量 y y y。
2、模型建模
对于第 i i i条数据,其回归方程可以表示为:
y i = w 0 + w 1 x i 1 + w 2 x i 2 + . . . + w D x i D + ϵ i \begin{equation} y_i = w_0 + w_1 x_{i1} + w_2 x_{i2} + ... +w_D x_{iD} + \epsilon_i \end{equation} yi=w0+w1xi1+w2xi2+...+wDxiD+ϵi
其中, w j w_j wj 是第 j j j 个回归系数, ϵ i \epsilon_i ϵi 是第 i i i 个观察的误差项。 w 0 w_0 w0 是截距项,也可以看作是当所有输入都为0时的输出。
误差项: 我们假设误差项
ϵ
i
\epsilon_i
ϵi 服从均值为0、方差为
β
−
1
\beta^{-1}
β−1 的高斯分布,即
ϵ
i
∼
N
(
0
,
β
−
1
)
\begin{equation} \epsilon_i \sim \mathcal{N}(0, \beta^{-1}) \end{equation}
ϵi∼N(0,β−1)
这个假设意味着我们的模型预测有误差,且这些误差是随机的、独立的,并且遵循正态分布。
基函数: 在多元线性回归中,我们还可以引入基函数 ϕ ( x ) \phi(x) ϕ(x),以便我们可以对输入进行非线性转换。在这种情况下,我们的模型变为:
y i = w 0 + w 1 ϕ 1 ( x i ) + w 2 ϕ 2 ( x i ) + . . . + w D ϕ D ( x i ) + ϵ i \begin{equation} y_i =w_0 + w_1 \phi_1(x_i) + w_2 \phi_2(x_i) + ... + w_D \phi_D(x_i) + \epsilon_i \end{equation} yi=w0+w1ϕ1(xi)+w2ϕ2(xi)+...+wDϕD(xi)+ϵi
这使我们可以使用线性模型来拟合非线性关系。定义
ϕ
0
(
x
)
=
1
\phi_0(x)=1
ϕ0(x)=1 ,其可以简单的表示为:
y
i
=
∑
j
=
0
D
w
j
ϕ
j
(
x
i
)
+
ϵ
i
\begin{equation} y_i = \sum_{j=0}^{D} w_j \phi_j(x_i) + \epsilon_i \end{equation}
yi=j=0∑Dwjϕj(xi)+ϵi
这里我们并不关心基函数是什么,并不影响模型的求解,常见的基函数有:
- 高斯基函数
ϕ j ( x ) = e x p { − ( x − μ j ) 2 2 s 2 } \begin{equation} \phi_j(x) = exp\{-\frac{(x-\mu_j)^2}{2s^2}\} \end{equation} ϕj(x)=exp{−2s2(x−μj)2} - Sigmoid 基函数
ϕ
j
(
x
)
=
1
1
+
e
x
p
{
−
(
x
−
μ
j
)
/
s
}
\begin{equation} \phi_j(x) = \frac{1}{1 + exp\{-(x-\mu_j)/s\}} \end{equation}
ϕj(x)=1+exp{−(x−μj)/s}1
3. 双曲正切函数,简称 Tanh,
t
a
n
h
(
x
)
=
2
σ
(
2
x
)
−
1
tanh(x)=2 \sigma(2x)-1
tanh(x)=2σ(2x)−1
ϕ
(
x
)
=
tanh
(
x
)
=
e
x
p
{
(
x
−
μ
j
)
/
s
}
−
e
x
p
{
−
(
x
−
μ
j
)
/
s
}
e
x
p
{
(
x
−
μ
j
)
/
s
}
+
e
x
p
{
−
(
x
−
μ
j
)
/
s
}
\begin{equation} \phi(x) = \tanh(x) = \frac{exp\{(x-\mu_j)/s\} - exp\{-(x-\mu_j)/s\}}{exp\{(x-\mu_j)/s\} + exp\{-(x-\mu_j)/s\}} \end{equation}
ϕ(x)=tanh(x)=exp{(x−μj)/s}+exp{−(x−μj)/s}exp{(x−μj)/s}−exp{−(x−μj)/s}
3、问题求解
3.1 精确解
已知: t = y ( x , w ) + ϵ t=y(x,w)+\epsilon t=y(x,w)+ϵ, ϵ ∼ \epsilon\sim ϵ∼是一个高斯噪声 ϵ ∼ N ( 0 , β − 1 ) \epsilon\sim \mathcal{N}(0, \beta^{-1}) ϵ∼N(0,β−1),样本 X = { x 1 , ⋅ ⋅ ⋅ , x N } , t = { t 1 , ⋅ ⋅ ⋅ , t N } = { t n ∣ n = 1 ⋅ ⋅ ⋅ N } X=\{x_1,\cdot\cdot\cdot,x_N\},t=\{t_1,\cdot\cdot\cdot,t_N\}=\{t_n|n=1\cdot\cdot\cdot N\} X={x1,⋅⋅⋅,xN},t={t1,⋅⋅⋅,tN}={tn∣n=1⋅⋅⋅N}
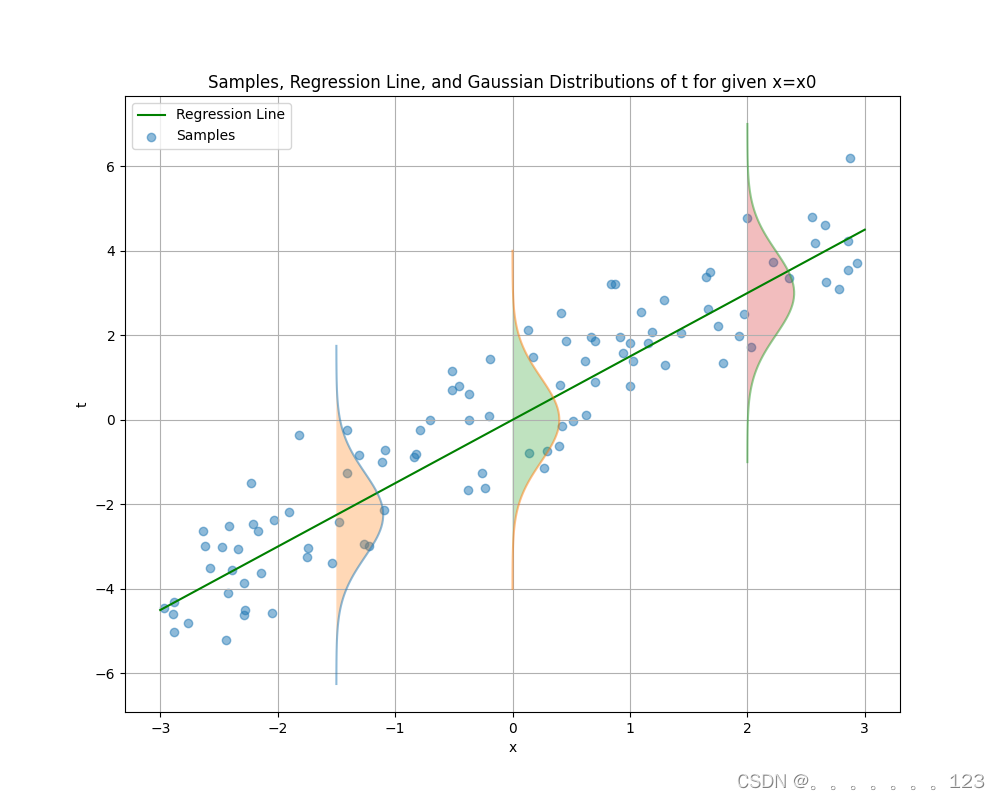
因为 ϵ \epsilon ϵ 是高斯分布的,所以 t t t 也会是高斯分布的,因为 t t t 是由 y ( x , w ) y(x, w) y(x,w) 和 ϵ \epsilon ϵ 的和构成的,而 y ( x , w ) y(x, w) y(x,w) 是确定的,不会引入额外的随机性,即:
p ( t ∣ x , w , β ) = N ( t ∣ y ( x , w ) , β − 1 ) \begin{equation} p(t|x,w,\beta) = \mathcal{N}(t|y(x,w), \beta^{-1}) \end{equation} p(t∣x,w,β)=N(t∣y(x,w),β−1)
当
ϕ
i
(
x
i
)
=
x
i
\phi_i(x_i)=x_i
ϕi(xi)=xi时,
t
t
t在给定的
x
x
x的情况下是服从
N
(
t
∣
y
(
x
,
w
)
,
β
−
1
)
\mathcal{N}(t|y(x,w), \beta^{-1})
N(t∣y(x,w),β−1)
那么在给定数据集
X
X
X和
t
t
t的情况下,其释然函数为:
p
(
t
∣
X
,
w
,
β
)
=
∏
n
=
1
N
N
(
t
n
∣
w
T
ϕ
(
x
n
)
,
β
−
1
)
\begin{equation} p(t|X,w,\beta) = \prod\limits^{N}_{n=1}\mathcal{N}(t_n|w^T\phi(x_n), \beta^{-1}) \end{equation}
p(t∣X,w,β)=n=1∏NN(tn∣wTϕ(xn),β−1)
使用极大释然估计的方法求参数
w
w
w和
β
\beta
β,那么对释然函数的对数求其最大时的参数
w
w
w和
β
\beta
β,即:
ln p ( t ∣ X , w , β ) = ∑ n = 1 N ln N ( t n ∣ w T ϕ ( x n ) , β − 1 ) = − N 2 ln ( 2 π ) + N 2 ln ( β − 1 2 ∑ n = 1 N β { t n − w T ϕ ( x n ) } 2 \begin{equation} \begin{align*} \text{ln}p(t|X,w,\beta) &= \sum\limits^{N}_{n=1}\text{ln}\mathcal{N}(t_n|w^T\phi(x_n), \beta^{-1}) \\ &= -\frac{N}{2}\ln(2\pi) + \frac{N}{2}\ln(\beta - \frac{1}{2}\sum\limits_{n=1}^{N}\beta\{t_n - w^T\phi(x_n)\}^2 \end{align*} \end{equation} lnp(t∣X,w,β)=n=1∑NlnN(tn∣wTϕ(xn),β−1)=−2Nln(2π)+2Nln(β−21n=1∑Nβ{tn−wTϕ(xn)}2
求解w
此时我们发现求参数
w
w
w时即最小化
E
D
(
w
)
=
1
2
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
n
)
}
2
E_D(w)=\frac{1}{2}\sum\limits_{n=1}^{N}\{t_n - w^T\phi(x_n)\}^2
ED(w)=21n=1∑N{tn−wTϕ(xn)}2,其实就等价于最小化MSE均方误差。那么
ln
p
(
t
∣
X
,
w
,
β
)
\text{ln}p(t|X,w,\beta)
lnp(t∣X,w,β)对
w
w
w的梯度为:
∇
ln
p
(
t
∣
X
,
w
,
β
)
=
β
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
)
}
ϕ
(
x
n
)
T
\begin{equation} \nabla\text{ln}p(t|X,w,\beta)=\beta\sum\limits_{n=1}^{N}\{t_n - w^T\phi(x)\}\phi(x_n)^T \end{equation}
∇lnp(t∣X,w,β)=βn=1∑N{tn−wTϕ(x)}ϕ(xn)T
令导数等于0
∇
ln
p
(
t
∣
X
,
w
,
β
)
=
β
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
n
)
}
ϕ
(
x
n
)
T
=
0
\begin{equation} \nabla\text{ln}p(t|X,w,\beta)=\beta\sum\limits_{n=1}^{N}\{t_n - w^T\phi(x_n)\}\phi(x_n)^T=0 \end{equation}
∇lnp(t∣X,w,β)=βn=1∑N{tn−wTϕ(xn)}ϕ(xn)T=0
我们可以进行如下推导以求解
w
w
w:
∑ n = 1 N t n ϕ ( x n ) T − ∑ n = 1 N w T ϕ ( x n ) ϕ ( x n ) T = 0 \begin{equation} \sum_{n=1}^{N} t_n\phi(x_n)^T - \sum_{n=1}^{N} w^T\phi(x_n)\phi(x_n)^T = 0 \end{equation} n=1∑Ntnϕ(xn)T−n=1∑NwTϕ(xn)ϕ(xn)T=0
∑ n = 1 N t n ϕ ( x n ) T − w T ( ∑ n = 1 N ϕ ( x n ) ϕ ( x n ) T ) = 0 \begin{equation} \sum_{n=1}^{N} t_n\phi(x_n)^T - w^T\left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T\right) = 0 \end{equation} n=1∑Ntnϕ(xn)T−wT(n=1∑Nϕ(xn)ϕ(xn)T)=0
w T ( ∑ n = 1 N ϕ ( x n ) ϕ ( x n ) T ) = ∑ n = 1 N t n ϕ ( x n ) T \begin{equation} w^T\left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T\right) = \sum_{n=1}^{N} t_n\phi(x_n)^T \end{equation} wT(n=1∑Nϕ(xn)ϕ(xn)T)=n=1∑Ntnϕ(xn)T
w
=
(
∑
n
=
1
N
ϕ
(
x
n
)
ϕ
(
x
n
)
T
)
−
1
∑
n
=
1
N
t
n
ϕ
(
x
n
)
\begin{equation} w = \left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T\right)^{-1} \sum_{n=1}^{N} t_n\phi(x_n) \end{equation}
w=(n=1∑Nϕ(xn)ϕ(xn)T)−1n=1∑Ntnϕ(xn)
我们把它写成矩阵的形式,令
Φ
=
{
ϕ
(
x
1
)
T
,
ϕ
(
x
2
)
T
,
⋅
⋅
⋅
,
ϕ
(
x
n
)
T
}
T
\Phi=\{\phi(x_1)^T, \phi(x_2)^T,\cdot\cdot\cdot,\phi(x_n)^T\}^T
Φ={ϕ(x1)T,ϕ(x2)T,⋅⋅⋅,ϕ(xn)T}T
Φ
=
[
ϕ
0
(
x
1
)
ϕ
1
(
x
1
)
⋯
ϕ
D
(
x
1
)
ϕ
0
(
x
2
)
ϕ
1
(
x
2
)
⋯
ϕ
D
(
x
2
)
⋮
⋮
⋱
⋮
ϕ
0
(
x
N
)
ϕ
1
(
x
N
)
⋯
ϕ
D
(
x
N
)
]
\begin{equation} \Phi = \begin{bmatrix} \phi_0(x_1) & \phi_1(x_1) & \cdots & \phi_D(x_1) \\ \phi_0(x_2) & \phi_1(x_2) & \cdots & \phi_D(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(x_N) & \phi_1(x_N) & \cdots & \phi_D(x_N) \end{bmatrix} \end{equation}
Φ=
ϕ0(x1)ϕ0(x2)⋮ϕ0(xN)ϕ1(x1)ϕ1(x2)⋮ϕ1(xN)⋯⋯⋱⋯ϕD(x1)ϕD(x2)⋮ϕD(xN)
ϕ
(
x
n
)
T
=
{
ϕ
0
(
x
n
)
,
⋯
,
ϕ
D
(
x
n
)
}
\begin{equation} \phi(x_n)^T=\{\phi_0(x_n),\cdots,\phi_D(x_n)\} \end{equation}
ϕ(xn)T={ϕ0(xn),⋯,ϕD(xn)}
用矩阵的形式表示为:
w
=
(
Φ
T
Φ
)
−
1
Φ
T
t
\begin{equation} w=(\Phi^T\Phi)^{-1}\Phi^Tt \end{equation}
w=(ΦTΦ)−1ΦTt
其中
Φ
†
=
(
Φ
T
Φ
)
−
1
Φ
T
\Phi^{\dagger}=(\Phi^T\Phi)^{-1}\Phi^T
Φ†=(ΦTΦ)−1ΦT为伪逆矩阵
在
w
w
w中
w
0
w_0
w0是截距,我们此时可以将其拿出来讨论
E
D
(
w
)
=
1
2
∑
n
=
1
N
{
t
n
−
w
0
−
∑
j
=
1
D
w
j
ϕ
j
(
x
n
)
}
2
\begin{equation} E_D(w)=\frac{1}{2}\sum\limits_{n=1}^{N}\{t_n - w_0 - \sum\limits^{D}_{j=1}w_j\phi_j(x_n)\}^2 \end{equation}
ED(w)=21n=1∑N{tn−w0−j=1∑Dwjϕj(xn)}2
首先,我们对
w
0
w_0
w0 求偏导:
∂
E
D
(
w
)
∂
w
0
=
−
∑
n
=
1
N
{
t
n
−
w
0
−
∑
j
=
1
D
w
j
ϕ
j
(
x
n
)
}
\begin{equation} \frac{\partial E_D(w)}{\partial w_0} = -\sum_{n=1}^{N}\{t_n - w_0 - \sum_{j=1}^{D}w_j\phi_j(x_n)\} \end{equation}
∂w0∂ED(w)=−n=1∑N{tn−w0−j=1∑Dwjϕj(xn)}
然后,我们令该偏导数等于0,得到:
∑
n
=
1
N
{
t
n
−
w
0
−
∑
j
=
1
D
w
j
ϕ
j
(
x
n
)
}
=
0
\begin{equation} \sum_{n=1}^{N}\{t_n - w_0 - \sum_{j=1}^{D}w_j\phi_j(x_n)\} = 0 \end{equation}
n=1∑N{tn−w0−j=1∑Dwjϕj(xn)}=0
接着,我们可以将
w
0
w_0
w0 提出来,得到:
N
w
0
=
∑
n
=
1
N
t
n
−
∑
n
=
1
N
∑
j
=
1
D
w
j
ϕ
j
(
x
n
)
\begin{equation} Nw_0 = \sum_{n=1}^{N}t_n - \sum_{n=1}^{N}\sum_{j=1}^{D}w_j\phi_j(x_n) \end{equation}
Nw0=n=1∑Ntn−n=1∑Nj=1∑Dwjϕj(xn)
假设我们已经求出了
w
j
w_j
wj,
j
=
1
,
2
,
.
.
.
,
D
j = 1, 2, ..., D
j=1,2,...,D,那么
w
0
w_0
w0 的解为:
w
0
=
1
N
(
∑
n
=
1
N
t
n
−
∑
n
=
1
N
∑
j
=
1
D
w
j
ϕ
j
(
x
n
)
)
=
t
ˉ
−
∑
j
=
1
D
w
j
ϕ
j
‾
\begin{equation} \begin{align*} w_0 &= \frac{1}{N}\left(\sum_{n=1}^{N}t_n - \sum_{n=1}^{N}\sum_{j=1}^{D}w_j\phi_j(x_n)\right) \\ &=\bar{t} - \sum_{j=1}^{D}w_j\overline{\phi_j} \end{align*} \end{equation}
w0=N1(n=1∑Ntn−n=1∑Nj=1∑Dwjϕj(xn))=tˉ−j=1∑Dwjϕj
从此可以看出
w
0
w_0
w0就是目标值的平均值与训练集上基函数值的加权平均值之差
求解
β
\beta
β
对
β
\beta
β求导得:
−
N
2
β
−
1
2
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
n
)
}
2
\begin{equation} -\frac{N}{2\beta} -\frac{1}{2}\sum_{n=1}^{N}\{t_n - w^T\phi(x_n)\}^2 \end{equation}
−2βN−21n=1∑N{tn−wTϕ(xn)}2
令导数等于0,即得到:
β
−
1
=
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
n
)
}
2
N
\begin{equation} \beta^{-1} = \frac{\sum_{n=1}^{N}\{t_n - w^T\phi(x_n)\}^2}{N} \end{equation}
β−1=N∑n=1N{tn−wTϕ(xn)}2
由此可见
β
−
1
\beta^{-1}
β−1即为残差。
3.2 梯度下降法
当
X
X
X的数据量很大时,求
w
w
w的精确解中的
Φ
†
\Phi^{\dagger}
Φ†中的逆矩阵的复杂度太高,可能无法求解,使用梯度下降法可以求得
w
w
w的近似解。
w
t
+
1
=
w
t
−
η
∇
E
n
\begin{equation} w_{t+1} = w_{t}-\eta\nabla E_n \end{equation}
wt+1=wt−η∇En
∇
E
n
=
−
(
t
n
−
w
t
T
ϕ
(
x
n
)
)
ϕ
(
x
n
)
\begin{equation} \nabla E_n=-(t_n-w_t^T\phi(x_n))\phi(x_n) \end{equation}
∇En=−(tn−wtTϕ(xn))ϕ(xn)
3.3 正则化
3.3.1 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2正则化
我们通过最小化
E
D
(
w
)
+
λ
E
w
(
w
)
E_D(w)+\lambda E_w(w)
ED(w)+λEw(w)进行正则化求解参数
w
w
w
E
w
(
w
)
=
1
2
w
T
w
\begin{equation} E_w(w)=\frac{1}{2}w^Tw \end{equation}
Ew(w)=21wTw
w
w
w的精确解:对
w
w
w求导,并等于0得到:
∑
n
=
1
N
t
n
ϕ
(
x
n
)
T
−
∑
n
=
1
N
w
T
ϕ
(
x
n
)
ϕ
(
x
n
)
T
+
λ
w
=
0
\begin{equation} \sum_{n=1}^{N} t_n\phi(x_n)^T - \sum_{n=1}^{N} w^T\phi(x_n)\phi(x_n)^T + \lambda w= 0 \end{equation}
n=1∑Ntnϕ(xn)T−n=1∑NwTϕ(xn)ϕ(xn)T+λw=0
∑ n = 1 N t n ϕ ( x n ) T − w T ( ∑ n = 1 N ϕ ( x n ) ϕ ( x n ) T ) + λ w = 0 \begin{equation} \sum_{n=1}^{N} t_n\phi(x_n)^T - w^T\left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T\right) + \lambda w = 0 \end{equation} n=1∑Ntnϕ(xn)T−wT(n=1∑Nϕ(xn)ϕ(xn)T)+λw=0
w T ( ∑ n = 1 N ϕ ( x n ) ϕ ( x n ) T + λ I ) = ∑ n = 1 N t n ϕ ( x n ) T \begin{equation} w^T\left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T+\lambda I \right) = \sum_{n=1}^{N} t_n\phi(x_n)^T \end{equation} wT(n=1∑Nϕ(xn)ϕ(xn)T+λI)=n=1∑Ntnϕ(xn)T
w
=
(
∑
n
=
1
N
ϕ
(
x
n
)
ϕ
(
x
n
)
T
+
λ
I
)
−
1
∑
n
=
1
N
t
n
ϕ
(
x
n
)
\begin{equation} w = \left(\sum_{n=1}^{N}\phi(x_n)\phi(x_n)^T+\lambda I \right)^{-1} \sum_{n=1}^{N} t_n\phi(x_n) \end{equation}
w=(n=1∑Nϕ(xn)ϕ(xn)T+λI)−1n=1∑Ntnϕ(xn)
用矩阵的形式表示为:
w
=
(
Φ
T
Φ
+
λ
I
)
−
1
Φ
T
t
\begin{equation} w=(\Phi^T\Phi+\lambda I )^{-1}\Phi^Tt \end{equation}
w=(ΦTΦ+λI)−1ΦTt
梯度下降法
加入正则化后,
w
w
w使用梯度下降进行求解:
w
t
+
1
=
w
t
−
η
∇
E
n
−
λ
∇
E
w
\begin{equation} w_{t+1} = w_{t}-\eta\nabla E_n-\lambda \nabla E_w \end{equation}
wt+1=wt−η∇En−λ∇Ew
∇
E
n
=
−
(
t
n
−
w
t
T
ϕ
(
x
n
)
)
ϕ
(
x
n
)
\begin{equation} \nabla E_n=-(t_n-w_t^T\phi(x_n))\phi(x_n) \end{equation}
∇En=−(tn−wtTϕ(xn))ϕ(xn)
∇
E
w
(
w
)
=
w
t
\begin{equation} \nabla E_w(w)= w_t \end{equation}
∇Ew(w)=wt
w
t
+
1
=
w
t
+
η
(
t
n
−
w
t
T
ϕ
(
x
n
)
)
ϕ
(
x
n
)
−
λ
w
t
\begin{equation} w_{t+1} = w_{t} + \eta (t_n - w_t^T \phi(x_n)) \phi(x_n) - \lambda w_t \end{equation}
wt+1=wt+η(tn−wtTϕ(xn))ϕ(xn)−λwt
3.3.2 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣正则化
Lasso回归就是多元线性回归加上了 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣正则化,求解过程参考Lasso
代码实现
二、多项式回归
1、问题描述
多项式拟合是一种数学与统计学中常见的技术,主要用于通过一个多项式函数来近似描述一组数据点的分布趋势。它是回归分析的一种,也叫多项式拟合,是机器学习和数据分析中的重要工具。
这你我门只考虑一维的数据,具体来说,如果我们有一组数据点
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
n
,
y
n
)
}
D=\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}
D={(x1,y1),(x2,y2),…,(xn,yn)},我们可能想找到一个多项式函数
P
(
x
,
w
)
=
w
0
+
w
1
x
+
w
2
x
2
+
…
+
w
m
x
m
P(x,w) = w_0 + w_1x + w_2x^2 + \ldots + w_mx^m
P(x,w)=w0+w1x+w2x2+…+wmxm,使得该函数在这些点上的值与实际的
y
y
y 值尽可能接近。这就是多项式拟合的主要目标。
2、模型建模
多项式回归方程:
P
(
x
,
w
)
=
w
0
+
w
1
x
+
w
2
x
2
+
…
+
w
m
x
m
\begin{equation} P(x,w) = w_0 + w_1x + w_2x^2 + \ldots + w_mx^m \end{equation}
P(x,w)=w0+w1x+w2x2+…+wmxm
目标:最小化均方误差
E
D
(
w
)
E_D(w)
ED(w)
E
D
(
w
)
=
1
2
∑
n
=
1
N
{
P
(
x
n
,
w
)
−
t
n
}
2
\begin{equation} E_D(w)=\frac{1}{2} \sum\limits^{N}_{n=1}\{P(x_n,w)-t_n\}^2 \end{equation}
ED(w)=21n=1∑N{P(xn,w)−tn}2
3、模型求解
已知:数据集 x = { x 1 , x 2 , ⋯ , x N } , t = { t 1 , t 2 , ⋯ , t N } x=\{x_1,x_2,\cdots,x_N\},t=\{t_1,t_2,\cdots,t_N\} x={x1,x2,⋯,xN},t={t1,t2,⋯,tN},回归方程 P ( x , w ) = w 0 + w 1 x + w 2 x 2 + … + w m x m P(x,w) = w_0 + w_1x + w_2x^2 + \ldots + w_mx^m P(x,w)=w0+w1x+w2x2+…+wmxm,目标 w ∗ = arg min w E D ( w ) = arg min w 1 2 ∑ n = 1 N { P ( x n , w ) − t n } 2 w^* = \underset{w}{\argmin} E_D(w)= \underset{w}{\argmin}\frac{1}{2} \sum\limits^{N}_{n=1}\{P(x_n,w)-t_n\}^2 w∗=wargminED(w)=wargmin21n=1∑N{P(xn,w)−tn}2
3.1精确解
我们将模型的预测值带入
E
D
(
w
)
E_D(w)
ED(w)中:
E
D
(
w
)
=
1
2
∑
n
=
1
N
{
w
0
+
w
1
x
n
+
w
2
x
n
2
+
…
+
w
m
x
n
m
−
t
n
}
2
\begin{equation} E_D(w)=\frac{1}{2} \sum\limits^{N}_{n=1}\{ w_0 + w_1x_n + w_2x_n^2 + \ldots + w_mx_n^m-t_n\}^2 \end{equation}
ED(w)=21n=1∑N{w0+w1xn+w2xn2+…+wmxnm−tn}2
分别对w求导得到:
∂
E
D
(
w
)
∂
w
i
=
∑
n
=
1
N
x
n
i
(
w
0
+
w
1
x
n
+
w
2
x
n
2
+
…
+
w
m
x
n
m
−
t
n
)
\begin{equation} \frac{\partial E_D(w)}{\partial w_i} = \sum_{n=1}^{N} x_n^i (w_0 + w_1 x_n + w_2 x_n^2 + \ldots + w_m x_n^m - t_n) \end{equation}
∂wi∂ED(w)=n=1∑Nxni(w0+w1xn+w2xn2+…+wmxnm−tn)
一共有
m
+
1
m+1
m+1个方程和
m
+
1
m+1
m+1个参数,用矩阵或者消元法是可以求解的,但是我们定睛一看,如果我们把
x
n
=
[
1
,
x
n
,
x
n
2
,
…
,
x
n
m
]
T
\mathbf{x}_n = [1, x_n, x_n^2, \ldots, x_n^m]^T
xn=[1,xn,xn2,…,xnm]T看成多元线性回规中的
x
n
=
[
1
,
x
n
1
,
x
n
2
,
…
,
x
n
m
]
T
\mathbf{x}_n = [1, x_{n1}, x_{n2}, \ldots, x_{nm}]^T
xn=[1,xn1,xn2,…,xnm]T,
w
=
[
w
0
,
w
1
,
…
,
w
m
]
T
\mathbf{w} = [w_0, w_1, \ldots, w_m]^T
w=[w0,w1,…,wm]T仍然为多元线性回归中的
w
w
w,那么问题就变成了求解多元线性回归,那么
w
w
w的解就是
w
=
(
X
T
X
)
−
1
X
T
t
\mathbf{w} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{t}
w=(XTX)−1XTt,那么这里的
X
\mathbf{X}
X和
t
\mathbf{t}
t分别为
X
=
[
1
x
1
x
1
2
…
x
1
m
1
x
2
x
2
2
…
x
2
m
⋮
⋮
⋮
⋱
⋮
1
x
N
x
N
2
…
x
N
m
]
\begin{equation} \mathbf{X} = \begin{bmatrix} 1 & x_1 & x_1^2 & \ldots & x_1^m \\ 1 & x_2 & x_2^2 & \ldots & x_2^m \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_N & x_N^2 & \ldots & x_N^m \end{bmatrix} \end{equation}
X=
11⋮1x1x2⋮xNx12x22⋮xN2……⋱…x1mx2m⋮xNm
t
=
[
t
1
t
2
⋮
t
N
]
\begin{equation} \mathbf{t} = \begin{bmatrix} t_1 \\ t_2 \\ \vdots \\ t_N \end{bmatrix} \end{equation}
t=
t1t2⋮tN
在这里我们也可以直接使用矩阵的形式推导一下参数
w
\mathbf{w}
w的结果,那么
E
D
(
w
)
E_D(w)
ED(w)可以写成:
E
D
(
w
)
=
(
X
w
−
t
)
T
(
X
w
−
t
)
=
w
T
X
T
X
w
−
2
t
T
X
w
+
t
T
t
\begin{equation} \begin{align*} E_D(w)&=(\mathbf{X}\mathbf{w}-\mathbf{t})^T(\mathbf{X}\mathbf{w}-\mathbf{t}) \\ &= \mathbf{w}^T \mathbf{X}^T \mathbf{X} \mathbf{w} - 2 \mathbf{t}^T \mathbf{X} \mathbf{w} + \mathbf{t}^T \mathbf{t} \end{align*} \end{equation}
ED(w)=(Xw−t)T(Xw−t)=wTXTXw−2tTXw+tTt
然后,我们可以分别计算这三项关于
w
\mathbf{w}
w 的导数:
- 对于第一项 w T X T X w \mathbf{w}^T \mathbf{X}^T \mathbf{X} \mathbf{w} wTXTXw,我们可以将其看作是 w \mathbf{w} w 和 X T X w \mathbf{X}^T \mathbf{X} \mathbf{w} XTXw 的点积,它的导数为:
∂ ∂ w w T X T X w = 2 X T X w \begin{equation} \frac{\partial}{\partial \mathbf{w}} \mathbf{w}^T \mathbf{X}^T \mathbf{X} \mathbf{w} = 2 \mathbf{X}^T \mathbf{X} \mathbf{w} \end{equation} ∂w∂wTXTXw=2XTXw
- 对于第二项 − 2 t T X w -2 \mathbf{t}^T \mathbf{X} \mathbf{w} −2tTXw,它是 w \mathbf{w} w 的线性函数,它的导数为:
∂ ∂ w − 2 t T X w = − 2 X T t \begin{equation} \frac{\partial}{\partial \mathbf{w}} -2 \mathbf{t}^T \mathbf{X} \mathbf{w} = -2 \mathbf{X}^T \mathbf{t} \end{equation} ∂w∂−2tTXw=−2XTt
- 对于第三项 t T t \mathbf{t}^T \mathbf{t} tTt,它是常数,对 w \mathbf{w} w 的导数为0。
因此,误差函数 E D ( w ) E_D(w) ED(w) 关于 w \mathbf{w} w 的梯度为:
∇
E
D
(
w
)
=
2
X
T
X
w
−
2
X
T
t
\begin{equation} \nabla E_D(w) = 2 \mathbf{X}^T \mathbf{X} \mathbf{w} - 2 \mathbf{X}^T \mathbf{t} \end{equation}
∇ED(w)=2XTXw−2XTt
最后令
∇
E
D
(
w
)
=
0
\nabla E_D(w) =0
∇ED(w)=0即可以解得
w
=
(
X
T
X
)
−
1
X
T
t
\mathbf{w} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{t}
w=(XTX)−1XTt
3.2正则化
多项式拟合如果多项式的次数偏高,很容易过拟合,我们也可以通过正则化进行求解,其求解过程与多元线性回归相同。
E
D
(
w
)
=
(
X
w
−
t
)
T
(
X
w
−
t
)
\begin{equation} E_D(w)=(\mathbf{X}\mathbf{w}-\mathbf{t})^T(\mathbf{X}\mathbf{w}-\mathbf{t}) \end{equation}
ED(w)=(Xw−t)T(Xw−t)
E
w
(
w
)
=
1
2
w
T
w
\begin{equation} E_w(w)=\frac{1}{2}\mathbf{w}^T\mathbf{w} \end{equation}
Ew(w)=21wTw
w
=
(
X
T
X
+
λ
I
)
−
1
X
T
t
\begin{equation} \mathbf{w}=(\mathbf{X}^T\mathbf{X}+\lambda \mathbf{I})^{-1}\mathbf{X}^T\mathbf{t} \end{equation}
w=(XTX+λI)−1XTt
4、代码实现
三、Lasso回归
Lasso回归就是多元线性回归加上了
∣
∣
w
∣
∣
||w||
∣∣w∣∣正则化,在这里我们不再介绍其背景和建模部门,其求解过程在多元线性回归的基础加上了
L
1
L_1
L1正则化,即:
L
=
R
S
S
(
w
)
+
E
w
(
w
)
=
(
X
w
−
t
)
T
(
X
w
−
t
)
+
λ
∣
∣
w
∣
∣
1
=
∑
n
=
1
N
{
t
n
−
w
T
ϕ
(
x
n
)
}
2
+
λ
∣
∣
w
∣
∣
1
\begin{equation} \begin{align*} \mathcal{L} &= RSS(w)+E_w(w) \\ &= (Xw-t)^T(Xw-t)+\lambda||w||_1 \\ &=\sum\limits_{n=1}^{N}\{t_n-w^T\phi (x_n)\}^2+\lambda||w||_1 \end{align*} \end{equation}
L=RSS(w)+Ew(w)=(Xw−t)T(Xw−t)+λ∣∣w∣∣1=n=1∑N{tn−wTϕ(xn)}2+λ∣∣w∣∣1
如果这里用的 M S E MSE MSE代替 R S S RSS RSS最后的结果也会差一个系数 N N N,这里前面也会经常使用 E D ( w ) E_D(w) ED(w),会差一个系数2
1、模型求解
首先看
R
S
S
RSS
RSS部分
R
S
S
RSS
RSS对
w
j
w_j
wj进行求导得:
∇
R
S
S
=
−
2
∑
n
=
1
N
ϕ
j
(
x
n
)
{
t
n
−
w
T
ϕ
(
x
n
)
}
=
−
2
∑
n
=
1
N
ϕ
j
(
x
n
)
{
t
n
−
∑
k
=
1
m
w
k
ϕ
k
(
x
n
)
}
=
−
2
∑
n
=
1
N
ϕ
j
(
x
n
)
{
t
n
−
∑
k
=
1
,
j
≠
k
m
w
k
ϕ
k
(
x
n
)
−
w
j
ϕ
j
(
x
n
)
}
=
−
2
∑
n
=
1
N
ϕ
j
(
x
n
)
{
t
n
−
∑
k
=
1
,
j
≠
k
m
w
k
ϕ
k
(
x
n
)
}
+
2
∑
n
=
1
N
w
j
ϕ
j
(
x
n
)
2
}
=
−
2
ρ
j
+
2
w
j
z
j
\begin{equation} \begin{align*} \nabla RSS &= -2\sum\limits_{n=1}^{N}\phi_j (x_n)\{t_n-w^T\phi (x_n)\} \\ &= -2\sum\limits_{n=1}^{N}\phi_j (x_n)\{t_n- \sum\limits_{k=1}^{m}w_k\phi_k (x_n)\} \\ &= -2\sum\limits_{n=1}^{N}\phi_j (x_n)\{t_n- \sum\limits_{k=1,j\neq k}^{m}w_k\phi_k (x_n)- w_j\phi_j (x_n)\} \\ &= -2\sum\limits_{n=1}^{N}\phi_j (x_n)\{t_n- \sum\limits_{k=1,j\neq k}^{m}w_k\phi_k (x_n)\}+2 \sum\limits_{n=1}^{N} w_j\phi_j (x_n)^2\} \\ &= -2 \rho_j + 2w_jz_j \end{align*} \end{equation}
∇RSS=−2n=1∑Nϕj(xn){tn−wTϕ(xn)}=−2n=1∑Nϕj(xn){tn−k=1∑mwkϕk(xn)}=−2n=1∑Nϕj(xn){tn−k=1,j=k∑mwkϕk(xn)−wjϕj(xn)}=−2n=1∑Nϕj(xn){tn−k=1,j=k∑mwkϕk(xn)}+2n=1∑Nwjϕj(xn)2}=−2ρj+2wjzj
令
∇
R
S
S
=
0
\nabla RSS = 0
∇RSS=0得到
w
j
=
ρ
j
/
z
j
w_j=\rho_j/z_j
wj=ρj/zj
由于
L
1
L_1
L1是不可导的,我们这里使用
L
1
L_1
L1对
w
j
w_j
wj的次梯度,即:
∇
L
1
=
{
λ
,
w
j
>
0
[
−
λ
,
λ
]
,
w
j
=
0
−
λ
w
j
<
0
\begin{equation} \nabla L_1= \left\{ \begin{aligned} & \lambda, & w_j>0\\ & [-\lambda, \lambda], &w_j=0\\ & -\lambda & w_j<0 \end{aligned} \right. \end{equation}
∇L1=⎩
⎨
⎧λ,[−λ,λ],−λwj>0wj=0wj<0
将
∇
R
S
S
\nabla RSS
∇RSS和
∇
L
1
\nabla L_1
∇L1合起来:
∇
L
=
−
2
ρ
j
+
2
w
j
z
j
+
{
λ
,
w
j
>
0
[
−
λ
,
λ
]
,
w
j
=
0
−
λ
w
j
<
0
\begin{equation} \nabla \mathcal{L} = -2 \rho_j + 2w_jz_j+ \left\{ \begin{aligned} & \lambda, & w_j>0\\ & [-\lambda, \lambda], &w_j=0\\ & -\lambda & w_j<0 \end{aligned} \right. \end{equation}
∇L=−2ρj+2wjzj+⎩
⎨
⎧λ,[−λ,λ],−λwj>0wj=0wj<0
∇
L
=
{
−
2
ρ
j
+
2
w
j
z
j
+
λ
,
w
j
>
0
[
−
2
ρ
j
−
λ
,
−
2
ρ
j
+
λ
]
,
w
j
=
0
−
2
ρ
j
+
2
w
j
z
j
+
−
λ
w
j
<
0
\begin{equation} \nabla \mathcal{L} = \left\{ \begin{aligned} &-2 \rho_j + 2w_jz_j+ \lambda, & w_j>0\\ &[-2 \rho_j -\lambda, -2 \rho_j +\lambda], &w_j=0\\ &-2 \rho_j + 2w_jz_j+ -\lambda & w_j<0 \end{aligned} \right. \end{equation}
∇L=⎩
⎨
⎧−2ρj+2wjzj+λ,[−2ρj−λ,−2ρj+λ],−2ρj+2wjzj+−λwj>0wj=0wj<0
令
∇
L
=
0
\nabla \mathcal{L} = 0
∇L=0得到
w
j
w_j
wj
w
j
=
{
ρ
j
−
λ
/
2
z
j
,
w
j
>
0
0
,
w
j
=
0
ρ
j
+
λ
/
2
z
j
w
j
<
0
\begin{equation} w_j = \left\{ \begin{aligned} & \frac{\rho_j - \lambda/2}{z_j}, & w_j>0\\ &0, &w_j=0\\ & \frac{\rho_j + \lambda/2}{z_j}& w_j<0 \end{aligned} \right. \end{equation}
wj=⎩
⎨
⎧zjρj−λ/2,0,zjρj+λ/2wj>0wj=0wj<0
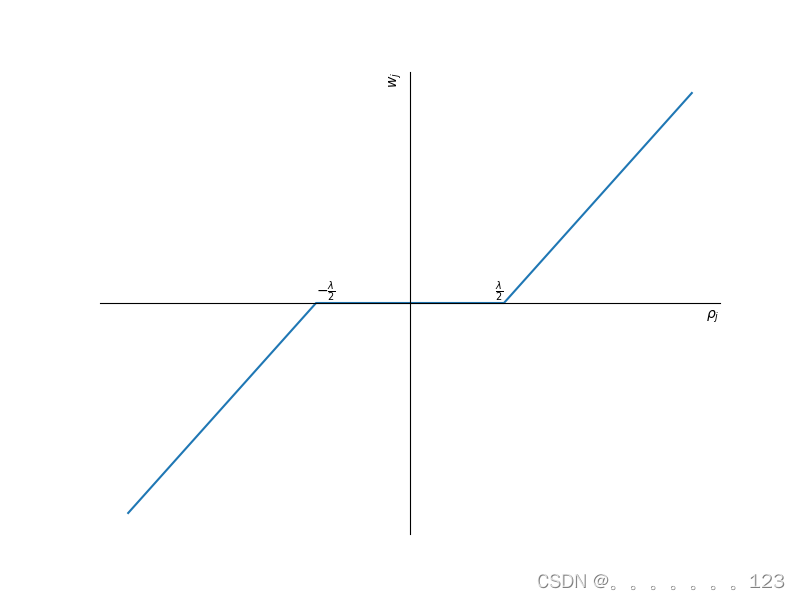
从上面的图可以看出,当
∣
ρ
j
∣
<
λ
2
|\rho_j|<\frac{\lambda}{2}
∣ρj∣<2λ时
w
j
w_j
wj会缩水为0,而如果只有
R
S
S
RSS
RSS做为损失的时候,只有
ρ
j
=
0
\rho_j=0
ρj=0时
w
j
w_j
wj才会为0,因此lasso回归求得参数相比于正常回归对参数进行了裁剪,并且有更多的机会等于0,参数也更为稀疏。
Lasso回归使用坐标下降法更新参数
w
w
w,通过求解上述
w
j
w_j
wj求解其中是的损失下降最大的进行更新,其他
w
k
w_k
wk保持不变,直到收敛。
正则化的几何解释
L
1
L_1
L1正则化也可以写成有约束的形式:
minimize
w
1
2
(
X
w
−
t
)
T
(
X
w
−
t
)
subject to
∣
∣
w
∣
∣
1
≤
ϵ
\begin{equation} \begin{aligned} &\underset{w}{\text{minimize}} & & \frac{1}{2}(Xw-t)^T(Xw-t) \\ &\text{subject to} & & ||w||_1 \leq \epsilon \end{aligned} \end{equation}
wminimizesubject to21(Xw−t)T(Xw−t)∣∣w∣∣1≤ϵ
假设
w
=
{
w
1
,
w
2
}
w=\{w_1,w_2\}
w={w1,w2}是一个二维的参数,那么我们可以在平面坐标上表示出
w
w
w的可行域与目标。
首先我们了解一下二次型图像的概念,目标函数是一个二次型
(
X
w
−
t
)
T
(
X
w
−
t
)
=
w
T
X
T
X
w
−
2
t
T
X
w
+
w
T
w
=
l
o
s
s
(Xw-t)^T(Xw-t)=w^TX^TXw-2t^TXw+w^Tw=loss
(Xw−t)T(Xw−t)=wTXTXw−2tTXw+wTw=loss,那么圆锥曲线3种可能:椭圆、抛物线、双曲线
- 如果 d e t ( X T X ) > 0 det(X^TX) > 0 det(XTX)>0,那么目标函数对应的是椭圆
- 如果
d
e
t
(
X
T
X
)
=
0
det(X^TX) = 0
det(XTX)=0,那么目标函数对应的是抛物线
如果数据 X X X的变量之间存在多重共线性,那么 d e t ( X T X ) = 0 det(X^TX)=0 det(XTX)=0,但是我们假设变量之间不存在多重共线性,所以目标函数是椭圆曲线,接着我们只要画出可行域,找到椭圆曲线与可行域的顶点相交或相切即为最优值。
我们将
L
1
L_1
L1范数进行变形:
∥
[
w
1
w
2
]
∥
=
∣
∣
w
1
∣
∣
+
∣
∣
w
2
∣
∣
≤
ϵ
\begin{equation} \left\| \begin{bmatrix} w_1 \\ w_2 \\ \end{bmatrix} \right\| = ||w_1||+||w_2|| \leq \epsilon \end{equation}
[w1w2]
=∣∣w1∣∣+∣∣w2∣∣≤ϵ
{
w
1
+
w
2
≤
ϵ
,
w
1
≥
0
,
w
2
≥
0
w
1
−
w
2
≤
ϵ
,
w
1
≥
0
,
w
2
<
0
−
w
1
+
w
2
≤
ϵ
,
w
1
<
0
,
w
2
≥
0
−
w
1
−
w
2
≤
ϵ
,
w
1
<
0
,
w
2
<
0
\begin{equation} \begin{cases} w_1 + w_2 \leq \epsilon, & w_1 \geq 0, w_2 \geq 0 \\ w_1 - w_2 \leq \epsilon, & w_1 \geq 0, w_2 < 0 \\ -w_1 + w_2 \leq \epsilon, & w_1 < 0, w_2 \geq 0 \\ -w_1 - w_2 \leq \epsilon, & w_1 < 0, w_2 < 0 \end{cases} \end{equation}
⎩
⎨
⎧w1+w2≤ϵ,w1−w2≤ϵ,−w1+w2≤ϵ,−w1−w2≤ϵ,w1≥0,w2≥0w1≥0,w2<0w1<0,w2≥0w1<0,w2<0
由此可见
L
1
L_1
L1范数的可行域是一个封闭的正方形,其顶点都落在坐标轴上。我们同样也可以画出1/2范数、2范数、4范数和无穷范数的可行域,那么可行域与目标曲线如下图所示:
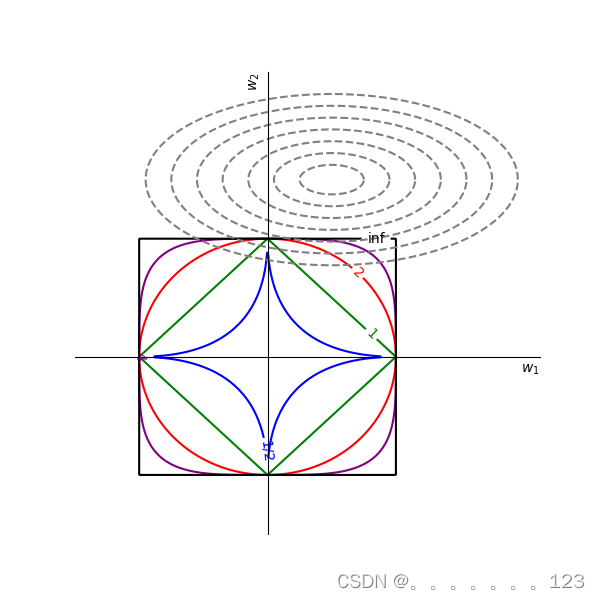
从图中可以发现,
L
1
L_1
L1范数更容易比
L
2
L_2
L2范数交于角点,这也更容易让
w
w
w取到等于0的值,从而解释了
L
1
L_1
L1范数得到的参数更为稀疏。
四、岭回归
岭回归
归就是多元线性回归加上了
∣
∣
w
∣
∣
2
||w||^2
∣∣w∣∣2正则化,求解过程参考第一张的3.3.1节
参考
- Bishop C M, Nasrabadi N M. Pattern recognition and machine learning[M]. New York: springer, 2006.






















 1479
1479











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








