GCD（莫比乌斯反演（数论公式+结论+因子个数）

这道题是真的好题！！！！我也是头一次搞莫比乌斯反演，没想到那么有用，但是的确对于它的理解是很有难度的！！！
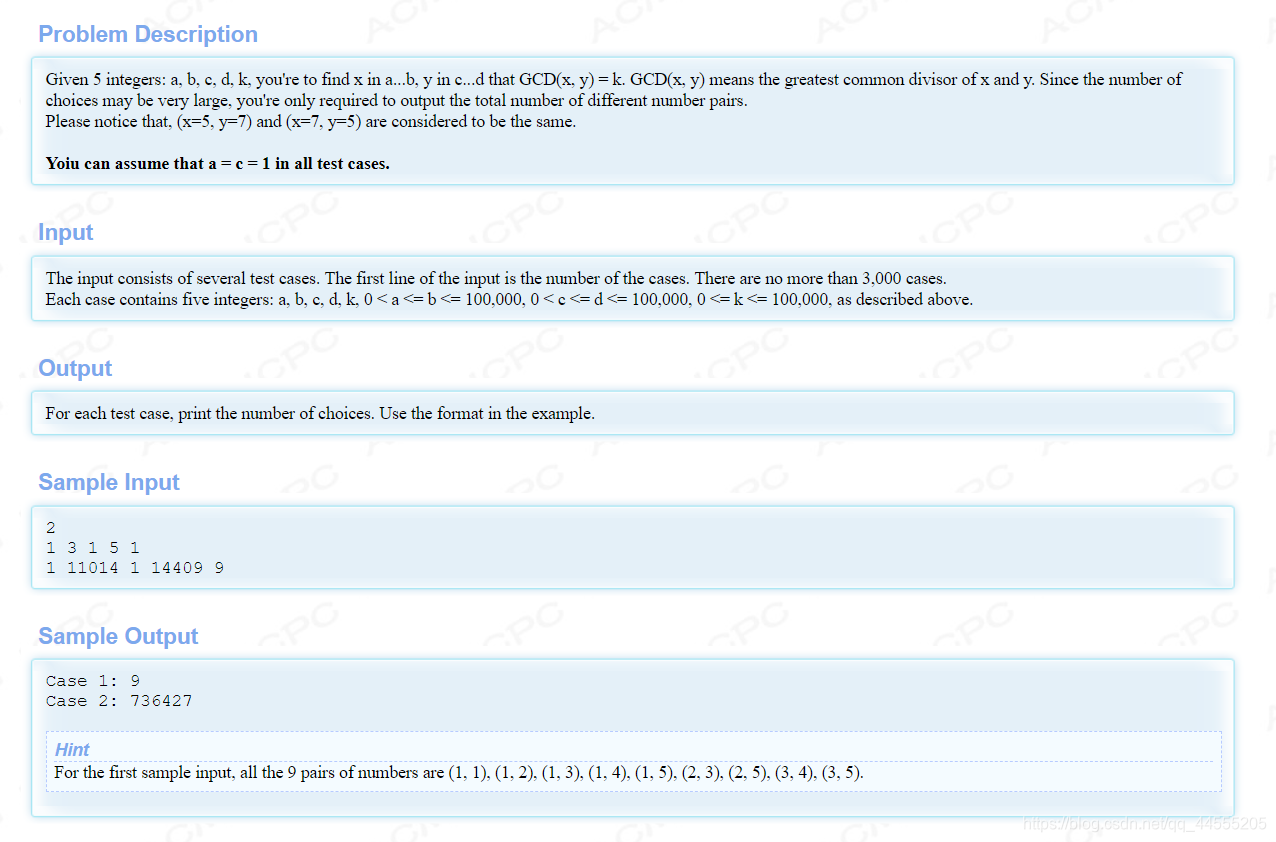
题的意思很简单就是求在[a,b]区间取出的x和[c,d]区间取出的y使得gcd(x,y)==k的对数（注意这里的x,y为无序的）并且题上说了把a=c=1；
当时我拿着这个题，一脸的懵逼，QAQ；
然后百度了一下说是莫比乌斯反演；那什么是莫比乌斯反演呢？
其实我感觉如果要去证明是很难看懂的；但是自己还是尽量去理解吧，嘻嘻；
其实莫比乌斯反演就是如果我能构造出一个公式：
然后构造出另一个公式：

那么使得这两个构造的公式有这样的关系：
那么我我就可以利用莫比乌斯反演来化简了；
但是怎么去构造呢？
就这个题而言我可以这样构造：
f(n)为gcd(x,y)==n的(x,y)的配对的个数；
F(n)为n|gcd(x,y)的(x,y)的配对的个数；
很显然，这道题就是求F(1)的(x,y)的配对的个数；
注意：上面的f(n)中的n和F(n)中的n不是同一个n；为了方便我写成:f(d)吧；
所以这样就可以知道能够整除n的(x,y)的对数肯定等于所有满足是n的倍数的(x,y)的配对个数的和；也就是n|d;如果对gcd很熟悉的可以很好理解；但是请注意这里算重了：为什么？比如在区间[1,2]选；那么按照上面的配对方式就有:

所以实际算出来的是左边这种，而我要想得到右边这种（因为题上说了(1,2)和(2,1)是认为相同的）；所以去重就[1,min(b,d)]中，只有这里面才算的两次，这样就可以理解为什么需要去重了；如果题上不说(x,y)和(y,x)相同的话，就不用去重了；
在这里需要知道这个结论：其实如果学过容斥定理（算集合整除的应该容易理解）：
就是gcd(x,y)==n的配对个等于(x/n)*(y/n);为什么呢？可以这样理解：比如gcd(4,2)2;那么配对个数就为2乘12；因为这里要用到高中的独立事件；因为[1,4]只有2,4两种情况，[1,2]中只有2一种情况，所以总得情况就是2种配对；
所以这个理解之后再来看莫比乌斯反演公式：

根据我前面定义的函数，直接带进来就可以了；然后令n=1就可以得到：

那么d的范围是多少呢？根据上面的函数定义我可以知道d的范围就是[1,min(b,d)];就这样咯；嘻嘻；
然后求u[d]的模板一带+容斥定理理解就AC了；
其实这道题考的东西挺多的；不光是莫比乌斯反演，还考察了gcd及[1,n]中能被n整除的个数常用的数论结论；我还是挺开心的，头一次搞明白莫比乌斯反演，虽然复杂，但是自己想想还是能理解的；

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100000;
int pri[N+5],mu[N+5],num;
bool ss[N+5];
void get_mu()//得到u系数的模板直接存在mu数组中从下标1开始 
{
    mu[1]=1;
    for (int i=2;i<=N;i++)
    {
        if (!ss[i]) 
        {
            pri[++num]=i;
            mu[i]=-1;
        }
        for (int j=1;pri[j]*i<=N && j<=num;j++)
        {
            ss[pri[j]*i]=1;
            if (i%pri[j]==0)
            {
                mu[pri[j]*i]=0;break;
            }
            mu[pri[j]*i]=-mu[i];
        }
    }
}
int main(){
	int T,g=0;
	get_mu();
	scanf("%d",&T);
	while(T--){
		 int a,b,c,d,k;
		 scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
		 printf("Case %d: ",++g);
		 if(k==0)puts("0");//因为题目说了a,c都是>=1的，所以如果k为0；那么根本不会存在（x,y） 
		 else{
		 	int up=min(b,d);//因为这里只需要枚举到最小的就OK了 
		 	b/=k;d/=k;//因为gcd(x,y)==k可以转化为gcd(x/k,y/k)==1,所以这里可以缩小范围 
		 	ll ans1=0;
		 	ll ans2=0;
		 	if(b>d)swap(b,d);//因为我只用小的一个 
		 //	cout<<b<<"  "<<d<<endl;
		 	for(int i=1;i<=up;i++){
		 		   ans1+=1ll*mu[i]*(b/i)*(d/i);
		 		   ans2+=1ll*mu[i]*(b/i)*(b/i);//容斥定理+数论算因子个数 
			 }
			 printf("%lld\n",ans1-ans2/2);
		 }
		 
	}
	return 0;
}