如何使用Excel拟合任意方程曲线？（包含求R2、方程未知数和绘制曲线图像的教程）

当你有自变量和因变量，还知道相应方程公式，如何仅利用Excel画出拟合曲线并得出相应准确方程？

1. 准备：

首先打开Excel加载项中的“规划求解”（文件-选项-加载项-分析工具库-转到-勾选“规划求解加载项”-确定）

以本人数据为例，构建一个类似的表格（蓝色部分先不管，右下角部分X和Y先不管，MS为我的分类，也可以不管，a和b后随便输入一个数即可）：

本表格中，第一列的[GSP]是所有已知的X，第二列的[ANPP]是所有已知的Y，在我的实验中本地ANPP与GSP应为指数相关关系，即Y=a*e^(bX)，因此yi=下面的表格中应输入“=$H$2*EXP($H$3*A2)”，然后双击单元格右下角小十字应用到整列。如果你有别的方程记得修改为对应的方程；

相应的，下面的表格中应输入“=(A2-C2)^2”，然后应用到整列；此时ymean后的H4单元格中应输入“=AVERAGE(C2:C142)”，注意本公式中“142”仅为本人数据量，记得改成自己的；

相应的，[(y-ymean)2]下面的表格中应输入“=(A2-$H$4)^2”，然后应用到整列。

[残差平方和（SSE）]后应输入“=SUM(E2:E142)“，注意本公式中“142”仅为本人数据量，记得改成自己的；

[总离差平方和（SST）]后应输入”=SUM(E2:E142)“，注意本公式中“142”仅为本人数据量，记得改成自己的；

后应输入”=1-(H6/H7)“。

至此准备工作结束。

2. 求解：

合适的方程应使[残差平方和（SSE）]最小，因此我们使用规划求解（数据-分析-规划求解），将设置目标修改为”$H$6“，到最小值，通过更改可变单元格设置为a和b，即”$H$2:$H$3“，然后点击”求解“，即可得到相应[残差平方和（SSE）]最小的a和b的值。

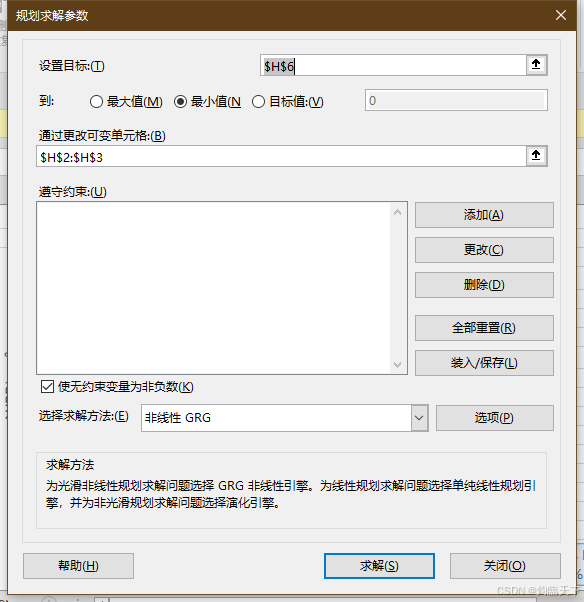
点击求解后确定即可：

本示例中得到得到a和b如下：

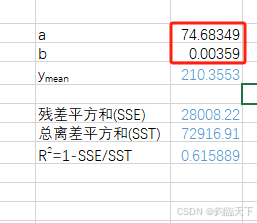
因而我们可知该方程应为：y = 74.683e^(0.0036x)。

3. 绘图：

3.1. 绘制数据散点图

以此我们来构建图像，先“插入-散点图”：

把相应的X和Y对应选上：

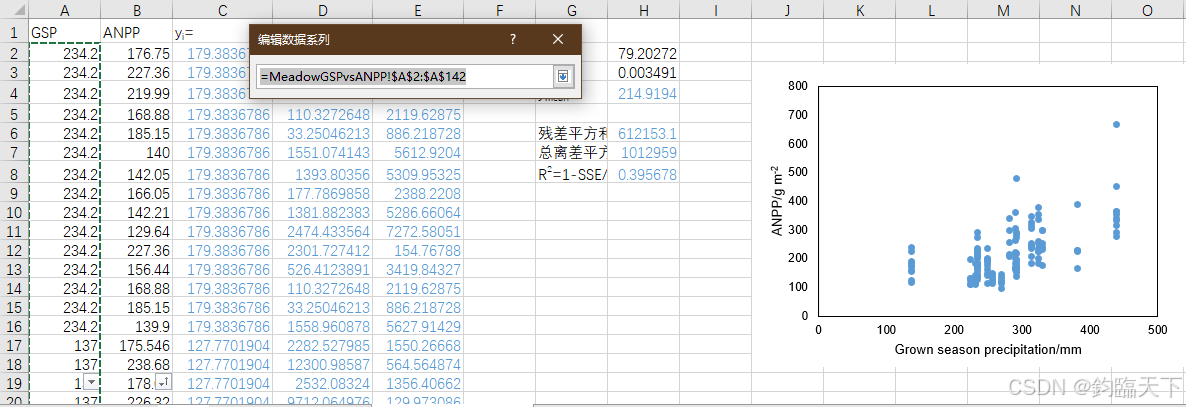
至此，所有数据的散点图得到了。

3.2 绘制拟合曲线

然后再画拟合曲线，首先构建一列X和Y，由于Y是由X计算得来的，就先把X复制过来，然后在Y列输入相应公式计算出Y的值：

然后把这两列数据选中，点击“数据-筛选”，然后点X后面的箭头选“升序”，所有数据便按照升序排列了。此时便可以添加为拟合曲线：先点击图片，然后屏幕最上方选“图表工具-设计-选择数据-添加”，把X和Y相应添加上，然后右键点击图片中添加上的点，选择“设置数据点格式”，右边增加的框选择“线条-实线”：

标记选择“数据标记选项-无”：

我们便得到了该散点图的拟合曲线：

最后添加文本框，把方程、和P值打上即可。