LeedCode＜简单＞ 69. x 的平方根【牛顿迭代、泰勒级数】

题目描述：

实现 int sqrt(int x) 函数（开方）。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

---

实现方式有很多种，

• 袖珍计算器算法：

核心思想：我们的目的是对给定的数字进行开方，既然不让我们直接用开方，我们可以将其进行转化，变着花样地使用开方。例如，我们在高中学过的，对一个数字 a，取 e 的 lna 次方，那么结果仍旧是 a。（不一定非要e，只要真数和底数相等就可以）即

• 二分查找：

这个方法不用多说，大家都知道，无限逼近。

• 牛顿迭代：

用这个方法来解决开方的问题其实并不难，尤其是数学不错的小伙伴，可以认真的学习一下这个方法，十分有趣。用到的核心思想是用切线来无限逼近零点，下面我们会仔细讲解这个方法。

1. 袖珍计算器算法

我们知道：

所以，我们就可以直接写代码了：

public static int mySqrt(int x) {
  if (x == 0){
    return 0;
  }

  int res = (int)Math.exp(0.5*Math.log(x));  // 使用int进行类型转化最终只保留整数部分

  return (res+1)*(res+1)==x?(res+1):res;
}

使用袖珍计算机有几个需要注意的点：

1. Math.log(x) 是取以 e 为底，x 的对数。Math 中暂时没有让我们可以选择任意数字作为底的方法。不过我们可以用 Math.log(m) / Math.log(n) 表示以 n 为底 m 的对数。
2. 不要忘记，这道题我们只需要保留真正开方结果的整数部分即可，不需要做四舍五入。
3. 还有一点十分重要！我们是先对 x 取以 e 为底的对数，这个过程因为产生的结果大多数情况都是小数，在做取舍时会产生一次误差，然后会再取 e 为底的指数。这个时候，因为底是 e，所以必然还要再产生一次误差。

看几个例子：

• Math.exp(0.5*Math.log(9))     --->   3.0000000000000004
• Math.exp(0.5*Math.log(16))   --->   4.0
• Math.exp(0.5*Math.log(25))   --->   4.999999999999999

可以很明显地看到，由于误差的存在，计算结果可能会偏大，也有可能会偏小，也有可能会刚刚好。所以我们在使用 floor 函数对计算结果进行处理时，一定要将这些不同的情况都考虑在内。方式很简单，只需要看被省略小数后的整数，其 +1 后进行平方，是否刚好等于我们要开方的数字即可。

2. 折半查找

折半查找很简单，就是通过求中间值，然后进行平方，和待开方数字做比较即可。使用的是 while 循环，退出条件是 r 跑到了 L 的左边，或者发现了 mid 平方之后和待开方数字相等的情况，上代码：

public static int mySqrt(int x) {
    if (x == 0){
        return 0;
    }else if (x == 2147483647){
        return 46340;
    }

    int l = 1, r = x, mid;

    while (l<=r){
        mid = (l+r)/2;
        if((long)mid*mid > x){
            r = mid-1;
        }else {
            if((long)mid*mid == x) {
                return mid;
            }
            l = mid+1;
        }
    }

    return r;
}

3. 牛顿迭代

这个方法只要理解了它的思想，其实并不难。

我们首先构建出来一个可以描述题干的函数：。C 是我们输入的要进行开方的数字。当 y=0 时，正解就是我们想要的结果。也就是，函数的零点为  ，即为 C 开方的结果。

首先，在曲线上，将 C 代入曲线得到点  ，这个点记为  ，在这个点做一条切线，切线和x轴有一个交点  。我们在曲线上找到水平坐标相同的点  。然后再过该点做切线，切线和x轴交点为  。以此类推下去，找到一个十分接近  的点即可。我们来一起分析一下如何用代码表示：

直线的斜率我们可以通过对曲线求导来获得，即 ，我们知道曲线上的点可以表示为：，结合这两点，就可以求出来切线的一般方程：

令 y = 0 ，可以很快地求出来切线的零点横坐标。上面公式中我们代入的是  这个点，我们可以把  看作当前的零点。那么，通过上面的式子， 令 y = 0 我们求出的就是下一个零点，我们记为 ，对式子进行整理，就得到了：

一定要注意，我们代入上一次计算的切线的零点横坐标 ，计算得到的下一个切线零点横坐标 ，只会无限逼近曲线零点 ，但是永远无法超过 。也就是说  可以视作上面公式无线趋近的一个点。

怎么理解呢？很简单，取值 C=9，前面说了，计算的结果只能无限逼近3，但是无法求得3。那我们直接代入一个极限值3，求得：

什么概念？我们代入 3，下次计算的结果仍然是 3，也就是说如果不加限制，那么在这里就陷入了一个死循环。我们根本就连 2.999999999999 都得不到，怎么可能让  跑到 3 的左边，对吧。

另外呢，这里我们构建的函数，并非一定要是 ， 也是可以的。不论哪一种，我们只需要按照步骤一步步求解即可。

判断十分接近  的方法有很多，举两个例子：

判断 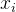 与 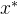  之间的距离，如果小于  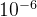，就可以认为它们非常接近了

代码很简单，我们一起来看一下：

public int mySqrt(int x) {

    if (x == 0){
        return 0;
    }

    double i=x;
    int m = 0;

    while (Math.abs(x-i*i) > 1e-6){
        i = (i + x/i) / 2;
    }

    return (int)i;
}

在距离判定条件  这里要注意了，这里最小只能写到  ，不能为了追求极致，把这个数字写的更小。

整个过程因为存在大量的小数，过程就必然会有取舍，因此势必会存在误差。当我们取的值是2147395599时，其中有一次的运算结果在做了舍入后， i = 46339.999989210184。巧妙的是，当我们将两者差的精度再提高到小于 。这个数字会再通过 i = (i+x/i)/2 运算一次，结果仍然为 46339.999989210184。然后，因为我们追求的精度太高了，于是就然后就陷入了死循环。

原因很简单，我们将 46339.999989210184 代入运算的结果，和 46339.999989210184 两者之间的差已经小于了 double 类型变量所能表示的小数位数，也就是小于了 ，舍入之后就直接被忽略了，因此就出现了死循环的局面。

举个例子，而我们将 46339.999989210184 带入 i = (i+x/i)/2 计算的真实结果可能是 46339.9999892101843009。但是由于小数只能保留12位，因此 3009 被忽略了，于是就出现了：将 46339.999989210184 代入计算的结果仍然是 46339.999989210184 的尴尬场景。因此死循环就出现了。

寻找 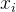 与  之间的距离小于 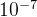 的时候

前面已经说了，我们每次求的  在无限逼近 ，那么只要两次求得的点  与  之间距离小于 ，我们就差不多可以认为到曲线的零点了。直接看代码：

class Solution {
    public int mySqrt(int x) {

        if (x == 0){
            return 0;
        }else if (x == 2147483647){
            return 46340;
        }

        double i2=x,i1=(x+1)/2;

        while (Math.abs(i2-i1)>1e-7){  // 寻找两个点之间的距离小于10^(-7)
            i2=i1;
            i1=0.5*(i2+x/i2);
        }

        return (int)i1;

    }
}

这个时候张三疑惑了，上面拿  与  做差的时候都不能小于 ，为什么这里能取  ？简单点说，就当参照物不同来理解吧，不然又得写一篇作文了。一个是拿动点与零点做参照，另一个是拿当前动点的前一个动点做参照。

 

---

到这里，三个主要的方法我们已经都分析完了。

不知道你有没有一个疑惑，预设的判断，有的只需要对 x 是否等于 0 进行判断，有的还多了一个对是否等于 2147483647 的判断。

我们先看一下多了这个判断的地方都有什么特点，就不让大家找了，我来告诉大家，只要需要这个判断，就说明下面必然有 x+1 这样的处理。

既然单独对它进行判断，那么它就一定是以一个特殊值，它是谁呢？它其实就是 int 的上限。

在计算机中保存的都是其对应的二进制的机器码。2147483647 对应的二进制数为：01111111 11111111 11111111 11111111，对这个数字加一，就变成了10000000 00000000 00000000 00000000。我们知道，首位为1表示负数。而一个负数的源码，等于其补码取反+1。刚好就等于了 int 类型的最小负数。

2147483647 是所能输入的最大值，所以只需要对它单独处理一下即可，不用考虑更大的数字。