Educational Codeforces Round 104 (Rated for Div. 2) C. Minimum Ties（思维+构造）

最新推荐文章于 2021-11-12 22:15:36 发布

原创最新推荐文章于 2021-11-12 22:15:36 发布 · 189 阅读

0 ·

CC 4.0 BY-SA版权

Codeforces 专栏收录该内容

80 篇文章

订阅专栏

这篇博客探讨了一种确保所有队伍得分相同的比赛计分构造方法，特别是当队伍数量为奇数和平数时如何最小化平局次数。对于奇数个队伍，可以通过交替输出1和-1实现；而对于偶数个队伍，需要构造特定的矩阵来达到目标，确保1和-1的数量相等，同时平局场次最少。作者反思了自己在解决这个问题时思维的灵活性不足。

传送门

题目大意

有 $n$ 个队伍，两两之间要进行一场比赛，一共进行 $\frac{n(n-1)}{2}$ 次比赛， $a, b$ 两队比赛的计分规则如下：

若两队伍平手输出 $0$ ，且两队均得一分。
若 $a$ 胜利则输出 $1$ ， $a$ 得3分 $b$ 不得分。
若 $b$ 胜利则输出 $- 1$ ， $b$ 得3分 $a$ 不得分。

给出一种构造方式使得所有队伍得分相同且平手的场次最少。

解题思路

首先通过打表若 $n$ 为奇数则直接 $1, - 1$ 交替输出即可，否则最少的平手场次是确定的，即 $\frac{n}{2}$ 场，然后可以发现有很多种构造方法，我们只需找到一种，这里的思路现场没写出来，实际上就是 $n * n$ 方阵的右上角部分凑够 $\frac{n}{2}$ 个0，然后使得1和-1个数相同即可。
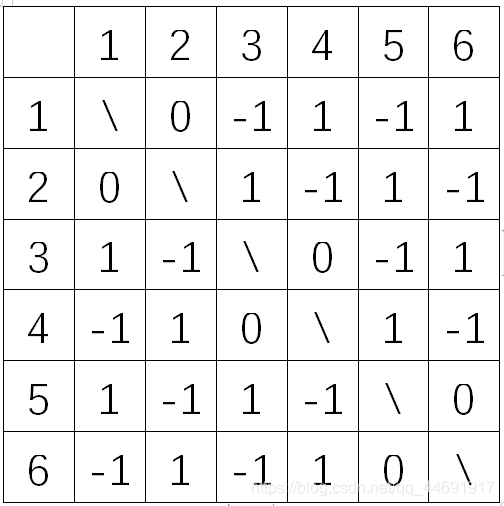
在这里插入图片描述
后来知道这个思路后很快就写出来了，还是思维不够灵活。

#include <bits/stdc++.h>

using namespace std;
#define ENDL "\n"

int a[105][105];

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t, n, k;
    cin >> t;
    while (t--) {
        cin >> n;
        if (n == 2) {
            cout << "0" << ENDL;
            continue;
        }
        int x = n * (n - 1) / 2;
        if (x % n == 0) {
            for (int i = 1; i <= x; i++) {
                if (i & 1) cout << "1 ";
                else cout << "-1 ";
            }
            cout << ENDL;
        } else {
            memset(a, -1, sizeof a);
            for (int i = 1; i <= n; i++) {
                if (i & 1) a[i][i + 1] = 0;
                else a[i][i + 1] = 1;
            }
            for (int i = n; i > 2; i -= 2) {
                int delta = i - 1;
                for (int j = 1; j + delta <= n; j++) {
                    a[j][j + delta] = 1;
                }
            }
            for (int i = 1; i <= n; i++) {
                for (int j = i + 1; j <= n; j++) {
                    cout << a[i][j] << " ";
                }
            }
            cout << ENDL;
        }
    }
    return 0;
}