计算 KL距离 (相对熵)

KL距离，是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（RelativeEntropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)的事件空间，若用概率分布Q（x）编码时，平均每个基本事件（符号）编码长度增加了多少比特。

我们用D（P||Q）表示KL距离，计算公式如下：

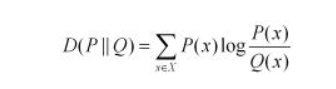
当两个概率分布完全相同时，即P(x)=Q(X)，其相对熵为0 。我们知道，概率分布P(X)的信息熵为：

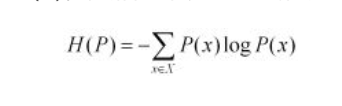
其表示，概率分布P(x)编码时，平均每个基本事件（符号）至少需要多少比特编码。通过信息熵的学习，我们知道不存在其他比按照本身概率分布更好的编码方式了，所以D(P||Q）始终大于等于0的。虽然KL被称为距离，但是其不满足距离定义的三个条件：1）非负性；2）对称性（不满足）；3）三角不等式（不满足）。

我们以一个例子来说明，KL距离的含义。

假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。现在通过观察，得到概率分布B与C。各个分布的具体情况如下：

A(0)=1/2，A(1)=1/2

B(0)=1/4，B(1)=3/4

C(0)=1/8，C(1)=7/8

那么，我们可以计算出得到如下：

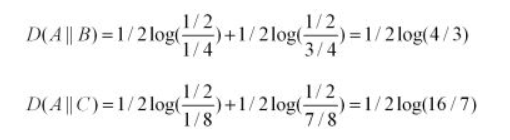
也即，这两种方式来进行编码，其结果都使得平均编码长度增加了。我们也可以看出，按照概率分布B进行编码，要比按照C进行编码，平均每个符号增加的比特数目少。从分布上也可以看出，实际上B要比C更接近实际分布。

如果实际分布为C，而我们用A分布来编码这个字符发射器的每个字符，那么同样我们可以得到如下：

再次，我们进一步验证了这样的结论：对一个信息源编码，按照其本身的概率分布进行编码，每个字符的平均比特数目最少。这就是信息熵的概念，衡量了信息源本身的不确定性。另外，可以看出KL距离不满足对称性，即D(P||Q)不一定等于D(Q||P)。

当然，我们也可以验证KL距离不满足三角不等式条件。

上面的三个概率分布，D(B||C)=1/4log2+3/4log(6/7)。可以得到：D(A||C) - (D(A||B)+ D(B||C)) =1/2log2+1/4log(7/6)>0，这里验证了KL距离不满足三角不等式条件。所以KL距离，并不是一种距离度量方式，虽然它有这样的学名。

其实，KL距离在信息检索领域，以及统计自然语言方面有重要的运用。

---

有个博主的理解

https://blog.csdn.net/qtlyx/article/details/51834684

KL散度又是一个从信息论、熵的角度考量距离的一个量。但是，这里说他是距离有点不妥，因为距离需要满足4个条件：

1. d(x,x) = 0 反身性
2. d(x,y) >= 0 非负性
3. d(x,y) = d(y,x) 对称性
4. d(x,k)+ d(k,y) >= d(x,y) 三角形法则

但是，很遗憾，我们的KL散度至满足前面两条，后面介绍的对称KL也只能满足前面三条。所以，我们叫KL散度，而不是叫KL距离。

如何直观的理解这样的一个度量的量呢。我不说什么用A的概率去编码B之类的，直观的去看KL散度的公式，说白了，P（x）部分可以认为是权重，其值就是P取该值的概率，后面的则是两者出现该变量的概率之比，然后取对数。取对数当然就是因为信息熵啦。也就是说，如果某一个变量出现的概率在P中很小，那么权重很小，即使在Q中很大，使得后半部分值比较大，那么最后值也不会很大；反过来也一样。所以，希望KL散度大，那么就需要有大的权重和大的概率差异，也就是，两个分布要不一样。

对称KL就是KL（P，Q）与KL（Q，P）的值加起来之后取平均。

---

python代码

import numpy as np
from scipy import *
def asymmetricKL(P,Q):
    return sum(P * log(P / Q)) #calculate the kl divergence between P and Q
 
def symmetricalKL(P,Q):
    return (asymmetricKL(P,Q)+asymmetricKL(Q,P))/2.00

---

https://blog.csdn.net/hfut_jf/article/details/71403741?tdsourcetag=s_pcqq_aiomsg

转载自hfut_jf

import numpy as np
import scipy.stats

# 随机生成两个离散型分布
x = [np.random.randint(1, 11) for i in range(10)]
print(x)
print(np.sum(x))
px = x / np.sum(x)
print(px)
y = [np.random.randint(1, 11) for i in range(10)]
print(y)
print(np.sum(y))
py = y / np.sum(y)
print(py)

# 利用scipy API进行计算
# scipy计算函数可以处理非归一化情况，因此这里使用
# scipy.stats.entropy(x, y)或scipy.stats.entropy(px, py)均可
KL = scipy.stats.entropy(x, y) 
print(KL)

# 编程实现
KL = 0.0
for i in range(10):
    KL += px[i] * np.log(px[i] / py[i])
    # print(str(px[i]) + ' ' + str(py[i]) + ' ' + str(px[i] * np.log(px[i] / py[i])))

print(KL)