循环冗余校验码
1、基本思想
循环冗余校验码的思想:
数据发送、接受方约定一个“除数”,K个信息位+R个校验位作为“被除数”,添加校验位后需保证二进制除法的余数为O。
收到数据后,进行除法检查余数是否为0。若余数非0说明出错,则进行重传或纠错

2、例:
设生成多项式为G(x)=x的3次方+x+的2次方+1,信息码为101001,求对应的CRC码。(讲解在3:15)
过程:
(1)通过生成多项式得到除数。
生成多项式可以写为1x的3次方+1x的2次方++0x的1次方1x的0次方,系数对应二进制数为1101
(2)检验位R=给定的生成多项式的最高次幂
k=信息码的长度=6,R=生成多项式的最高次幂=3,所以校验码位数=6+3=9
(3)确定校验位
信息码左移R位,低位补0。对移位后的信息码,用生成多项式进行模2除法,产生余数。
即101001000 模2除 1101

第一步,由于除数有4位,所以先取被除数的高4位,与除数商一次。模2除取商的方法为:只看当前被除数取出数的最高位,最高位为几,商为几。
第二步,进行模2减的运算(其实就是异或运算)。
第三步,被除数后边一位进行补充,再次进行这个过程。
所以,最后得到的对应的CRC码为 101001 001
(4)检错和纠错
发送: 101001001 记为C9C8C7C6C5C4C3C2C1
接收: 101001001 用1101进行模2除,余数为000,代表没有出错.
接收:101001011 用1101进行模2除,余数为010,代表C2出错(这句话的对错需要具体情况分析,由下表得可能是2,也可能是9)

只要我们确定了一个生成多项式,无论信息位怎么变化,最终余数的值和出错位对应是固定不变的。
此时,如果能满足2的R次方大于等于K+R+1,则CRC码可纠正一位错。

3、总结

二、定点数的表示
定点数:小数点的位置固定
1、分类

2、无符号数
无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。

n位的无符号数表示范围为:0 ~ 2的n次方 -1
3、有符号数
3.1、原码




用尾数表示真值的绝对值,符号位“0/1”对应“正/负”


3.2、反码
在原码基础上得到:
若符号位为0,则反码与原码相同
若符号位为1,则数值位全部取反
表示范围同原码
反码其实只是原码转变为补码的一个中间状态

3.3、补码
原码转变为反码,反码转变为补码。
正数的补码=原码
负数的补码=反码末位+1(要考虑进位)



3.4移码
补码的基础上将符号位取反。
注意:移码只能用于表示整数


4、运算
4.1、移位运算
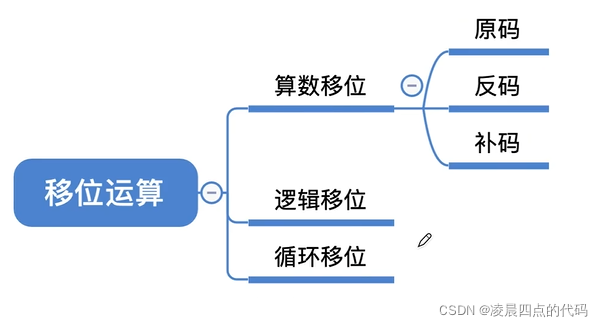
4.1.1算术移位
通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法
(1)原码的算数移位:符号位保持不变,仅对数值位进行移位。

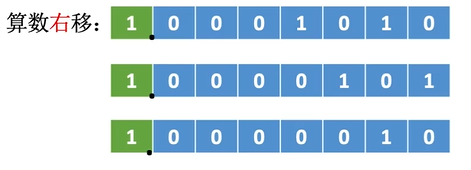
右移:高位补0,低位舍弃。若舍弃的位=0,则相当于÷2;若舍弃的位≠0,则会丢失精度
左移:低位补0,高位舍弃。若舍弃的位=0,则相当于×2;若舍弃的位≠O,则会出现严重误差
(2)反码的算数移位
反码的算数移位一正数的反码与原码相同,因此对正数反码的移位运算也和原码相同。
右移:高位补0,低位舍弃。
左移:低位补0,高位舍弃。
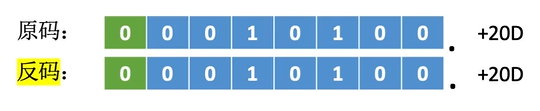
反码的算数移位――负教的反码数值位与原码相反,因此负数反码的移位运算规则如下,
右移:高位补1,低位舍弃。
左移:低位补1,高位舍弃。

(3)补码的算数移位
补码的算数移位――正数的补码与原码相同,因此对正数补码的移位运算也和原码相同。
补码的算数移位——负数补码=反码末位+1导致反码最右边几个连续的1都因进位而变为0,直到进位碰到第一个0为止。
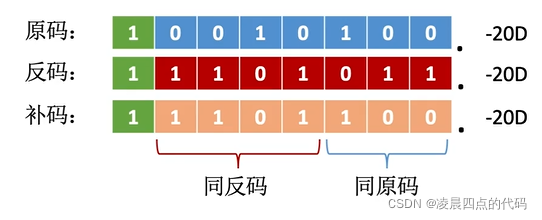
规律――负数补码中,最右边的1及其右边同原码。最右边的1的左边同反码
负数补码的算数移位规则如下:
右移(同反码):高位补1,低位舍弃
左移(同原码):低位补0,高位舍弃。
(4)总结

4.1.2逻辑移位
逻辑右移:高位补0,低位舍弃。
逻辑左移:低位补0,高位舍弃。
可以把逻辑移位看作是对“无符号数”的算数移位

4.1.3循环移位

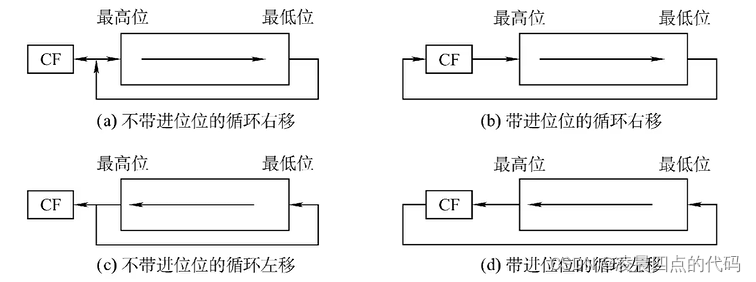
4.1.3总结

4.2、加减运算

4.2.1原码的加减运算:
(1)原码的加法运算:
正+正→绝对值做加法,结果为正
负+负→绝对值做加法,结果为负
(这两个可能会溢出)
正+负→绝对值大的减绝对值小的,符号同绝对值大的数
负+正→绝对值大的减绝对值小的,符号同绝对值大的数
(2)原码的减法运算,“减数”符号取反,转变为加法:
正-负→正+正
负-正→负+负
正-正→正+负
负-负→负+正
4.2.2补码的加减运算
对于补码来说,无论加法还是减法,最后都会转变成加法,由加法器实现运算,符号位也参与运算





4.2.3溢出判断
只有“正数+正数”才会上溢―正+正=负
只有“负数+负数”才会下溢―负+负=正
(1)方法一:采用一位符号位
设A的符号为As,B的符号为Bs,运算结果的符号为Ss,则溢出逻辑表达式为:

若V=0,表示无溢出;
若v=1,表示有溢出。
V用到的计算方法:
逻辑表达式
与:如ABC,表示A与B与C仅当A、B、C均为1时,ABC为1
A、B、C中有一个或多个为0,则ABC为0
或:如A+B+C,表示A或B或C
仅当A、B、C均为0时,A+B+C为0
A、B、C中有一个或多个为1,则A+B+C为1

(2)方法二:采用一位符号位,根据数据位进位情况判断溢出

Cs与C1不同时有溢出
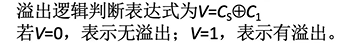
(3)方法三:采用双符号位
正数符号为00,负数符号为11

4.2.4符号扩展
定点整数的符号扩展:
在原符号位和数值位中间添加新位,正数都添0;负数原码添0,负数反、补码添1

定点小数的符号扩展:
在原符号位和数值位后面添加新位,正数都添0;负数原、补码添0,负数反码添1

4.2.5总结


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








