统计学第6天之一元线性回归

在下区区俗物

已于 2024-09-13 17:35:12 修改

阅读量781

点赞数 8

分类专栏：统计学基础文章标签：统计学

于 2024-09-08 10:48:00 首次发布

本文链接：https://blog.csdn.net/qq_44709053/article/details/141799924

版权

统计学基础专栏收录该内容

6 篇文章 0 订阅

订阅专栏

1、变量间关系的度量

函数关系

（1）是一一对应的确定关系；

（2）设有两个变量x和y，变量y随x一起变化，并完全依赖于x,当x取某个数值时，y根据确定的关系取相应的值，称y是x的函数，记为 $y=f(x)$ ,其中x称为自变量，y称为因变量；

（3）各观测点落在一条线上。

（4）函数关系的例子

某种商品的销售额y和销售量x之间的关系可以表示为 $y=px$ （p为单价）；
圆的面积S与半径之间的关系可以表示为 $S=\pi R^2$ ;
企业的原材料消耗额y与产量 $x_1$ 、单位产量消耗 $x_2$ 、原材料价格 $x_3$ 之间的关系可表示为： $y=x_1x_2x_3$

r的抽样分布

1、r的抽样分布随总体相关系数和样本容量的大小而变化

当样本数据来自正态总体时，随着n的增大，r的抽样分布趋于正态分布，尤其是在总体相关系数ρ很小或接近0时，区域正态分布的趋势非常明显。当ρ远离0时，除非n非常大，否则r的抽样分布呈现一定的偏态。

2、当为较大的正值时，r呈现左偏分布；当为较小的负值，r呈现右偏分布。只有当接近于0，而样本容量很大时，才能认为r是接近于正态分布的随机变量。

检验的步骤

1、检验两个变量之间是否存在线性相关关系;

2、采用费尔希提出的t检验，可以用于大样本，也可以用于小样本；

3、检验的步骤为

第一步：提出假设

$H _0:\rho=0,H_1:\rho \neq0$

第二步：计算p值

$t = |r| \sqrt{\frac{n-2}{1-r^2}} \sim t(n-2)$

第三步：确定显著性水平α，并做出决策

若 $|t|>t_{\alpha/2}$ ，表明总体的两个变量之间存在显著的线性关系

若 $| t |<t_{\alpha/2}$ ，不能拒绝原假设H0

对之前案例中的不良贷款与贷款余额之间的相关系数进行显著性检验（ $\alpha=0.05$ ）

解：第一步：提出假设

$H_0:\rho=0,H_1:\rho \neq 0$

第二步：计算检验的统计量

$t = |0.8436| \sqrt{\frac{25-2}{1-0.8436^2}} = 7.5344$

第三步：做出决策

根据显著性水平 $\alpha = 0.05$ ,查 t 分布表得 $t_{\alpha/2}(n-2)=2.069$

由于 $|t| = 7.5344>t_{\alpha/2}(n-2)=2.069$ ,拒绝H0，不良贷款与贷款余额之间存在显著性的正线性相关关系。

2、一元线性回归

回归分析，对于因变量Y，根据自变量X结合统计学模型（数学公式），预测出因变量Y。

（1）回归分析和相关性分析的区别

1、回归分析中，变量x和变量y处于平等的地位；回归分析中，y称为因变量，处于被解释的位置，x是自变量，用于预测因变量的变化。

2、相关分析中所涉及的变量x和y都是随机变量；回归分析中，因变量y是随机变量，自变量x可以是随机变量，也可以是非随机变量的确定变量。

3、相关性分析主要是描述两个变量之间线性关系的密切程度；回归分析不仅可以揭示自变量x对因变量y的影响大小，还可以由回归方程进行预测。

（2）一元线性回归模型

1、描述因变量y依赖自变量x和误差项的方程称为回归模型。

2、一元线性回归模型可以表示为：

$y = \beta_0+\beta_1 x+ \epsilon$

其中y是x的线性部分加上误差项，线性部分反映x的变化而引起y的变化，误差项反映的是除了线性关系之外的因素对y的影响，不能由x和y之间的线性关系揭示的变异性， $\beta_0,\beta_1$ 称为模型参数。

（3）基本假定

误差项 $\epsilon$ 是一个期望值为0的随机变量，对于一个给定的x，y的期望值为 $E(x)=\beta_1x+\beta_0$ ;

对于所有的x值， $\epsilon$ 的方差 $\sigma^2$ 都相同；

误差项 $\epsilon$ 是一个服从正态分布的随机变量，且相互独立。即 $\epsilon \sim N(0,\sigma^2)$ ;

独立性意味着对一个特定的x值，它所对应的 $\epsilon$ 与其他x对应的 $\epsilon$ 不相关；

对于一个特定的X值，它所对应的Y值与其他X所对应的Y值也不相关。

从上图可以看出，y的值随着x的不同而变化，但不论x怎么变化， $\epsilon$ 和y的概率分布是正态分布，并且具有相同的方差。

（4）回归方程

1、描述y的平均值或期望值如何依赖于x的方程称为回归方程；

2、一元线性回归方程的形式如下：

$y = \beta_0+\beta_1 x$

方程的图示是一条直线，也称为直线回归方程

$\beta_0$ 是回归直线在y轴上的截距，是当x=0时y的期望值

$\beta_1$ 是直线的斜率，称为回归系数，表示当x每变动一个单位时，y的平均变动值。

参数的最小二乘估计

作用是估计回归方程中 $\beta_0,\beta_1$ 的值。

1、使因变量的观察值与估计值之间的离差平方和达到最小来求 $\hat{\beta_0},\hat{\beta_1}$ 的方法。即

$\sum_{i=1}^{n}(y_i-\hat{y})^2=\sum_{i=1}^{n}(\hat{y}-\hat{\beta_0}-\hat{\beta_1}x_i)^2=$ 最小

2、用最小二乘法拟合的直线来代表x和y之间的关系与实际数据的误差比其他任何直线都小。

根据最小二乘法的要求，可以求解 $\hat{\beta_0},\ \hat{\beta_1}$ 的公式如下：

$\hat{\beta_1} = \frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=1}^{n}(X_i-\bar{X})^2}$

上述案例中不良贷款与各项贷款余额之间的回归方程

3、利用回归方程进行估计和预测

变差

1、因变量y的取值是不同的，y取值的这种波动性称为变差。变差来源于两个方面：

由于自变量x的取值不同造成的

除了x以为的其他因素（x对y的非线性影响，测量误差等）的影响。

2、对一个具体的观测值来说，变差的大小可以通过该实际观测值与其均值之差 $y-\bar y$ 表示

误差平方和的分解

1、总平方和（SST）：反映因变量n个值观察值与其均值的总误差；

2、回归平方和（SSR）：反映自变量X的变化对因变量Y取值变化的影响，即由于x和y之间的线性关系引起的取值变化，也成为可解释的平方和；

3、残差平方和：反映除X以为的其他因素对Y取值的影响，也成为不可解释的平方和或剩余平方和。

判定系数R方

1、回归平方和占总方差平方和的比例

2、反映回归直线的拟合程度；

3、取值范围在[0,1]之间；

4、 $R^2-->1$ 说明回归方程拟合的越好； $R_2-->0$ 说明回归方程拟合的越差；

5、判定系数等于相关系数的平方，即 $R^2=r^2$ 。

计算上述案例中不良贷款对单款余额回归的判定系数，并解释其意义。

判定系数的实际意义是：在不良贷款取值的变差中，有71.16%可以由不良贷款与贷款余额之间的线性关系来解释，或者说，在不良贷款的取值的变动中，有71.16%是由贷款余额所决定的。也就是说，不良贷款取值的差异2/3以上是由贷款余额决定的。可见不良贷款与贷款余额之间有较强的线性相关性。

估计标准误差

1、实际观察值与回归估计值离差平方和的均方根；

2、反映实际观察值在回归直线周围的分散状况；

3、对误差项 $\epsilon$ 的标准差 $\sigma$ 的估计，是在排除x对y的线性影响后，y随机波动大小的一个估计量；

4、反映用估计的回归方程预测y时预测误差的大小；

5、计算公式为

根据上述案例的计算结果，计算不良贷款对余额回归的估计标准误差，并解释其意义

实际上，Excel计算表中直接给出了该值，即标准误差为1.979948，根据贷款余额来估计不良贷款时，平均的估计误差为1.979948亿元。

显著性检验

回归分析的主要目的是根据所建立的估计方程，用自变量x来预测因变量y的取值。

建立估计方程后，不能立马使用其去预测，因为该估计方程是通过样本数据得出的方程，是否置信需要通过验证来证实。

回归分析中的显著性检验主要包含两个方面内容：一是线性关系的检验；二是回归系数的检验。

概念

1、检验自变量与因变量之间的线性关系是否显著；

2、将回归均方（MSR）同残差均方（MSE）加以比较，用用F检验来分析二者之间的差别是否显著：

回归均方MSR：回归均方和SSR除以相应的自由度（SSR的自由度是自变量的个数k，一元线性回归中自由度为1）
残差均方MSE：残差平方和SSE除以相应的自由度（SSE的自由度n-k-1，一元线性回归中自由度为n-2）

线性关系的检验

1.提出假设： $H_0:\beta_1=0$ 两个变量之间的线性关系不显著；

2.计算检验统计量 $F=\frac{SSR/1}{SSE/(n-2)} = \frac{MSR}{MSE} \sim F(1,n-2)$

3.作出决策：确定显著性水平 $\alpha$ ，并根据分子自由度1和分母自由度n-2找出临界值 $F_{\alpha}$ ，若 $F>F_{\alpha}$ 拒绝 $H_0$ ；若 $F<F_{\alpha}$ 不拒绝 $H_0$ 。

回归系数检验

概念

1.检验x和y之间是否具有线性关系，或者说，检验自变量x对因变量y的影响是否显著；

2.理论基础是回归系数 $\hat{\beta_1}$ 的抽样分布；

3.在一元线性回归中，等价于线性关系的显著性检验。

样本统计量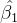 $\hat{\beta_1}$ 的分布

1. $\hat{\beta_1}$ 是分局最小二乘法求出的样本统计量，它有自己的分布；

2. $\hat{\beta_1}$ 分布具有如下性质：

分布形式：正态分布
数学期望： $E(\hat{\beta_1}) = \beta_1$

检验步骤

1、提出假设

$H_0:\beta_1=0$ 没有线性关系

$H_1;\beta_1 \neq 0$ 有线性关系

2、计算检验的统计量

3、确定显著性水平 $\alpha$ ,进行决策

在实际应用中，可以直接利用Excel输出的参数估计表进行检验。表中给出了用于检验的P值（P-value）。检验时可以直接将P- value与给定的显著性水平 $\alpha$ 。进行比较。在本例中，P-value=0.000<0.05,所以拒绝 $H_0$ 。

利用回归方程进行估计和预测

概念

1.根据自变量X的取值估计或预测因变量Y的取值；

2.估计和预测的类型；

点估计
- Y平均值的点估计
- Y个别值的点估计
区间估计
- Y平均值的区间估计
- Y的个别值的区间估计

点估计

1.对于自变量X的一个给定值 $x_0$ ，根据回归方程得到因变量y的一个估计值 $y_0$ ;

2.点估计值：平均值和个别值的点估计；

3.在点估计条件下，平均值的点估计和个别值的点估计是一样的，在区间估计中则不同。

Y的平均值的点估计

利用估计的回归方程，对于自变量x的一个给定值 $x_0$ ,求出因变量y的平均值的一个估计值 $E(y_0)$ ,就是平均值的点估计。

在前面的例子中，假如我们要估计贷款余额为100亿时，所有分行不良贷款的平均值，就是平均值的点估计。根据估计的回归方程得

区间估计

概念

1、利用估计的回归方程，对于自变量x的一个给定 $x_0$ ,求出因变量y的一个个别值的估计区间，这一区间成为预测区间。

2、 $y_0$ 在 $1-\alpha$ 置信水平下的预测区间为

影响区间宽度的因素

1.置信水平（ $1-\alpha$ ）:区间宽度随置信水平的增大而增大；

2.数据的离散程度S：区间宽度随离散程度的增大而增大；

3.样本容量：区间宽度样本容量的增大而减小；

4.用于预测的 $x_p$ 与 $\bar x$ 的差异程度：差异程度越大区间宽度越大

4、残差分析

残差与残差图

在回归模型 $y = \beta_0+\beta_1 x+ \epsilon$ 中，假定 $\epsilon$ 是期望为0，方差相等且服从正态分布的一个随机变量。如果关于 $\epsilon$ 的假定不成立，那么所做的检验以及估计和预测也许就站不住脚，确定 $\epsilon$ 的假定是否成立的方法之一就是进行残差分析。