1.题目分析
1.1问题描述
运行最大公约数的常用算法,并进行程序的调式与测试,要求程序设计风格良好,添加异常处理模块。
1.2分析过程
运行四种常用的计算最大公约数的算法,分别是辗转相除法、穷举法、更相减损法、Stein算法。在一个程序中分别调用四种方法,观察运行结果是否一致,添加异常处理模块,排除非法输入。
2.算法构造
2.1 辗转相除法
2.1.1求最大公约数
算法:
前提、定义两个数a和b,a做被除数,b做除数,temp为余数;
第一步:将较大的数放在a中,较小的放在b中;
第二步:求a/b的余数temp;
第三步:temp==0,返回b,b即为最大公约数;
第四步:temp!=0,将b的值赋给a,temp的值赋给b;
第五步:返回第二步操作;
流程图:

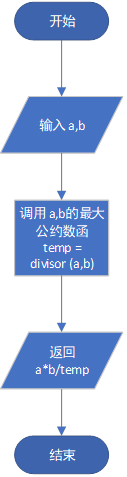
2.1.2求最小公倍数
算法:
第一步:定义两个数a和b
第二步:调用a,b的最大公约数函数;
第三步:返回结果,最小公倍数=a*b/最大公约数;
流程图:
2.2 穷举法
2.2.1求最大公约数
算法:
第一步:定义两个数a和b;
第二步:找到两个数中较小的数;
第三步:从较小数开始向1递减列举,知道找到最大公约 数停止;
流程图:

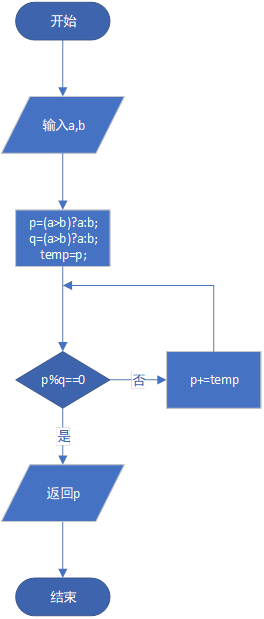
2.2.2 求最小公倍数
算法:
第一步:定义两个数a和b;
第二步:将较大的数记为p,较小的数记为q;
第三步:计算p/q的值
第四步:如果p/q==0则结束,返回p值;
第五步:如果p/q!=0,p自身相加,返回到第三步;
流程图:
2.3 更相减损法
2.3.1 求最大公约数
算法:
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;用i记录约简的次数,若不是则执行第二步;
第二步:以较大的数减较小的数,直到所得差值和较小数相等,记录这时的差为m;
第三步:返回pow(2,i)*m ,即为两个数的最大公约数。
流程图:

2.4 Stein算法
2.4.1 求最大公约数
算法:
第一步:定义两个数x和y;
第二步:若x和y都是偶数,则记录下公约数2,然后右移一位(即 除2)
第三步:若其中一个偶数一个基数,则偶数除2,此时2不可能是这 两个数的公约数了;
第四步:若两个都是基数,则x=|x-y|,y=min(x,y),若是x,y的公约数, 那么也是x-y和min(x,y)的公约数。
流程图:

3.算法实现
#include <iostream>
#include<math.h>
#include <Windows.h>
#include <time.h>
#define MAX 100000
//辗转相除法 嵌套调用
int divisor1 (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义整型变量*/
if(a<b) /*通过比较求出两个数中的最大值和最小值*/
{ temp=a;a=b;b=temp;} /*设置中间变量进行两数交换*/
while(b!=0) /*通过循环求两数的余数,直到余数为0*/
{
temp=a%b;
a=b; /*变量数值交换*/
b=temp;
}
return (a); /*返回最大公约数到调用函数处*/
}
int multiple1 (int a,int b) /*自定义函数求两数的最小公倍数*/
{
int divisor1 (int a,int b); /*自定义函数返回值类型*/
int temp;
temp=divisor1(a,b); /*再次调用自定义函数,求出最大公约数*/
return (a*b/temp); /*返回最小公倍数到主调函数处进行输出*/
}
//穷举法
int divisor2 (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义义整型变量*/
temp=(a>b)?b:a; /*采种条件运算表达式求出两个数中的最小值*/
while(temp>0)
{
if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除,则中止循环*/
break;
temp--; /*如不满足if条件则变量自减,直到能被a,b所整除*/
}
return (temp); /*返回满足条件的数到主调函数处*/
}
int multiple2 (int a,int b)
{
int p,q,temp;
p=(a>b)?a:b; /*求两个数中的最大值*/
q=(a>b)?b:a; /*求两个数中的最小值*/
temp=p; /*最大值赋给p为变量自增作准备*/
while(1) /*利用循环语句来求满足条件的数值*/
{
if(p%q==0)
break; /*只要找到变量的和数能被a或b所整除,则中止循环*/
p+=temp; /*如果条件不满足则变量自身相加*/
}
return (p);
}
//更相减损法
int gcd1(int m,int n)
{
int i=0,temp,x;
while(m%2==0 && n%2==0) //判断m和n能被多少个2整除
{
m/=2;
n/=2;
i+=1;
}
while(m!=n)
{
if(m>n)
m=m-n;
else
n=n-m;
}
return (pow(2,i)*m);
}
//Stein算法函数递归调用
int Stein( unsigned int x, unsigned int y) /* return the greatest common divisor of x and y */
{
int factor = 0;
int temp;
if ( x < y )
{
temp = x;
x = y;
y = temp;
}
if ( 0 == y )
{
return 0;
}
while ( x != y )
{
if ( x & 0x1 )
{ /* when x is odd */
if ( y & 0x1 )
{ /* when x and y are both odd */
y = ( x - y ) >> 1;
x -= y;
}
else
{ /* when x is odd and y is even */
y >>= 1;
}
}
else
{ /* when x is even */
if ( y & 0x1 )
{ /* when x is even and y is odd */
x >>= 1;
if ( x < y )
{
temp = x;
x = y;
y = temp;
}
}
else
{ /* when x and y are both even */
x >>= 1;
y >>= 1;
++factor;
}
}
}
return ( x << factor );
}
int main(void)
{
int m,n,t1,t2;
printf("Please input two integer numbers:");
scanf("%d%d",&m,&n);
if(m<0||n<0) //对非法输入的处理
{
printf("请重新输入数字:");
scanf("%d%d",&m,&n);
}
t1=divisor1(m,n); //调用辗转相除法函数求最大公约数
t2=multiple1(m,n); //调用辗转相除法函数求最小公倍数
printf("辗转相除法的函数嵌套调用结果:\n");
printf("The higest common divisor is %d\n",t1);
printf("The least common multiple is %d\n",t2);
t1=divisor2(m,n); //调用穷举法函数求最大公约数
t2=multiple2(m,n); //调用穷举法函数求最小公倍数
printf("穷举法的结果:\n");
printf("The higest common divisor is %d\n",t1);
printf("The least common multiple is %d\n",t2);
t1=gcd1(m,n); //调用更相减损法函数求最大公约数
printf("更相减损法的结果:\n");
printf("The highest common divisor is %d\n",t1);
t1=Stein(m,n); //调用stein算法函数求最大公约数
printf("stein算法的递归调用的结果:\n");
printf("The highest common divisor is %d\n",t1);
return 0;
}
4.调试、测试及运行结果
4.1程序调试结果及截图
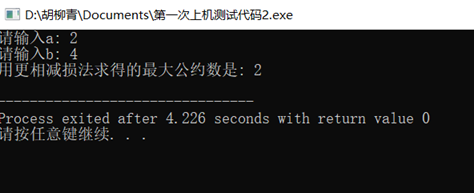
在程序调试阶段,我有两次更改,第一次程序运行时更相减损法所求公约数如果在输入的两个数是倍数关系是运行结果就会出错,如下图所示,正确结果应该是2,但是程序运行结果是1;
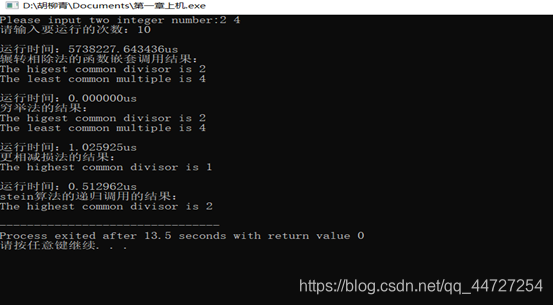
对这个问题,我将代码进行了修改,将如1所示的代码修改为了如2所示的代码。
1、while(x)
{
x=m-n;
m=(n>x)?n:x;
n=(n<x)?n:x;
if(n==(m-n))
break;
}
if(i==0)
return n;
else
return (int )pow(2,i)*n;
2、while(m!=n)
{
if(m>n)
m=m-n;
else
n=n-m;
}
return (pow(2,i)*m);
第二次是计算程序运行时间,刚开始用clock函数计算时间,它的时间精度确定到毫秒,所以在100组以下的时间太短,不能明确观察;改正后把时间精度精确到了微妙,可以更直观的观察四个函数对不同数据规模的运行时间,更方便比较。
4.2程序测试结果及截图
在程序测试阶段,我对四种算法运行出的结果正确性用测试代码进行了求证,并且比较了四种算法在不同数据规模下的运行时间。


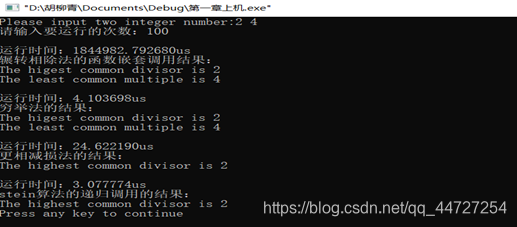
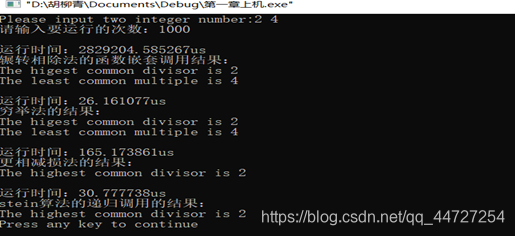

以上五张图分别是程序循环调用四个函数1次、10次、100次1000次、10000次时的运行时间,可以发现辗转相除法所用时间最多;其他三种算法所用时间差别不大,经过比较,可以得出结论:Stein算法、穷举法和更相减损法这三种算法在10组以内求公约数,穷举最优、Stein算法次之、更相减损法最慢;在10到10000组中求最大公约数,Stein算法最快、穷举法次之、更相减损法最慢;10000组以上,没有经过验证。
测试结果截图如下:


测试时间代码如下
#include <Windows.h>
#include <time.h>
#define MAX 100000
double run_time,dqFreq; //dqFreq是计时器频率
long x;
_LARGE_INTEGER time_start; //开始时间
_LARGE_INTEGER time_over; //结束时间
LARGE_INTEGER f; //计时器频率
QueryPerformanceFrequency(&f);
dqFreq=(double)f.QuadPart;
QueryPerformanceCounter(&time_start);
插入所要计算时间的函数
QueryPerformanceCounter(&time_over); //计时结束
run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;//乘以1000000把单位由秒化为微秒,精度为1000 000/(cpu主频)微秒
printf("\n运行时间:%fus\n",run_time);
5.经验归纳
这次的题目是比较四种算法求最大公约数,程序需要把这些模块整合到一起,我在更相减损法那一部分遇到了问题,每次运行这一块的结果都会出现问题,最后经过和同学讨论、上网查询之后修改了程序,解决了这个问题;在计算运行时间时,我开始用clock函数来计算,所得时间是负的,后来发现是开始和结束的位置没加对,改正之后在循环100组以内,所得时间多数为0,不能达到比较时间的目的,将时间精度由毫秒改为微秒之后,时间对比非常明显,达到了预期的效果。通过这次上机我学会了使用计算时间的两种函数,对于这次的程序我觉得还可以再做改进,可以将循环调用函数以达到计算多次运行所需时间的方法改成运用随机函数产生随机数组,这样可以使结论具有普遍性,排除了偶然性;还可以改变一下主函数,可以在主函数用switch语句分别调用四个函数,这样就可以在运行时自主选择你想要的方式。以上就是我对这次上机的总结归纳。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








