【paper】四旋翼编队防撞防死锁：双模型预测控制 + 事件触发

Dual Model Predictive Control of Multiple Quadrotors With Formation Maintenance and Collision Avoidance
2024.3
IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS 【Q1 7.7】
Wang Sifei 湖南大学

Q1 Background：本文试图解决一个什么样的问题？

本文开发了一种双模型预测控制方法，采用控制 Lyapunov 函数 (CLF) 和控制屏障函数 (CBF) 来支持没有领导者的多四旋翼系统中的编队和避碰，并用事件触发条件解决了CBF方法存在的死锁问题。

• 让四旋翼飞行器相互对飞，以检验所提方法是否能够消除死锁。
  

Q2 What’s Known：之前解决这个问题有哪些方法？

• 编队：
  • 基于一致性的算法（过于简单，需要额外的算法来实现防撞）、强化学习算法（过于复杂，需收集四旋翼飞行器群的数据，不能保证始终满足安全约束）和基于MPC 的编队控制方法 。 [11] 多旋翼利用一致性理论和受鸽子启发的避障行为来导航障碍物。[12]带有随机制动的改进深度强化学习方法，实现自动和灵活的编队调整。
  • MPC编队： [13] 基于协同进化算法的 MPC，与传统的基于粒子群优化的 MPC 相比，显著提高了编队控制性能。 [14] 基于神经动态优化的非线性 MPC 实现了领导者-跟随者移动机器人编队。 [15] 分布式 MPC 受编队约束的机器人的跟踪参考轨迹。
  • 😈MPC稳定性保证：[16] 控制 Lyapunov 函数 (CLF) 作为 MPC 的约束 。 [17] 自适应 CLF-MPC 用于不完整建模的四足机器人。在编队控制中，使用 CLF 的 MPC 应用有限。
• 防撞
  • 控制屏障函数 (CBF)。与已使用了 30 多年的人工势场 (APF) [18] 相比，CBF 在避障方面更有效、更稳健。 [19] 基于 NMPC-CBF 的方法来避开多面体之间的障碍物。解决死锁、非保守避障和动态可行性。[20] 预测 CBF 方法来创建预测安全过滤器。确保基于学习的控制方法的安全性。 [21] 使用 CLF-CBF 作为二次规划的约束构建了一个优化控制器。该控制器的设计同时满足安全条件和性能指标。
  • 😈CBF死锁： [8] 如果陷入死锁，可以引入干扰。[7] 检测到发生死锁时切换到旋转控制律。

Q3 What’s New：本文是用什么样的方法如何解决这个问题的？

• 本文提出了一种双层 MPC 控制器。上层【MPC-CLF】 + 下层【MPC-CBF】
  • 【MPC-CLF】实现队形收敛，生成标称输入
  • 【MPC-CBF】过滤 MPC-CLF 控制器提供的标称输入以实现避障。设计了一种事件触发机制来检测死锁的发生

预备知识

扩展类 K∞ 函数

一个连续函数 $\kappa :(-\infty ,\infty )\to \mathbb{R}$ 如果它满足以下条件，则称为 扩展类 K∞ 函数

1. 严格递增：$\kappa$ 是严格单调递增的，即 ${\kappa }^{\prime }(r)>0$。
2. 零点条件：$\kappa (0)=0$。
3. 无穷大条件：${\lim }_{r\to \infty }\kappa (r)=\infty$ 和 ${\lim }_{r\to -\infty }\kappa (r)=-\infty$。

• 这个函数有点类似于一个 “激励” 函数，用来描述系统状态如何远离或接近某个目标状态。扩展类 $K_{\infty }$ 函数是一个既能增长到无穷大也能下降到负无穷的函数，这意味着它可以表示系统的远离目标状态（当输入或状态很大时），同时也能在目标附近表现出适当的收敛（当输入或状态接近零时）。它的递增性质使得系统的动态能够随着状态的变化而变化，并且随着状态越来越远离目标，函数值会增大。

CLF (控制 Lyapunov 函数)

一个连续可微的函数 $V:{\mathbb{R}}^n\to \mathbb{R}$ ，如果存在扩展类 $K_{\infty }$ 函数 ${\kappa }_1,{\kappa }_2,{\kappa }_3$ 使得对于所有 $x\in {\mathbb{R}}^n$，都满足以下条件，则被称为 控制 Lyapunov 函数 (CLF)

1. ${\kappa }_1(|x|)\le V(x)\le {\kappa }_2(|x|)$，即 $V(x)$ 被两个扩展类 $K_{\infty }$ 函数包围。表示函数 $V(x)$ 随着状态的增大而增大，同时限制了它的增长速度
2. $\dot{V}(x)\le {\kappa }_3(|x|)$，即 $V(x)$ 的导数满足某种限制，表明系统的状态不会无限增加，也不会“跑得太快”。

• CLF 是一个用于分析系统稳定性的工具，确保系统状态从初始值收敛到目标状态。。它通过某个函数 $V(x)$ 来衡量系统状态距离目标状态（通常是原点或某个期望状态）的远近。

CBF (控制 barrier 函数)

考虑一个安全集 $H:=x|h(x)\ge 0\subset {\mathbb{R}}^n$，一个连续可微的函数 $h:{\mathbb{R}}^n\to \mathbb{R}$ 如果存在扩展类 $K_{\infty }$ 函数 $\kappa$ 使得满足以下条件，则被称为 控制 barrier 函数 (CBF)，

其中，$\dot{h}(x,u)$ 表示 $h(x)$ 对时间的导数，通常是系统动力学函数与控制输入 $u$ 的组合。

• CBF 用于描述系统的安全性，确保系统状态始终保持在安全集 $H$ 内。安全集 $H$ 是由函数 $h(x)$ 定义的，当 $h(x)\ge 0$ 时，系统状态被认为是安全的。
• 条件 $\dot{h}(x,u)+\kappa (h(x))\ge 0$ 确保在每一时刻，系统的状态不会越过安全边界，且通过合适的控制输入可以保持系统安全。扩展类 $K_{\infty }$ 函数 $\kappa$ 在这里的作用是约束控制输入，使得当系统接近安全边界时，控制输入可以调整系统的状态，防止其进入不安全区域。

问题建模

四旋翼

• 东北地 (NED)
  
  位置 pi ∈ R3 、线速度 νi ∈ R3
  旋转 Ri ∈ SO(3) 、沿 z 轴的单位向量 e3、质量 mi ∈ R
  角速度 ωi ∈ R3 、(·)∧ 为斜对称矩阵算子
  惯性矩阵 Ji ∈ R3×3 、推力 fi ∈ R 、 扭矩 τ i ∈ R3
• 简化成质点：这里的desc可以学习一下
  

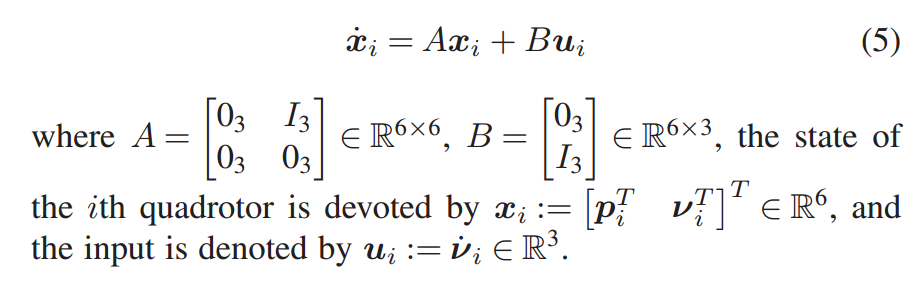
目标

需要有两个假设来确保编队控制的可控性。
🤖假设1：有向通信拓扑图保持连通。
🤖假设2：通过四旋翼之间的通信可以完全了解四旋翼的状态。
👉队形目标：假设第i个和第j个四旋翼之间的通信始终连通，则它们之间的期望相对位置为${\delta }_{ij}\in R^3$。则编队跟踪误差表示为$||p_i-p_j-{\delta }_{ij}||$。

👉安全目标：对于第i个四旋翼飞行器，它需要绕过周围环境中的静态障碍物以及群体中的其他四旋翼飞行器。表示安全性的函数称为 $h_i(x_i)$。当 $h_i(x_i)\ge 0$ 时，第 i 个四旋翼飞行器与障碍物和其他四旋翼飞行器处于安全距离，小于0表示不安全

具体方法

MPC-CLF：控制编队、速度一致性

• 第 i 个四旋翼飞行器的队形标称状态（由通信的四旋翼飞行器共同确定）

  • ${\alpha }_{ij}=1$表示第 i 个四旋翼飞行器到第 j 个四旋翼飞行器通信
  • ${\Delta }_{ij}$是第 i 个四旋翼飞行器与第 j 个四旋翼飞行器之间的编队
    
  • 导数
    

• 误差状态
  

• 优化问题
  

  • Lyapunov函数导数
    

• 引理1：当$J_{CLF}$等于0时，表示CLF的约束是松弛（slack）的

MPC - CBF：避碰

• 安全集：障碍物$P_b$，安全距离$d_{safe}$。
  
  
  👉通常，四旋翼飞行器的安全仅考虑基于位置的碰撞。因此安全集 Hi 仅限制位置的三个空间维度。然而，四旋翼飞行器的实际速度变化率由加速度决定，因此安全集也必须考虑速度。高阶 CBF 约束表示为：
  

• 屏障函数：
  
  👉高阶
  

• 沿状态轨迹的导数：
  

• 最优问题
  

• 引理2：当$J_{CBF}$等于0时，表示CBF的约束是松弛（slack）的

死锁检测与解决

• 定义死锁：如果第 i 个四旋翼飞行器保持静止（实际输入 $uˇi=0$ 且速度 $\nu i=0$），而标称控制输入 $uˆi$ ≠ 0，则该四旋翼飞行器陷入死锁
• 事件触发函数：
  
• 触发时机：假设死锁已经占据，事件触发函数Fi<0时，事件将被触发。
  
• 解决死锁的方法：在事件触发后调整标称状态$xˆi$
  
  

整体流程

Q4 What’s the Contribution：本文贡献

• 编队：MPC 通过将 CLF 作为约束来形成编队。这种方法依赖于邻居的状态，从而消除了对领导者的需求，而其他方案通常需要领导者。之前对四旋翼编队控制的 MPC-CLF 的研究有限。
• 避障：带有 CBF 的 MPC 是为避障而开发的。 MPC-CBF 过滤来自 MPCCLF 控制器的标称输入，以安全地实现避障。
• 解决碰撞死锁：事件触发机制旨在检测死锁的存在。 在发生死锁的有限时间邻域中，该机制只会触发一次，并且不会发生Zeno行为
• 真机实验

Q5 What’s the Inspiration：个人的启发，Creation和畅想

• 这个期刊接收挺快
• 首次见引入CBF在MPC中
• 整体问题偏简单，没有探讨期望编队是如何生成的
• 两个引理存在的意义是什么没太理解

可以做的点：

• 死锁可以作为一个点：这里解决死锁的关键就是修改标称状态，让下一时刻解出来的u部位0
• 可以弱化两个假设，本文未考虑扰动；
• 可以考虑一下这种双层的模式，通过CBF做避障，区别于之前的代价函数中引入软约束。
• 实验设备可以类似表二的参数列出来；