目录
动态规划法（Dynamic Programming）（第53题，第62题，第96题，第152题⭐，第221题，第300题，剑指第46题）
动态规划法的进阶——背包问题（322题，416题，494题）
双指针法(674题，第11题，第5题，第15题，第19题，第26题）
DFS（深度优先算法） 岛屿问题（463题,200 题）图像渲染问题（第733题）
回溯法的应用：DFS与全排列 （第46题，第47题，第17题，第22题）
机器人运动范围——数位之和(个位，十位，百位...之和)（剑指 13题）
😈😈二叉树展开为链表（第114题） 对二叉树遍历算法的进一步深化
二叉树的最大深度——带返回值递归函数和无返回值递归函数之间的转换（第104题）
😈反转链表（第206题 重点🐱🚀对于指针赋值操作的书写锻炼）
写在前面
引用知乎大佬的话什么是动态规划（Dynamic Programming）？动态规划的意义是什么？ - 知乎
计算机的本质是一个状态机，内存里存储的所有数据构成了当前的状态，CPU只能利用当前的状态计算出下一个状态（不要纠结硬盘之类的外部存储，就算考虑他们也只是扩大了状态的存储容量而已，并不能改变下一个状态只能从当前状态计算出来这一条铁律）
当你企图使用计算机解决一个问题是，其实就是在思考如何将这个问题表达成状态（用哪些变量存储哪些数据）以及如何在状态中转移（怎样根据一些变量计算出另一些变量）。所以所谓的空间复杂度就是为了支持你的计算所必需存储的状态最多有多少，所谓时间复杂度就是从初始状态到达最终状态中间需要多少步！
所以在我看来，刷题的过程其实就是如何借助使用者的智慧，用事先具有工作量的算法和数据结构来简化计算机的运算，让计算机对于问题具有一定的感性和适应性，而不只是暴力求解👴👴🏻。
时间复杂度和空间复杂度
O(1)：即是最低的时空复杂度。耗时/耗空间与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变。是常数级别的，并不是仅仅是1，可以是任何不随数据变化的常数
例：哈希算法，无论数据规模多大，都可以在一次计算后找到目标（不考虑冲突的话）
O(n)：时间复杂度为O(n)，就代表数据量增大几倍，耗时也增大几倍
例：遍历算法，找数组里最大或最小的值，需要把数组的 n 元素遍历一次，操作 n 次
O(n^2)：时间复杂度O(n^2)，就代表数据量增大n倍时，耗时增大n的平方倍
例：冒泡排序，双重for循坏，对n个数排序，需要扫描n×n次
O(log n)：当数据增大n倍时，耗时增大log n倍（这里的log是以2为底的，比如，当数据增大256倍时，耗时只增大8倍）
例：二分查找，每找一次排除一半的可能，256个数据中查找只要找8次就可以找到目标
O(n log n)：O(n log n)同理，就是n乘以log n，当数据增大256倍时，耗时增大256*8=2048倍
例：归并排序
应掌(会)握(背)的算法
快排、归并排、计数排、桶排、堆排、插排、冒泡、优先队列topK、手写hashMap、LRU、前缀树、最长回文串、最长上升子序列（两种dp）、子集、排列组合（二叉树和for循环俩版本都得会写）、非递归遍历二叉树、递归层序遍历。
哈希表（第一题）
一般用map来构造哈希表，一个关键字对应一个值
上题目：
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
示例 1：输入：nums = [2,7,11,15], target = 9
输出：[0,1]解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
此题为求两数之和的题目，因为要返回和等于target的两个数的下标，所以用map存储，关键字为nums[i],对应得值为i。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int len = nums.size();
map<int, int> mp;
vector<int> vec(2,0);
for(int i = 0; i < len; i++){
int other = target - nums[i];
if(mp.count(other) > 0 && mp[other] != i//避免某个数值是target的一半){
vec[0] = mp[other];
vec[1] = i;
break;
}
mp[nums[i]] = i;
}
return vec;
}
};哈希表进阶（第697题）
形如unordered_map<int, vector<int> > map
给定一个非空且只包含非负数的整数数组 nums，数组的度的定义是指数组里任一元素出现频数的最大值。你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组，返回其长度。
输入：[1, 2, 2, 3, 1] 输出：2
解释：
输入数组的度是2，因为元素1和2的出现频数最大，均为2.
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组[2, 2]的长度为2，所以返回2.输入：[1,2,2,3,1,4,2] 输出：6
class Solution {
public:
int findShortestSubArray(vector<int>& nums) {
int times = 0;
int len = 0;
unordered_map<int, vector<int> > map;
for (int i = 0; i < nums.size(); i++) {
if(map.count(nums[i])!=1)
map[nums[i]] = { 1,i,i };
else {
map[nums[i]][2] = i;
map[nums[i]][0]++;
}
}
for(auto it=map.begin();it!=map.end();it++){
if (it->second[0] > times||(it->second[0] ==times&&
(it->second[2] - it->second[1]) < len)) {
times = it->second[0];
len = (it->second[2] - it->second[1]);
}
}
return len+1;
}
};二分法 (35题,⭐287题，154题)
二分法准确的说应该叫二分查找法，适用于有序数组，它其实是一种跳跃式取数字索引下标值的方法。用二分法解题时，重点应该关注数组索引值的变化趋势，不能对边界值钻牛角尖，套用已有的一般二分法while循环可以大大简化过程。
在使用二分法时，最重要的是明确退出while循环的条件，即退出时，high，low，mid三个值之间的关系。
二分法对区间的划分有两种,如下：
第一种将区间分成了三块，这种算法一般用来查找某个target值在数组nums[]中的具体位置：
如果target在nums[]中存在，会返回具体的下标值；如果不存在，会返回-1。
如果我们要找的元素性质非常明确、并且简单，通常这样写就可以
while(low<=high)｛
mid=(low+high)/2;
if(target<nums[mid])
high=mid-1;
else if(target>nums[mid])
low=mid+1;
else
return mid;
｝
return -1;
/*当low+high时循环还会运行一次，所以退出时low=high=mid，也就是说这个
while（）循环结束时会返回target在数组中具体的索引值,*/第二种将区间分成了两块，即 一定不存在目标元素的区间 和 可能存在目标元素的区间 ，我们只分析target位于哪块区间。如果要返回的下标值所表示的元素是需要满足某个条件，而不是一个准确值，可以用这种方法。
例如，让我们找：
- 大于等于 target 的下标最小的元素；
- 小于等于 target 的下标最大的元素。
对应上面两种情况，对区间的分块方式有两种，如下图。
此处还要注意，在区间分块方法二中，对于取到的mid值，去要向上取整（ceil()函数），以防止出现死循环。
亦即当出现low=mid的赋值语句时，要注意对mid值向上取整
如下图 ，当[low,high]区间只有两个元素时，并且nums[mid]≤target：
//区间分块方法一：[low,high]=[low,mid]+[mid+1,high]
while(low<high){
int mid=(low+high)/2;
if(nums[mid]<target)
low=mid+1;
else
high=mid;
}
return high;/*此处返回high和low皆可，因为while循环
退出的条件是low=high*/
//区间分块方法二：[low,high]=[low,mid-1]+[mid,high]
while(low<high){
double low = **,high = **;
double mid=(low+high)/2;
mid=ceil(mid);//向上取整函数,向下取整为函数floor()
if(nums[mid]>target)
high=mid-1;
else
low=mid;
}
return high;/*此处返回high和low皆可，因为while循环
退出的条件是low=high*/
第287题
给定一个包含
n + 1个整数的数组nums，其数字都在1到n之间（包括1和n），可知至少存在一个重复的整数。假设nums只有 一个重复的整数 ，找出 这个重复的数 。设计的解决方案必须不修改数组nums且只用常量级O(1)的额外空间。输入：nums = [3,1,3,4,2] 输出：3
首先根据题目，有一个长度为n+1的数组，里面含有大小为1~n的元素，元素范围的长度为n，而数组的长度为n+1，则一定含有重复的元素，且题目交代只有一个重复元素，那么数组中会有一个到多个的重复元素。
思路是通过二分查找法在1,2,3...n中查找数（注意不是在nums数组中遍历，这一点是本题的关键）
left=1，right=n-1，mid=(left+right)/2 然后统计原始数组中小于等于mid 的元素的个数times：
如果times大于 mid，在1~mid中如果没有重复元素的话，最多有mid个，而times大于mid，则重复元素就在区间[left mid] 里；否则，重复元素就在区间 [mid+1 right] 里。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n=nums.size();
int left=1,right=n-1;
while(left<right){
int mid = (left+right)/2;
int times=0;
for(int num:nums) {
if (num<=mid) times++;
}
if(times<=mid) left=mid+1;
else right=mid;
}
return left;
}
};当然，此题也可以用原地交换数组元素的方法来做，下标从0~n-1分别对应1~n，遍历数组将数组按下标元素由小到大排列，如果遇到不符合顺序的，就交换元素，当发现有元素重复时，返回该元素。代码如下：
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int i = 0;
while(i < nums.size()) {
if(nums[i] == i+1) {
i++;
continue;
}
if(nums[nums[i]-1] == nums[i]) return nums[i];
swap(nums[i],nums[nums[i]-1]);
}
return -1;
}
};
注意此题中运用的循环是while循环而不是for循环，原因在于当遇到顺序不对的元素时，一直交换，直到当前元素与其下标相对应。
第154题/剑指offer11题
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。
输入：[3,4,5,1,2] 输出：1 输入：[2,2,2,0,1] 输出：0
此题比较常规的做法是遍历整个数组，判断相邻两个数的大小关系，更加进阶的做法是二分法，二分法一般用于有序数组的查找，对于此题很难想到用二分法，但可以把此题数组看作两端有序数组，用此题来深化对二分法的使用。
二分法对于区间的划分有两种，一种是将区间分为三块，即:
[low , high]=[low , mid-1]+[mid]+[mid+1,high]
这种划分方法是用来寻找数组中某个特定的值。
另一种划分则是将数组划分为两个区域：可能存在区和一定不存在区。用于查找满足某个条件的值，而不是确切的某个值。划分法如下：
[low , high]=[low , mid-1]+[mid,high] 或 [low , high]=[low , mid]+[mid+1,high]
分析下此题的数组，此题所要寻找的值并不是确切的一个值，所以对于区间的划分用第二种划分方式。具体来看，对于数组，分别有 left，mid，right 三个索引值，数组由两个有序数组组成，numbers[mid]要么在前一个有序数组中，要么在后一个。此题关键就是判断numbers[mid]位于哪一个有序数组中，进而改变left和right的值。
题目要找的是第二个有序数组的第一个元素
- 如果 numbers[mid]<nmubers[right] ，代表numbers[mid]位于后一个有序数组，题目要找的数肯定不在[mid+1,right]中，应该在[left,mid]中继续寻找
- 如果 numbers[mid]>nmubers[right] ，代表numbers[mid]在前一个有序数组中，题目要找的数肯定不在[left,mid]中，应该在[mid+1,high]中继续寻找。
- 如果 numbers[mid]=nmubers[right]，这种情况下，位于两个有序数组中都有可能，此时可将right--，缩小判断范围。此种处理方法较难想到
至于while判断是用 while(left<right)还是 while(left<=right)，考虑当执行到left=right时，此时mid=left=right，数组已经遍历完毕，直接退出即可，不需要再执行while循环体内的语句。所以选用while(left<right)
class Solution {
public:
int minArray(vector<int>& numbers) {
int len=numbers.size();
int left=0,right=len-1,mid;
while(left<right){
mid=left+(right-left)/2;
if(numbers[mid]>numbers[right]) left=mid+1;
else if(numbers[mid]<numbers[right]) right=mid;
else right--;
}
mid=left+(right-left)/2;
return numbers[mid];
}
};二分法的小坑——ceil函数
在求数组中第一个小于target值的元素时，需要将数组分为两个区间求解，在这种情况下，mid的求值要向上取整，需要用到 mid = ceil( (left + right) / 2 ),
但是，需要注意如果此处left和right都是int的话，那么两者和的一半还是int型数，向上取整没有作用。应该改成 mid = ceil( double(left + right) / 2 ）
二分法的变形——寻找两个有序数组的中位数（力扣第四题）
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log (m+n)) 。
输入：nums1 = [1,2], nums2 = [3,4] 输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
此题常规解法是借用归并排序里合并有序数组的方法，但是题目要求时间复杂度是O(log(m+n))；则需要考虑用其他方法，考虑到有序数组并且题目要求的时间复杂度，此题大概率要用到二分法，抛开中位数不谈，首先讨论一下如何求两个有序数组合并后，新的有序数组里的第k个元素。
要查找第k个元素的过程，就是不断确定合并后有序数组中的k/2个，k/2+k/4个，k/2+k/4+k/8个晕元素，......直到确定了k个元素的过程。
解法：
要求合并后的有序数组中的第k大的元素，需要查找nums1的第K/2个元素nums[k/2]和nums2的第k-k/2个元素nums[k-k/2]，这样一共有k个元素，比较这两个元素的的大小；
如果nums1的第K/2个元素小于nums2的第k-k/2个元素的话，即下图橙色部分所示，那么说明合并后的有序数组中的前k个元素中，一定都包含nums1的前K/2个数字。
那么剩下的k-k/2个元素就要在nums1和nums2剩下的元素中寻找，分别在两数组中向后取（k-k/2）个数进行比较，如下图绿色部分所示，nums1的起始位置向后移动K/2个，并且此时的K=(k-k/2)，调用递归。反之，将nums2的起始位置向后移动K/2个，并且此时的K=K/2，调用递归即可。
如此循环往复，直到一个数组遍历完毕，或者k值为1。
注意这里由于两个数组的长度不定，有可能有一个数组nums1从起始位置到数组结束位置的元素个数offset不足k/2个，那么此时此数组nums1直接向将剩下的offset个元素全都取了，另一个数组nums2向后取k-offset个元素，将取得的元素进行比较。
特别的，当某一个数组的起始位置直接在数组的末尾之后，那么此时就没有必要再进行比较了，直接在另一个数组中取起始位置后k个元素即可。
经由上述方法，可以求得两个有序数组合并后的数组汇总的第k个元素。回归到题目中，题目想求的是两个有序数组的中位数，加入合并后的数组有n个数，求其中位数时需要讨论奇偶情况，
当n为奇数是，中位数是。当n为偶数时，中位数是
此处用一个小技巧，直接求
此题的代码可以分为两个部分：求两个有序数组合并后的数组中的第k个元素（findKth函数），以及求一个有序数组的中位数。
class Solution {
public:
int len1,len2;
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
len1 = nums1.size();
len2 = nums2.size();
return (double)( findkth(nums1,0,nums2,0,(len1+len2+1)/2) +
findkth(nums1,0,nums2,0,(len1+len2+2)/2))/2;
}
int findkth(vector<int>& nums1, int start1, vector<int>& nums2, int start2, int k){
if(start1 >= len1) return nums2[start2+k-1];//nums1遍历完毕
if(start2 >= len2) return nums1[start1+k-1];//nums2遍历完毕
if(k == 1) return min(nums1[start1],nums2[start2]);
int offset1,offset2;//代表两个数组中剩下的元素个数
if(len1-start1 < len2-start2){
offset1 = min((len1-start1),k/2);
offset2 = k - offset1;
}
else{
offset2 = min((len2-start2),k/2);
offset1 = k - offset2;
}
if(nums1[start1+offset1-1] > nums2[start2+offset2-1])
return findkth(nums1, start1, nums2, start2+offset2, offset1);
else return findkth(nums1, start1+offset1, nums2, start2, offset2);
}
};动态规划法（Dynamic Programming）（第53题，第62题，第96题，第152题⭐，第221题，第300题，剑指第46题）
个人理解:动态规划法的关键就是创建一个贯穿整个程序的全局变量（通常为一数组vector<int> dp），通过for循环以及状态方程不断更新该全局变量内的数据，并且dp内第i个数据往往表示的是，到当前为止，前i的数据的状态值，例如53题最大子序和表示的是以**结尾的最大和。
动态规划类的题目可以用一句话来描述：到第i步状态时，前i个状态之为**，要求第n步状态。
第53题
理解问题的关键：
数组是 [-2,1,-3,4,-1,2,1,-5,4] ，我们可以求出以下子问题：
子问题 1：经过 -2 的连续子数组的最大和是多少；
子问题 2：经过 1 的连续子数组的最大和是多少；
。。。。。。。。
子问题 9：经过 4 的连续子数组的最大和是多少。
进而演变成：
子问题 1：以 -2 结尾的连续子数组的最大和是多少；
子问题 2：以 1 结尾的连续子数组的最大和是多少；
。。。。。。。。
子问题 9：以 4 结尾的连续子数组的最大和是多少。
子问题i的答案会被子问题i+1利用，亦即子问题之间相互联系，这也是动态规划法的精髓，动态规划法其实就是要找出一种状态，能将在该状态下的子问题能相互联系在一起。
动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。
在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。
依次解决各子问题，最后一个子问题就是初始问题的解。
由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。——百度百科
动态规划法的核心：构造优化解 （即获取状态转换函数） 将前后的子问题联系在一起。
状态转移方程就是带有条件的递推式，定义了问题和子问题之间的关系。
在本例中,状态方程如下图
sum[i]是nums数组中以nums[i]结尾的连续数组的最大值，每一个sum[i]对后面的sum[i+1]都会产生影响。
- 如果 sum[i - 1] > 0，那么可以把 nums[i] 直接接在 sum[i - 1] 表示的那个数组的后面，得到和更大的连续子数组；
- 如果 sum[i - 1] <= 0，那么 nums[i] 加上前面的数 sum[i - 1] 以后值不会变大。于是 sum[i] “另起炉灶”，此时它的值就是一个单独的 nums[i] 值。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int len=nums.size();
int max=nums[0];
vector<int> sum(len,INT_MIN);
sum[0]=nums[0];
for(int i=1;i<len;i++){
if(sum[i-1]>0)//如果当前以nums[i-1]结尾的和不小于0，那么它会对接下来的和有积极影响
sum[i]=nums[i]+sum[i-1];
else
sum[i]=nums[i];如果当前以nums[i-1]结尾的和小于0，那么它被舍弃
if(sum[i]>max)
max=sum[i];//sum[i]表示nums数组中以nums[i]结尾的连续数组的最大值
}
return max;
}
};第62题
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？
两种思路:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> f(m, vector<int>(n));
for (int i = 0; i < m; ++i) {
f[i][0] = 1;
}
for (int j = 0; j < n; ++j) {
f[0][j] = 1;
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
return f[m - 1][n - 1];
}
};class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>>f(m, vector<int>(n,0));
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
if(!i && !j) f[i][j] = 1; //初始化
else{
if(i) f[i][j] += f[i - 1][j]; //如果可以从上方转移过来
if(j) f[i][j] += f[i][j - 1]; //如果可以从左方转移过来
}
return f[m - 1][n - 1];
}
};第96题
搜索二叉树：给定一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种？返回满足题意的二叉搜索树的种数。
示例: n=3 输出 5
思路：假设有数组G，G[n]表示当节点个数为n时，所能构造的搜索二叉树的个数，G[n-1]则表示当节点个数为n-1时，所能构造的搜索二叉树的个数。
求解G[n]时，将1到n分别作为根节点，计算所有可能的搜索二叉树情况。
假设根节点为i，则在以i为根节点的二叉树中，i的左边有i-1个节点，i的右边有n-1个节点，在此种情况下总共有G[i-1]*G[n-1]种可能。
如n=5，i=3时
综上，G[n]是从1到n左右可能的个数之和，可以得出
class Solution {
public:
int numTrees(int n) {
vector<int> G(n + 1, 0);
G[0] = 1;
G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
G[i] += G[j] * G[i - j - 1];
}
}
return G[n];
}
};第221题
在一个由
'0'和'1'组成的二维矩阵内，找到只包含'1'的最大正方形，并返回其面积。
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4
经典的动规题，创建一个二维数组dp[][]，dp[i][j]表示以matrix[i][j]点为右下角的矩阵的最大值。
当matrix[i][j]=0时，dp[i][j]直接为0；当matrix[i][j]=1时，dp[i][j]为dp[i-1][j], dp[i-1][j-1],dp[i][j-1]三者最小值加1;
我的方法：将dp[][]的数组的第一行和第一列单独拿出来初始化，时间会快点
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int row=matrix.size();
int col=matrix[0].size();
int result=0;
vector<vector<int>> dp(row,vector<int>(col,0));
for(int i=0;i<col;i++){
dp[0][i]=matrix[0][i]-'0';
result=max(result,dp[0][i]);
}
for(int i=0;i<row;i++) {
dp[i][0]=matrix[i][0]-'0';
result=max(result,dp[i][0]);
}
for(int i=1;i<row;i++){
for(int j=1;j<col;j++){
if(matrix[i][j]=='0') dp[i][j]=0;
else
dp[i][j]=1+min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]);
result=max(result,dp[i][j]);
}
}
return result*result;
}
};官方题解：简化了代码
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) dp[i][j] = 1;
else
dp[i][j]=min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1])+1;
maxSide = max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};第300题
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入：nums = [10,9,2,5,3,7,101,18] 输出：4 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
- 你可以设计时间复杂度为
O(n2)的解决方案吗？- 你能将算法的时间复杂度降低到
O(n log(n))吗?
时间复杂度O(n2)
见到最长子序列，想到的是用动态规划法，和第59题类似，初始化一个数组dp[]表示动态规划状态量，dp[i]表示以nums[i]结尾的最长严格递增子序列的长度，而有所不同是的是状态转移方程，此题中，dp[i]的值，不光与dp[i-1]有关，dp[i]=max(dp[j])+1 j=0~i-1 && nums[i]>nums[j] ， 即以nums[i]结尾的最长严格递增子序列，等于前i-1个dp[]值的最大值dp[j]+1，并且dp[j]对应的nums[j]要小于nums[i]。代码如下：
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int len=nums.size();
vector<int> dp(len,1);
int res=1;
for(int i=1;i<len;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j])
dp[i]=max(dp[i],dp[j]+1);
}
res=max(dp[i],res);
}
return res;
}
};时间复杂度O(n log(n)) 😵较难
此种方法与动态规划没有什么关系了
上述方法的时间复杂度为O(n2)，即有两个嵌套的for循环，要想将时间复杂度降低，应该将其中一个for循环用其他方法来代替，并且此方法时间复杂度为O(log(n))，可以想到用二分法加一层for循环。因为二分法要求数组有序，所以需要构建一个有序的数组。对其命名为tail[]。
对该数组的定义如下，tail[i]的值表示，数组nums中，长度为i的严格递增子序列的尾部的值，如果有多个子序列的长度都为i，那么nums[i]的值为这几个子序列的尾部元素中的最小值。
可以推断出，这个数组里的值是严格递增的，因为如果后面的数小于前面的数，那么以后面的数结尾的子序列的长度不可能大于以前面的数结尾的子序列。（这个推论属实有点非人类了）
在for循环遍历数组nums的过程中，找到在tail数组中第一个小于nums[i]的元素，如果这个元素是tail数组的最后一个值，那么直接将nums[i]插入tail数组的尾部，否则, 更新该元素后面一个元素的值。
例如nums=[1,2,5,3],当遍历到元素5时，tail[3]=5,而遍历到元素3时，tail[3]=3。因为当前nums数组的严格单调递增子序列有两个：1 2 5和1 2 3，取尾值最小的，所以tail[3]=3。
这样子构建动态数组的目的是让其保证具有单调性，以方便后面用二分法对其进行遍历更新。
tail数组最后一个元素的下标值即题目要求的最长严格递增子序列长度。
class Solution {
private:
vector<int> tail;
public:
int lengthOfLIS(vector<int>& nums) {
int len = nums.size();
tail.push_back(0);
int left, right, index;
for(int i = 0; i < len; i++){
index = findLess(0, tail.size() - 1, nums[i]);
if(index < tail.size() - 1) tail[index + 1] = min(tail[index + 1], nums[i]);
else tail.push_back(nums[i]);
}
return tail.size() - 1;
}
int findLess(int left, int right, int target){
while(left < right){
int mid = ceil((double)(left + right) / 2);
if(tail[mid] >= target) right = mid - 1;
else left = mid;
}
return left;
}
};把数字翻译成字符串 （剑指第46题）
给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。
示例 1: 输入: 12258 输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
法一：乍一看，这题有点像深度优先遍历，那就用深度优先遍历来解，将数字num转换为string类型，每次去掉字符串头部一个或者两个字符，接着对剩下的字符进行同样的操作。至于是去掉一个字符还是去掉两个字符，则要看 stoi( str.substr(0,2) ) 的取值，如果表示的数在10到25之间，则既可以去掉一个，也可以去掉两个，而如果在这范围之外，则只能去掉一个字符，因为首部两个字符构成的字符串不能用题目中的25个字母表示。
class Solution {
public:
int translateNum(int num) {
string str = to_string(num);
return fun(str);
}
int fun(string str){
if(str.length() == 1) return 1;
if(str.length() == 2) return (stoi(str) > 25 || stoi(str) < 10) ? 1 : 2;
string temp = str.substr(0,2);
if(stoi(temp) > 25 || stoi(temp) < 10) return fun(str.substr(1));
else return fun(str.substr(1)) + fun(str.substr(2));
}
};法二：动态规划
状态定义：设动态规划列表 dp，dp[i] 代表以Xi为结尾的数字的翻译方案数量。
转移方程： 若Xi和X(i-1)组成的两位数字可以被翻译，则 dp[i] = dp[i - 1] + dp[i - 2]；否则 dp[i] = dp[i - 1]。
class Solution {
public:
int translateNum(int num) {
string str = to_string(num);
int len = str.length();
vector<int> dp(len + 1, 0);
dp[0] = dp[1] = 1;
for(int i = 1; i < len; i++){
dp[i+1] = dp[i];
int temp = stoi(str.substr(i - 1, 2));
if(temp >= 10 && temp <= 25) dp[i+1] +=dp[i-1];
}
return dp[len];
}
};动态规划是寻找一种对问题的观察角度，让问题能够以递推（或者说分治）的方式去解决。寻找看问题的角度，才是动态规划中最耀眼的宝石！（大悟🙊🙉）
一个问题是该用递推、贪心、搜索还是动态规划，完全是由这个问题本身阶段间状态的转移方式决定的！
每个阶段只有一个状态->递推；
每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心；
每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索；
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到
这个性质叫做最优子结构；
而不管之前这个状态是如何得到的
这个性质叫做无后效性。
动态规划法的进阶——背包问题（322题，416题，494题）
附上一些对背包问题的解释：
给定一个背包容量target，再给定一个数组nums(物品)，能否按一定方式选取nums中的元素得到target
注意：
1、背包容量target和物品nums的类型可能是数，也可能是字符串
2、target可能题目已经给出(显式)，也可能是需要我们从题目的信息中挖掘出来(非显式)(常见的非显式target比如sum/2等)
3、选取方式有常见的一下几种：每个元素选一次/每个元素选多次/选元素进行排列组合
背包问题分类：
常见的背包类型主要有以下几种：
1、0/1背包问题：每个元素最多选取一次
2、完全背包问题：每个元素可以重复选择
3、组合背包问题：背包中的物品要考虑顺序
4、分组背包问题：不止一个背包，需要遍历每个背包而每个背包问题要求的也是不同的，按照所求问题分类，又可以分为以下几种：
1、最值问题：要求最大值/最小值
2、存在问题：是否存在…………，满足…………
3、组合问题：求所有满足……的排列组合背包问题大体的解题模板是两层循环，分别遍历物品nums和背包容量target，然后写转移方程，一般是建立一个长度位容量+1的vector动态数组，根据背包的分类确定物品和容量遍历的先后顺序，根据问题的分类确定状态转移方程的写法
根据做题总结，背包问题中
如果背包内的元素个数无限制，即完全背包问题，那么外层循环遍历的是容量构成的数组；
如果背包内的元素有个数限制，即0/1背包问题，那么外层遍历的是内背包内的元素数组。
第322题
给你一个整数数组
coins，表示不同面额的硬币；以及一个整数amount，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回
-1。你可以认为每种硬币的数量是无限的。
输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1
输入：coins = [2], amount = 3 输出：-1
输入：coins = [1], amount = 0 输出：0
思路一：递归法（超时😭） 但这这道题能很好的锻炼递归法的思维
如下，书写了个函数用来递归，函数退出的条件是当前sum小于或等于0，sum小于0时，代表当前没有合适的硬币，如果sum为0，代表刚好硬币能凑成所需的金额数，这两种情况下都应该退出函数。
另外times表示到当前情况下，所用到的硬币数量，所以每次进入函数时，如果没有很直接退出，那么times应该加一，表示用到的硬币数量又多了一个；同时在函数结束时，需要退出函数，进行回溯操作，此时的times要减一，表示将原来的硬币吐出来，从哪儿来回哪去。
class Solution {
public:
int times=0,res=INT_MAX;
int coinChange(vector<int>& coins, int amount) {
if(amount==0) return 0;
fun(amount,coins);
return res==INT_MAX?-1:res;
}
void fun(int sum,vector<int>& coins){
if(sum<0) return;
if(sum==0){
res=min(times,res);
return;
}
times++;
for(auto num:coins){
fun(sum-num,coins);
}
times--;
}
};后面发现超时后，有优化了下算法，虽然还是超时了，但思想值得学习。
class Solution {
public:
int times=0,res=INT_MAX;
int coinChange(vector<int>& coins, int amount) {
if(amount==0) return 0;
fun(amount,coins);
return res==INT_MAX?-1:res;
}
void fun(int sum,vector<int>& coins){
if(sum<0||times<res) return;//优化了一下
if(sum==0){
res=times;
return;
}
times++;
for(auto num:coins){
fun(sum-num,coins);
}
times--;
}
};思路二：动态规划法
设动态数组 dp[i] 为组成金额 i 所需最少的硬币数量
数组 dp[] 的下标应包括从1到amount在内的一系列连续数字。为了方便表示，设置dp的长度为amount，这样dp数组的下标值就与总金额数相同了。
与一般的情况不同，此题中主要的遍历是从1到amount依次遍历，并对dp[i]赋值，意思就是判断当总金额数为1~amount中的每一个数时（而不仅仅是题目要求的amount），这些数能否被硬币数组coins[]中的元素正确的表示，这么设计是为了方便后面构建状态转移方程。
状态转移方程如下：
与一般的状态转移方程不同，上述状态方程的dp[i]并不是由dp[i-1]得到的，而是在动态数组的多个值内取最小值并加一，这些多个dp[]数组的元素的下标为 i-coins[j] ,dp[i-coins[j]]意思是，对于当前的所求的金额数 i，判断 i-coins[j] 是否存在，即将当前金额 i 分别减去硬币数组coins中的每个元素，查看被减去一个硬币后的金额是否存在，若存在的话将其能用coins数组内的硬币表示的最小硬币个数加一，就得到了金额 i 所能用硬币表示的最小硬币数。
对代码的几个解释：
- dp[]数组内的元素一开始被初始化为 -1，表示元素不能用硬币数组coins里的成员表示。
- 有两层for循环，外层是对从1~amount的循环，用来依次判断每个数是否能被硬币数组的元素表示，内层的循环是对硬币数组内的元素的遍历，用来查看当前金额数减去一个硬币数组内的元素是否存在。
- 退出内层循环的情况有两个：一个是当前金额数减去某个硬币的面额后小于0，此时金额数小于硬币的面额，循环无法进行；另一个是当前金额数减去某个硬币的面额后大于0，但对应的结果在dp数组中作索引值时，值为-1，表示无法被硬币数组表示，既然金额数 i 减去当前硬币面额后的结果无法被硬币数组表示，那么金额i也必定无法被表示，此时直接退出当前循环，继续试下一个硬币值。
- 如果条件都满足，那么要对dp[i]的值取最小值，dp[i]>0?dp[i]:INT_MAX 这个表达式是考虑到，当dp[i]初始值为-1，会影响到最小值的判断，所以在其为负时，将其设置为int型的最大正数。
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,-1);
dp[0]=0;
for(int i=1;i<amount+1;i++){
for(auto num:coins){
if(i-num<0) continue;
else if(dp[i-num]==-1) continue;
dp[i]=min(dp[i-num]+1,dp[i]>0?dp[i]:INT_MAX);
//金钱数不为0，并且能用硬币表示
}
}
return dp[amount];
}
};零钱升级版力扣第518题
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。输入：amount = 5, coins = [1, 2, 5] 输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
此题与上一题类似，都是硬币数量无限，但是与上一题不同的是，此题要求的是对于某一金额，所有硬币的排列组合，如果仍然用外层循环金额数量，内层循环硬币数组的方式的话，得到的结果会大很多。此时的动态方程书写如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}
原因就是 dp[j] += dp[j - coins[i]] 这一语句
举个例子 对于硬币 1 2 5 如果此时金额为 6
6 = 2 + 4；硬币2再加上零钱4
6 = 1 + 5；硬币1再加上零钱5
此时由金额4可以到6，由金额5也可以到6，但如果此时直接将dp[4] + dp[5]，结果会出错，因为实际上从5到6的情况已经被包含在从4到6的路径里了
所以此题的两层循环，外层循环硬币数组，内层循环金额数量。这样子让每一个金额都只是由硬币一个加一个堆成的，不会包含比它小的金额，这样子避免了重复包含硬币组成情况
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount + 1, 0);
dp[0] = 1;
for(auto num : coins){
for(int i = num; i <= amount; i++){
dp[i] += dp[i - num];
}
}
return dp[amount];
}
};第416题
给你一个只包含正整数的非空数组
nums。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11] 。
可以将题目的要求改为：对于一个数组，判断其中是否存在子序列，子序列的和是数组总和sum的一半。这就是一个典型的背包问题， 要求判断数组nums中是否存在一些元素，这些元素之和为sum/2；但是与上面硬币的问题不同，此题中元素只能使用一次，属于0/1背包问题。
代码结构的话照常是两层循环，新建一个动态数组dp。动态数组的长度为sum/2+1，这样dp的下标值与实际值能对上。dp[i]的值有0和1两种情况，dp[i]=0代表，在数组nums中没有子序列的和为i，dp[i]=1则相反。接下来就是比较重要的动态方程：
对于当前的nums遍历值num，遍历dp数组，如果dp[i]=1,代表i能用nums数组中的元素表示，因为num也是nums内的元素，那么显而易见，i+sum也一定可以用nums的子序列来表示。与一般的动态规化不同，此题是由当前状态推出了后续的状态。
并且在列写代码时有一个注意点， dp[0]=1，对于dp的遍历由下标为0开始。在每一轮num中，都会有一个vector数组来存储dp数组中符合条件的下标值，到最后再统一赋值，这是为了避免在遍历过程中，对后续的判断造成影响，因为在循环到num值下，dp中的状态应该还是停留在num之前的值所赋予的，如果此时将num考虑进来，可能会造成二次赋值。
如下，以数组[1,5,3,11]为例，当遍历到5时，由dp[0]=1，可以知道dp[5]=1。如果此时就将dp[5]赋值为1，那么dp数组在遍历到下标5时，又会将下标10赋值为1，这显然是不对的。
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=0,number=0;
for(auto num:nums) sum+=num;
if(sum%2==1) return false;
sum=sum/2;
vector<bool> dp(sum+1,0);
dp[0]=1;
for(auto num:nums){
if(num>sum) return false;
vector<int> temp;//存储当前num下dp数组中符合条件的下标
for(int i=0;i<sum+1;i++) if(dp[i]==1&&i+num<sum+1) temp.push_back(i);
for(auto aa:temp) dp[aa+num]=1;
if(dp[sum]) return true;
}
return false;
}
};优化：上述方法，第二层遍历是从前往后的，会有前面操作影响到后续判断的问题，对第二层遍历进行优化，遍历顺序从后往前，避免了多余的操作，这是0/1背包问题的固定模板
其中 for(int i=sum;i>=num;i--) dp[i] = dp[i]||dp[i-num]?1:0 一句还加入了对于当前dp[i]值的判断，避免出现 当前dp[i]值为1，dp[i-num]为0，将dp[i]置为0的情况。
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=0,number=0;
for(auto num:nums) sum+=num;
if(sum%2==1) return false;
sum=sum/2;
vector<bool> dp(sum+1,0);
dp[0]=1;
for(auto num:nums){
for(int i=sum;i>=num;i--) dp[i] = dp[i]||dp[i-num]?1:0;
if(dp[sum]) return true;
}
return false;
}
};第494题
给你一个整数数组 nums 和一个整数 target 。向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：
例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。返回可以通过上述方法构造的，运算结果等于 target 的不同表达式的数目。
输入：nums = [1,1,1,1,1], target = 3 输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
此题一开始想的是用递归法，对数组内的每一个值，设置两个入口，对应加和减，不断循环往复，直到数组末尾，接着判断总的和是否与target相等。代码如下：
class Solution {
public:
int res=0;
int findTargetSumWays(vector<int>& nums, int target) {
fun(nums,0,0,target);
return res;
}
void fun(vector<int> & nums,int index,int sum,int target){
if(index==nums.size()){
if(sum==target) res++;
return;
}
fun(nums,index+1,sum+nums[index],target);
fun(nums,index+1,sum-nums[index],target);
}
};
但这种方法时间复杂度太高，考虑用动态规划法来完成：
一开始思考时，考虑到这一题，如果把每一个元素的加减情况考虑进去，会产生种情况，所以一开始就把动态规划法排除掉了。如果要用动态规划法来解决，需要将问题换个说法，很多动态规划问题都是如此，难得不是列些动态规划方程，而是将题目转换成符合动态规划的说法。对于此题，可以将要求改为：
对于数组nums，数组中的元素都是正数，判断是否存在数组的两个子集P和H，使得P和H的和sum_p,sum_h满足
sum_p — sum_h = target
sum_p = target + sum_h = target + sum — sum_p
2*sum_p = target + sum
sum_p = (target + sum)/2
最后变为，在数组nums中寻找一个子集P，该子集的和sum_p是 target加上nums左右元素的和的一半。这就变成了一个0/1背包问题。在代码的书写上，还是两层循环，外层遍历背包中的元素，即数组nums中的元素。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(auto num:nums) sum+=num;
target=target+sum;
if(target<0||target&1) return 0; //target&1表示判断target值是否为奇数
target>>=1; //除以2
vector<int> memory(target+1,0);
memory[0]=1;
for(auto num:nums){
if(num>target) continue;
vector<pair<int,int>> temp;
for(int i=0;i<target+1;i++){
if(num+i<target+1&&memory[i]!=0) temp.push_back(pair(i,memory[i]));
}
for(auto index:temp) memory[num+index.first]+=index.second;
}
return memory[target];
}
};优化：因为这是道0/1背包问题，参照上面第416题，将遍历顺序做下调整，会大大减少时间复杂度。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(auto num:nums) sum+=num;
target=target+sum;
if(target<0||target&1) return 0;
target>>=1;
vector<int> memory(target+1,0);
memory[0]=1;
for(auto num:nums){
for(int i=target;i>=num;i--) memory[i]+=memory[i-num];
}
return memory[target];
}
};😈😈投骰子问题——（剑指60题）
把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
此题如果用暴力解法，会导致超时，应该用动态规划法来解决，而此题用动态规划法的关键就是构建出动态数组，用一个二维数组dp[i][j]来表示当前状态，并且dp[i][j]表示当骰子数为i时，i个骰子组成的和为j的情况的个数。当骰子个数为i时，组成的不同值得和的个数最多有6*i种。
class Solution {
public:
vector<double> dicesProbability(int n) {
vector<vector<int>> dp(n+1,vector<int> (6*n+1,0));
vector<double> res;
int number=pow(6,n);
dp[0][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<6*i+1;j++)
for(int k=1;k<7;k++){
dp[i+1][j+k]+=dp[i][j];
}
}
for(auto num:dp[n]){
if(num!=0) res.push_back((double)num/number);
}
return res;
}
};字符串转换的最小操作数（力扣第72题）
给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
插入一个字符； 删除一个字符； 替换一个字符
输入：word1 = "horse", word2 = "ros" 输出：3
解释： horse -> rorse (将 'h' 替换为 'r')； rorse -> rose (删除 'r')； rose -> ros (删除 'e')
竟然是动态规划法（吐血）
构建一个二维数组dp[][]，dp[i][j]代表 word1 中前 i 个字符，变换到 word2 中前 j 个字符，最短需要操作的次数。一般这种字符串的动态规划题，都要在二维数组汇总多加一行一列，来描述字符串中字符数量为0的情况，如下图：
针对dp[i][j]，要着重讨论一下dp[i-1][j-1], dp[i][j-1], dp[i-1][j]这三个元素元素和dp[i][j]的关系。
将dp[i][j]的情况表示如下，分别有两个字符串word1和word2，为了显示方便，此处将两个字符串的长度设置为一样。
先总结来说，dp[i][j]相比于dp[i-1][j],dp[i][j-1],d[i-1]p[j-1], 需要分别执行三次加一操作，这三次加一操作分别对应着增删改中的一个，并且增删改操作是先执行于word1的子字符串(下标从0到i)，使其能够进行dp[i-1][j],dp[i][j-1],d[i-1]p[j-1]对应的子字符串操作。
1.
dp[i-1][j-1] = n表示从以word1[i-1]结尾的字符串转换到以word2[j-1]结尾的字符串所需要的步数为n，那么计算dp[i][j]就是计算以word1[i]结尾的字符串转换到以word2[j]结尾的字符串所需要的步数，可以先经过n步将前word1[i-1]个字符转换完成，再将最后一个字符替换即可。如下，所以从dp[i-1][j-1]到dp[i][j]需要加一，此处加一是替换操作。
2.
dp[i][j-1] = n表示从以word1[i]结尾的字符串转换到以word2[j-1]结尾的字符串所需要的步数为n，那么计算dp[i][j]就是计算以word1[i]结尾的字符串转换到以word2[j]结尾的字符串所需要的步数，可以先经过n步将前word1[i]个字符转换完成，再将最后一个字符加上即可。如下，所以从dp[i-1][j-1]到dp[i][j]需要加一，此处加一是增添操作。
3.
dp[i-1][j] = n表示从以word1[i-1]结尾的字符串转换到以word2[j]结尾的字符串所需要的步数为n，那么计算dp[i][j]就是计算以word1[i-1]结尾的字符串转换到以word2[j]结尾的字符串所需要的步数，可以先将最后一个字符删除，再经过n步将前word1[i-1]个字符转换完成即可。如下，所以从dp[i-1][j-1]到dp[i][j]需要加一，此处加一是删除操作。
特别的，当word1[i]等于word[j]时，dp[i][j] = dp[i-1][j-1]。其他两种情况一样。
class Solution {
public:
int minDistance(string word1, string word2) {
int len1 = word1.size(), len2 = word2.size();
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
for (int i = 1; i < len1 + 1; i++) dp[i][0] = i;
for (int i = 1; i < len2 + 1; i++) dp[0][i] = i;
for (int i = 1; i < len1 + 1; i++){
for (int j = 1; j < len2 + 1; j++){
if (word1[i-1] != word2[j-1])
dp[i][j] = min( {dp[i-1][j-1], dp[i][j-1], dp[i-1][j]} ) + 1;
else
dp[i][j] = min( {dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1]} );
}
}
return dp[len1][len2];
}
};戳气球（力扣第312）
有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。求所能获得硬币的最大数量。
动态规划法（特别版）
我们来看一个区间，这个区间的气球长这样
假设这个区间是个开区间，最左边索引 i，最右边索引 j，此处说 “开区间” 的意思是，只能戳爆 i 和 j 之间的气球，i 和 j 两个不要戳。DP思路如下：
假设此区间最后一个被戳破的气球的索引值为k，此时场上总共剩下三个气球
假设 dp[i][j] 表示开区间 (i,j) 内所能拿到的最多金币，那么这个情况下，在 (i,j) 开区间得到的金币可以由 dp[i][k] 和 dp[k][j] 进行转移，如果此刻选择戳爆气球 k，那么得到的金币数量就是：
total = dp[i][k] + val[i] * val[k] * val[j] + dp[k][j]
对于k，在 (i,j) 开区间可以选的 k 有多个，除了粉色之外，还可以戳绿色和红色，所以需要枚举一下这几个 k，从中选择使得 total 值最大的即可用来更新 dp[i][j]。
因为此题的状态方程需要用二维数组来表示，所以需要构造一个二维的vector，但是与其他的二维动态规划题不同，此题在进行动态规划时的几个for循环的逻辑是从数组nums中出发的，考虑由短到长（开区间i到j的长度h）计算戳气球所得的最大值
class Solution {
public:
int maxCoins(vector<int>& nums) {
int len = nums.size();
vector<vector<int>> dp( len + 2, vector<int>(len + 2, 0) );
vector<int> temp (len+2, 1);
for(int i = 0; i < len; i++) temp[i+1] = nums[i];//为了避免边界问题，在数组两端加上1
for(int length = 2; length < len + 2; length++){//区间的长度(起点减终点)
for(int i = 0; i < len + 2 - length; i++){//区间的起点 对应的的区间的终点的范围是[length, len+2]
for(int k = i + 1; k < i + length; k++){//k对应着起点与终点之间的点
int curr = dp[i][k] + dp[k][i + length] + temp[i] * temp[k] * temp[i + length];
dp[i][i + length] = max(curr, dp[i][i + length]);
}
}
}
return dp[0][len + 1];
}
};双指针法(674题，第11题，第5题，第15题，第19题，第26题）
双指针算法一般用在 数组和链表中，当出现 原地 空间复杂度O(1) 时，优先考虑。
第674题
求一组无序数组中，最长且连续递增的子序列，并返回该序列的长度。
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int len=nums.size();
int l=0,r=0,max=0;
while(r<len){
if(r<len-1&&nums[r+1]>nums[r])
r++;
else{
max=(max>(r-l+1))?max:(r-l+1);
l=r+1;
r=l;
}
}
return max;
}
};😈😈第11题 盛水最多的容器
给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
思路比较难想
此题不应该出成能容纳的最大水的容量，应该改成任意两条边与x轴构成的矩形的最大值，更容易理解一些，最大的容量只与两条边中的较小值有关，与这两条边中间的边的高度无关。。
在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 -1变短：
- 若向内 移动短板 ，水槽的短板 min(h[i], h[j])min(h[i],h[j]) 可能变大，因此下个水槽的面积 可能增大 。
- 若向内 移动长板 ，水槽的短板 min(h[i], h[j])min(h[i],h[j]) 不变或变小，因此下个水槽的面积 一定变小 。
因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。
算法流程：
- 初始化： 双指针 hmin, hmax 分列水槽左右两端；
- 循环收窄： 直至双指针相遇时跳出；
- 更新面积最大值 res ；
- 选定两板高度中的短板，向中间收窄一格；
- 返回值： 返回面积最大值 res 即可；
class Solution {
public:
int maxArea(vector<int>& height) {
int res = 0;
int left = 0, right = height.size() - 1;
while(left < right){
int temp = min(height[left], height[right]) * (right - left);
res = max(temp, res);
if(height[left] < height[right]) left++;
else right--;
}
return res;
}
};第15题 三数之和 滑动窗口加双指针
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 请你找出所有和为 0 且不重复的三元组。注意：答案中不可以包含重复的三元组
输入：nums = [-1,0,1,2,-1,-4] 输入：nums=[ ]
输出：[[-1,-1,2],[-1,0,1]] 输出： [ ]
哈希表解法 自己写的 繁琐 时间空间5%
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> vec;
if(nums.size()<3)
return vec;
unordered_map<int,int> res;
set<int> res_simplify;
set<pair<int,int>> temp;
int a=0;
for(int num:nums){
res[num]++;
res_simplify.insert(num);
}
auto iter=res_simplify.lower_bound(0);
for(auto it=res_simplify.begin();it!=iter;it++){
for(auto it1=iter;it1!=res_simplify.end();it1++){
int b=*it,c=*it1;
a=-(b+c);
if(res[a]==0||a<b||a>c||(b==0&&c==0&&res[0]<3))
continue;
if((a!=b&&a!=c)||
(a==b&&res[a]>1)||(a==c&&res[a]>1))
vec.push_back(vector<int>
{b,c,-(b+c)});
}
}
if(res[0]>2)
vec.push_back(vector<int>{0,0,0});
return vec;
}
};双指针法 时间95% 空间50% 巧妙
vector<vector<int>> threeSum(vector<int>& nums)
{
vector< vector<int> > ans;
if(nums.size() < 3 || nums.empty()) return ans; // 特判
int n = nums.size();
sort(nums.begin(), nums.end()); //排序
for(int i = 0; i < n; i++) // 枚举最小值
{
if(nums[i] > 0) return ans;
if(i > 0 && nums[i] == nums[i-1]) continue; // 最小元素去重！
int l = i+1;
int r = n-1;
while(l < r) // 枚举中间值和最大值
{
int x = nums[l] + nums[r] + nums[i];
if(x == 0){ // 符合条件，存储，并且去重，双端都移到下一个位置
ans.push_back({ nums[i], nums[l], nums[r] });
while( l < r && nums[l] == nums[l+1]) l++; l++;
while( l < r && nums[r] == nums[r-1]) r--; r--;
}
else if(x > 0) // 大了就让右边最大值变小
r--;
else // 小了就让左边中间值变大
l++;
}
}
return ans;
}第19题 删除链表的倒数第n个节点
给定一个链表，删除链表的倒数第 n个结点，并且返回链表的头结点，尝试使用一趟扫描实现。
示例: 输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]
双指针解法：
原理：设定双指针 p 和 q ，当 q 指向末尾的 NULL，p 与 q 之间相隔的元素个数为 n 时，那么删除掉 p 的下一个指针就完成了要求。
- 设置虚拟节点 dummyHead 指向 head
- 设定双指针 p 和 q，初始都指向虚拟节点 dummyHead
- 移动 q，直到 p 与 q 之间相隔的元素个数为 n
- 同时移动 p 与 q，直到 q 指向的为 NULL
- 将 p 的下一个节点指向下下个节点
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* p = dummyHead;
ListNode* q = dummyHead;
for( int i = 0 ; i < n + 1 ; i ++ ){
q = q->next;
}
while(q){
p = p->next;
q = q->next;
}
ListNode* delNode = p->next;
p->next = delNode->next;
delete delNode;
ListNode* retNode = dummyHead->next;
delete dummyHead;
return retNode;
}
};我的解法，遍历依次将所有节点的指针存放在vector<listnode*>内
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
vector<ListNode*> vec;
ListNode* res=head;
while(head!=nullptr){
vec.push_back(head);
head=head->next;
}
int len=vec.size();
int index=len-n;
if(index>0&&index<len-1)
vec[index-1]->next=vec[index+1];
else if(index==0)
res=res->next;
else
vec[index-1]->next=nullptr;
return res;
}
};第26题：删除有序数组的重复项
给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素只出现一次 ，返回删除后数组的新长度。不要使用额外的数组空间，你必须在原地修改输入数组，并在使用 O(1) 额外空间的条件下完成。不需要考虑数组中超出新长度后面的元素。
输入：nums = [0,0,1,1,1,2,2,3,3,4] 输出：5, nums = [0,1,2,3,4]
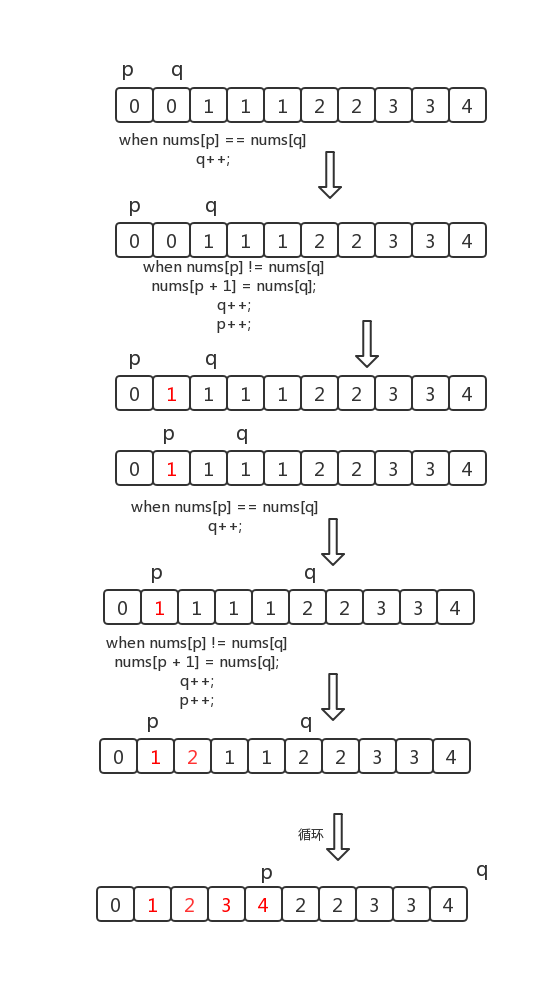
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.size() <= 1)
return nums.size();
int count = 0;
for(int i = 0; i < nums.size() - 1; i++){
if(nums[i + 1] > nums[i])
nums[++count] = nums[i + 1];
}
return (count + 1);
}
};投票法 （169题 一个非常邪门的算法 🐂🍺）
投票法常用于求众数的问题，即求数组中个数大于n/2的数的值(n为数组长度)。
投票法步骤：
- 将候选人(cand_num)初始化为nums[0]，票数count初始化为1；
- 当遇到与cand_num相同的数，则票数count = count + 1，否则票数count = count - 1；
- 当票数count为0时，更换候选人，并将票数count重置为1；
- 遍历完数组后，cand_num即为最终答案。
摩尔投票法的核心就是对拼消耗。
两种解释：
如果候选人不是maj 则 maj,会和其他非候选人一起反对 会反对候选人,所以候选人一定会下台(maj==0时发生换届选举)
如果候选人是maj , 则maj 会支持自己，其他候选人会反对，同样因为maj 票数超过一半，所以maj 一定会成功当选
投票算法有点类似配对，即对于一群人，我们希望知道男的多还是女的多，我们不需要知道多少名男多少名女，而是让一男一女配对，成对的男女离场，看最后场中剩下的是男还是女。
该问题可以理解为数组nums中相同的元素组成各自的队伍，maj所在的队伍人数最多，每个队伍都只支持自己所在的队伍，反对其他所有的队伍。
当赞成和反对某个队伍的人数相同时，我们可以让这些赞成者和反对者组合离场，然后随机选取一个队伍在进行这样的配对和离场。
重点就是这道题中maj所在的队伍人数是大于总人数的一半的，不管怎样配对maj最后一定会被剩下，所以每次随机选取队伍进行“赞成该队伍”和“反对该队伍”的配对清场，不会影响maj队伍人数上的霸权地位。
统计质数（204题 非常有意思👴🏻🤘🏻）
10以内的质数：2，3，5，7
几个优化的关键:
- 采用筛选法，即只要出现了质数a，将a的倍数2a,3a......（叫作合数）都标注起来，后续遍历时直接跳过。具体实现方法为新建一个bool类型的vector，vector的下标为要判断的数，vector的值为0和1，0代表此数为合数，1代表此数为质数。
- 采用奇数遍历，即，偶数一定不是质数，所以只需要对奇数进行遍历，同样的，对质数a的合数进行标记时，只需要对3a，5a，7a.....进行标记。
最终版代码：
class Solution {
public:
int countPrimes(int n) {
if(n<3) return 0;
if(n==3) return 1;
int i=3;//此处直接从3开始遍历，因为只会对奇数进行判断，
//所以2没必要放进来，直接让count加一即可
int count=1;//包含了2
vector<bool> vec(n,1);
while(i<n){
if(vec[i]==0){}
else {
count++;
for(int j=3*i;j<n;j+=2*i)
vec[j]=0;
}
i+=2;
}
return count;
}
};哈希表加滑动窗口（第219题）
哈希表查询数组重复数字（第350题）
DFS（深度优先算法） 岛屿问题（463题,200 题）图像渲染问题（第733题）
网格的DFS遍历，岛屿问题是网格 DFS 问题的典型代表。
网格问题是由m×n 个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子，数字为 1 的格子看成陆地格子，这样相邻的陆地格子就连接成一个岛屿。
DFS算法在二叉树遍历中的应用
void traverse(TreeNode root) {
// 判断 base case
if (root == null) {
return;
}
// 访问两个相邻结点：左子结点、右子结点
traverse(root.left);
traverse(root.right);
}相应的，DFS法在网格遍历中的应用如下
void dfs(vector<vector<char>>& grid,int i,int j) {
if(i<0 || i>=grid.size() || j<0 || j>=grid[i].size() || grid[i][j]=='0' )
return;
if(grid[i][j]!=1)
return;
grid[i][j]==2;// 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid,i,j-1);
dfs(grid,i,j+1);
dfs(grid,i-1,j);
dfs(grid,i+1,j);
}
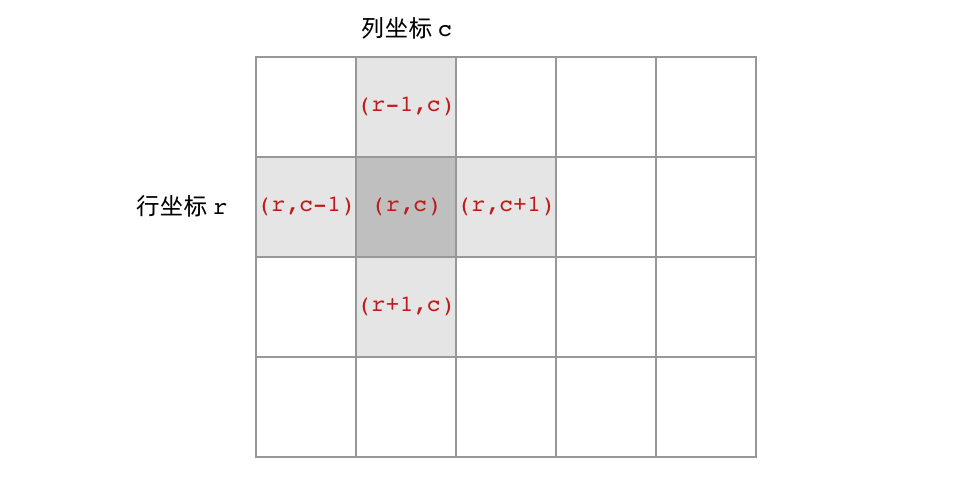
二叉树的相邻结点非常简单，只有左子结点和右子结点两个， DFS 遍历只需要递归调用左子树和右子树即可。与二叉树不同，网格结构中的格子有上下左右四个相邻结点。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)，所以递归调用要对四个结点进行。
其次，二叉树的DFS算法的停止遍历条件为当前根节点为空时返回，网格结构的DFS算法的停止遍历条件为出现数组下标越界异常的格子，也就是那些超出网格范围的格子。
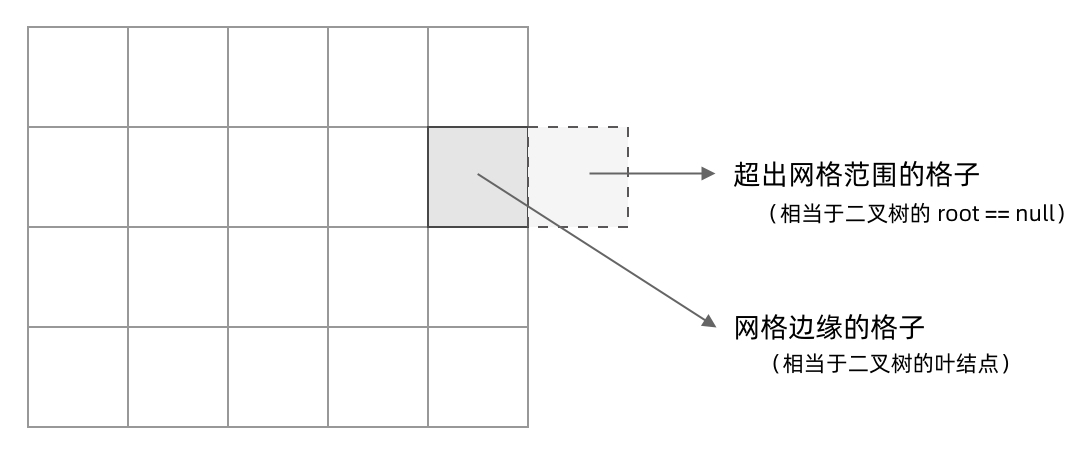
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。这是因为，网格结构本质上是一个「图」，我们可以把每个格子看成图中的结点，每个结点有向上下左右的四条边。在图中遍历时，自然可能遇到重复遍历结点。
通过标记已经遍历过的格子来避免这样的重复遍历。以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。也就是说，每个格子可能取三个值：
0 —— 海洋格子
1 —— 陆地格子（未遍历过）
2 —— 陆地格子（已遍历过）
200题 岛屿数量（提升）
给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围。
输入：grid = [ 输出：3
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
主要思想：逐个遍历，遇到为‘1’则调用fun函数并且岛屿数量加一，进入fun函数后，入口点周围临近的岛屿点都会置为‘0’，这样在退出fun函数，继续其他点的遍历时，不会影响到后续的判断。
class Solution {
private:
void dfs(vector<vector<char>>& grid, int r, int c) {
int nr = grid.size();
int nc = grid[0].size();
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r-1][c] == '1') dfs(grid, r - 1, c);
if (r + 1 < nr && grid[r+1][c] == '1') dfs(grid, r + 1, c);
if (c - 1 >= 0 && grid[r][c-1] == '1') dfs(grid, r, c - 1);
if (c + 1 < nc && grid[r][c+1] == '1') dfs(grid, r, c + 1);
}
public:
int numIslands(vector<vector<char>>& grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
dfs(grid, r, c);
}
}
}
return num_islands;
}
};另一相似题
有一幅以二维整数数组表示的图画，每一个整数表示该图画的像素值大小，数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值（行 ，列）和一个新的颜色值 newColor，让你重新上色这幅图像。
为了完成上色工作，从初始坐标开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像，如下图所示。
class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor{
isequal(image, sr, sc, newColor,image[sr][sc]);
return image;
}
void isequal(vector<vector<int>>& image, int i, int j,int newColor,int oldcolor) {
if (i<0 || i>image.size() - 1 || j<0 || j>image[0].size() - 1||image[i]
[j]==newColor||image[i] [j]!=oldcolor)
return;
image[i][j]=newColor;
isequal(image,i-1, j, newColor,oldcolor);
isequal(image,i+1, j, newColor,oldcolor);
isequal(image,i, j-1, newColor,oldcolor);
isequal(image,i, j+1, newColor,oldcolor);
}
};回溯法的应用：DFS与全排列 （第46题，第47题，第17题，第22题）
回溯法一般都是先列出树状图，根据树状图和模板进行代码的填写。
回溯法的模版参考： 代码随想录
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) 横向遍历
{
处理节点;
backtracking(路径，选择列表); // 递归 纵向遍历
回溯，撤销处理结果// return,删除,置零等操作
}
}
回溯法与深度优先遍历的异同。
两者的不同点如下：
(1)访问的次序不同：深度优先遍历的目的是“遍历”，本质是无序的，重要的是是否被访问过，因此在实现上只需要对于每个位置是否被访问就足够了。回溯法的目的是“求解过程”，本质是有序的，也就是说必须每一步都是要求的次序。
(2)访问次数不同：深度优先遍历对已经访问过的顶点不再访问。回溯法中已经访问过的顶点可能再次访问。
(3)剪枝不同：深度优先遍历不含剪枝。
实际上，除了剪枝是回溯法的一个明显特征外（并非任何回溯法都包含剪枝部分），很难严格区分回溯法 与深度优先遍历。因为这些算法很多是递归算法，在递归调用中隐含着状态的自动回退和恢复。
第46题：输出1~3的全排列：(1,2,3) (1,3,2) (2,1,3) (2,3,1) (3,1,2) (3,2,1)。
力扣 力扣大佬的解说
可以理解为：有编号为1,2,3的三辆车，要将他们停入三个车位，求所有停放的可能。
- book[i]数组用来标记编号为i的车是否停入车库，车始终按从小到大的顺序排列，a[step]为3个车位，step为车位的编号。
- 每次到一个车位时，都要进行一次对book数组从1到n的遍历。按1 2 3的顺序来检查对应号码的车是否停入车位（即book[i]是否为0）
- 直到发现当前车位step为空，并且有车i未停入车位（即book[i]=0），将车i停入
- 或者当前车位step有车停入，但存在未停入车位的车，它的编号比当前step车位内的的车编号更大，将编号更大的车停入
- 接着来到下一个车位前，继续新一轮的遍历。
- 当车位都停满后，从后往前将车开出，继续前面的步骤。
#include<iostream>
using namespace std;
int a[10], book[10];//数组a[]用来存储并输出排列的结果
int n=3;
void dfs(int step) {
/*此时在第step盒子面前，需要往里面放编号为i的扑克牌，只考虑当前盒子的状态
对每个盒子都要进行1~n的遍历，通过book[i]来判断是否填入*/
int i;
if (step == n + 1) { //这里说明前面的n个盒子已经放好了，这是dfs结束的标志
for (i = 1; i <= n; i++)
printf("%d", a[i]);
printf("\n");
return;
/*
注意这个 return 它的作用不是返回主函数，而是返回上一级的dfs函数
例：如果此时是 dfs(5),遇到这个 return 就会回到上一级的 dfs函数
也就是dfs(4),但此时dfs(4)的大部分语句已经执行了，只需要接着执行 book[i]=0
然后继续进入for循环进入下一次的 dfs函数，直到结束。
*/
}
for (int i = 1; i <= n; i++) {/*最主要的是此部分的for循环，for循环代表将
1~n的数依次拿出来验核，若存在数字没有被标记
即book[i]！=1，则把它插入到第step个空位，每次
都是从1~n循环*/
if (book[i] == 0) { //说明i号扑克牌还在手里，需要放入step号盒子
a[step] = i;//将i号扑克牌放到第step个盒子中
book[i] = 1;//此时i号扑克牌已经被使用
dfs(step + 1);
/*如果第step个盒子填入数据，调用下一个
注意这里是自己调用自己，表示此时走到了第step+1个盒子面前*/
book[i] = 0;
/*book[i]=0表示dfs调用结束了，换句话说就是扑克牌已经全部放完了
需要按照顺序将扑克牌收回，重新放，也就是前面所说的
*/
}
}
return;//这里表示这一级别的dfs函数已经结束了，返回上一级 dfs函数
}
int main() {
dfs(1); //dfs函数的开始
return 0;
}
我的另一种解法
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
int len=nums.size();
func(len,nums);
return res;
}
void func(int len,vector<int>& nums){
if(vec.size()==len){
res.push_back(vec);
return;
}
for(int i=0;i<len;i++){
if(count(vec.begin(),vec.end(),nums[i])==0){
vec.push_back(nums[i]);
func(len,nums);
vec.pop_back();
}
}
}
private:
vector<vector<int>> res;
vector<int> vec;
};第47题：
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
与上一题类似， 但是此题中nums中含有重复数字，所以在递归时需要加上剪枝判断的语句。
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
// used[i - 1] == true，说明同一树支nums[i - 1]使用过
// used[i - 1] == false，说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 排序
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
第17题：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母
输入：digits = "23" 输出：["ad","ae","af","bd","be","bf","cd","ce","cf"] 输入：digits = "2" 输出：["a","b","c"]
回溯法与dfs算法的结合
class Solution {
public:
string keyboard[10]={" "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> res;
string s;
vector<string> letterCombinations(string digits) {
if(digits.size()==0)
return res;
func(digits,0);
return res;
}
void func(string &digits,int a){
if(a==digits.size()){
res.push_back(s);
return;
}
int index=digits[a]-'0';
string strnow=keyboard[index];
for(int i=0;i<strnow.size();i++)// 对应着树的横向遍历
{
s.push_back(strnow[i]);//将字符压入s中
func(digits,a+1);//对应着树的纵向遍历
s.pop_back();//将字符从s中依次弹出
}
}
};第22题
数字
n代表生成括号的对数，设计一个函数，用于能够生成所有可能的并且有效的括号组合。有效括号组合需满足：左括号必须以正确的顺序闭合。示例： 输入：n = 3 输出：["((()))","(()())","(())()","()(())","()()()"]
大佬的简洁写法：
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> res;
if(n==0)
return res;
func("",0,0,n,res);
return res;
}
void func(string str,int left,int right,int n,vector<string> &res){
if((left==n)&&(right==n)){
res.push_back(str);
return;
}
if(left<right)
return;
if(left<n) // '('在前
func(str+"(",left+1,right,n,res);
if(right<n) // ')'在后
func(str+")",left,right+1,n,res);
}
};我的写法（不同的回溯撤销操作）
class Solution {
public:
string str;
vector<string> generateParenthesis(int n) {
vector<string> res;
if(n==0)
return res;
func(0,0,n,res);
return res;
}
void func(int left,int right,int n,vector<string> &res){
if((left==n)&&(right==n)){
res.push_back(str);
return;
}
if(left<right)
return;
if(left<n){
str+="(";
func(left+1,right,n,res);
str.pop_back();
}
if(right<n){
str+=")";
func(left,right+1,n,res);
str.pop_back();
}
}
};class Solution {
public:
string str;
int left=0,right=0;
vector<string> generateParenthesis(int n) {
vector<string> res;
if(n==0)
return res;
func(n,res);
return res;
}
void func(int n,vector<string> &res){
if((left==n)&&(right==n)){
res.push_back(str);
return;
}
if(left<right)
return;
if(left<n){
str+="(";
left++;
func(n,res);
str.pop_back();
left--;
}
if(right<n){
str+=")";
right++;
func(n,res);
str.pop_back();
right--;
}
}
};全排列的进阶——打印从1~到最大的n位数（剑指第17题）
输入数字
n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。输入: n = 1 输出: [1,2,3,4,5,6,7,8,9]
分析：本题的考察方式比较简单,当涉及到此类问题时，一般会考察到大数问题，即在n过于大时，所表示的数会超过int型的表示范围，此时就要将计算结果用字符串来表示。
具体的就是将n的每一种情况都进行递归操作，将得到的结果插入string数组中。
代码如下：
class Solution {
private:
vector<int> res;
string num="0123456789";
string s;
public:
vector<int> printNumbers(int n) {
for(int i=1;i<=n;i++) fun(0,i);
return res;
}
void fun(int index,int len){
if(index==len) {
res.push_back(stoi(s));
return;
}
int start = (index==0?1:0);//确定插入的字符是否包含‘0’
for(int i=start;i<10;i++){
s.push_back(num[i]);
fun(index+1,len);
s.pop_back();
}
}
};回溯法 关于 回溯点撤销操作 的处理
如上三段代码，若变量都置于回溯函数fnuc的参数列表内，并且变量的赋值操作也在参数列表内完成，意味着内次进入回溯函数都会新建一个变量，退出时变量被销毁，那么就无需书写撤销操作，如果变量的赋值操作没有在参数列表内完成，意味着变量的生命周期持续在回溯过程全程。则需要在回溯函数尾部加上对应于每个变量的撤销操作。
教做人：单调栈💪👴🍼 （第496题，第739题）
单调栈通常用来解决Next Great Number一类问题，即求不含有重复值的数组 arr 的每一个 i 位置右边离 i 位置最近且值比arr[i]大的元素值。
从字面意思来看，单调栈内的数据按单调性排列。单调栈应用的重点是如何通过pop()和push()指令来实现栈内数据的排列。
上题目：
给你两个 没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ，你无法在第二个数组中找到下一个更大的数字，因此输出 -1 。
对于 num1 中的数字 1 ，第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ，第二个数组中没有下一个更大的数字，因此输出 -1 。
示例 2:输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出 -1 。
单调栈（单调减 从底部向顶部单调递减）构建的伪代码如下：
stack<int> st;
for (遍历这个数组)
{
if (栈空 || 栈顶元素大于等于当前比较元素)
{
当前数组数据入栈;
}
else
{
while (栈不为空 && 栈顶元素小于当前元素)
{
栈顶元素出栈;
更新结果;
}
当前数组数据入栈;
}
}
发现 if与else语句中都进行了当前数据入栈的操作，所以没有必要进行if判断，简化后的单调递减栈如下：
stack<int> st;
for (遍历这个数组)
{
while (栈不为空 && 栈顶元素小于当前元素)
{
栈顶元素出栈;
更新结果;
}
当前数组数据入栈；
}
代码具体如下：
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
stack<int> temp;
map<int,int> exam;
int len=nums2.size();
for(int i=0;i<len;i++){
while(temp.size()!=0&&temp.top()<nums2[i]){
exam[temp.top()]=nums2[i];
temp.pop();
}
temp.push(nums2[i]);
}
while(temp.size()!=0){
exam[temp.top()]=-1;
temp.pop();
}
for(int i=0;i<nums1.size();i++)
nums1[i]=exam[nums1[i]];
return nums1;
}
};图解如下，示例数组[2 1 5 7 3]：
- 遍历数组并将数组中的元素依次压入栈，如果栈内无元素或栈顶元素大于当前压入的元素，直接将元素压入；如果栈顶元素大于当前压入的元素，则将栈顶元素弹出，并且当前压入元素就是弹出的栈顶元素的Next Great Number。
- 如果栈内还存在元素，则重复上述判断，若栈此时为空，则直接压入数据。
- 当数组遍历完毕，都执行完插入操作后，倘若栈内还存在元素，则代表这些元素不存在Next Great Number。
第739题
请根据每日气温列表
temperatures，请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高，请在该位置用0来代替。输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0]
此类求下一个最近的更大值的题目，一般都是用栈来解决。但此题与上面的题不同，上一题要求的是更大的元素的值，所以在栈中保存的是对应的元素的值；此题所要返回的是对应的元素的下标，所以栈中保存的应该也是对应的下标值，并且此题构造的是单调递减栈，碰到大的直接出栈，小的则进栈。具体过程见视频，代码如下：
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> temp;
int len=temperatures.size();
vector<int> res(len,0);
for(int i=0;i<len;i++){
while(!temp.empty()&&temperatures[i]>temperatures[temp.top()]){
res[temp.top()]=i-temp.top();
temp.pop();
}
temp.push(i);
}
return res;
}
};
一道与摆花盆类似的题（第717题）
有两种特殊字符。第一种字符可以用单比特0来表示。第二种字符可以用双比特(10 或 11)来表示。
现给一个由若干比特组成的字符串。问最后一个字符是否必定为一个单比特字符（即比特0）。给定的字符串总是由0结束。
示例 1:
输入:
bits = [1, 0, 0]
输出: True
解释:
唯一的编码方式是一个双比特字符和一个单比特字符。所以最后一个字符是单比特字符。
示例 2:
输入:
bits = [1, 1, 1, 0]
输出: False
解释:
唯一的编码方式是双比特字符和双比特字符。所以最后一个字符不是单比特字符。
由题意，双字符有10和11两种情况，单比特为0一种情况。若字符串能够按单比特和双比特的方式完整地编码，当从左往右遍历时，比特1一定会占有下一个比特，无论下一个比特是0还是1，即便遍历遇到比特1时，直接跳过一个比特进行判断。
class Solution {
public:
bool isOneBitCharacter(vector<int>& bits) {
int len=bits.size();
int i=0;
while(i<len-1){
if(bits[i]==1)
i+=2;
else
i++;
}
if(i==len)
return false;
else
return true;
}
};贪心算法（第55题）
给定一个非负整数数组 nums ，最初位于数组的第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断是否能够到达最后一个下标。
示例 1：
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
遍历nums数组，每遍历一个更新一次最大可达距离k，如果当前下标大于最大可达距离k，表示该元素不可达，最后一个元素也不可达，如果最大可达距离k大于最后一个元素的下标，则最后一个元素可达。主要的就是将最大可达距离k与nums数组中的每个元素分离开来，k表示的是目前nums能到达的是下标从0到k部分的数据，始终都是表示从0到k部分，而不是只表示从某个下标到k。
大佬的代码
class Solution {
public:
bool canJump(vector<int>& nums) {
int k = 0;
for (int i = 0; i < nums.size(); i++) {
if (i > k) return false;
k = max(k, i + nums[i]);
if(k>nums.size()-2) break;
}
return true;
}
};
滑动窗口
第643题
class Solution {
public:
double findMaxAverage(vector<int>& nums, int k) {
int sum = 0;
int n = nums.size();
for (int i = 0; i < k; i++) {
sum += nums[i];
}
int maxSum = sum;
for (int i = k; i < n; i++) {
sum = sum - nums[i - k] + nums[i];
maxSum = max(maxSum, sum);
}
return double(maxSum) / k;
}
};第438题
给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。
输入: s = "cbaebabacd", p = "abc" 输出: [0,6]
对于此题，可以转换成：在字符串数组s中，依次判断以每个字符开头，长度与字符串p长度相同的字符串是否为p的异位词字符串，即对于s中的每个元素都要进行判断，因为每次欧安短的字符串的长度是不变的，所以可以考虑用滑动窗口来实现。
具体来说，就是在s中构建一个滑动窗口，比较窗口内的元素与p是否为异位词，判断的过程用两个数组来实现，数组长度为26，对应26个小写字母，遍历窗口和p，记录下每个字母出现的次数，比较两个数组中每个字母出现的次数是否相等。
当窗口向后滑动一个单位时，不必将窗口内的数据再次重新统计个数，因为发生变化的只有窗口头尾两个元素，在数组中，将窗口尾部元素对应下标加一，头部元素对应下标减一即可。
我的解法：
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> res;
vector<int> s_word(26), p_word(26);
int len_p=p.size(), len_s=s.size();
if(len_p>len_s) return res;
bool sign;
for(int i=0;i<len_p;i++) {
s_word[s[i]-'a']++;
p_word[p[i]-'a']++;
}
for(int i=0;i<=len_s-len_p;i++){
sign=1;
for(int j=0;j<26;j++){
if(s_word[j]!=p_word[j]) {
sign=0;
break;
}
}
if(sign) res.push_back(i);
if(i<len_s-len_p) {
s_word[s[i+len_p]-'a']++;
s_word[s[i]-'a']--;
}
}
return res;
}
};😈和为s的连续正数序列（剑指第57题 ）
输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。
输入：target = 15 输出：[[1,2,3,4,5],[4,5,6],[7,8]]
设连续正整数序列的左边界 i 和右边界 j ，则可构建滑动窗口从左向右滑动。循环中，每轮判断滑动窗口内元素和与目标值 target的大小关系，若相等则记录结果，若大于 target 则移动左边界 i （以减小窗口内的元素和），若小于 target则移动右边界 j（以增大窗口内的元素和）。
算法流程：初始化： 左边界 i = 1，右边界 j = 2，元素和 s = 3，结果列表 res ；
循环： 当 i ≥j 时跳出；
当 s > targets 时： 向右移动左边界 i = i + 1 ，并更新元素和 s ；
当 s < targets 时： 向右移动右边界 j = j + 1 ，并更新元素和 s ；
当 s = targets时： 记录连续整数序列，并向右移动左边界 i = i + 1 ；
返回值： 返回结果列表 res；
class Solution {
public:
vector<vector<int>> findContinuousSequence(int target) {
vector<vector<int>> res;
int i=1,j=2,sum=0;
sum=i+j;
while(i<j){
if(sum>target){
sum-=i;
i++;
}
else if(sum<target){
j++;
sum+=j;
}
else{
res.push_back(vector<int> ());
for(int a=i;a<=j;a++) res.back().push_back(a);
sum-=i;
i++;
}
}
return res;
}
};矩阵/二维数组相关
新思路：矩阵重排（第556题）
在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。
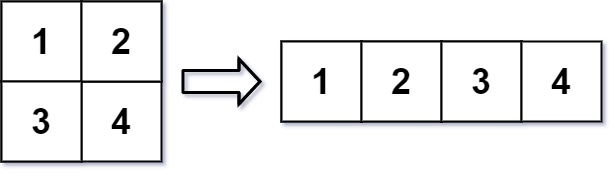
输入：mat = [[1,2],[3,4]], r = 1, c = 4 输出：[[1,2,3,4]]
输入：mat = [[1,2],[3,4]], r = 2, c = 4 输出：[[1,2],[3,4]]
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
int m = nums.size();
int n = nums[0].size();
if (m * n != r * c) {
return nums;
}
vector<vector<int>> ans(r, vector<int>(c));
for (int x = 0; x < m * n; ++x) {
ans[x / c][x % c] = nums[x / n][x % n];//太妙了
}
return ans;
}
};
一种相对简洁的遍历矩阵写法（第661题）
包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ，平均灰度的计算是周围的8个单元和它本身的值求平均，如果周围的单元格不足八个，则尽可能多的利用它们。
示例 1:
输入: 输出:
[ [1,1,1], [ [0, 0, 0],
[1,0,1], [0, 0, 0],
[1,1,1] ] [0, 0, 0] ]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0
注意:给定矩阵中的整数范围为 [0, 255]。
矩阵的长和宽的范围均为 [1, 150]。
class Solution {
public:
vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
const int n = img.size();
const int m = img[0].size();
vector<vector<int>> ans(n, vector<int>(m,0));
for(int i = 0; i < n; ++i){ //遍历每一个点
for(int j = 0; j < m; ++j){
int sum = 0, count=0;
for(int k=-1;k<2;k++){//对每个点周围八个点以及其本身判别
for(int l=-1;l<2;l++){
if((i+k>-1)&&(i+k<n)&&(j+l>-1)&&(j+l<m)){
count++;
sum+=img[i+k][j+l];
}
}
}
ans[i][j]=(sum/count);
}
}
return ans;
}
};矩阵顺时针旋转的解法（第48题）
给定一个n×n的二维矩阵matrix表示一个图像。将图像顺时针旋转 90 度。你必须在原地旋转图像，这意味着直接修改输入的二维矩阵。
示例：输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]]
思路：先将矩阵沿中间一行对称，再沿矩阵副对角线（左下和右上连线）转置
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int len=matrix.size();
int temp;
for(int i=0;i<len/2;i++)
swap(matrix[i],matrix[len-1-i]);
for(int i=0;i<len;i++){
for(int j=0;j<i;j++){
temp=matrix[j][i];
matrix[j][i]=matrix[i][j];
matrix[i][j]=temp;
}
}
}
};矩阵的顺时针遍历（第54题）
给你一个
m行n列的矩阵matrix，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]
没什么好说的，就是分四次遍历，遍历完更新下二维数组的上下左右四个边界值
class Solution {
private:
vector<int> res;
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
fun(matrix,0,matrix.size()-1,0,matrix[0].size()-1);
return res;
}
void fun(vector<vector<int>>& matrix,int up,int down,int left,int right){
if(up>down||left>right) return;
for(int i=left;i<=right;i++){
res.push_back(matrix[up][i]);
}
for(int i=up+1;i<=down;i++){
res.push_back(matrix[i][right]);
}
for(int i=right-1;i>=left;i--){
if(down>up) res.push_back(matrix[down][i]);//防止重复遍历
}
for(int i=down-1;i>up;i--){
if(right>left) res.push_back(matrix[i][left]);//防止重复遍历
}
fun(matrix,up+1,down-1,left+1,right-1);
}
};矩阵元素的遍历（十字型）
一段代码，用来访问矩阵每一个元素的，上下左右四个元素,就是建立一个索引值的增量数组：
vector<int> dx{0,0,1,-1};
vector<int> dy{1,-1,0,0};
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
for(int a=0;a<4;a++){
int x=i+dx[a],y=j+dy[a];
if(x>-1&&x<m&&y>-1&&y<n){...}
}
}
}😈搜索二维矩阵（第240题）
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：每行的元素从左到右升序排列；每列的元素从上到下升序排列。如下：
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
解题的思路非常精妙，一张图足矣：
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int row=matrix.size();
if(row==0) return false;
int col=matrix[0].size();
int i=0,j=col-1;
while(i<row&&j>-1){
if(matrix[i][j]==target) return true;
else if(matrix[i][j]>target) j--;
else i++;
}
return false;
}
};😈 矩阵中单词的搜索（第79题）
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
此题首先要用到上面矩阵元素的十字型遍历法，主要的思想是遍历二维矩阵，对于数组中的每一个元素，都对其进行字符串从头到尾的判断，如果当前元素等于字符串word第一个字符，则判断该元素上下左右四个元素是否等于字符串word的第二个字符，依次进行，直到判断到了字符串的尾部元素。代码如下：
class Solution {
public:
vector<int> index_x, index_y;
int m, n, len;
bool exist(vector<vector<char>>& board, string word) {
m = board.size();
n = board[0].size();
len = word.size();
index_x = {1, -1, 0, 0};
index_y = {0, 0, -1 ,1};
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if( fun(board, word, i, j, 0) ) return true;
}
}
return false;
}
bool fun(vector<vector<char>>& board, string &word, int i, int j, int index){
if(i < 0 || j <0 || i >= m || j >= n || board[i][j] == '.' || board[i][j] != word[index])
return false;
if(index == len - 1) return true;
board[i][j] = '.';
for(int k = 0; k < 4; k++){
if (fun(board, word, i + index_x[k], j + index_y[k], index + 1)) return true;
else continue;
}
board[i][j] = word[index];
return false;
}
};机器人运动范围——数位之和(个位，十位，百位...之和)（剑指 13题）
地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？
输入：m = 2, n = 3, k = 1 输出：3
此题也是一道典型的矩阵遍历题，但是与上一题不同的是， 上一题中矩阵中的所有元素都可以到达，剪枝条件是路径上的单词与目标字符串相同，而此题中矩阵的元素并不都能到达，对应的剪枝条件是矩阵中行与列的数位之和要小于等于k。那么对应的遍历策略就不一样了，或者说递归函数的书写方式就不一样了。
上一题中，矩阵的中各个元素之间都有联系，因为要将其串成目标字符串，因此要对矩阵中的每个元素都要将其作为起点进行遍历，而此题中的矩阵的元素之间不需要有联系，对于每一个元素只需要遍历过即可，所以可以将矩阵的左上角作为起点，一路向下和向右遍历即可。
此题中，比较关键的是对数位之和的计算。对于一个数a，其数位之和的计算可以表示成
int sums(int x)
int s = 0;
while(x != 0) {
s += x % 10;
x = x / 10;
}
return s;此题中，矩阵元素每一次移动一格，对应下都是加一的关系，所以可以建立关于数位和的动态方程：
设a的数位和为
，则a+1的数位和为
；
当a+1为10的倍数时，
，如从19到20；
当a+1不是10的倍数时，
，如从18到19。
s_x_plus = (x + 1) % 10 != 0 ? s_x + 1 : s_x - 8;
代码如下：
class Solution {
private:
int col,row,goal;
public:
int movingCount(int m, int n, int k) {
col=n,row=m,goal=k;
vector<vector<bool>> visited(m, vector<bool>(n, 0));
return dfs(0, 0, 0, 0, visited);
}
private:
int dfs(int i, int j, int si, int sj, vector<vector<bool>> &visited) {
if(i >= row || j >= col || goal < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj, visited) +
dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8, visited);
//当前节点(一个)加上下方符合条件加上右方符合条件的元素个数
}
};不带返回值的递归：
class Solution {
public:
vector<vector<bool>> vec;
int res,M,N;
vector<int> index_i, index_j;
int movingCount(int m, int n, int k) {
M = m;
N = n;
vec = vector<vector<bool>> (m, vector<bool>(n, false));
res = 0;
index_i = {1, -1, 0, 0};
index_j = {0, 0, 1, -1};
fun(0, 0, k);
return res;
}
void fun(int i, int j, int &k){
if (i < 0 || i >= M || j < 0 || j >= N || vec[i][j]) return;
if (CalVal(i, j) > k) return;
vec[i][j] = true;
res++;
for(int a = 0; a < 4; a++) fun(i + index_i[a], j + index_j[a], k);
}
int CalVal(int &i, int &j){
return (i/100 + (i == 100 ? 0 : i/10) + i%10 + j/100 + (j == 100 ? 0 : j/10) + j%10);
//已知i j 的值在1到100之间时的简便写法
}
};二叉树
二叉树的三种遍历（递归和非递归实现）
递归法（三种遍历法对应的 res.push_back(root->val) 语句位置不同）：
前序遍历
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
func(root);
return res;
}
void func(TreeNode* root){
if(root==nullptr) return;
res.push_back(root->val);
func(root->left);
func(root->right);
}
};中序遍历
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
func(root);
return res;
}
void func(TreeNode* root){
if(root==nullptr) return;
func(root->left);
res.push_back(root->val);
func(root->right);
}
};后序遍历
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
func(root);
return res;
}
void func(TreeNode* root){
if(root==nullptr) return;
func(root->left);
func(root->right);
res.push_back(root->val);
}
};迭代算法(非递归算法)：中序遍历(第94题) 重难点 需要好好理解
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
TreeNode * curr=root;
while(!st.empty()||curr!=NULL){
while(curr!=NULL){ //对传入循环体的节点，遍历其左节点并入栈
st.push(curr);
curr=curr->left;
}
curr=st.top();
st.pop();
res.push_back(curr->val);//以上三行代码是为了将栈顶部元素弹出并记录其值
curr=curr->right;//对右子节点进行下一轮的循环，若有右子节点为NULL，则
//下一轮while循环中，会将栈中右子节点的父节点的父节点(双重)弹出
}
return res;
}
};迭代算法：前序遍历
写法一(对照递归算法)：
思路如下：
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if (!root) return;
vector<int> result;
stack< TreeNode* > s;
s.push(root);
while (root || !s.empty()) { //s.empty()为真表示函数栈内的所有函数帧
//都已压入和弹出完毕，应退出函数。
while (root) {
result.push_back(node->val);
s.push(root); //root的压入，相当于进入了新的fun(root)函数
root = root->left;//fun(root->left)的递归调用
}
root = s.top();
s.pop(); //退出内层函数，返回至上层函数
root = root->right; //fun(root->right)的递归调用
}
}
写法二：
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
result.push_back(node->val);
//因为栈先入后出的特点，所以要先将右节点压入
if (node->right) st.push(node->right); // 右（空节点不入栈）
if (node->left) st.push(node->left); // 左（空节点不入栈）
}
return result;
}
};迭代算法：后序遍历
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序
if (node->right) st.push(node->right); // 空节点不入栈
}
reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
return result;
}
};😈二叉树的层序遍历（广度优先遍历BFS）（第102题）
给定一个二叉树，返回其按层序遍历得到的节点值。即逐层地，从左到右访问所有节点。
示例：二叉树：[3,9,20,null,null,15,7] 输出：[ [3], [9,20], [15,7] ]
与二叉树的深度优先遍历使用栈不同，二叉树的广度优先遍历使用了队列结构，一般二叉树的BFS算法如下：
void BFS() {
std::queue<Node *> q;
q.push(root);
while (!q.empty()) {
Node *node = q.front();
q.pop();
std::cout << node->key << " ";
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
此题中，要将每一层的节点分批输出，则在每一层遍历开始前，先记录队列中的结点数量 n（也就是这一层的结点数量），然后集中处理完n个结点。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector <vector <int>> ret;
if (!root) return ret;
queue <TreeNode*> q;
q.push(root);
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector <int> ());
for (int i = 1; i <= currentLevelSize; ++i) {
auto node = q.front();
q.pop();
ret.back().push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
};
二叉树层序遍历进阶（剑指第32题）
请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。
给定二叉树: [3,9,20,null,null,15,7], 返回其层次遍历结果：
3 [
/ \ [3],
9 20 [20,9],
/ \ [15,7]
15 7 ]
此题依旧是要求层序便利二叉树，但是遍历的结果要求是之字形，与上一题类似，层序遍历的代码不变，改变的是向vector<vector<int>> res的成员数组填入数据时，是选择在首部填入还是尾部填入。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
deque<TreeNode*> memory;
if(!root) return res;
memory.push_front(root);
bool sym=false;
while(!memory.empty()){
int curr_size=memory.size();
res.push_back(vector<int> (curr_size,0));
TreeNode * node = new TreeNode;
for(int i=0;i<curr_size;i++){
node=memory.front();
memory.pop_front();
res.back()[sym?curr_size-1-i:i]=node->val;
if(node->left) memory.push_back(node->left);
if(node->right) memory.push_back(node->right);
}
sym=!sym;
}
return res;
}
};对称二叉树（第101题）
给定一个二叉树，检查它是否是镜像对称的，用迭代法和递归法分别解题。
二叉树
[1,2,2,3,4,4,3]是对称的1 / \ 2 2 / \ / \ 3 4 4 3
[1,2,2,null,3,null,3]则不是镜像对称的1 / \ 2 2 \ \ 3 3
递归法：带返回值的递归函数一直难以掌握
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return check(root, root);
}
bool check(TreeNode *p, TreeNode *q) {
if (!p && !q) return true;//都为空
if (!p || !q) return false;//有一个为空 不成立
if (p->val != q->val) return false;
return ( check(p->left, q->right) && check(p->right, q->left) );
}
};
迭代法：迭代法一般是与另一种数据结构结合，来模拟函数参数的传递。
class Solution {
public:
bool isSymmetric(TreeNode* root) {
stack<TreeNode *> memory;
memory.push(root);
memory.push(root);//函数的入口，将两个参数压入
while(!memory.empty()){//当栈为空时，表示所有的函数都已结束，栈中存储的临时变量都被弹出
TreeNode * a1=memory.top(); memory.pop();
TreeNode * a2=memory.top(); memory.pop();//取出栈定元素进行操作
if(!a1&&!a2) continue;
if(!a1||!a2) return false;
if( (a1->val)!=(a2->val) ) return false;
//push代表进入其下的子函数
memory.push(a1->left);
memory.push(a2->right);
memory.push(a1->right);
memory.push(a2->left);
}
return true;
}
};扩展讨论:递归与栈，队列的关系
对于二叉树，一般来说，DFS算法用stack，BFS算法用queue，这与两种遍历算法的节点访问与退出顺序有关。
DFS对问题的处理顺序，是遵循了先入后出（先开始的问题最后结束）的规律，符合栈这种数据结构的特性。当调用一个函数的时候，编译器会把这个函数的所有参数及其返回地址都压入栈中，当这个函数退出而结束执行时，这些值从栈中被弹出，栈中的push操作与pop操作对应着进入函数和退出函数。
BFS对问题的处理遵循先后先出的原则，其他与上述类似。
一些个人的理解：当用栈来模拟递归法的过程时，栈用来存储函数的形参值，栈的长度代表着进入子函数的深度(或层数),当栈的长度为0时，表示当前模拟的递归函数都已返回完毕，将退出函数。栈中的元素不断压入，表示一层一层地进入函数，当栈中的元素弹出时，代表当前函数已经运行结束，对应的临时变量要从栈中弹出。
搜索二叉树的后序遍历（剑指第33题）
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回
true，否则返回false。假设输入的数组的任意两个数字都互不相同。例如对于二叉树：
5 输入: [1,6,3,2,5] 输出: false / \ 2 6 输入: [1,3,2,6,5] 输出: true / \ 1 3
对于二叉搜索树的考察，二叉搜索树中序遍历得到的数是由小到大排列的， 后序遍历得到的数组虽然没有严格按照由小到大的规律排列，但还是有一定顺序。因为后序遍历是按照左子结点，右子节点，根节点的顺序将数据压入vector数组。如下：
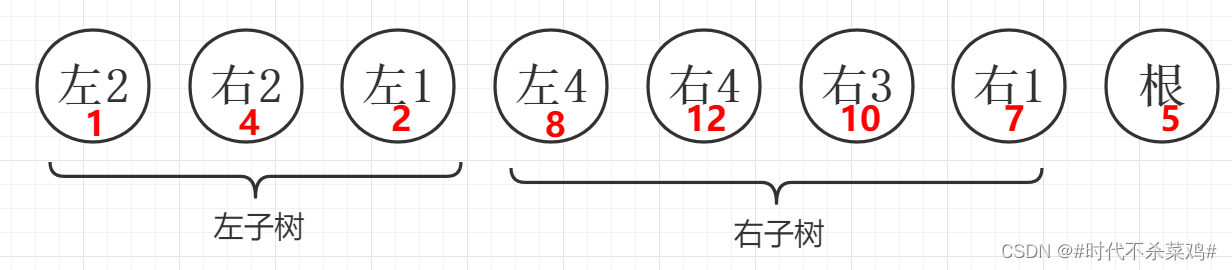
由上图可知，当一个搜索二叉树进行后序遍历时，得到的数据由三部分组成，左子树，右子树，根节点。并且观察可知，根节点的值要大于左子树中所有节点的值，根节点的值要小于右子树中所有节点的值。 所以本题的关键就是对数组进行分段，将其分为上述的三个部分。
易得在当前数组的尾部元素即根节点，接着就是将数组剩下的数据分出左子树和右子树两部分，可以从左向右遍历数组，找到第一个大于数组尾部元素的值，以该值为分界点，可将数组剩下的数据分成两部分，最后只要判断右子树中的元素是否都大于数组尾部数据即可（因为左子树在之前的遍历过程中已经确保了左子树的元素都小于尾部元素）。
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
return fun(postorder, 0, postorder.size()-1);
}
bool fun(vector<int> & postorder, int left, int right){
if (left >= right) return true;
int index = left;
while (index < right && postorder[index] < postorder[right]) index++;
for (int j = index; j < right; j++){
if (postorder[j] < postorder[right]) return false;
}
return fun(postorder, left, index - 1) && fun(postorder, index, right-1);
}
};合并二叉树（ 第617题） 带返回值的递归算法
二叉树的子节点与父节点有一定关系，采用递归算法时一般都要用含返回值的
给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。
可以确定，此题要用到深度优先遍历，但是遍历的细节需要注意。像这种涉及到节点指针值赋值的题型，一般都要采用带返回值的回溯函数。
新建一个二叉树，二叉树的节点值由题目中对应的两个二叉树决定，分几种情况：
- 如果两个二叉树的两个节点有一个为空节点，则新节点为不为空的那个节点
- 如果两个二叉树的两个节点都为空，则新节点也为空
- 如果两个二叉树的两个节点都不为空，则新节点的值为两个二叉树对应节点的和
1 2两点可以合并起来表达，将上述条件整合起来，变成代码就是：
if(!root1) new_node = root2;
else if(!root2) new_node = root1;
else new_node=new TreeNode(root1->val+root2->val);
将其与深度优先遍历结合起来：
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
return fun(root1,root2);
}
TreeNode * fun(TreeNode * root1,TreeNode* root2){
if(!root1) return root2;
if(!root2) return root1;
TreeNode* new_node=new TreeNode(root1->val+root2->val);
new_node->left=fun(root1->left,root2->left);
new_node->right=fun(root1->right,root2->right);
return new_node;
}
};😈😈二叉树展开为链表（第114题） 对二叉树遍历算法的进一步深化
给你二叉树的根结点 root ，请你将它展开为一个单链表：
- 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
输入：root = [1,2,5,3,4,null,6] 输出：[1,null,2,null,3,null,4,null,5,null,6]
解法一：
前序遍历的顺序是中左右，如果按前序遍历的方式修改节点，上述例子中，前序遍历的结果为
1 -> 2 -> 3 -> 4 -> 5 -> 6，一种思路为按前序遍历的顺序，将下一节点改为上一个节点的右节点，但这种方法存在着问题，当某个节点的右节点被替换后，后面的前序遍历的顺序就发生了改变，以至于后续的遍历无法进行。即前面的结果会影响到后面的结果。
解决办法：按前序遍历的逆序来进行，即6 ->5 ->4 ->3 ->2 ->1，将当前节点设置为前一个节点的右节点。
class Solution {
public:
TreeNode * tmp =nullptr;
void flatten(TreeNode* root) {
func(root);
}
void func(TreeNode * root){
if(root==nullptr) return;
func(root->right);
func(root->left);//以上三行是常规的前序遍历程序，
//因为是前序遍历的逆序，即右中左，对左右节点的调用顺序做了调整
root->left=nullptr;
root->right=tmp;
tmp=root;//全局变量tmp记录当前节点，并在下一次递归循环时，赋值给节点的右节点
}
};通过以上程序理解递归的执行顺序：
下面三行代码，是在二叉树遍历到最右下角节点开始执行，执行结束后，到达该此节点func函数的底端，退出该节点的func函数，返回至上一个节点的func函数，程序继续执行。所以这三行代码，是自底向上按节点6 ->5 ->4 ->3 ->2 ->1的顺序执行的。
root->left=nullptr;
root->right=tmp;
tmp=root;解法二：
前序遍历一遍二叉树，将得到的结果存储在一个数组内，然后对数组内的节点进行重排。
此解法一个关键的地方是将节点（TreeNode *形式）直接存进数组，而不是将节点内的值（val）存进数组。当存入数组后，按照数组中节点的前后顺序依次将节点重新进行链接，倘若数组中存储的是节点里的值，重构二叉树比较困难。
class Solution {
public:
void flatten(TreeNode* root) {
vector<TreeNode*> vec;
preorderTraversal(root, vec);
int n = vec.size();
for (int i = 1; i < n; i++) {
TreeNode *prev = vec[i - 1], *curr = vec[i];
prev->left = nullptr;
prev->right = curr;
}
}
void preorderTraversal(TreeNode* root, vector<TreeNode*> &vec) {
if (root != NULL) {
vec.push_back(root);
preorderTraversal(root->left, vec);
preorderTraversal(root->right, vec);
}
}
};二叉树的最大深度——带返回值递归函数和无返回值递归函数之间的转换（第104题）
给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
给定二叉树 [3,9,20,null,null,15,7]，
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
带返回值递归法
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) return 0;
return max( maxDepth(root->left), maxDepth(root->right) ) + 1;
}
};无返回值递归法
class Solution {
public:
int the_max=0;
int maxDepth(TreeNode* root) {
if(!root) return 0;
fun(root,0);
return the_max;
}
void fun(TreeNode * node,int depth){
depth++;
the_max=max(the_max,depth);
if(!node->left&&!node->right) return;
if(node->left) fun(node->left,depth);
if(node->right) fun(node->right,depth);
}
};二叉树深度进阶之一——（第543题）
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
此题相当于求解一个节点的左子树和右子树的深度，将两者的深度相加，就得到了当前过节点的直径长度，此题有一个注意点，直观上似乎只需要求的根节点的左右子树的深度相加即可，但也会存在二叉树的直径长度不会经过根节点的情况，如下：
应该维护一个全局数据，在二叉树遍历到最底部开始回溯时，不断更新全局数据。
class Solution {
public:
int res=0;
int diameterOfBinaryTree(TreeNode* root) {
fun(root);
return res;
}
int fun(TreeNode * node){
if(!node) return 0;
int l=fun(node->left);
int r=fun(node->right);
res=max(res,l+r);
return max(l,r)+1;
}
};二叉树深度进阶之二——（剑指第55题 Ⅱ）
输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。
1 输入：[1,2,2,3,3,null,null,4,4] / \ 输出：false 2 2 / \ 3 3 / \ 4 4
此题也是关于二叉树的深度，关于此题有两种解法：
第一种是书写一个计算节点深度的辅助函数，接下来以根节点root为起点，从上至下依次检查每个节点的左右子树的深度之差是否小于等于1。
class Solution {
public:
bool sym;
bool isBalanced(TreeNode* root) {
sym = true;
int temp = depth(root);
return sym;
}
int depth(TreeNode * node){//计算当前节点深度的辅助函数
if(!node) return 0;
int left = depth(node -> left),right = depth(node -> right);
if(abs(left - right) > 1)
sym = false;
return max(left, right) + 1;
}
};第二种则是自下向上遍历， 其中fun函数返回的是当前节点到叶节点的最大深度，并且在其中加入了剪枝语句，当出现返回值为-1时，代表以该节点为根节点的树不是平衡树，而出现这种情况的原因有两个：1.该节点的左右子树有一个不是平衡树 2.该节点的左右子树都是是平衡树，但是把左右子树合并时，两个树的深度之差超过了1。当碰见这两种情况，都直接返回-1。
class Solution {
public:
bool isBalanced(TreeNode* root) {
return fun(root)!=-1;
}
int fun(TreeNode * node){
if(!node) return 0;
int left=fun(node->left),right=fun(node->right);
if(left==-1||right==-1||abs(left-right)>1) return -1;
return max(left,right)+1;
}
};😈重建二叉树——节点指针的赋值（剑指第7题）
当需要对二叉树的节点指针进行赋值时，一般采用带返回值的递归算法
输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
输入 : preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出 : [3,9,20,null,null,15,7]
首先要搞清楚前序遍历和中序遍历得到的数组的构成
前序遍历数组和中序遍历数组可以分割成一块一块的部分，每一块由根节点和它的左右子树构成。对于前序数组中的某个根节点，它的索引值为index，并且该根节点在中序数组中的索引值为temp，可以得到：
根节点的左节点在前序数组中的索引值为index+1，
而该节点右节点的索引值的求解就比较复杂，如果能知道当前根节点所构成的二叉树的左子树中节点的个数i，那么在前序遍历数组中根节点右节点的索引值为index+i+1，而在中序遍历数组中，左节点与右节点在根节点两边均匀分布，用left和right来表示在中序遍历数组中，当前根节点的最下面一层的左节点和右节点的索引值。则在前序遍历数组中，根节点的右节点的索引值为index+temp-left+1
对于这类节点指针的赋值，要注意对指针先初始化再赋值，即先new再进行赋值。类似于下面的代码是不正确的，需要先对temp->left进行初始化，才能继续后面的操作，所以递归操作采用了带返回值的函数。
Treenode * temp = new Treenode (0);
fun(temp->left);//错误 要先初始化
temp->left=new Treenode(1);
fun(temp->left);class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode * res=new TreeNode(0);
for (int i=0;i<inorder.size();i++) memory[inorder[i]]=i;
return fun(preorder,0,0,len-1);
}
TreeNode * fun(vector<int>& preorder,int index,int left,int right){
//left right表示的是当前根节点所拥有的最深的左右子节点在中序数组的下标
if(left>right) return NULL;
int temp=memory[preorder[index]];//对应数据在中序数组的下标
TreeNode * node = new TreeNode (preorder[index]);
node->left=fun(preorder,index+1,left,temp-1);
node->right=fun(preorder,index+temp-left+1,temp+1,right);
return node;
}
private:
unordered_map<int,int> memory;
};树的子结构（剑指26） 依旧是带返回值的递归算法
输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)，B是A的子结构， 即 A中有出现和B相同的结构和节点值。
例如:给定的树 A: 给定的树 B：
3 4
/ \ /
4 5 1
/ \
1 2
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。
此题要在二叉树A中寻找是否存在子二叉树B，解题的思路还是蛮常规的：遍历二叉树A的节点，如果某个二叉树A中的某个节点N等于二叉树B的根节点，那么就开始遍历二叉树B，判断该节点 N后续的节点是否与二叉树B相等。
由上面的分析可知，此题需要两次遍历，一次是遍历二叉树A，判断是否有节点等于二叉树B的根节点，如果存在相等的节点的话，就进入下一个遍历，判断后续的节点与二叉树B中的是否相同。
至于遍历顺序，采用前序遍历，按根节点，左子结点，右子节点的顺序来。
此题因为涉及到对多个节点值的判断，所以需要用到带返回值的递归函数。在书写时，先确定递归函数直接退出的条件，递归函数直接退出的情况有三个：
一个是当前遍历完二叉树B了，并且当前树的节点与二叉树B中的节点都相等（返回true），
一个是处于便利遍历的过程中，当前的节点与二叉树B中同样位置处的节点的值并不相等；
一个是当前二叉树A遍历完了，但还未完全找到与二叉树B相等的子树。
对应下面三种：
当节点 node_b 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true ；
当节点 node_a 为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false ；
当节点 node_a 和 node_b 的值不同：说明匹配失败，返回 false ；
至于其他不满足该条件的情况，就直接return加递归调用即可
class Solution {
private:
TreeNode * root_B;
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
root_B=B;
if(!B) return false;
return loop_a(A);
}
bool loop_a(TreeNode * node_a){
if(!node_a) return false;
if(node_a->val==root_B->val&&loop_b(node_a,root_B)) return true;
return (loop_a(node_a->left)||loop_a(node_a->right));
}
bool loop_b(TreeNode * node_a,TreeNode * node_b){
if(!node_b) return true;
if(!node_a) return false;
if(node_a->val!=node_b->val) return false;
return loop_b(node_a->left,node_b->left) && loop_b(node_a->right,node_b->right);
}
};关于带返回值的递归函数的一个注意点（以力扣226为例）
翻转一颗二叉树，将左右子树全部翻转。例子如下：
翻转前 4 / \ 2 7 / \ / \ 1 3 6 9翻转后 4 / \ 7 2 / \ / \ 9 6 3 1
代码如下，非常简单。但此段代码中有一个注意点：TreeNode * res=new TreeNode(root->val);
这一句是新建了一个val值与root节点一样的节点res，注意此处是另外新建的，所以res与root除了val值相等外没有任何联系，所以用TreeNode * res=root是错误的，这会使两个节点指针产生交叉，会影响后续的判断，
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(!root) return NULL;
TreeNode * res=new TreeNode(root->val);
res->left=mirrorTree(root->right);
res->right=mirrorTree(root->left);
return res;
}
};打家劫舍Ⅲ（第337题） DP与DFS的结合🐱🐉
在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。
简化下问题，问题的要求就是：一棵二叉树，树上的每个节点都有对应的值，问在不同时选中有父子关系的点的情况下，能选中的点和的最大值是多少。
一开始的想法是，采用层序遍历，将每一层的值的和存入一个数组中，然后求此数组中不相邻的元素的和的最大值。但这种方法具有局限性，没有将所有条件都考虑进去，如下
三层的节点的和分别是2 4 4，按上述方法得到的总和最大值为6，但实际上最大值为节点值3加节点4，为7。
所以需要思考其他方法，本题还是要采用动态规划法，设置两个动态数组unordered_map<<TreeNode*,int>steal和not_steal , 索引值为二叉树的节点地址。其中steal[node]表示如果当前节点的值计入总和，那么到目前节点为止，和的最大值。not_steal[node]表示如果当前节点的值不计入总和，那么到目前节点为止，和的最大值。
接下来推导动态方程：
若当前节点node的值计入总和的计算中，那么它的左右节点就不能计入总和的计算，所以到目前目前节点为止，总和的最大值为当前节点的值 node->val 加上左右子节点不计入总和时的值 not_steal[node->left] , not_steal[node->right]
若当前节点node的值不计入总和的计算中，那么它的左右子节点可以计入总和的计算，也可以不计入总和的计算。那么此时总和的最大值就是 max( steal[node->left], not_steal[node->left] ) + max( not_steal[node->right], steal[node->right] )
最后就是确定遍历的方式，此题中节点的遍历应该是由下到上，先确定到子节点的总和最大值，再计算父节点的，所以用后序遍历。
class Solution {
public:
unordered_map<TreeNode*,int> steal,not_steal;
int rob(TreeNode* root) {
dfs(root);
return max(steal[root],not_steal[root]);
}
void dfs(TreeNode * node){
if(!node) return;
dfs(node->left);
dfs(node->right);
steal[node] = node->val + not_steal[node->left] + not_steal[node->right];
not_steal[node] = max( steal[node->left], not_steal[node->left] )
+ max( not_steal[node->right], steal[node->right] );
}
};😈最近父节点（第236题）
给定一个二叉树, 找到该树中两个指定节点的最近公共父节点。
最近公共父节点的定义为：“对于有根树 T 的两个节点 p、q，最近公共父节点表示为一个节点 x，满足 x 是 p、q 的父节点且 x 的深度尽可能大（一个节点也可以是它自己的父节点）。”
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出：3
此题在递归过程中对于当前节点，可能会涉及到对其父节点/子节点的判断，所有应该采用带返回值的递归函数。
此处需要注意遍历的顺序的意义，对于后序遍历来说，对节点进行操作的顺序（如打印节点）为左子节点-》右子节点-》父节点，其实，前序，中序，后序遍历的区别在于对父节点进行操作的顺序的先后不同（分别是最先操作，在左子节点和右子节点中间，最后操作），也就对应着在遍历函数中，对当前节点进行操作的语句的放置位置。此处最先进行处理的应该是两个指定节点，然后才是他们上层的父节点，所以应该采用后序遍历的思路来编写程序。
具体解法：
根据以上定义，若 rootroot 是 p,q 的 最近公共父节点 ，则只可能为以下情况之一：
- p 和 q 在 rootroot 的子树中，且分列 rootroot 的 异侧（即分别在左、右子树中）；
- p = root，且 q 在 root 的左或右子树中；
- q = root，且 p 在 root 的左或右子树中；
关于遍历递归函数的编写：
最主要的是确定递归函数的作用和返回值的含义，本题中的递归函数的作用是寻找当前节点与等待寻找最近父节点的两个节点p与q的关系，并将关系通过返回值体现出来，如果返回的是空指针，代表p与q不再当前节点的子树上，如果返回值是非空，代表当前节点至少是p与q中的一个的父节点
终止条件：
当越过叶节点，则直接返回null ；
当 root等于 p,q ，则直接返回 root；
递推工作：
开启递归左子节点，返回值记为 left ；
开启递归右子节点，返回值记为 right；
返回值：
根据 left 和 right ，可展开为四种情况；
- 当 left 和 right 同时为空 ：说明 root 的左 / 右子树中都不包含 p,q ，返回 null ；
- 当left 和 right 同时不为空 ：说明 p,q 分列在 root 的 异侧 （分别在 左 / 右子树），因此 root 为最近公共祖先，返回 root ；
- 当 left 为空 ，right 不为空 ：p,q 都不在 root 的左子树中，直接返回 right。具体可分为两种情况：(1).q 其中一个在 root的 右子树 中，此时 right 指向 p（假设为 p ）；(2).p,q 两节点都在 root 的 右子树 中，此时的 right 指向 最近公共祖先节点 ；
- 当 left 不为空 ， right 为空 ：与情况 3. 同理；
|
|
|
|
|
|
对代码做一些说明：本题的思路就是由上至下遍历二叉树，找到对应的q和p后在按原路返回，并且在返回的过程中不断寻找最近父节点，这也符合后序遍历的流程
//父节点与子节点有一定关系 需要用带返回值的递归
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return the_father(root,p,q);
}
TreeNode * the_father(TreeNode * node,TreeNode* p, TreeNode* q){
//判断入口处的参数 若满足条件直接退出 接下来不会继续向下遍历 而是开始向上回溯
if(!node) return NULL;
if(node==p||node==q) return node;
//判断当前节点两个子节点的状态 根据不同状态返回不同值
TreeNode * left=the_father(node->left,p,q);
TreeNode * right=the_father(node->right,p,q);
if(!left&&!right) return NULL;
if(left&&right) return node;
if(left) return left;
return right;
}
};最近父节点的变形——搜索二叉树（剑指68题）
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。（一个节点也可以是它自己的祖先）。
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
这是一个二叉搜索树，所以当前节点的值大于其所有左子树节点的值，而小于其所有右子树结点的值，题目要求：找到该树中两个指定节点的最近公共祖先。这里就需要分情况讨论，首先从根节点开始找起；
如果两个结点的值一个比根节点（当前查找的结点）的值小，另一个比根节的值点大，则根节点就是两个指定节点的最近公共祖先。（递归出口）
如果两个结点的值都比根节点（当前查找的结点）的值小，则直接在该节点的左子树上寻找。
如果两个结点的值都比根节点（当前查找的结点）的值大，则直接在该节点的右子树上寻找。
class Solution {
public:
TreeNode* fun(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root) return root;
if(root->val<p->val&&root->val<q->val) return fun(root->right,p,q);
if(root->val>p->val&&root->val>q->val) return fun(root->left,p,q);
return root;
}
};序列化二叉树（剑指第37题）
请实现两个函数，分别用来序列化和反序列化二叉树。你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
即输入一个二叉树，将其序列化，转化为字符串，再将字符串反序列化，转化为二叉树输出，并且在序列化和反序列化的过程中，对与字符串的形式没有要求，只要最后能得到正确的二叉树即可。具体的函数调用如下所示：
Codec ser, deser; TreeNode* ans = deser.deserialize(ser.serialize(root));
输入：root = [1,2,3,null,null,4,5] 输出：[1,2,3,null,null,4,5]
观察题目示例，序列化的字符串实际上是二叉树的 “层序遍历”（BFS）结果，本文也采用层序遍历。为完整表示二叉树，考虑将叶节点下的 null 也记录。在此基础上，对于列表中任意某节点 node ，其左子节点 node.left 和右子节点 node.right 在序列中的位置都是唯一确定 的。如下图所示：
由二叉树构造字符串，很常规，用队列来辅助二叉树的层序遍历。而由字符串构建二叉树，则也要用到队列，不过这是建立在字符串中包含了叶子节点下面null节点信息的前提下。代码如下
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root==NULL) return "";
string the_string;
queue<TreeNode *> the_tree;
the_tree.push(root);
while( !the_tree.empty() ){
TreeNode * temp = the_tree.front();
the_tree.pop();
if(temp){
the_tree.push(temp->left);
the_tree.push(temp->right);
}
the_string.append(temp?to_string(temp->val)+",":"null,");
}
the_string.pop_back();
return the_string;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data=="") return NULL;
queue<TreeNode *> the_tree;
vector<string> the_data;
data.push_back(',');
the_data = splitString(data);
int index=1;
TreeNode * the_root = new TreeNode(stoi(the_data[0]));
the_tree.push(the_root);
while(!the_tree.empty()){
TreeNode * temp = the_tree.front();
the_tree.pop();
if(the_data[index]!="null"){
temp->left = new TreeNode(stoi(the_data[index]));
the_tree.push(temp->left);
}
index++;
if(the_data[index]!="null"){
temp->right = new TreeNode(stoi(the_data[index]));
the_tree.push(temp->right);
}
index++;
}
return the_root;
}
vector<string> splitString(string & data){
int begin=0,end=1;
vector<string> the_data;
while(end<data.length()){
while(end<data.length()&&data[end]!=',') end++;
the_data.push_back(data.substr(begin,end-begin));
begin=end+1;
end=begin+1;
}
return the_data;
}
};二叉树中的最大路径(力扣124题)
给你一个二叉树的根节点
root，返回其 最大路径和 。路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到树中另一个节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径至少包含一个 节点，且不一定经过根节点root，路径和是路径中各节点值的总和。
输入：root = [-10,9,20,null,null,15,7] 输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
此题需要用到递归的方法，关于二叉树的递归，有一个很重要的思想，就是要明确迭代函数的作用是什么，它对于当前节点做了什么处理，它要返回的是什么。
对于本题，迭代函数的作用是确定在包含当前节点的路径中，路径和的最大值，并将该最大值返回，迭代函数执行的顺序是从根节点向下一直到叶节点，接着开始回溯，逐个返回包含当前节点的路径和的最大值，将其用于上一层的判断。
因为在回溯过程中，当前的节点的值可能为负值，那么在此时计算路径和最大值中不应该包含该节点，然而为了函数正确回溯，函数的返回的值中需要包含当前节点，所以需要额外设置一个全局变量，在每次迭代过程中更新从回溯开始到现在的路径和的最大值。
用int ret来表示函数的返回值，用int midVal来表示全局变量。当函数回溯到某个节点 TreeNode * node时，这两个值的可能取值如下：
首先假设当前节点的左右子节点的迭代函数已经正确执行并且分别返回包含这两个子节点的路径和的最大值（这个假设是解决迭代函数问题的关键）。如果两个子节点的函数返回值中存在负数，那么在计算ret和midVal时当不应该考虑这些为负值的情况，即直接将子节点的返回值设为0。
ret是包含当前节点的路径和的最大值，有两个选择，当前节点的值加上左子结点的路径和最大值；或者当前节点加上右子节点的路径和最大值，在这两者之中取较大值。
midVal是在回溯过程中的路径和的最大值，如果当前节点的值node->val为负，那么可以直接不考虑包含当前节点的路径和的最大值。具体的计算方式就是计算上一个midVal和以当前节点为根节点的路径和中的较大值。
class Solution {
public:
int midVal = INT_MIN;//midval指的是当前最大路径值
int maxPathSum(TreeNode* root)
{
findMaxPath(root);
return midVal;
}
int findMaxPath(TreeNode * node){//返回值指的是返回经过该节点的单边的最大值
if (!node) return 0;
int left = max(findMaxPath(node->left), 0);
int right = max(findMaxPath(node->right), 0);
midVal = max(node -> val + left + right, midVal);
int ret = max(left, right) + node -> val;
return ret;
}
};链表
环形链表（第142题）
一般链表问题都是用双指针法来解决，如寻找找距离尾部第K个节点（上文双指针一节有提到）、寻找环入口、寻找公共尾部入口等。
给定一个链表，判断该链表是否含有环形链表，若包含，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。 说明：不允许修改给定的链表
为了表示给定链表中的环，使用整数 pos 来标识入环点的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于控制台输入时，标识环的位置，并不会作为参数传递到函数中。
输入：head = [3,2,0,-4], pos = 1 输出：返回索引为 1 的链表节点 解释：链表中有一个环，其尾部连接到第二个节点。
对于环形链表，通常用双指针来解题，对于此题可以 设置两个快慢指针，将问题转变为快慢指针的追赶问题。如下图，
快慢指针 fast 和 slow 起初位于头结点，随后 fast 指针每次前进两个节点，slow 指针每次前进一个节点。
如果该链表不包含环形链表，则 fast 的值或 fast->next 的值会变成NULL，则退出并返回NULL
如果该链表包含环形链表，则 fast 和 slow 两者都会进入环内，并且开始循环前进，而 fast 前进的速度快于 slow，可知最终 fast 会追赶上slow。
下面开始分析两节点走过的路程：
- 可以认为从开始到第一次相遇，fast 和 slow前进的次数是相同的。而 fast 一次前进的距离是 slow 的两倍，可得
。并且 fast 与 slow 在环内相遇，fast 与 slow 重复走过的路径就是这个环形链表，可以认为 fast 在相遇时比 slow 多走的路程为
，其中b为环形链表的节点个数，而n为正整数，与链表的结构有关，所以可得
。与上式联立可得
。可以得出相遇时两节点走过的路程。
- 对于环形链表的入口节点。可以将其指针到达该节点的路程表示为
，i为在环形链表表内循环的次数。当两指针第一次相遇时，慢指针 slow 走过的总路程为
步即可。
- 而注意到，从链表头节点到环形链表的入口节点，所需要走过的路程为
|
|
|
|
|
|
代码如下:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * fast=head;
ListNode * low=head;
if (!head) return NULL;
while(true){
if(!fast) return NULL;
fast=fast->next;
if(!fast) return NULL;
fast=fast->next;
low=low->next;
if(fast==low) {
fast=head;
break;
}
}
while(fast!=low){
fast=fast->next;
low=low->next;
}
return low;
}
};😈LRU缓存的实现（第146题）
运用你所掌握的数据结构，设计和实现一个 LRU缓存机制 。
LRUCache 类的类内函数：
- LRUCache(int capacity) ：以正整数作为容量 capacity 初始化 LRU 缓存
- int get(int key) ：如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
- void put(int key, int value) ：如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用（即未被get(),put()两函数调用）的数据值，从而为新的数据值留出空间。
要求在
O(1)时间复杂度内完成上述操作。
输入：["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出： [null, null, null, 1, null, -1, null, -1, 3, 4]解释：
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
要求get操作时时间复杂度为1，即查找的时间复杂度为1，考虑使用哈希表。
要求put时间复杂度为1，即插入操作时间复杂度为1，并且当存储空间满了的时候，将最久没有处理数据弹出，即应该满足先进先出原则，考虑使用队列，但是存储空间中元素的先后顺序并不是一成不变的，当进行get操作对某些元素进行查询时，会改变缓存中数据的先后操作顺序，需要相应的对其中数据顺序进行调整，而此调整要求时间复杂度也为1，而对于队列来说，无法在时间复杂度为1的情况下对其中的任意两数据进行位置的调整，顺序存储结构在此处不适用，所以只能使用链表进行操作。
由题意，put 和 get 方法的时间复杂度需为 O(1)，可以看出这个数据结构 cache 必要的条件：查找快，插入快，删除快，有顺序之分。
- 因为显然 cache 必须有顺序之分，以区分最近使用的和久未使用的数据；而且我们要在 cache 中查找键是否已存在；如果容量满了要删除最后一个数据；每次访问还要把数据插入到队头。
- 最先想到的数据结构是哈希表map，哈希表查找快，可以满足时间复杂度为O(1)的要求，但是哈希表无法依据处理的先后顺序更新其中数据。
- 所以本题的关键是再找到一种数据结构，它有先进先出的特点，并且能够快速的将其中的某个数据移动到该数据结构的末尾，移动的时间复杂度为O(1)。可以考虑双向链表来实现。
- 将上述两种数据结构结合，形成一种新的数据结构：哈希链表，哈希表中存储key以及在链表中存储key值的节点地址，哈希表内的key值不需要排序，双向链表的节点中存储key值和对应的value值，链表中节点按先入先出的顺序插入。
| 哈希表 | 插入到头结点之后 | 删除尾节点之前的 | 将原本的节点删除 | ||
| 已存在 该节点 | 满 | 更新 | √ | - | √ |
| 未满 | 更新 | √ | - | √ | |
| 不存在该结点 | 满 | 插入新值 删除旧值 | √ | √ | - |
| 未满 | 插入新值 | √ | - | - |
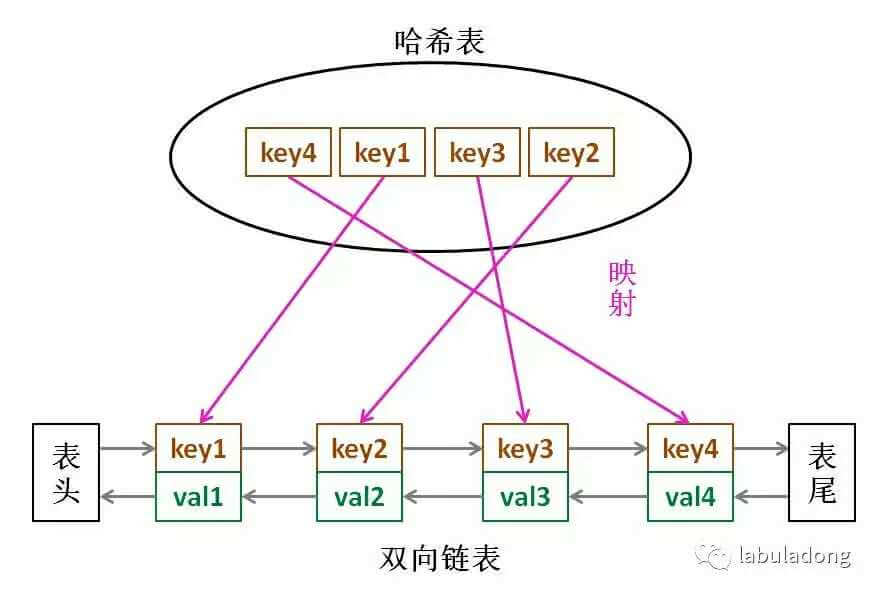
class LRUCache {
public:
struct node{
node * next;
node * last;
int val,key;
node() {next = NULL; last = NULL;}
node(int num1, int num2) {key = num1; val = num2; next = NULL; last = NULL;}
}* head, * tail;
unordered_map<int, node*> memory;
int maxsize;
LRUCache(int capacity) {
maxsize = capacity;
head = new node;
tail = new node;
head -> next = tail;
tail -> last = head;
}
int get(int key) {
if(memory.find(key) != memory.end()){ //存在
deletenode(memory[key]);
addnodetohead(memory[key]);
return memory[key] -> val;
}
else return -1;
}
void put(int key, int value) {
if(memory.find(key) != memory.end()) { //存在
deletenode(memory[key]);
memory[key] -> val = value;
addnodetohead(memory[key]);
}
else {
if(memory.size() == maxsize){
memory.erase(tail -> last -> key);
deletenode(tail -> last);
}
memory[key] = new node(key, value);
addnodetohead(memory[key]);
}
}
void deletenode(node * mid){ //删除中间节点
(mid -> last) -> next = mid -> next;
(mid -> next) -> last = mid -> last;
}
void addnodetohead(node * temp){ //加入节点到头结点之后
(head -> next) -> last = temp;
temp -> next = head -> next;
head -> next = temp;
temp -> last = head;
}
};😈😈链表排序（第148题） 📢重点⭐
给你链表的头结点 head ，请将其按升序排列并返回排序后的链表 。要求在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。
输入：head = [-1,5,3,4,0]输出：[-1,0,3,4,5]
由于题目要求空间复杂度是 O(1)，因此不能使用递归。因此这里使用 bottom-to-up 的算法来解决。两个两个的 merge，完成一趟后，再 4 个4个的 merge，直到结束。
主要用到两个比较重要的函数：merge()函数和cut()函数，分别用于合并有序链表以及切割链表，应当记住其书写方式。
/*current = dummy.next;
tail = dummy;
for (step = 1; step < length; step *= 2) {
while (current) {
// left->@->@->@->@->@->@->null
left = current;
// left->@->@->null right->@->@->@->@->null
right = cut(current, step); // 将 current 切掉前 step 个头切下来。
// left->@->@->null right->@->@->null current->@->@->null
current = cut(right, step); // 将 right 切掉前 step 个头切下来。
// dummy.next -> @->@->@->@->null，最后一个节点是 tail，始终记录
// ^
// tail
tail.next = merge(left, right);
while (tail->next) tail = tail->next; // 保持 tail 为尾部
}
}*/class Solution {
public:
ListNode* sortList(ListNode* head) {
ListNode * dummyHead=new ListNode(0);
dummyHead->next = head;//虚拟头节点,用于存储头节点，
auto p = head;//p作为临时变量
int length = 0;
while (p) {
++length;
p = p->next;
}
delete p;
// dummyHead->head->@->@->@->@->@->@->@->@->@...
for (int size = 1; size < length; size<<=1) {
//给两个指针变量赋初值
auto cur = dummyHead->next;//注意：此处等号右端不能写成head，因为经过排序，
//dummyHead的next节点已经发生了变化，不是原来的head
auto tail = dummyHead; //tail变量用于将排好序的链表连接在一起
while (cur) {
auto left = cur;
auto right = cut(left, size); // left->@->NULL right->@->@->@...
cur = cut(right, size); // left->@->NULL right->@->NULL cur->@->...
tail->next = merge(left, right);//合并成有序链表
while (tail->next) {
tail = tail->next;
}//tail此时位于排好序的链表的尾节点
}
}
return dummyHead->next;
}
//将链表进行切割，切掉包含头节点在内的n个节点，返回在原链表中第n个节点(即此新链表的尾节点)
//的下一个节点地址，作为后续操作的头节点,并且将新链表的尾节点的下一个节点置为NULL，以达到
//分割的效果
ListNode* cut(ListNode* head, int n) {
auto p = head;//也是做临时变量
while (n>1 && p) {//此处n的边界值，可以用n=1来确定，n=1时，不用进入循环
p = p->next;
n--;
}
//退出while循环有两钟情况:p节点为空;已经切割完n个节点
//下面这种写法比if(n>1)要好，因为能把p为空指针的情况先排除掉
if (!p) return nullptr;//如果p为空节点 返回空指针
auto next = p->next;//将p节点的下一个节点地址作为返回值
p->next = nullptr; //实现分割,与后续的节点没有关系
return next;
}
ListNode* merge(ListNode* l1, ListNode* l2) {//合并两个有序链表为一个有序链表，
//返回合并后链表的头节点，参考归并排序
auto dummyHead = new ListNode(0);//设置一个伪头节点，用以存储实际的头节点
auto p = dummyHead;
while (l1 && l2) {//循环停止的条件为l1或l2链表遍历到尾部
if (l1->val < l2->val) {
p->next = l1;
l1 = l1->next;
} else {
p->next = l2;
l2 = l2->next;
}
p=p->next;
}
//如果出现l1->@->@;l2->@->@->@->@的情况，上述循环在l1的尾节点停止，
//此时需要把l2链表剩下的节点直接加在目标链表后
p->next = l1 ? l1 : l2;//将l1或l2剩下的链表加到后面
return dummyHead->next;
}
};😈相交链表（第160题🐱👤带文豪出没）
给你两个单链表的头节点
headA和headB，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回null。如下，应返回C1节点
一般的解法是构造一个哈希表，遍历两个链表，将节点存入哈希中，如果哈希表存在重复插入的现象，则说明有公共节点。
但对于链表问题，一般都可以用双指针法来解决，难点是如何确定双指针的前进方式以及如何令两指针相遇。
对于此题，设两个指针node_a,node_b的起点为a1 b1，希望两个指针在c1处相遇，然而从起点到c1的距离并不相等，应当设计一种路径，使两指针在c1相遇时走过的路相同，注意到从a1到c1的距离不等于从b1到c1的距离，那么让node_a,node_b将这两段距离都走一下，这样在相遇时，走过的路程就一样了。
具体的路程如下：
node_a: a1->a2->c1->c2->c3->b1->b2->b3->c1
node_b: b1->b2->b3->c1->c2->c3->a1->a2->c1
通俗点说就是：走到尽头见不到你，于是走过你来时的路，等到相遇时才发现，你也走过我来时的路。
如果两个链表不相交，那么node_a,nde_b到对方的链表上后，最后会一起等于NULL。
代码如下：
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(!headA||!headB) return NULL;
ListNode * node_a = headA;
ListNode * node_b = headB;
while(node_a!=node_b){
node_a=(node_a?node_a->next:headB);
node_b=(node_b?node_b->next:headA);
}
return node_a;
}
};😈反转链表（第206题 重点🐱🚀对于指针赋值操作的书写锻炼）
给你单链表的头节点
head，请你反转链表，并返回反转后的链表
简单来说，此题就是给出一组数据，按顺序将其插入到链表的尾部。若ptr表示要返回的指针，temp表示存储数据的节点，在循环中执行以下语句即可。
temp -> val = num;
temp -> next = ptr;
ptr = temp;
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode * curr=head;
ListNode * pre=NULL;
while(curr){
ListNode * temp = curr->next;
//这一句和下面第四句的作用是将curr->next保护起来，防止第二三句改变其原本的数据
curr->next=pre;
pre=curr;
curr=temp;
}
return pre;
}
};关于链表中指针的操作，当出现->next 的赋值时 需要注意 指针后续的指向，上面代码中，实现的功能是将pre和curr指针顺次向后移，注意到while语句中，指针的赋值构成了一个循环。
假设构造了一个链表，开头元素为head 链表中元素为：1->2->3->4，下面的程序将输出0，而不是3。因为temp接在了head的后面，那么原本head后面的元素都将改变。
int main(){
ListNode * temp =new ListNode;
ListNode * pre =new ListNode(0);
temp=head->next;
temp->next=pre;
cout<<head->next->next->val<<endl;
return 0;
}解法二：递归法
此题的递归法有一些些的不同，此题是要先遍历链表直到尾部，接着从尾部开始回溯，当到达尾部后，返回值res就确定下来了——链表的最后一个元素，并且在后续的回溯过程中，res值也保持不变，会变化的是链表不同元素之间的指向。
对于head->next->next=head一句，需要做一些说明，例如对于链表 head->head1->head2，执行上面语句达到的效果就是将head后一个元素的再后一个的指向改变为head本身，执行完之后上述链表变为head->head1->head，接着再执行head->next=NULL，上述链表变为head1->head->NULL，实现了链表的反转。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head||!head->next) return head;
ListNode * res=reverseList(head->next);
head->next->next=head;
head->next=NULL;
return res;
}
};二叉搜索树与双向链表（剑指第36题）
输入一棵二叉搜索树，将该二叉搜索树转换成一个由小到大有序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继（即节点左指针要指向第一个小于它的节点，节点的右指针要指向第一个大于它的节点）。还需要返回链表中的第一个节点的指针。
例如上述二叉树，需要调整其五个节点的指针的指向，使得生成的链表中的元素由小到大排列，并且节点的左指针指向比它小的元素，节点的右指针指向比它大的元素。
本题考察的是二叉搜索树的性质，二叉搜索树中序遍历得到的数组是有序的，所以此题的基本思路就是，对二叉搜索树进行中序遍历，在中序遍历的过程中改变节点left和right指针的指向。
在中序遍历的过程中，函数从根节点进入并向下遍历，但最先进行处理的节点是最左下角的节点，并且此节点的值也是整个二叉搜索树中最小的，接着回溯，处理的是它的父节点，此父节点的值是二叉树转化成的有序数组中紧挨着最左下角节点的值。所以所以可以的出一个结论：在进行中序遍历的回溯过程中（即遍历到了尽头，开始由下向上返回），上一个循环的节点值before，恰好小于当前节点值now。即now->left=before before->right=now；
class Solution {
private:
Node * head=NULL,* before=NULL;//before用于存储上一次递归的节点指针
public:
Node* treeToDoublyList(Node* root) {
if(!root) return root;
fun(root);
head->left=before;//将链表的头尾元素建立联系
before->right=head;
return head;
}
void fun(Node * now){
if(!now) return;
fun(now->left);
if(before) before->right=now;//第一次执行该句时，函数到达最左下角节点并开始回溯
else head=now;
now->left=before;
before=now;
fun(now->right);
}//当递归函数退出后 before存储的是搜索二叉树最右下角的值
};合并k个有序链表（力扣23题）
给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。
输入：lists = [[1,4,5],[1,3,4],[2,6]] 输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[ 1->4->5, 1->3->4, 2->6 ]
将它们合并到一个有序链表中得到：1->1->2->3->4->4->5->6
最直观的做法，建立一个优先队列，然后将链表中所有节点的值都填入，之后重新构造一个链表，将优先队列中的值重新填入，难点在于优先队列中，出队元素是由大到小的，所以在重新构建一个升序的链表时会有一些困难。
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
priority_queue<int> q;
for (auto node : lists) {
while (node) {
q.push(t->val);
node = node->next;
}
}
ListNode *res = NULL;
while (!q.empty()) {
ListNode *p = new ListNode(q.top());
q.pop();
p->next = res;
res = p;
}
return res;
}
};
堆与priority_queue
数组中的第k个最大元素：堆排序 ⭐面试常考（第215题）
给定整数数组
nums和整数k，请返回数组中第k个最大的元素。请注意，你需要找的是数组排序后的第k个最大的元素，而不是第k个不同的元素。输入: [3,2,3,1,2,4,5,5,6] 和 k = 4 输出: 4
堆排序算法 堆排序算法_#时代不杀菜鸡#的博客-CSDN博客
法一：
构建最小堆，维护堆的元素个数为k个。
//最小树
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
for(int i=0;i<k;i++){
shiftup(nums,i); //用数组的前k个元素先构建出一个长度为k的最小堆
}
for(int i=k;i<nums.size();i++){
if(nums[i]>nums[0]){
swap(nums[i],nums[0]);//如果后续的点大于最小堆的顶点，替换并执行下沉函数
shitfdown(nums,0,k-1);
}
}
return nums[0];//堆的顶点值就是第k大的元素
}
void shiftup(vector<int> & nums, int index){//上浮操作
while(index>0){
int father = (index-1)/2;
if(nums[father]>nums[index]){
swap(nums[father],nums[index]);
index=father;
}
else break;
}
}
void shitfdown(vector<int> & nums, int index, int edge){//下沉操作
while(index*2+1<=edge){
int left=index*2+1;
if(left+1<=edge){ //如果右子节点存在
int smaller=nums[left+1]>nums[left]?left:left+1; //两子节点中较小值的索引值
if(nums[smaller]<nums[index]) {
swap(nums[smaller],nums[index]);
index=smaller;
}
else break;//退出上面的while循环语句，关键一句，如果缺少，会陷入死循环
}
else if(nums[left]<nums[index]){//如果右子节点不存在
swap(nums[left],nums[index]);
index=left;
}
else break;
}
}
};法二：运用快速排序中的分段思想，设置哨兵，并将数组分为两部分，一边是比哨兵大的，另一边是比哨兵小的。不断分段进行排序，此外此题无需对整个数组排序，只要哨兵在分好段的数组中的索引值为nums.size() - k就可以停止运行。并且为了简化计算过程，在每次排序的开始，将队首元素与数组中的任一数据交换位置，接着将数组的第一个元素作为哨兵，以防止出现数组是逆序数组这样的极端情况。代码如下：
class Solution {
public:
int res;
int findKthLargest(vector<int>& nums, int k) {
res = nums.size() - k;
fun(nums, 0, nums.size() - 1);
return nums[res];
}
void fun(vector<int>& nums, int left, int right){
if(left >= right) return;
int temp = (left + right)/2 ;
swap(nums[left], nums[temp]);
int target = nums[left];
int i = left, j = right;
while (i < j){
while(i < j && nums[j] >= target) j--;
while(i < j && nums[i] <= target) i++;
swap(nums[i],nums[j]);
}
swap(nums[left], nums[i]);
if(i > res) fun(nums, left, i - 1);
else if(i < res) fun(nums, i + 1, right);
else return;
}
};数据流中的中位数（剑指41题）
定义中位数：如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。例如 [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构：
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。输入：
["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]
此题所要求的是一组数据中，大小位于中间的一个数值，需要设计一个数据结构，它能在插入新的数据时，对原有的数据流进行重新排序，并且能够找到数据流中的中位数。
我的做法是维护一个vector，vector中的数据有序，每当有新的数字插入时，用二分法查找数组中第一个小于该值的元素的下标，找到下标之后，用insert函数来将带插入数值插入到下标后一位上。因为vector对于中间值的插入操作耗时较长，所以该法效率较低。
进一步分析，可以把数组分成两个部分，两个部分中元素都有序，并且两部分元素个数相等或只相差一个，左边部分的值始终小于右边部分的值。这样在求中位数时，只需要知道左边部分的最大值和右边部分的最小值即可，即我们只关心这两个元素，至于两部分中数组如何排序则不关心。因此联想到用两个堆来实现。
建立一个 小顶堆 rightBoot 和 大顶堆 leftBoot ，分别保存列表左右两部分元素。
当要向左堆中插入数据时，为了保证左堆中的数据始终小于右堆中的，应该把待插入数据先放到右堆中“洗礼”，接着将右堆的堆顶元素弹出并插入到左堆中，这样就能保证左堆中的元素之中小于右堆中，对右堆进行元素的插入也是如此。
谈论完两个堆的插入策略后，应该确定元素的插入时机，在本题中，元素优先插入左堆中，在插入前检查两个堆的元素数量，当两个堆的元素数量相同时，将元素插入左堆，当两个堆的元素数量不同时，此时左堆比右堆多一个，则将元素插入右堆。这样的话，在确定中位数时，只需要在两个堆的堆顶元素汇总做选择即可。
确定中位数时，当两个堆的元素数量相同时，中位数为两个堆顶元素相加除以二，当两个堆的元素数量不同，中位数为左堆的堆顶元素。
class MedianFinder {
public:
priority_queue<int,vector<int>,greater<int>> rightRoot;//小顶堆 存储右边的数据
priority_queue<int,vector<int>,less<int>> leftRoot;//大顶堆 存储左边的数据
/** initialize your data structure here. */
MedianFinder() {}
void addNum(int num) {
//在此题中，设置 当两个堆中元素数量相同时，将新元素插入存储左边数据的堆中
// 当两个堆中元素数量不同时，此时左边比右边多，将新元素插入存储右边数据的堆中
if(rightRoot.size()==leftRoot.size()){
rightRoot.push(num);
leftRoot.push(rightRoot.top());
rightRoot.pop();
}
else{
leftRoot.push(num);
rightRoot.push(leftRoot.top());
leftRoot.pop();
}
}
double findMedian() {
if(rightRoot.size()==leftRoot.size()) return (double)(leftRoot.top()+rightRoot.top())/2;
else return leftRoot.top();
}
};😈😈队列的最大值（剑指59- Ⅱ）
请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。若队列为空，pop_front 和 max_value 需要返回 -1
对于普通队列，入队 push_back() 和出队 pop_front() 的时间复杂度均为 O(1) ；本题难点为实现查找最大值 max_value() 的 O(1) 时间复杂度。最直观的想法是：维护一个最大值变量 ，在元素入队时更新此变量即可；但当最大值出队后，并无法确定下一个次最大值 ，因此不可行。
所以本题解题的数据结构基础是一个队列，而重点是在队列压入和弹出时，如何更新其中的最大值。
之前求一个动态数组中的最大值，用的是栈的数据结构，不过那种情况适用于数组的起点确定，而终点元素动态变化的情况。此题中数组的起点元素和终点元素都是动态变化的，所以不能用栈的数据结构。相应的，用双端队列来实现
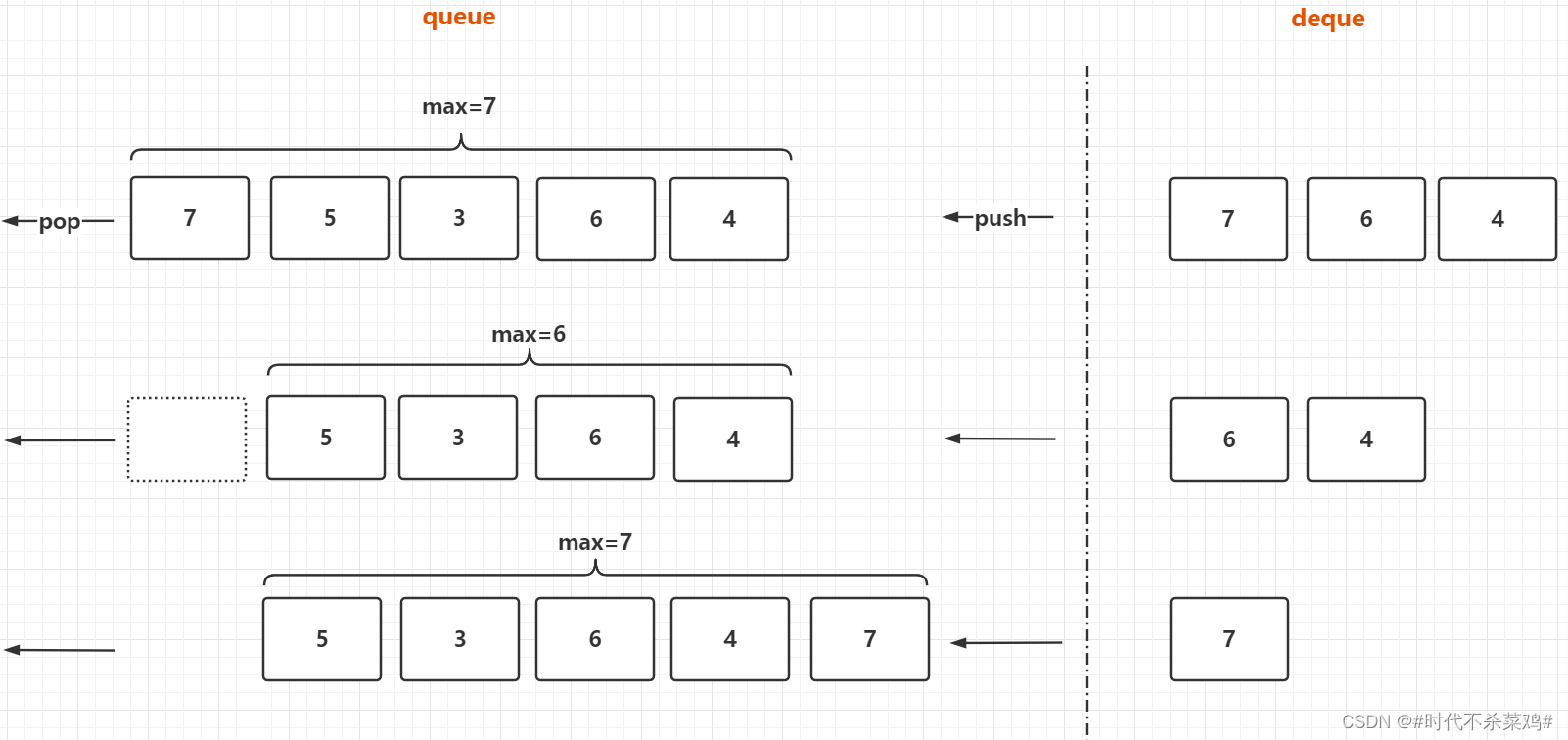由于队列先进先出的特性，当执行完pop()和push()操作后，队列的最大值总要在剩下的元素中进行更新，而进行push操作时，如果当前插入数字比它前面n个元素都要大，则将前面n个元素的最大值更新为当前插入值，即在求队列的最大值时，某个元素所能辐射到的区域是从它自身到前面第一个大于它的元素之间的区域。如果当前插入元素是最小值，则不做操作。当执行pop操作时，如果队首元素是当前队列的最大值，则弹出后队列的最大值要更新为它的下一个最大值。
所以需要再构建一个数据结构，该数据结构中，按大小存放队列的不同区域（起点都是队尾元素，终点不同）的最大值。用双端队列deque来实现。
代码如下：
class MaxQueue {
private:
queue<int> qe;
deque<int> de;
public:
MaxQueue() {}
int max_value() {
return qe.empty()?-1:de.front();
}
void push_back(int value) {
qe.push(value);
while(!de.empty()&&value>de.back()) de.pop_back();
de.push_back(value);
}
int pop_front() {
if(qe.empty()) return -1;
int temp=qe.front();
qe.pop();
if(temp==de.front()) de.pop_front();
return temp;
}
};😈滑动窗口的最大值（剑指59Ⅰ）
给定一个数组
nums和滑动窗口的大小k，请找出所有滑动窗口里的最大值。输入: nums = [1,3,-1,-3,5,3,6,7], k = 3 输出: [3,3,5,5,6,7]
此题的难点在于滑动窗口前移的过程中，不仅要将滑动窗口前一个元素加入滑动窗口，还要将滑动窗口最后一个数弹出，所以如何在弹出和压入数据的过程中维护滑动窗口的最大值，是本题的关键。与上题类似，构造一个长度为k的队列，用于充当滑动窗口，同时构造一个双端队列，用来存储滑动窗口中最大值的情况。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> res;
if(nums.size() == 0) return res;
deque<int> de;//存放最大值
queue<int> qe;//存放窗口值
de.push_back(nums[0]);
qe.push(nums[0]);
for(int i=1;i<k;i++) {
qe.push(nums[i]);
while(!de.empty() && nums[i]>de.back()) de.pop_back();
de.push_back(nums[i]);
}//构造长度为k的队列
res.push_back(de.front());
for(int i=k;i<nums.size();i++){//向队列中进行元素的插入和弹出
qe.push(nums[i]);
while(!de.empty() && nums[i]>de.back()) de.pop_back();
de.push_back(nums[i]);
if(qe.front() == de.front()) de.pop_front();
qe.pop();
res.push_back(de.front());
}
return res;
}
};栈问题——老大难（第20题）
这类问题往往比较难以想到用栈的解法，换句话说，就是难以将题目的条件与先入后出这个特性结合起来。
第20题
给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。
有效字符串需满足：左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。
示例1：输入：s = "{[]}" 输出：true 示例2：输入：s = "([)]" 输出：false
由题解可以看出，对于“（[）] ” 这样的字符串，是不符合题目要求的，原因在于两个小括号（）内没有完整的中括号，更具体的说，是“ [） ”这样的表达方式不合法，概括来说，对于一组长度不为0的连续的左括号字符串（类似于“ { ( [ ”）,紧接在其后的第一个右括号应当与最后一个左括号配对，后面的右括号，也应该按照左括号出现的由后到先的顺序，进行匹配。本题的栈专门用于存储左括号，这是本题的解题关键。
也就是说，字符串中的左括号入栈时，遵循先入后出的原则，更准确的说应该是先入的后消除原则：
当遍历字符串中的元素遇到右括号时，优先与栈顶的左括号进行匹配消除，
- 若遍历到右括号时，栈中没有元素，证明字符串中存在落单的右括号字符，返回false；
- 若两个括号无法组成一对，证明出错，返回false；
- 若两个括号能组成一对，那么将对应的左括号从栈中弹出；
- 当遍历完字符数组后，栈中还有元素剩下，证明还有落单的左字符，返回false
有两种写法：
class Solution {
public:
bool isValid(string s) {
unordered_map<char,int> m { {'(',1} , {'[',2} , {'{',3} ,
{')',4} , {']',5} , {'}',6} };
stack<char> st;
for(char c:s){
int flag=m[c];
if(flag>=1&&flag<=3) st.push(c);
else if(!st.empty()&&m[st.top()]==flag-3) st.pop();
else return false;
}
if(!st.empty()) return false;
return true;
}
};
class Solution {
public:
bool isValid(string s) {
if(s.empty()) return true;
stack<char> stack;
for(char c:s){
if(c=='(') stack.push(')');
else if(c=='{') stack.push('}');
else if(c=='[') stack.push(']');
else{
if(stack.empty()) return false;
char temp=stack.top();
stack.pop();
if(c!=temp) return false;
}
}
if(stack.empty()) return true;
return false;
}
};字符串
前缀树/字典树（第208题）
实现一种前缀树，用于高效地存储和检索字符串数据集中的键。几个关键函数：
- Trie() 初始化前缀树对象。
- void insert(String word) 向前缀树中插入字符串 word 。
- boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。
只保存小写字符的前缀树是一种特殊的多叉树，前缀树的每个节点TrieNode都存储着两个数据：
- bool型数据is_end：表示从根节点到当前节点为止，该路径是否形成了一个有效的字符串。
- 存储TrieNode *的vector数组children ：大小为 26 ，分别对应了26个英文字符 'a' ~ 'z'，如果children[i]的值不为空指针，代表着下一个节点存储的字母为a+i。
前缀树中比较关键的数据结构，是每个节点中存储的vector数组 vector<TrieNode *> children，数组里面的值为nullptr或一个TrieNode的指针。
每个节点代表一个字母，若某节点中的children数组中存储的都是nullptr，表示该节点后续没有其他节点了，意思是该节点表示的字母是最后字符串内的最后一个。
若某节点中的children数组中下标为i的位置存储着一个TrieNode的指针ptr，表示该节点链接到的下一个节点地址为ptr，意思就是在字符串中，该节点表示的字母后面还有字母，下一个字母为a+i。
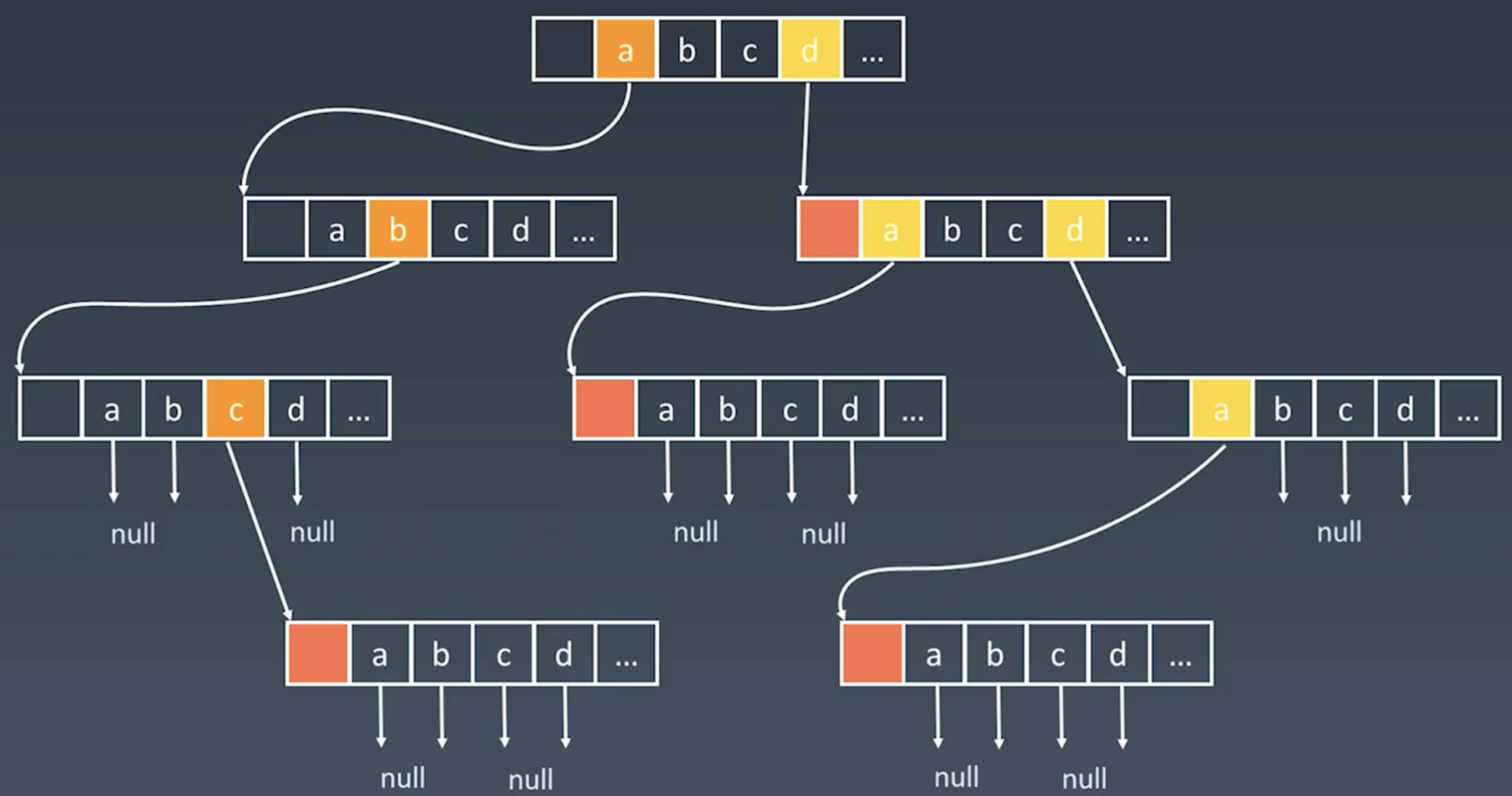
class Trie {
public:
class TrieNode{
public:
bool is_end=false;
vector<TrieNode *> children;
TrieNode ():children(26,nullptr) {}
};//前缀树的每个节点的信息
TrieNode *root = new TrieNode();//新建一个根节点
Trie() {}
//按照word的字符，从根节点开始，一直向下走
//如果遇到null，就new出新节点；如果节点已经存在，cur顺着往下走即可
void insert(string word) {
TrieNode * cur = root;
for(int i=0;i<word.size();i++){
int index=word[i]-'a';
if(!cur->children[index]) cur->children[index] = new TrieNode;
cur=cur->children[index];
}
cur->is_end=true;// 一个单词插入完毕，此时cur指向的节点即为一个单词的结尾
}
bool search(string word) {
TrieNode * cur = root;
for(int i=0;i<word.size();i++){
int index=word[i]-'a';
if(!cur->children[index]) return false;
cur=cur->children[index];
}
return cur->is_end;//按照word顺利的走完，判断此时cur是否为单词尾端
}
bool startsWith(string prefix) {
TrieNode * cur = root;
for(int i=0;i<prefix.size();i++){
int index=prefix[i]-'a';
if(!cur->children[index]) return false;
cur=cur->children[index];
}
return true;//如果顺利走完，直接返回true即可，不必关心此时cur是不是末尾
}
};字符串替换空格（剑指offer第5题）
请实现一个函数，把字符串 s 中的每个空格替换成"%20"。
输入：s = "We are happy." 输出："We%20are%20happy."
将字符串看作数组，空格是一个元素，而 "%20" 则是三个元素，新建一个字符串，遍历字符串s，在遍历过程中不断将元素填入。
class Solution {
public:
string replaceSpace(string s) {
string res;
for(int i=0;i<s.size();i++){
if(s[i]==' ') res+="%20";
else res+=s[i];
}
return res;
}
};
左旋转字符串 (剑指58-II)
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。
输入: s = "abcdefg", k = 2 输出: "cdefgab"
将前k个字符移动到字符串的末尾，有两种办法：
第一种最直观，就是将前k个字符依次移动到字符串的后面。
class Solution {
public:
string reverseLeftWords(string s, int n) {
for(int i=0;i<n;i++){
s.push_back(s[i]);
}
s.erase(0,n);
return s;
}
};
第二种，采用翻转部分字符串的方法来完成，比较巧妙
class Solution {
public:
string reverseLeftWords(string s, int n) {
reverse(s.begin(),s.begin()+n);
reverse(s.begin()+n,s.end());
reverse(s.begin(),s.end());
return s;
}
};正则表达式匹配（剑指19题）
请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配
输入：s = "aab" p = "c*a*b" 输出: true
本题中字符串 s 与 p 的长度不一定相等，或者说 s 与 p 内的字符不是一一递增对应的。设s的长度为n， p的长度为 m；将s的第i个字符记为 s_i，p 的第j个字符记为 p_j，将 s 的前i个字符组成的子字符串记为 s[:i] ，同理将 p 的前j个字符组成的子字符串记为 p[:j] 。因此，本题可转化为求 s [:n] 是否能和 p[:m] 匹配。总体思路是从 s[:1] 和 p[:1] 是否能匹配开始判断，每轮添加一个字符并判断是否能匹配，直至添加完整个字符串 s 和 p 。需要用到动态规划法
本题的状态共有 m×n 种，应定义状态矩阵 dp ，dp[i][j] 代表 s[:i]s[:i] 与 p[:j]p[:j] 是否可以匹配。
做好状态定义，接下来就是根据 「普通字符」 , 「.」 , 「*」三种字符的功能定义，分析出动态规划的转移方程。
状态定义： 设动态规划矩阵 dp ， dp[i][j] 代表字符串 s 的前 i 个字符和 p 的前 j 个字符能否匹配。
需要注意，在本题中，在两个字符串的头部再插入一个空字符，以防止后面遍历时发生越界。 dp[0][0] 代表的是空字符的状态， 因此 dp[i][j] 对应的添加字符是 s[i - 1] 和 p[j - 1] 。
当 p[j - 1] = '*' 时， dp[i][j] 在当以下任一情况为true 时等于true ：
dp[i][j - 2]： 即将字符组合 p[j - 2] * 看作出现 0 次时，能否匹配；
dp[i - 1][j] 且 s[i - 1] = p[j - 2]: 即让字符 p[j - 2] 多出现 1 次时，能否匹配；
dp[i - 1][j] 且 p[j - 2] = '.': 即让字符 '.' 多出现 1 次时，能否匹配；
当 p[j - 1] != '*' 时， dp[i][j] 在当以下任一情况为true 时等于rue ：dp[i - 1][j - 1] 且 s[i - 1] = p[j - 1]：
dp[i - 1][j - 1] 且 p[j - 1] = '.'：
初始化： 需要先初始化 dp 矩阵首行，以避免状态转移时索引越界。
dp[0][0] = true： 代表两个空字符串能够匹配。
dp[0][j] = dp[0][j - 2] 且 p[j - 1] = '*'： 首行 s 为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让 p 的奇数位出现 0 次，保持 p 是空字符串）。因此，循环遍历字符串 p ，步长为 2（即只看偶数位）。
class Solution {
public:
bool isMatch(string s, string p) {
int n = s.length();
int m = p.length();
vector<vector<bool>> dp(n+1,vector<bool>(m+1,false));
dp[0][0] = true;
for(int i=2;i<m+1;i+=2) dp[0][i] = dp[0][i-2] && (p[i-1] == '*');
for(int i=1;i<n+1;i++){
for(int j=1;j<m+1;j++){
if(p[j-1] == '*'){
//因为‘*’不会出现在字符串p的第一个字符位置，所以进入该判断语句时j>=2
if(dp[i][j-2]) dp[i][j] = true;
else if(s[i-1] == p[j-2] && dp[i-1][j]) dp[i][j] = true;
else if(p[j-2] == '.' && dp[i-1][j]) dp[i][j] = true;
}
else if(dp[i-1][j-1]){
if(s[i-1] == p[j-1] || p[j-1] == '.') dp[i][j] = true;
}
}
}
return dp[n][m];
}
};字符串转整数（剑指67题）
写一个函数 StrToInt，实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。
首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。
注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。
在任何情况下，若函数不能进行有效的转换时，请返回 0。
说明：假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为
。如果数值超过这个范围，请返回 INT_MAX 或 INT_MIN。
输入: "0004193 with words" 输出: 4193 输入: "words and 987" 输出: 0
关于字符的读取，老生常谈，这里主要讨论下如何在环境只能存储32位有符号整数的情况下（即只能用int型数据）来进行字符串转整数。
数字拼接： 若从左向右遍历数字，设当前位字符为 c ，数字结果为 res ，则数字拼接公式为：
数字越界处理：
题目要求返回的数值范围应在 ，因此需要考虑数字越界问题。而由于题目指出 环境只能存储 32 位大小的有符号整数 ，因此判断数字越界时，要始终保持res在 int 类型的取值范围内。在每轮数字拼接前，判断 res 在此轮拼接后是否超过2147483647，若超过则加上符号位直接返回。设数字拼接边界 bndry = 2147483647 / 10 = 214748364 ，则以下两种情况越界：
res>bndry 情况一：执行拼接10×res≥2147483650越界
res=bndry,x>7 情况二：拼接后是2147483648或2147483649越界
class Solution {
public:
int strToInt(string str) {
int len = str.length(),i=0;
int res = 0;
bool isnegative = false;
while(i<len&&str[i] == ' ') i++;//删除空格
if(i == len) return 0;
if(str[i] == '+'||str[i] == '-'){
if(str[i] == '-') isnegative = true;
i++;
}
while(i<len&&str[i]>='0'&&str[i]<='9'){
if(res > 214748364) return isnegative?INT_MIN:INT_MAX;
if(res> 214748363 && str[i]>'7') return isnegative?INT_MIN:INT_MAX;
res = res * 10 +(str[i]-'0');
i++;
}
return isnegative?-res:res;
}
}最长回文字串——即正着读反着读都一样（第５题）
给你一个字符串 s，找到 s 中最长的回文子串。
示例 1： 示例 2：
输入：s = "babad" 输入：s = "cbbd"
输出："bab"或"aba" 输出："bb"
示例 3： 示例 4：输入：s = "a" 输入：s = "ac"
输出："a" 输出："a"
中心扩散法（较易理解，时间空间占用较小）
中心扩散法其实就是，对于从s[i]到s[j]的子字符串，判断从s[i-1]到[j+1]子字符串是否也为回文子串，由一个初始的字符串向两端不断扩散。
对于初始子字符串，应该有两种情况：即含一个字符和含有两个字符。对于一个长度为len的字符串，需要遍历两次，第一次为遍历len个的所有单个字符，第二次为遍历len-1个双字符，总共需要遍历2*len-1次。
针对中心扩散法，有两种代码书写思路：
第一种是比较常规的书写，将遍历分为两次。
class Solution {
public:
string longestPalindrome(string s) {
if (s.size() < 1)return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++){
int len1 = expandAroundCenter(s, i, i);//一个元素为中心
int len2 = expandAroundCenter(s, i, i + 1);//两个元素为中心
int len = max(len1, len2);
if (len > end - start){
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substr(start, end - start + 1);
}
int expandAroundCenter(string &s, int left, int right){
int L = left, R = right;
while(L>=0 && R<s.size() && s[L]==s[R]){//计算以left和right为中心的回文串长度
L--;
R++;
}
return R - L - 1;
}
};第二种方法比较特殊，在思想上取了巧。既然知道进行中心扩散法需要遍历2*len-1次，那么直接建立一个遍历2*len-1次的循环，将i从0遍历到2*len-2，一次性把单字符和双字符的扩散法写出来。先初始化子字符串的左右索引值left和right。现设定当单字符扩散时left==right，双字符扩散时right=left+1，
对于2*len-2，将其除以2，将得到从 0,0,1,1,2,2,3,3....len-1,len-1两组从0到len-1的数字，而这也对应了单字符和双字符两种情况下的子字符串索引值，当i为奇数时，对应双字符的情况，当i为偶数时，对应单字符的情况。代码如下：
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
int maxLen = 1，begin = 0;
for(int i=0;i<2*n-1;i++){
int left = i/2;
int right = left+i%2;
while(left>-1&&right<n&&s[left]==s[right]){
if(right-left+1>maxLen){
maxLen=right-left+1;
begin=left;
}
left--;
right++;
}
}
return s.substr(begin, maxLen);
}
};动态规划法（有点繁琐 占用时间空间较大 但思路值得学习）
定义了一个二维数组dp[i][j]；它表示从s[i]到s[j]是否为回文串，对于i与j，可以理解为字符串左边界索引值i以及右边界值j。并且若dp[i][j]=1，s[i-1]!=s[j+1]，表示此回文串两端的字符s[i-1],s[j+1]不相等，所以dp[i-1][j+1]=0。注意：此处的每个dp[i][j]值理解为字符串从s[i]到s[j]是否为回文串的标识符，并进行编程，若将其理解成二维数组而考虑数组的结构以及赋值问题的话，会将此题复杂化。
class Solution {
public:
string longestPalindrome(string s) {
string res;
int len = s.length(), begin, max = 1;
if(len < 2) return s;
vector<vector<bool>> dp(len, vector<bool>(len, 0));
for(int i = len -1; i > -1; i--){
for(int j = i; j < len; j++){
if(s[i] == s[j]){
if(j - i < 3) dp[i][j] = 1;
else dp[i][j] = dp[i+1][j-1];//需要提前知道i+1与j-1,所以i的遍历要从后往前
}
if(dp[i][j] && j - i + 1 > max){
max = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, max);
}
};整数转罗马数字（第12题）——简单的枚举分类题
罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给你一个整数，将其转为罗马数字
我的解法
class Solution {
public:
string s;
string intToRoman(int num) {
int a=num%10,b=(num/10)%10,c=(num/100)%10,d=num/1000;
if(d!=0) s.insert(0,d,'M');
if(c!=0) help(c,"CD","CM",'D','C');
if(b!=0) help(b,"XL","XC",'L','X');
if(a!=0) help(a,"IV","IX",'V','I');
return s;
}
void help(int temp,string s1,string s2,char c1,char c2){
if(temp==4) s.append(s1);
else if(temp==9) s.append(s2);
else if(temp==5) s.push_back(c1);
else if(temp<4) s.append(temp,c2);
else{
s.push_back(c1);
s.append((temp-5),c2);
}
}
};巧妙解法
class Solution {
public:
string intToRoman(int num) {
int values[]={1000,900,500,400,100,90,50,40,10,9,5,4,1};
string reps[]={"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
string res;
for(int i=0; i<13; i++){
while(num>=values[i]){
num -= values[i];
res += reps[i];
}
}
return res;
}
};最长有效括号
给你一个只包含
'('和')'的字符串，找出最长有效（格式正确且连续）括号子串的长度。输入：s = ")()())" 输出：4 解释：最长有效括号子串是 "()()"输入：s = ")(()())" 输出：6 解释：最长有效括号子串是 "(()())"
对于括号类的题目，一般都用栈结构来解决，与上一题不同的是，此题要求的是有效括号的长度，并且要求其最大值。如果栈中像之前一样存储左括号'('，在出栈时没有办法确定有效括号的长度值，所以此题的关键在于入栈时存储左括号在字符串中的下标，这样在出栈时就能确定有效长度了。
针对栈，有两种解法
一种是用栈遍历字符串，把字符串分割成一段一段的有效括号组，然后再求其中长度的最大值。
具体做法是额外创建一个vector数组，长度与字符串相同，事先置0，与字符串中的元素一一对应。接着将字符串中左括号的下标值入栈，当遇到右括号时，将栈顶元素弹出。如果此时栈中没有元素，则将vector数组中右括号对应的下标值置为一，表示此括号无法构成有效括号组。当遍历完字符串后将栈中剩下的元素在vector中对应的值置一，表示这些左括号也不能构成有效括号组，最后计算vector数组中元素0的最长连续长度。
考虑到10010000这样的最长连续子数组造vector尾部的情况，在vector尾部再插入一个1。以元素1为停止位遍历vector。
class Solution {
public:
int longestValidParentheses(string s) {
int len = s.length();
if(len<2) return 0;
stack<int> memory;
vector<bool> vec(len,0);
int res = 0 ,temp = 0;
for(int i=0;i<len;i++){
if(s[i]=='(') memory.push(i);
else{
if(!memory.empty()) memory.pop();
else vec[i] = 1;
}
}
while(!memory.empty()){
vec[memory.top()] = 1;
memory.pop();
}
vec.push_back(1);
for(int i=0;i<len+1;i++){
if(!vec[i]) temp++;
else {
res = max(temp,res);
temp = 0;
}
}
return res;
}
};另一种做法比较难想到
具体做法是我们始终保持栈底元素为当前已经遍历过的元素中[最后一个没有被匹配的右括号的下标]，这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：
对于遇到的每个 ‘(’ ，我们将它的下标放入栈中
对于遇到的每个 ‘)’ ，我们先弹出栈顶元素表示匹配了当前右括号：
- 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。
需要注意的是，如果一开始栈为空，第一个字符为左括号的时候我们会将其放入栈中，这样就不满足提及的「最后一个没有被匹配的右括号的下标」，为了保持统一，我们在一开始的时候往栈中放入一个值为 -1 的元素。
class Solution {
public:
int longestValidParentheses(string s) {
int maxans = 0;
stack<int> stk;
stk.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') stk.push(i);
else {
stk.pop();
if (stk.empty()) stk.push(i);
else maxans = max(maxans, i - stk.top());
}
}
return maxans;
}
};删除无效的括号（力扣第301题）
给你一个由若干括号和字母组成的字符串
s，删除最小数量的无效括号，使得输入的字符串有效。返回所有可能的结果。答案可以按 任意顺序 返回。输入：s = "()())()" 输出：["(())()","()()()"]
很难的题，深度优先遍历法，具体思想就是遍历字符串s，构建其中所有子字符串（全排列）。当碰见子字符串的中左右括号数量相平衡并且此字符串的长度是最长的有效子字符串，就将该子字符串记录下来。
我们知道所有的合法方案，必然有左括号的数量与右括号数量相等。
首先我们令左括号的得分为 1；右括号的得分为 -1。则会有如下性质：对于一个合法的方案而言，必然有最终得分为 0；搜索过程中不会出现得分值为 负数 的情况（当且仅当子串中某个前缀中「右括号的数量」大于「左括号的数量」时，会出现负数，此时不是合法方案）。
直接看代码
class Solution {
private:
int maxscore;
int length;
int n;
unordered_set<string> hash;
public:
void dfs(string & s, int score, string buf, int l, int r, int index){//不断向字符串buf中填入字符
//score指的是字符串buff中，左括号与右括号的分数之和
if (l < 0 || r < 0 || score < 0 || score > maxscore) return;
//如果出现删过头（即l或r<0）的情况，或分数出现负数或超过最大值，返回
if (score == 0 && buf.length() == length) hash.insert(buf);
//当前字符串的左右括号相匹配，并且长度也符合最长长度
if (index == n ) return;
char ch = s[index];
if (ch == '('){
dfs(s, score + 1, buf + '(', l, r, index + 1);
//添加一个左括号到buff中，则+1分，继续遍历
dfs(s, score, buf, l - 1, r, index + 1);
/*不添加左括号到buff中，相当于把s字符串中当前位置的左括号删除，
则多余的左括号数要减一，分数score不变*/
}
else if(ch == ')'){
dfs(s, score - 1, buf + ')', l, r, index + 1);//选择添加右括号，则-1分
dfs(s, score, buf, l, r - 1, index + 1);
//同上 选择不添加右括号，多余的右括号数要减一，分数score不变
}
else{
dfs(s, score, buf + ch, l, r, index + 1);//遇到其他字符，直接添加，继续遍历
}
}
vector<string> removeInvalidParentheses(string s) {
//假设 "(" 为+1分, ")" 为-1分，那么合规的字符串分数一定是0
/*分数一定不会是负数，因为那样意味着到当前位置')'比'('多，
无论后面怎么加括号，都不可能合规*/
//分数一定不会超过maxscore，maxscore就是所有可匹配的左右括号的个数
maxscore = 0;
n = s.size();
int left = 0, right = 0;//统计字符串是中，左右括号数量
int l = 0, r = 0;//字符串s中，需要删除的左右括号数量
for (auto& ch:s){
if (ch == '(') {
l++;
left++;
}
else if (ch == ')'){
if (l != 0) l--; //遇到可匹配的右括号
else r++;
right++;
}
}
length = n - l - r;//排除需要删除的左括号和右括号后，最后输出的字符串应该有的长度
maxscore = min(left, right);
//最大分数为左括号右括号数量中的较小值
dfs(s, 0, "", l, r, 0);
return {hash.begin(), hash.end()};
}
};最小覆盖子串（力扣76） 较难理解
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。
注意：
对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。输入：s = "ADOBECODEBANC", t = "ABC"输出："BANC"
辣鸡csdn 写一半网页关了，不想再写了，直接看代码 解析
class Solution {
public:
string minWindow(string s, string t) {
int len1 = s.size(), len2 = t.size();
if (len1 < len2) return "";
int left = 0, right = 0, count = len2;
unordered_map<char, int> memory;
string res = "";
for (auto word : t) memory[word]--;
while (right < len1) {
while (right < len1 && count > 0) {
if (memory[s[right]] > 0) count--;
memory[s[right++]]++;
}
if(count != 0) break;
while (memory[s[left]] < 0) memory[s[left++]]++;
if(right - left < res.size() || res == ""){
res = s.substr(left, right - left );
}
count++;
memory[s[left++]]++;
}
return res;
}
};😈😈第139题：单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明：拆分时可以重复使用字典中的单词；可以假设字典中没有重复的单词。
输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。 注意：可以重复使用字典中的单词。
这一题是典型的背包问题，其中背包是字符串字典worddict，要从背包中取出元素，来组成字符串，并且背包中的元素没有个数限制。
一般背包问题用动态规划法来解决，并且要用两层for循环。用动态数组dp[i]表示字符串s的前i个字符能否拆分。动态数组的长度为字符串s的长度加一，waicengfor循环遍历字符串s中的元素，内层for循环则遍历字符串字典，判断i-word.size()对应的子字符串能否被字符串字典所表示。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int len = s.length();
vector<bool> dp(len+1, 0);
dp[0] = 1;
for(int i = 1; i < len + 1; i++){
for(auto word : wordDict){
int size = word.size();
if(i < size) continue;
if( !dp[i - size]) continue;
else if(s.substr(i - size, size) == word) {
dp[i] = 1;
break;
}
}
}
return dp[len];
}
};KMP算法——实现strstr(力扣第28题)
KMP算法有两个关键的部分：求取next数组和利用next数组遍历待查找字符串。该方法只需要遍历一次字符串就能找到子字符串。原因是它将之前的查找信息记录了下来并作为后面查找时的参考。当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。
先介绍next数组以及其求取方法
next数组又叫前缀表，对于next[i]，它表示待查找字符串从下标0到下标i的字符串中，最大相同前后缀的长度。
- 前缀子串表示所有以第一个字符开头的不包含最后一个字符的连续子串。
- 后缀子串表示所有以最后一个字符结尾的不包含第一个字符的连续子串。
最大相同前后缀则是指对于一个字符串，它拥有的长度内容都相同的前缀子串和后缀子串的长度。
一个字符串的next数组，例如字符串 aaabbab，它的next数组是 0120010，
对于next[0]，它的值一定为0，因为next[0]下，字符串只有一个字符，而前缀和后缀子串都要求去掉首部或尾部字符，所以这种情况下，前缀和后缀子串的值都为0。
求取一个字符串str的next数组，即从1一直遍历到str.length()-1依次求取的过程。
注意，上述next[i]表示str.substr(0,i+1)字符子串中，最大相同前后缀的长度，也可以理解为该子串最大相同前后缀中前缀子串尾部元素的下标值加一的结果。为了后面表示方便，更新一下next数组的含义：next[i] 表示以s[i]结尾的子字符串的最大前后缀长度 - 1 也可以理解为是最大前后缀中前缀字符串的尾部字符在总字符串中的索引值。
在顺序求取next数组的过程中，用i来表示当前求取next元素的索引值，strlen表示上一个最大相同前后缀的长度，无非就两种情况：
当遍历到i，准备求取next[i]时，已知next[i - 1] = strlen；最大相同前后缀的长度为strlen+1
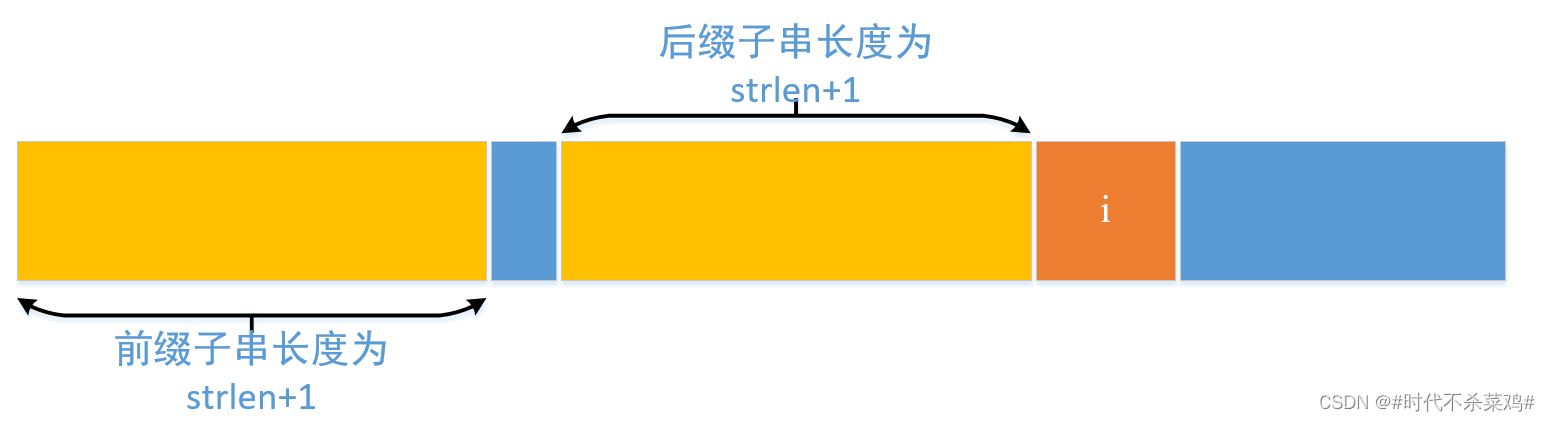
- 如果s[strLen + 1] == s[i]，那么最大相同前后缀的长度在原来的基础上直接加一即可，同时i也后移一位。
- 如果s[strLen + 1] != s[i]，那么当前以str[i]结尾的子串的最大相同前后缀的长度肯定小于strlen，需要在以str[strlen]结尾的子串里查找，是否有其他的前缀子串，使得存在后缀子串与其匹配。
如图，绿色括号区域如果存在的话，那么这三部分就一定相等，那么next[i] = next[strlen] + 1；
重点就是判断，这三个区域是否存在，也就是判断next[strlen]的取值，
如果next[strlen]大于等于0，那么就代表，以str[strlen]结尾的子串存在相同前后缀子串，将strlen的更新，再次进行s[strLen + 1] 与 s[i]的判断。
如果next[strlen]的值小于0(即为-1)，就代表最左边括号的区域不存在，那么就无法进行s[strLen + 1] 与 s[i]的判断，但是此时还要考虑一下s[0]与s[i]的相等关系（容易被忽略），如果它们两个也不相等，那就确定next[i]的值为-1了。
至此，next数组已经求取完毕，接下来就是借助next数组来在字符串中寻找子字符串。
编辑
如果两个下标值对应的字符不相等，那么就要进行讨论。如上图所示，当原串到字符a，子串到字符f时，两者不相等，也就是说原串以下标值0开头的的子字符串中没有与匹配串相等的，按理说就要从下标为1的字符开始从头判断。但是有了next数组，原串的下标值不需要作回退操作，只需要匹配串的下标值移动到其next数组对应的值上后再继续判断。
而如果匹配串对应的字符的下标在next数组中的值为-1，那么就只能从头开始判断了
class Solution {
public:
int strStr(string haystack, string needle) {
int len = needle.length();
if(len == 0) return 0;
vector<int> next(len, -1);
getNext(needle, next);
int index = 0;
for(int i = 0; i < haystack.length(); i++){
if(haystack[i] == needle[index]) index++;
else{
while(index > 0 && haystack[i] != needle[index])
index = next[index - 1] + 1;
//结束while循环之后 index的值要么是0（表示没有最大前后缀）
//或者是最大前缀字符串的后一个字符的索引值
if(haystack[i] == needle[index]) index++;
}
if(index == len) return i - index + 1;
}
return -1;
}
void getNext(string & s, vector<int> & next){
//next[i] 表示以s[i]结尾的字符串的最大前后缀长度 - 1
//或者是最大前后缀中前缀字符串的尾部字符的索引值
int i = 1, len = s.length();
int strLen = -1;//strLen为-1的意义 对应着字符串s[0]
while(i < len){
if(s[strLen + 1] == s[i]){
strLen++;
next[i++] = strLen;
}
else{
strLen = (strLen == -1 ? -1 : next[strLen]);
if(strLen == -1 && s[0] != s[i]){
next[i] == -1;
i++;
}
}
}
return;
}
};贴上简化后的代码
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) j = next[j];
if (s[i] == s[j + 1]) j++;
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) return 0;
int next[needle.size()];
getNext(next, needle);
int j = -1;
for (int i = 0; i < haystack.size(); i++) {
while(j >= 0 && haystack[i] != needle[j + 1]) j = next[j];
if (haystack[i] == needle[j + 1]) j++;
if (j == (needle.size() - 1) ) return (i - needle.size() + 1);
}
return -1;
}
};
歪门邪道🤡
剪绳子问题/整数拆分问题😭（剑指14题，力扣343题）
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
此题涉及到一个定理：对于一个整数n，关于其拆分得到的值之积：当n>3时，当拆得多个整数相等并且这几个整数都为3时，所得到的积最大。例如对于数字6，拆分所得到的数的最大乘积为3x3=9，其他的拆分方式都没有9大。当拆分完尽可能多的数字3之后，余下的数由三种情况0,1,2。下面进行分类讨论：
假设n=3xa+b;
b=0 max=
。
b=1 max有两种情况: max=
， 选择后者。
b=2 max有两种情况: max=
， 选择前者。
代码如下：
class Solution {
public:
int cuttingRope(int n) {
if(n<3) return 1;
if(n==3) return 2;
int a=n/3,b=n%3;
switch(b){
case 0:return pow(3,a);break;
case 1:return pow(3,a-1)*4;break;
case 2:return pow(3,a)*2;break;
}
return 0;
}
};此题中对结果还有取余操作，当计算得到的结果超出int型数据的上界时，上述代码就会出错，所以需要解决大数取余的问题。首先要明确这样的一个公式：
上式是一个对乘积取余的公式，对于来说，对其进行取余操作，p=1000000007，可写成：
用下标p表示对p取余，上面公式可变成:
此时得到了对幂次方数的取余方法，接下来要考虑的就是，如何将上面三种情况下得到的结果进行取余。三种情况的结果分别是： ,此处统一考虑成对
进行取余，得到的结果再根据不同的情况进行运算。
代码如下：
class Solution {
public:
int cuttingRope(int n) {
if(n<3) return 1;
if(n==3) return 2;
int a=n/3,b=n%3,p=1000000007;
long long res=1;
//因为res要存储p*6的结果，对于int数据来说会产生越界，要改用long long
for(int i=1;i<a;i++) res=(res*3)%p; //对3的a-1次方进行取余运算
switch(b){
case 0:return res*3%p; break;
case 1:return res*4%p; break;
case 2:return res*6%p; break;
}
return 0;
}
};比特位计数（第338题）进一步理解二进制的进位
给你一个整数
n，对于0 <= i <= n中的每个i，计算其二进制表示中1的个数 ，返回一个长度为n + 1的数组ans作为答案。输入：n = 2 输出：[0,1,1] 解释：0 --> 0 1 --> 1 2 --> 10
对于将二进制来说，若前一个数是后一个数的两倍，那么相当于将前一个数总体左移一位，那么实际两个数的比特1的位数没有改变，如3—011与6—110，进一步可得：
- 如果一个数i为偶树，那么这个数中比特1的个数与其一半的数i/2相同，
- 而如果一个数i为奇数，那么这个数中比特1的个数比i-1多一个，因为i-1是偶数，而偶数的二进制的最低位是0，比它大一的奇数的二进制之表示就是在最低位直接加1
可得代码：
class Solution {
public :
vector<int> countBits(int num) {
vector<int> dp(num+1);
dp[0]=0;
for(int i=0;i<=num;i++){
if(i%2==0) dp[i]=dp[i/2];
else dp[i]=dp[i-1]+1;
}
return dp;
}
};约瑟夫环问题——（剑指62题）
0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。
例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。
如下
关于上面的题解，做一点补充说明：
表示对0到n-1这n个有序数列删除一次后，对剩下的数列进行删除直到只剩一个数字，
则表示，对0到n-1这n个有序数列进行连续两次删除后，对剩下的数列进行删除直到只剩一个数字，上述两种情况因为从数列中删除了数字，所以数列不是严格加1递增的。
而
则表示对从0到n-2严格加一递增的数列不断删除数字直到只剩一个数字的情况。
class Solution {
public:
int lastRemaining(int n, int m) {
int x = 0;
for (int i = 2; i <= n; i++) {
x = (x + m) % i;
}
return x;
}
};
幂次方运算（第50题）
实现 pow(x, n) ，即计算 x 的 n 次幂函数（即 ）。
分析：
则只需要作 次运算即可，每次计算x的平方值。
class Solution {
public:
double myPow(double x, int b) {
if(x==0) return 0;
double res=1.0;
for(int i=b;i!=0;i=i/2){
if(i&1) res*=x;
x=x*x;
}
return b>0?res:1/res;
}
};求1+2+3+...n(剑指 64题)
求
1+2+...+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。
法一
逻辑运算符的短路效应：
常见的逻辑运算符有三种，即 “与 \&\&&& ”，“或 ||∣∣ ”，“非 !! ” ；而其有重要的短路效应，如下所示：
if(A && B) // 若 A 为 false ，则 B 的判断不会执行（即短路），直接判定 A && B 为 false
if(A || B) // 若 A 为 true ，则 B 的判断不会执行（即短路），直接判定 A || B 为 true本题需要实现 “当 n = 1n=1 时终止递归” 的需求，可通过短路效应实现。
n > 1 && sumNums(n - 1) // 当 n = 1 时 n > 1 不成立 ，此时 “短路” ，终止后续递归代码如下：
class Solution {
public:
int sumNums(int n) {
int res=n;
n>0&&(res+=sumNums(n-1)); // 递归实现
return res;
}
};法二 天秀
sizeof（）以字节为单位计算存储空间大小，bool占一个字节空间，bool类型的二维数组a[n][n+1]的大小为n*(n+1)，而1+2+3+...+n=n*(n+1)/2
class Solution {
public:
int sumNums(int n) {
bool a[n][n+1];
return sizeof(a)>>1;
}
};
//ans=1+2+3+...+n
// =(1+n)*n/2
// =sizeof(bool a[n][n+1])/2
// =sizeof(a)>>1不用加减乘除做加法（剑指65题）
写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
输入: a = 1, b = 1 输出: 2
a,b均可能是负数或 0 结果不会溢出 32 位整数
计算机在存储数据时都是以补码形式进行存储，当进行加减乘除运算以及位运算时也是，统一对数据的补码进行运算，最后运算的结果再转化成原码输出在终端上。
计算机在计算两个数的加法时，不论两个数的正负，同一将两数的补码进行加操作，最后得到的结果在进行一次补码转换操作，即可得到最终的结果。
所以本题主要研究如何对两个二进制数进行加操作。
先用1位数的加法来进行，在不考虑进位的基础上，如下
1 + 1 = 0
1 + 0 = 1
0 + 1 = 1
0 + 0 = 0很明显这几个表达式可以用位运算的“^”来代替，如下
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0这样就完成了简单的一位数加法，那么要进行二位的加法 要获取进位 可以如下思考：
0 + 0 = 0
1 + 0 = 0
0 + 1 = 0
1 + 1 = 1换个角度看就是这样
0 & 0 = 不进位
1 & 0 = 不进位
0 & 1 = 不进位
1 & 1 = 进位正好，在位运算中，我们用“<<”表示向左移动一位，也就是“进位”。那么我们就可以得到如下的表达式到这里，我们基本上拥有了这样两个表达式
- x^y //执行加法
- (x&y)<<1 //进位操作
当然，加法操作的结果加上进位的结果仍有可能 产生进位，则循环上述过程，知道进位结果为0。
此外，c++中，不支持负数的左位移，因为产生的结果可能不确定，所以int型的数据（x&y）在执行左移时会报错，将其转换成unsigned int 这样虽然二进制码不变，但是可以进行左移操作。
class Solution {
public:
int add(int a, int b) {
int temp;
while(b){
temp=a^b;
b=(unsigned)(a&b)<<1;
a=temp;
}
return a;
}
};下一个排列（力扣31题）
给你一个数组，给出在该数组的元素的所有可能排列组合中，下一个大于当前数组所表示的
值的排列组合，比如给你一个数组[1,2,5,3] 它的下一个排列组合是[1,3,2,5] ，类似的的还有
[1,3,5]->[1,5,3], [3,5,2,4]->[3,5,4,2]
如果当前数组后面没有比它所表示的值更大的排列组合，那么就返回值最小的排列。比如
[3,2,1]->[1,2,3]
此题的意思就是在数组所能排列成的所有组合里，找出下一个比当前数组所表示十进制数字大的组合。
如何得到这样的排列顺序？这是本文的重点。我们可以这样来分析：
我们希望下一个数比当前数大，这样才满足“下一个排列”的定义。因此只需要将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
我们还希望下一个数增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求，我们需要：
在尽可能靠右的低位进行交换，需要从后向前查找
将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
将「大数」换到前面后，需要将「大数」后面的所有数重置为升序，升序排列就是最小的排列。以 123465 为例：首先按照上一步，交换 5 和 4，得到 123564；然后需要将 5 之后的数重置为升序，得到 123546。显然 123546 比 123564 更小，123546 就是 123465 的下一个排列
以上就是求“下一个排列”的分析过程。
算法过程
标准的“下一个排列”算法可以描述为：
- 从后向前查找第一个相邻升序的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
- 在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
- 将 A[i] 与 A[k] 交换
- 可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
- 如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int len = nums.size();
int i = len - 1;
while (i > 0 && nums[i-1] >= nums[i]) i--;
if (i == 0) {
reverse(nums.begin(), nums.end());
return;
}
int j;
for(j = len - 1; j >= i; j--){
if(nums[j] > nums[i-1]) break;
}
swap(nums[j],nums[i-1]);
reverse(nums.begin() + i, nums.end());
}
};数组排序
数组的排序：一种高效的方法 三路快排（第75题）
给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。此题中，使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
示例：输入：nums = [2,0,2,1,1,0] 输出：[0,0,1,1,2,2]
分析：此题是对三个元素的0，1，2的重新排序，并且题目要求原地排序，那么只有用swap()函数了，关于swap()函数，有一个比较重要的用法:
int start=0;
int i=0;
while(i<len){
if(nums[i]==0)
swap(nums[start++],nums[i]);
i++;
}以上代码的作用是通过遍历，将所有为0的元素都放到数组的最前面，因为元素的排序是通过swap()函数实现的，所以数组内总的元素还是没有改变。
以下是完整代码：将0放到数组最前端，将2放到数组最后端。
class Solution {
public:
void sortColors(vector<int>& nums) {
int i=0;
int start=0;
int len=nums.size();
int end=len-1;
while(i<=end){
if(nums[i]==0)
swap(nums[start++],nums[i++]);
else if(nums[i]==1)
i++;
else
swap(nums[end--],nums[i]);
}
}
};注意：此处的循环使用的是while循环，而不是for循环，因为for循环中的变量i在循环体中也要用到，而for循环中的i++会影响到循环体中i的取值。
此题是三路快速排序的简化版 快速排序 详解（快速排序 双路快排 三路快排）_k_koris的博客-CSDN博客_三路快排
三路快排是快速排序算法的升级版，用来处理有大量重复数据的数组。主要思想是选取一个key，小于key的丢到左边，大于key的丢到右边，递归实现即可。
#include<iostream>
using namespace std;
void swap(int &a, int &b){
int t = a;
a = b;
b = t;
}
void triSort(int *a, int low, int high){
if(low >= high)return;
int key = a[low];
int i = low, j = low;
int k = high;
while( i <= k){
if(a[i] < key) swap(a[i++], a[j++]);
else if(a[i] > key) swap(a[i], a[k--]);
else i++;
}
triSort(a, low, j);
triSort(a, k + 1, high);
}
int main(){
int n[12] = {5, 9, 0, 1, 6, 3, 8, 7, 2, 4, 4, 4};
triSort(n, 0, 11);
for(int i = 0; i < 12; i++){
cout<<n[i]<<" ";
}
cout<<endl;
return 0;
}最小的k个数——数组的快速排序（剑指第40题）
输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。
输入：arr = [3,2,1], k = 2 输出：[1,2] 或者 [2,1]
这道题是一个经典的 Top K 问题，是面试中的常客。Top K 问题有两种不同的解法，一种解法使用堆（优先队列），另一种解法使用类似快速排序的分治法。
堆（优先队列）
比较直观的想法是使用堆数据结构来辅助得到最小的 k 个数。堆的性质是每次可以找出最大或最小的元素。我们可以使用一个容量为 k 的最大堆（大顶堆），将数组中的元素依次入堆，当堆的大小超过 k 时，便将多出的元素从堆顶弹出。以数组 [5, 4, 1, 3, 6, 2, 9]， k=3 为例展示元素入堆的过程：
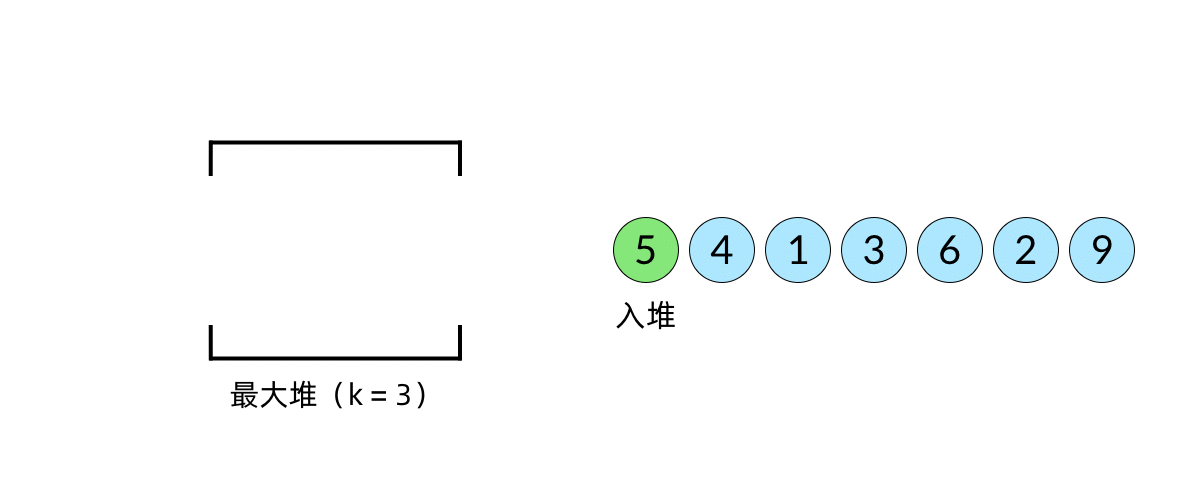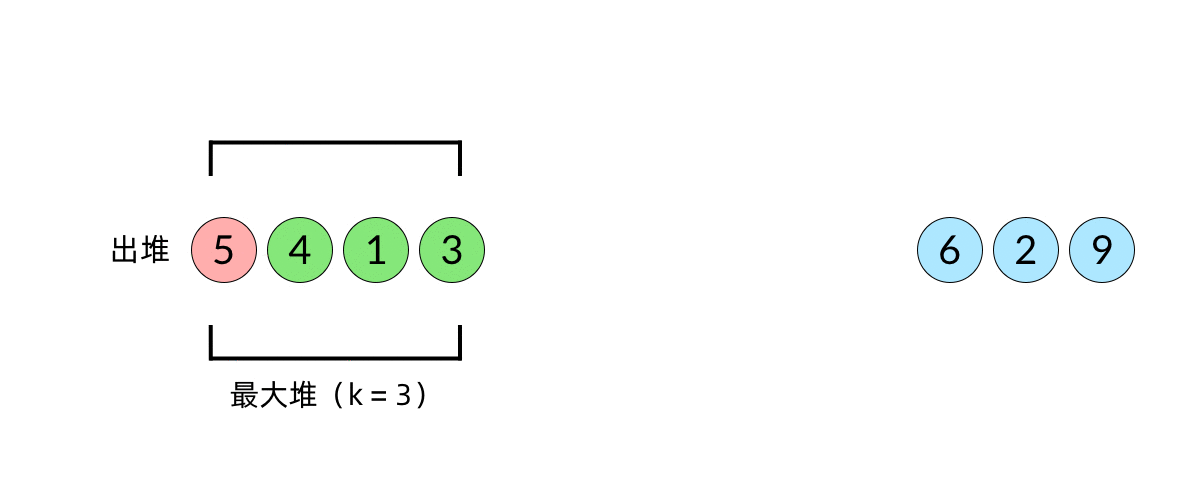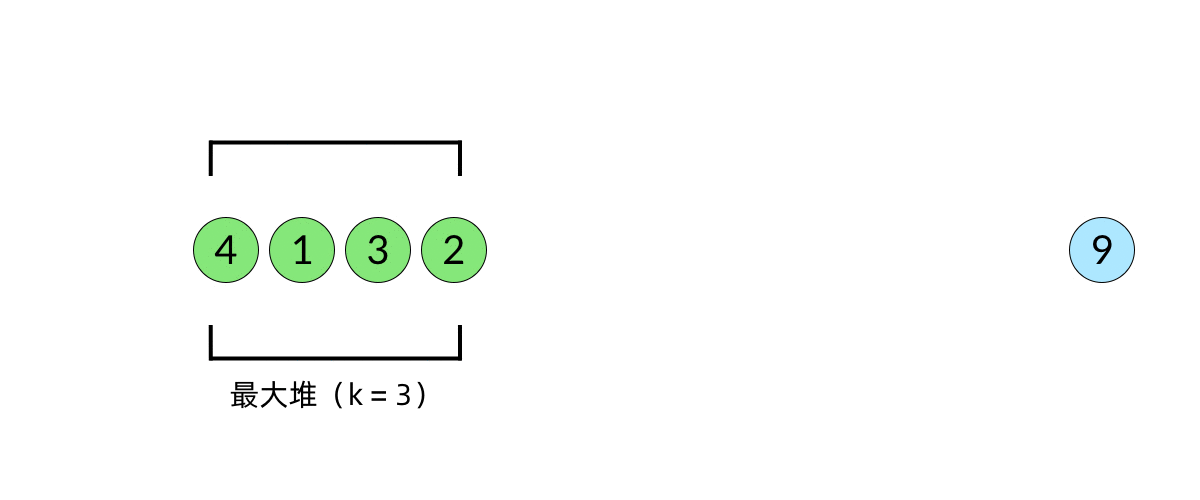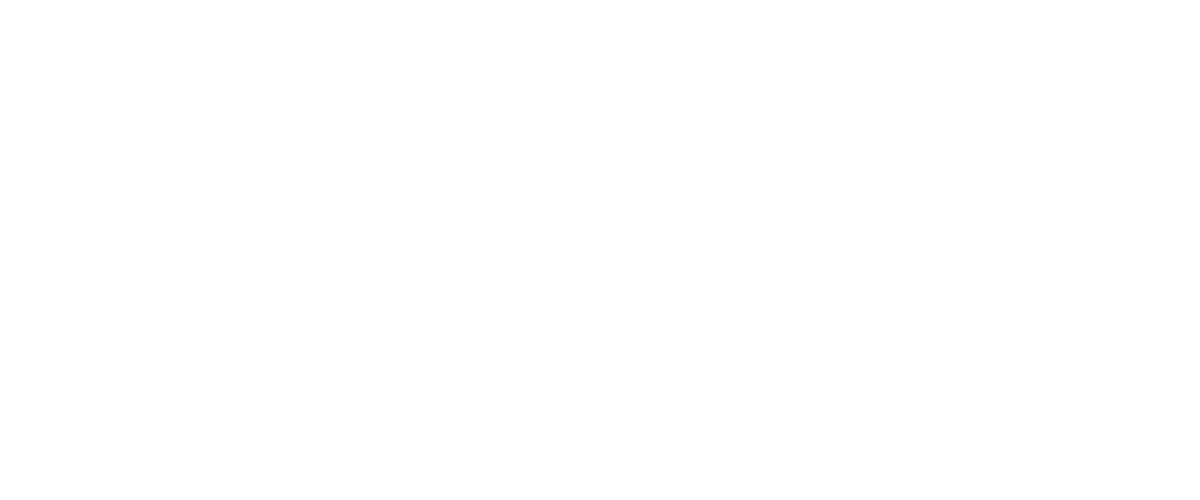
这里使用STL中已有的数据结构 优先队列——priority queue。代码如下
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res;
if(k==0) return res;
priority_queue<int> memory;
for(int i=0;i<k;i++) memory.push(arr[i]);
for(int i=k;i<arr.size();i++){
if(arr[i]<memory.top()){
memory.pop();
memory.push(arr[i]);
}
}
for(int i=0;i<k;i++){
res.push_back(memory.top());
memory.pop();
}
return res;
}
};快速排序
此方法的基础是快速排序方法，快速排序法的关键就是找到一个哨兵元素，然后将数组中大于哨兵元素的值统一放到右边，将小于哨兵元素的值统一放到数组的左边，最后将哨兵元素放到这两块区域的中间 ，接着对两边的区域内的元素进行同样的操作，直到区域的长度变为一 。
过程如下：
- 选出一个key，一般是最左边或是最右边的。
- 定义一个begin和一个end，begin从左向右走，end从右向左走。（需要注意的是：若选择最左边的数据作为key，则需要end先走；若选择最右边的数据作为key，则需要bengin先走）。
- 在走的过程中，若end遇到小于key的数，则停下，begin开始走，直到begin遇到一个大于key的数时，将begin和right的内容交换，end再次开始走，如此进行下去，直到begin和end最终相遇，此时将相遇点的内容与key交换即可。（选取最左边的值作为key）
- 此时key的左边都是小于key的数，key的右边都是大于key的数
- 将key的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作，此时此部分已有序
当做完上述的操作之后，该数组就会变的有序 ，最后取前面k个元素即可。贴上快速排序的经典代码：
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
quickSort(arr, 0, arr.size() - 1);
vector<int> res;
res.assign(arr.begin(), arr.begin() + k);
return res;
}
private:
void quickSort(vector<int>& arr, int l, int r) {
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作（以 arr[l] 作为基准数）
int i = l, j = r;
while (i < j) {
while (i < j && arr[j] >= arr[l]) j--;
while (i < j && arr[i] <= arr[l]) i++;
swap(arr[i], arr[j]);
}//循环结束时i=j
swap(arr[i], arr[l]);
// 递归左（右）子数组执行哨兵划分
quickSort(arr, l, i - 1);
quickSort(arr, i + 1, r);
}
};优化：此题中只要求找出数组中前k个最小的，那么在进行快速排序时，哨兵元素在数组中的索引值i为k时即可退出。
- 若 k < i ，代表当前在左子数组中找到的，前i个最小的元素的个数大于k，需要在左子数组中进一步排序；
- 若 k > i ，代表当前在左子数组中找到的，前i个最小的元素的个数小于k，需要在右子数组中进一步排序；
- 若 k = i，当前哨兵是第k+1个最小的元素，直接返回前k个数字即可；
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
if(k>=arr.size()) return arr;
return fun(arr,k,0,arr.size()-1);
}
vector<int> fun(vector<int> & arr,int k,int left,int right){
int i=left,j=right;
while (i < j) {
while (i < j && arr[j] >= arr[left]) j--;
while (i < j && arr[i] <= arr[left]) i++;
swap(arr[i], arr[j]);
}
swap(arr[i], arr[left]);
if(i>k) return fun(arr,k,left,i-1);
if(i<k) return fun(arr,k,i+1,right);
arr.assign(arr.begin(),arr.begin()+i);
return arr;
}
};😈把数组排成最小的数——快排法（剑指第45题）
输入一个非负整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。
输入: [3,30,34,5,9] 输出: "3033459"
说明:
- 输出结果可能非常大，所以你需要返回一个字符串而不是整数
- 拼接起来的数字可能会有前导 0，最后结果不需要去掉前导 0
基本的想法就是将数组中的int型数据转化成string型数据，然后将string数据进行排序，最后将排序的结果进行整合。书写代码过程中，有两个难点：确定排序规则以及运用合适的排序方法。
此题中，对于多个string数据，如何确定合适的规则让这几个string数据合并后的数据最小呢？可以先考虑两个string数据情况，如何确定两个string数据的前后顺序呢？无非是分别比较两个string数据在前和在后的情况，如下：
若拼接字符串 x + y > y + x ，则 x “大于” y ；
反之，若 x + y < y + x ，则 x “小于” y ；。此处的大于小于是对于字符串的比较，若x“大于”y，则排序时string数据y应在在前，这样两string数据整合后的数字才最小。
至于排序方式，应为上面采用了两两比较的方式，所以采用快速排序。
class Solution {
public:
string minNumber(vector<int>& nums) {
vector<string> memory;
string res;
for(int num:nums) memory.push_back(to_string(num));
sort(memory,0,nums.size()-1);
for(string str:memory) res+=str;
return res;
}
void sort(vector<string> & memory,int left,int right){
if(left>=right) return;//只剩一个元素时，就停止运行函数
int i=left,j=right;
while(i<j){
while(i<j&&memory[j]+memory[left]>=memory[left]+memory[j]) j--;
while(i<j&&memory[left]+memory[i]>=memory[i]+memory[left]) i++;
swap(memory[i],memory[j]);
}
swap(memory[left],memory[i]);
sort(memory,left,i-1);
sort(memory,i+1,right);
}
};
数组中的逆序——归并排序（剑指51题）
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
输入: [7,5,6,4] 输出: 5
归并排序是逆序对问题的标准解法，关于归并排序，可总结如下：
分： 不断将数组从中点位置划分开，将整个数组的排序问题转化为子数组的排序问题；
治： 划分到子数组长度为 1 时，开始向上合并，不断将较短排序数组合并为较长排序数组，直至合并至原数组时完成排序，如下
本题关键的是如何在归并排序的过程中统计数组逆序对的数量，可作如下解释：
合并阶段本质上是合并两个有序数组为新的有序数组的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素时，意味着 「左子数组当前元素至末尾元素」 与 「右子数组当前元素」构成了若干「逆序对」 。即在归并排序向上合并数组时，统计对于右子数组的每一个元素，左子数组大于它的元素的个数。
 |  |
 |  |
class Solution {
public:
int res;
int reversePairs(vector<int>& nums) {
int length = nums.size();
if(length<2) return 0;
res=0;
vector<int> tempVec(length,0);
merge(nums,tempVec,0,length-1);
return res;
}
void merge(vector<int> &nums,vector<int> & tempVec,int left,int right){
if(left == right) return;
int mid = (left+right)>>1;
merge(nums,tempVec,left,mid);
merge(nums,tempVec,mid+1,right);//假设在nums中，下标从left到mid以及mid+1到right
//的这两组数据已经排好序，接下来要做的是将这两组数据按大小顺序合并到一块
int low1 = left,low2 = mid+1,index = left;
while(low1 <= mid && low2 <= right){
if(nums[low1] > nums[low2]){
tempVec[index++] = nums[low2++];
res += mid-low1+1;
}
else tempVec[index++] = nums[low1++];
}
while(low1 <= mid) tempVec[index++]=nums[low1++];
while(low2 <= right) tempVec[index++]=nums[low2++];
for(int i=left;i<=right;i++) nums[i] = tempVec[i];
//排好序之后将nums中下标从left到right的数据的顺序更新
}
};数组的数据处理
求出一个数组中最大的三个数和最小的两个数（第628题）
从小到大依次为 min1 min2 max3 max2 max1
int max1=INT_MIN,max2=INT_MIN,max3=INT_MIN;
int min1=INT_MAX,min2=INT_MAX;
for(auto num:nums){
if(num>max1){
max3=max2;
max2=max1;
max1=num;
}
else if(num>max2){
max3=max2;
max2=num;
}
else if(num>max3)
max3=num;
if(num<min1){
min2=min1;
min1=num;
}
else if(num<min2)
min2=num;
}😈数组中数字出现的次数（剑指第56题）
一个整型数组
nums里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。输入：nums = [1,4,6,5,1,4,6,7] 输出：[5,7] 或 [7,5`]
题目对时间复杂度和空间复杂度都有要求，不能采用常规的暴力解法或哈希表统计法，像这种要求空间复杂度为O(1)，只能采用位运算的方式，这里用到了异或运算。关于异或运算，有以下几个性质：
- 相异为1，相同为0；
- 异或运算满足乘法交换律和乘法结合律
- 两个相同的数进行异或运算，得到的是0；
- 0与任何数进行异或运算，得到的都是原来的数其本身。
此题的数组中，除了两个单独的数之外 ，其他都是一对一对的相同的数。如上例中的[1,4,6,5,1,4,6,7]，将数组中得到数据全部进行异或运算，最后得到的结果应该是5xor7，其他的数据在计算过程中全部都转化了0；
接着要做的就是根据异或运算的结果在数组中找出这两个单独的数字。不同的数据的二进制位至少有一位是不一样的，这两个单独数字的异或二进制结果中至少会有一位是1；
找到此位，则根据该二进制位是否为1可以将数组分为两组，每一组都包含一个单独的数字，剩下的都是一对一对的，接着对剩下的两组再进行一次异或运算。太精妙了
代码如下：
class Solution {
public:
vector<int> singleNumbers(vector<int>& nums) {
int x=0,y=0,z=1,i=0;
for(auto num:nums) i^=num;
while(!(i&z)) z=z<<1;
for(auto num:nums){
if(num&z) x^=num;
else y^=num;
}
return vector<int> {x,y};
}
};数组中数字出现的次数——升级版
在一个数组
nums中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。输入：nums = [9,1,7,9,7,9,7] 输出：1
老样子，题目对于时间复杂度和空间复杂度的要求比较高，只能用位运算的方式来解决。从int型数据的二进制位角度来考虑，将数组里的数据都转化成32位二进制表示的形式，统计这32个二进制位上1出现的次数，并对3取余，做后得到的二进制数据就是数组中单独的数。
此种方法适用于所有的数组中有一个单独的数，其他的数字都出现了m次的情况，只需要按照上述步骤对m取余即可。
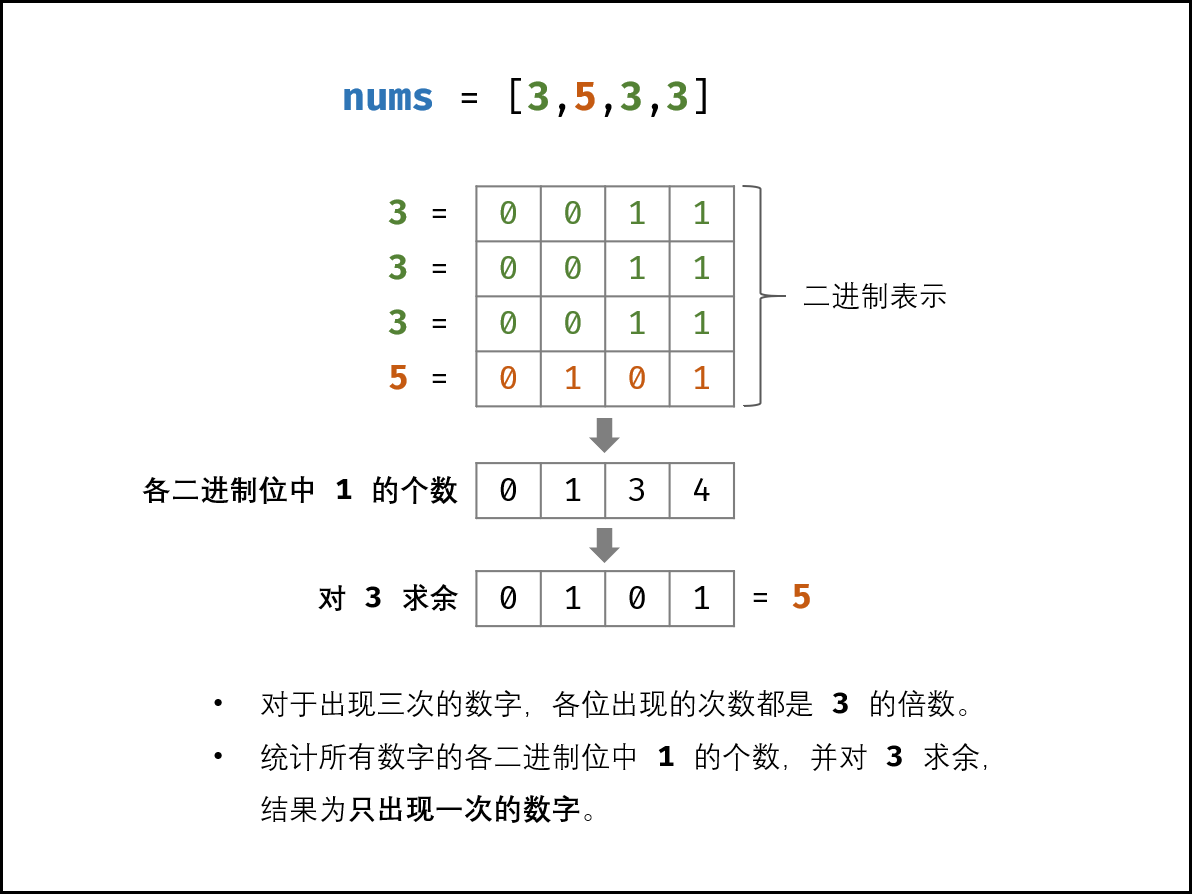
class Solution {
public:
int singleNumber(vector<int>& nums) {
vector<int> memory(32,0);
int x,res=0;
for(auto num:nums){
x=1;
for(int i=31;i>0;i--){
if(num&x) memory[i]++;
x=x<<1;
}
}
x=1;
for(int i=31;i>0;i--){
if(memory[i]%3) res+=x;
x=x<<1;
}
return res;
}
};
😈丑数——三指针法（剑指第49题）
我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。
输入: n = 10 输出: 12 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
我们知道，丑数的排列肯定是1,2,3,4,5,6,8,10.... 然后有一个特点是，任意一个丑数都是由小于它的某一个丑数*2，*3或者*5得到的，那么如何得到所有丑数呢？ 现在假设有3个数组，分别是： A：{1*2，2*2，3*2，4*2，5*2，6*2，8*2，10*2......}
B：{1*3，2*3，3*3，4*3，5*3，6*3，8*3，10*3......}
C：{1*5，2*5，3*5，4*5，5*5，6*5，8*5，10*5......}
那么所有丑数的排列，必定就是上面ABC3个数组的合并结果然后去重得到的，那么这不就转换成了三个有序数组的无重复元素合并的问题了吗？而这三个数组就刚好是{1,2,3,4,5,6,8,10....}乘以2,3,5得到的。
合并有序数组的一个比较好的方法，就是每个数组都对应一个指针，然后比较这些指针所指的数中哪个最小，就将这个数放到结果数组中，然后该指针向后挪一位。
回到本题，要求丑数ugly数组中的第n项，而目前只知道ugly[0]=1，所以此时三个有序链表分别就只有一个元素：
A ： {1*2......}
B ： {1*3......}
C ：{1*5......}
假设三个数组的指针分别是i,j,k，此时均是指向第一个元素，然后比较A[i]，B[j]和C[k]，得到的最小的数A[i]，就是ugly[1]，此时ugly就变成{1,2}了，对应的ABC数组就分别变成了：
A ： {1*2，2*2......}
B ： {1*3, 2*3......}
C ：{1*5,2*5......}
此时根据合并有序数组的原理，A数组指针i就指向了下一个元素，即'2*2'，而j和k依然分别指向B[0]和C[0]，然后进行下一轮合并，就是A[1]和B[0]和C[0]比较，最小值作为ugly[2].....如此循环n次，就可以得到ugly[n]了。
此外，注意到ABC三个数组实际上就是ugly[]*2，ugly[]*3和ugly[]*5的结果，所以每次只需要比较A[i]=ugly[i]*2，B[j]=ugly[j]*3和C[k]=ugly[k]*5的大小即可。然后谁最小，就把对应的指针往后移动一个，为了去重，如果多个元素都是最小，那么这多个指针都要往后移动一个
此题有一个注意点：三个指针的选取。一开始三个指针选取的是三个将要与 2 3 5相乘的值，但是这种做法会导致后面的判断漏掉很多数，正确的做法应该是选取索引值作为三个指针值
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> vec(n+1, 1);
int i = 1, j = 1, k = 1;
for(int a = 2; a < n+1; a++){
int num_i = vec[i] * 2, num_j = vec[j] * 3, num_k = vec[k] * 5;
int minnum = min({num_i, num_j, num_k});
vec[a] = minnum;
if(minnum == num_i) i++;
if(minnum == num_j) j++;
if(minnum == num_k) k++;
}
return vec[n];
}
};1~n整数中1出现的次数（剑指41题）
输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。
例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，‘1’一共出现了5次。
某位中 1出现次数的计算方法：
根据当前位cur值的不同，分为以下三种情况：
当cur = 0时：此位1的出现次数只由高位high决定，计算公式为：high×digit
如下图所示，以n = 2304为例，求digit = 10（即十位）的1出现次数。
当cur = 1时：此位1的出现次数由高位high和低位low决定，计算公式为:
high×digit+low+1
如下图所示，以n=2314为例，求digit=10（即十位）的1出现次数。
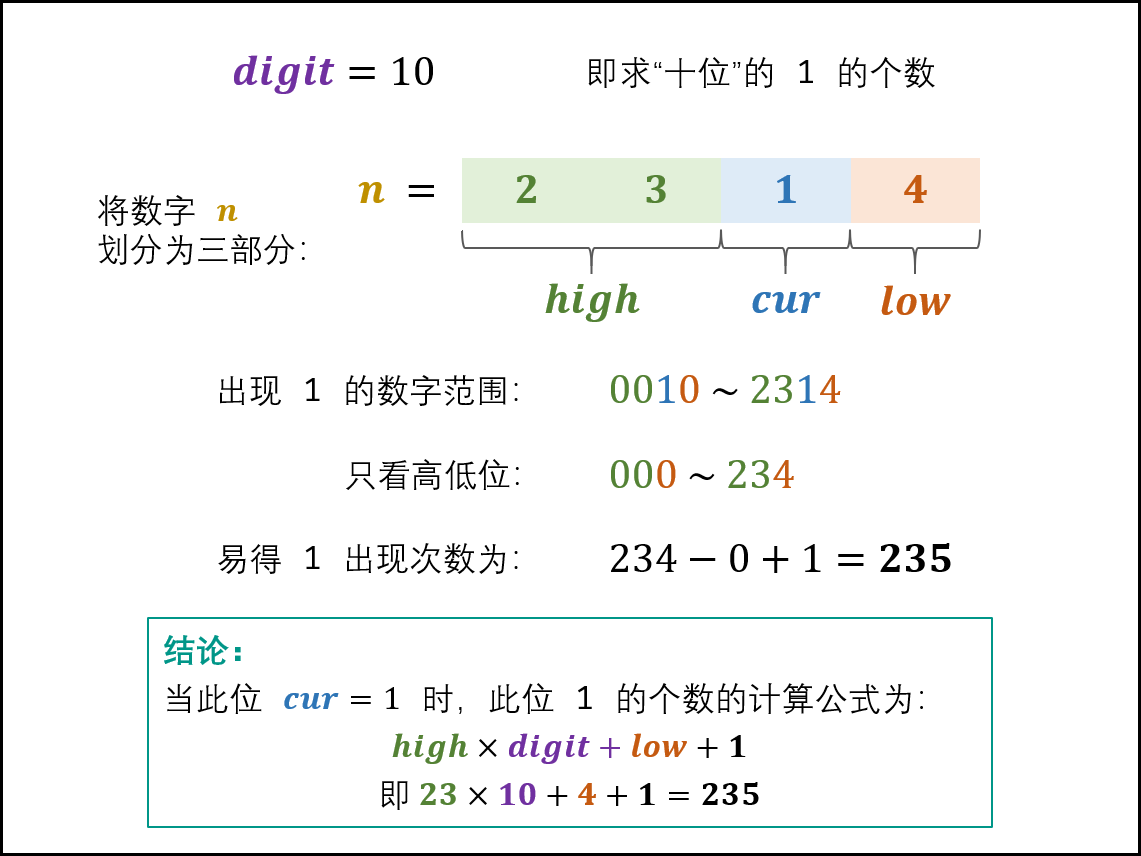
当 cur = 2, 3, 9 时： 此位1的出现次数只由高位high决定，计算公式为：(high+1)×digit
如下图所示，以n=2324为例，求digit=10（即十位的1出现次数。
class Solution {
public:
int res,length;
int countDigitOne(int n) {
string memory = to_string(n);//用字符串来取数字的高位与低位
length = memory.length();
res=0;
int high,low,digit,curr;
for(int i=0;i<length;i++){
high = i==0?0:stoi(memory.substr(0,i));
low = i==length-1?0:stoi(memory.substr(i+1,length-i-1));
digit = pow(10,length-i-1);
curr = memory[i]-'0';
if(curr==0) res += high*digit;
else if(curr==1) res += high*digit+low+1;
else res += (high+1)*digit;
}
return res;
}
};最长连续序列（第128题）——有序的数组如何避免重复遍历
给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
在一个未排序的整数数组 nums中 ，找出最长的数字连续序列
最直白的做法是：枚举nums中的每一个数x，并以x起点，在nums数组中查询x + 1,x + 2，，，x + y是否存在。假设查询到了 x + y，那么长度即为 y - x + 1，不断枚举更新答案。但题目要求时间复杂度为O(n)，为了降低时间复杂度，采用空间换取时间的策略，很容易想到用哈希表来实现。
但是如何避免重复枚举一段序列是本题的难点，我们要从序列的起始数字向后枚举。也就是说如果有一个x, x+1, x+2,,,, x+y的连续序列，我们只会以x为起点向后枚举，而不会从x+1,x+2,,,向后枚举。
其实只需要每次在哈希表中检查是否存在 x−1即可。如果x-1存在，说明当前数x不是连续序列的起始数字，我们跳过这个数。
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> num_set;
for (auto num : nums) {
num_set.insert(num);
}
int longestStreak = 0;
for (auto num : num_set) {
if (!num_set.count(num - 1)) {//本段代码的精髓
int currentNum = num;
int currentStreak = 1;
while (num_set.count(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = max(longestStreak, currentStreak);
}
}
return longestStreak;
}
};前缀和（第560题，第437题） ——求连续子数组的和
第560题
给你一个整数数组
nums和一个整数k，请你统计并返回该数组中和为k的连续子数组的个数。输入：nums = [1,2,3], k = 3 输出：2
前缀和的思想专门用于求解这类连续子数组的和的问题，遍历数组nums，将第1个，第1个加第2个，第1个加第2个加第3个........等等的求出并压入哈希表中。
如果用sum[i,j]来表示从下标i到下标j的元素的总和，那么上述操作就相当于将从sum[0,0]到sum[0,len-1]压入了哈希表，而对于sum[i,j]，只需要用下面公式就可以求出
sum[i,j]=sum[0,j]-sum[0,i]
K=sum[0,j]-sum[0,i]
在遍历的过程中判断，当前求和的值减去k得到的结果在哈希表中是否存在。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int sum=0，res=0;
unordered_map<int,int> memory;
memory[0]=1;
for(auto num:nums){
sum+=num;
if(memory.count(sum-k)) res+=memory[sum-k];//注意此句和下一句的顺序
memory[sum]++;
}
return res;
}
};第437题
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。
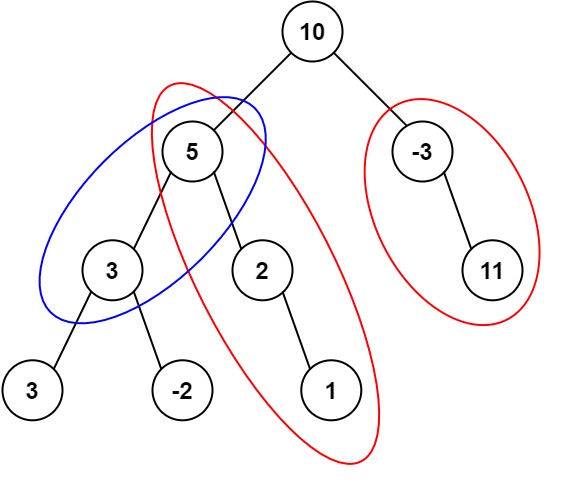
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3
解释：和等于 8 的路径有 3 条，如图所示。
如标题所言，本题解题的关键是将前缀和与深度遍历结合起来。前缀和就是二叉树中由根结点到当前结点的路径上所有节点的和。
此题一定是要用到递归的，初步考虑递归函数是计算某个节点所在树的路径和，接着将其结果与左右子树的结果相比较
对于每个节点，有两种计算的选择：
1. 计算以该节点为根节点的树的路径和
2. 计算以该节点为叶子节点的树的路径和
对于前者，当某个记诶单为根节点时，它的子节点有两种情况，这样往下遍历下去，路径和的情况有很多种，不便于分析
对于后者，一个节点的父节点有且仅有一个，计算以该节点为叶子节点时的，路径和情况唯一。
所以本题的递归函数的作用就是 计算当前节点作为叶子节点时的路径和 并且计算的顺序由上至下。
本题具体流程是用先序遍历将二叉树中每个节点的前序和，将每个前序和存入哈希表中，用于后续的查找；如果在前序遍历的过程中，发现当前点的前序和curr_sum减去题目所要的targetsum的值在哈希表中存在，那么存在一条路径，其上的节点和为targetsum，示意图如下，遍历到节点1时，发现 (curr_sum-targetsum)=(12-9)=2 在哈希表中存在，说明二叉树中存在一条路径，其上的节点的和为9。
代码的思路看起来很直白，一个前序遍历加哈希表插入和搜索即可，但在处理一些小细节时，让我吃了很多苦头，感觉还是没有养成相应的代码思维，完全是靠运行试错来完善代码。下面记录一些编写代码的注意点：
首先，此题中的哈希表采用的是unordered_map而不是unordered_set，是因为可能会出现不同节点的前缀和相等的情况，具体分析如下。
关于路径数量的统计，如果出现了 memory.count( curr_sum - targetSum ) != 0的情况，说明在而二叉树中存在节点的和为目标值，此时需要考虑到前缀和相等的情况，如下，当并遍历到节点5时，发现哈希表中有两个值，等于curr_sum减去targetsum，那么也就是对应了两条路径，4->5和 1->-1->4->5，这两条路径的值都为9。那么此时符合条件的路径数量就应该加2，即curr_sum减去targetsum的值在哈希表中数量，由此可见，应该用unordered_map来记录各个节点的前缀和。
接下来考虑深度遍历数据的压入和弹出，定义两个全局变量curr_sum和times，分别用来表示当前记诶单的前缀和和符合条件的路径条数。 前面已经确定采用前序遍历，依次将前缀和保存至哈希表中。在此过程中需要完成三步：
- 计算当前节点的前缀和
- 判断前缀和减去targetsum的值，在哈希表中是否存在
- 将前缀和插入哈希表
要注意这三步的先后顺序，如果发生颠倒，会使结果出错
接着考虑，前序遍历退出当前循环时，对于哈希表，在某个节点的左右子节点的函数都执行完，准备退出该节点时，需要在哈希表中，将该节点的前缀和删除掉，回到上一个节点的状态。
class Solution {
public:
unordered_map<long long, int> memory;
int target, res;
int pathSum(TreeNode* root, int targetSum) {
memory[0] = 1;
res = 0;
target = targetSum;
CalLength(root, 0);
return res;
}
void CalLength(TreeNode * node, long long lastsum){
if(!node) return;
long long length = lastsum + node -> val;
res += memory[length - target];
memory[length]++;
CalLength(node->left, length);
CalLength(node->right, length);
memory[length]--;
}
};
除自身以外的乘积（第238题）
给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内，即都可用int型数据表示。
要求不使用 除法 ，并且时间复杂读为O(n)，空间复杂读为常数（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）。
输入: [1,2,3,4] 输出: [24,12,8,6]
要求在常数时间复杂度里完成计算，则只能用原数组nums和输出数组res进行运算，思路是用两个数组分别表示数组中某个数左右两边的乘积。如下图
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int len=nums.size();
vector<int> res(len);
res[len-1]=1;
for(int i=len-2;i>-1;i--) res[i]=res[i+1]*nums[i+1];
for(int i=1;i<len;i++) nums[i]=nums[i-1]*nums[i];
for(int i=1;i<len;i++) res[i]=res[i]*nums[i-1];
return res;
}
};原地算法——数组索引值的运用（第448题，第645题）
对于长度为n的数组，要求它内部的元素为1~n，此题想要求出数组内部在1~n中缺失的元素（因为有重复元素的存在） 。要求时间复杂度为O(n)，除了开辟一个返回的数组，不占用额外空间。
关键：nums数组的索引值为0~n-1，总体加一正好对应题目要求的数组内范围为1~n的元素。实际上就是数组中的元素和其下标有一定的联系
解法：对于nums[i]，取abs(nums[i])-1,并对numns{abs(nums[i])-1}取负值，即标记数组中已经出现过的值，到最后数组中不为0的数的索引值即为缺失的元素。如下图
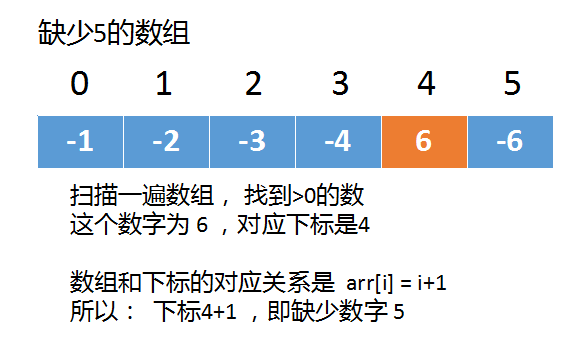
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> vec;
for(auto num:nums){
if(nums[abs(num)-1]>0)
nums[abs(num)-1]=-nums[abs(num)-1];
}
for(int i=0;i<nums.size();i++){
if(nums[i]>0)
vec.push_back(i+1);
}
return vec;
}
};集合 s 内是从 1 开始，到 n结束的整数组。不幸的是，因为数据错误，导致集合里面某一个数字复制了成了集合里面的另外一个数字的值，导致集合丢失了一个数字并且有一个数字重复 。给定一个数组 nums 代表了集合 S 发生错误后的结果。请你找出重复出现的整数，再找到丢失的整数，将它们以数组的形式返回。
示例 1： 示例 2：
输入：nums = [1,2,2,4] 输入：nums = [1,1]
输出：[2,3] 输出：[1,2]
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
int len=nums.size();
vector<int> vec;
for(int num:nums){
if(nums[abs(num)-1]>0){
nums[abs(num)-1]=-(nums[abs(num)-1]);
}
else
vec.push_back(abs(num));
}
for(int i=0;i<len;i++){
if(nums[i]>0)
vec.push_back(i+1);
}
return vec;
}
};😈乘积最大值 （力扣第152题 ）
给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
输入: [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。
输入: [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
法一：
先讨论此题的简化版：求一个整数数组中乘积最大的连续子数组，该数组中的元素不含0，只含有正数和负数，其他条件与上题相同。
讨论时分两种情况：
1.数组中负数为偶数个，则整个数组的所有元素值相乘的结果即为最大值；
2.数组中负数为奇数个，分别切除数组左右两边第一个出现负数的那一段，剩下的中间的那一段的所有元素的乘积一定为负数，此时数组整体的最大乘积就是中间那段数组的乘积与左右两边第一个的负数相乘得到的较大值（负负得正）。具体的运算过程就是从左边开始，乘到最后一个负数停止有一个“最大值”，从右边也有一个“最大值”，比较，得出最大值。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int a = 1;
int max = nums[0];
for(int num : nums){
a = a * num;
max = max > a ? max : a;
}
a = 1;
for (int i = nums.size()-1; i>=0; i--){
a = a * nums[i];
max = max > a ? max : a;
}
return max;
}
};回到本题，本题数组中存在0， 那么此时求最大值，可以看成求被0拆分的各个子数组的最大值。代码如下：
class Solution {
public:
int maxProduct(vector<int>& nums) {
int a = 1;
int max = nums[0];
for(int num : nums){
a = a * num;
max = max > a ? max : a;
if (num == 0) a = 1;
}
a = 1;
for (int i = nums.size()-1; i>=0; i--){
a = a * nums[i];
max = max > a ? max : a;
if (nums[i] == 0) a = 1;
}
return max;
}
};法二：动态规划
看到题目时就联想到用动态规划的方式处理，即创建一个长度为nums.size()的数组the_max[]，the_max[i]表示以nums[i]结尾的连续数组的乘积的最大值。遍历nums并不断更新数组the_max的值，最后返回数组the_max中的最大值。
但此种方法存在问题，当num[i]为负数时，the_max[i]的值是nums[i]前最小的负数乘以nums[i]。或者说，nums数组中包含有正数，负数和零，当前的最大值如果乘以一个负数就会变成最小值，当前的最小值如果乘以一个负数就会变成一个最大值，因此我们还需要维护一个最小值数组the_min[]。
因此，本次动态规划法需要同时维护两个动态数组，the_max, the_min。
关于两个动态数组的状态转移方程如下：(f[]表示the_max数组 g[]表示the_min数组)
the_max数组
|
|
the_min数组
|
|
可以将上述式子进行简化
代码如下：
class Solution {
public:
int maxProduct(vector<int>& nums) {
int len = nums.size();
vector<int> the_max(len),the_min(len);
int res = nums[0];
the_max[0]=res;
the_min[0]=res;
for(int i=1;i<len;i++){
if(nums[i]>-1){
the_max[i]=max(nums[i]*the_max[i-1],nums[i]);
the_min[i]=min(nums[i]*the_min[i-1],nums[i]);
}
else{
the_max[i]=max(nums[i]*the_min[i-1],nums[i]);
the_min[i]=min(nums[i]*the_max[i-1],nums[i]);
}
res = max(res,the_max[i]);
}
return res;
}
};😈移动零（第283题）
给定一个数组
nums，编写一个函数将所有0移动到数组的末尾，同时保持非零元素的相对顺序。请注意 ，必须在不复制数组的情况下原地对数组进行操作。
只能在原数组上进行操作，那么只能用双指针之类的方法，尝试过用swap函数加双指针，但是时间复杂度很高，并且边界值不好设计。参考快排的方法，过程如下所示
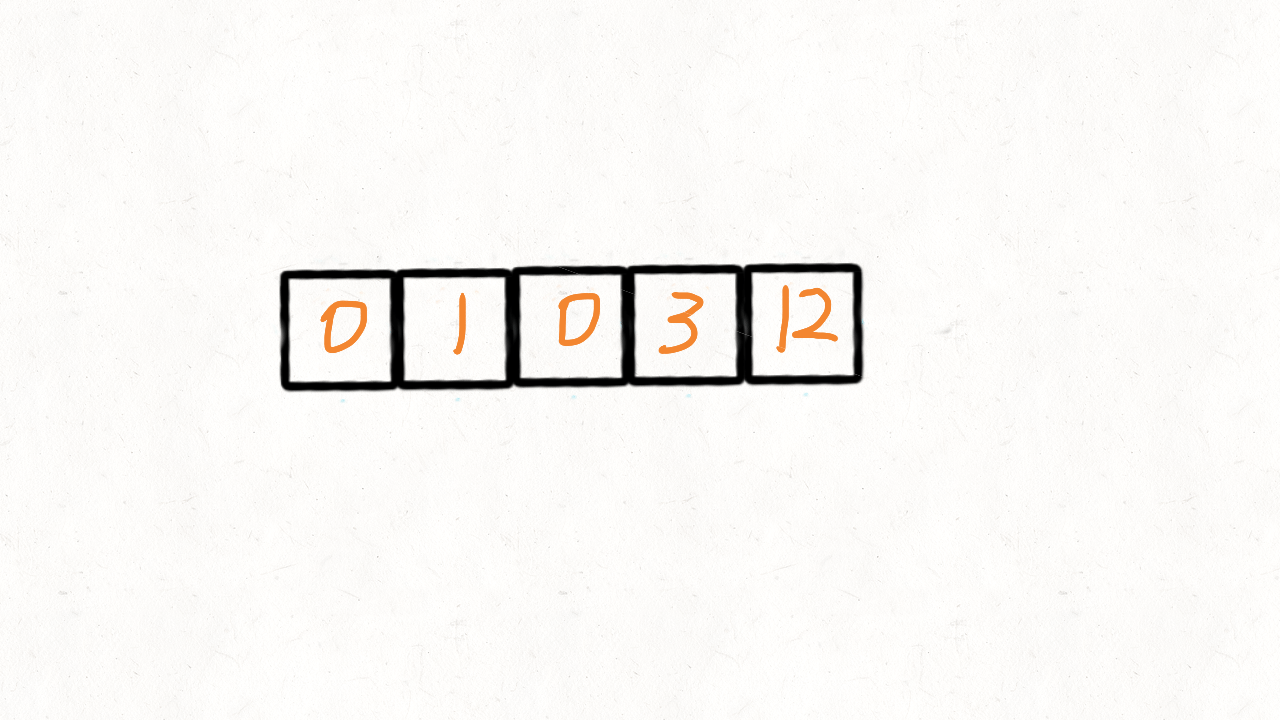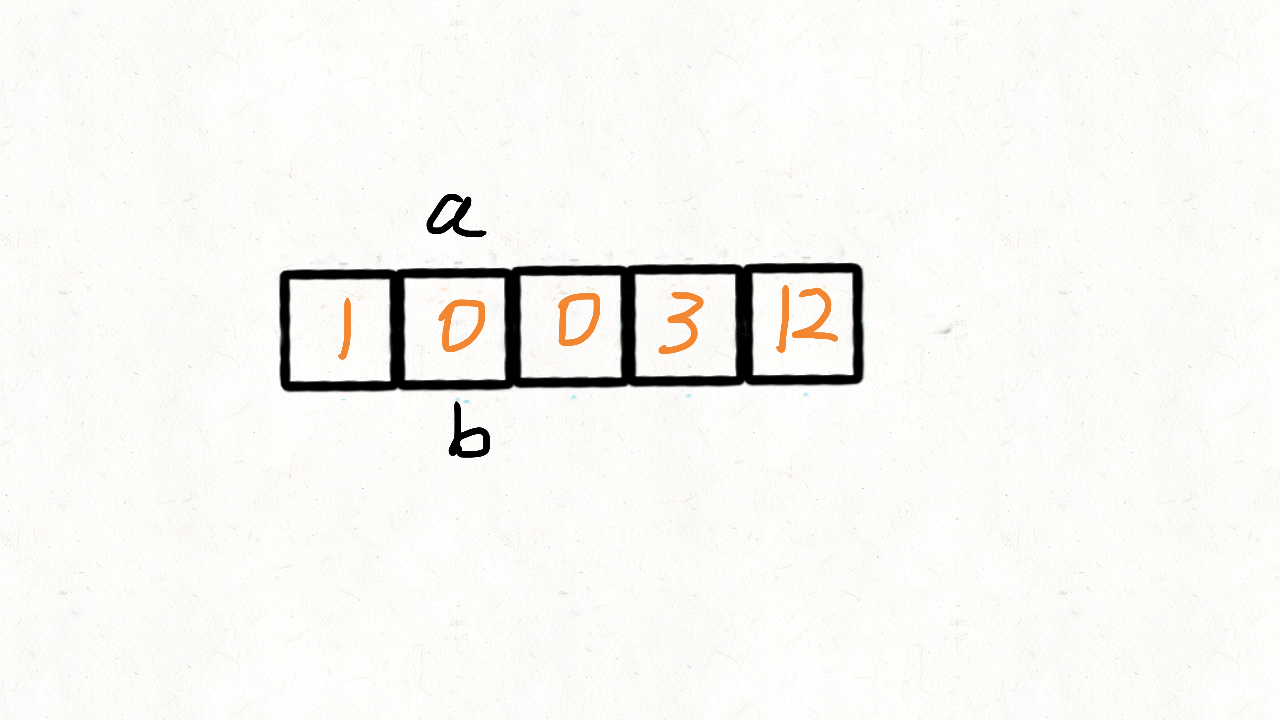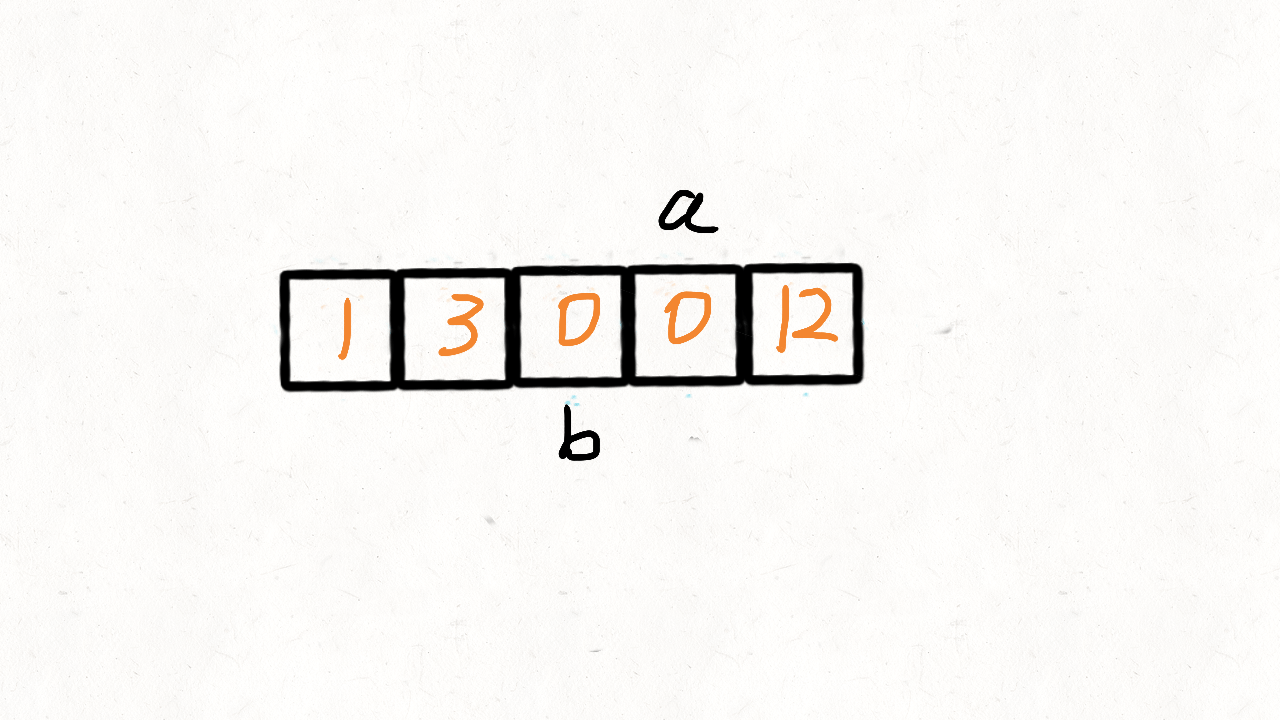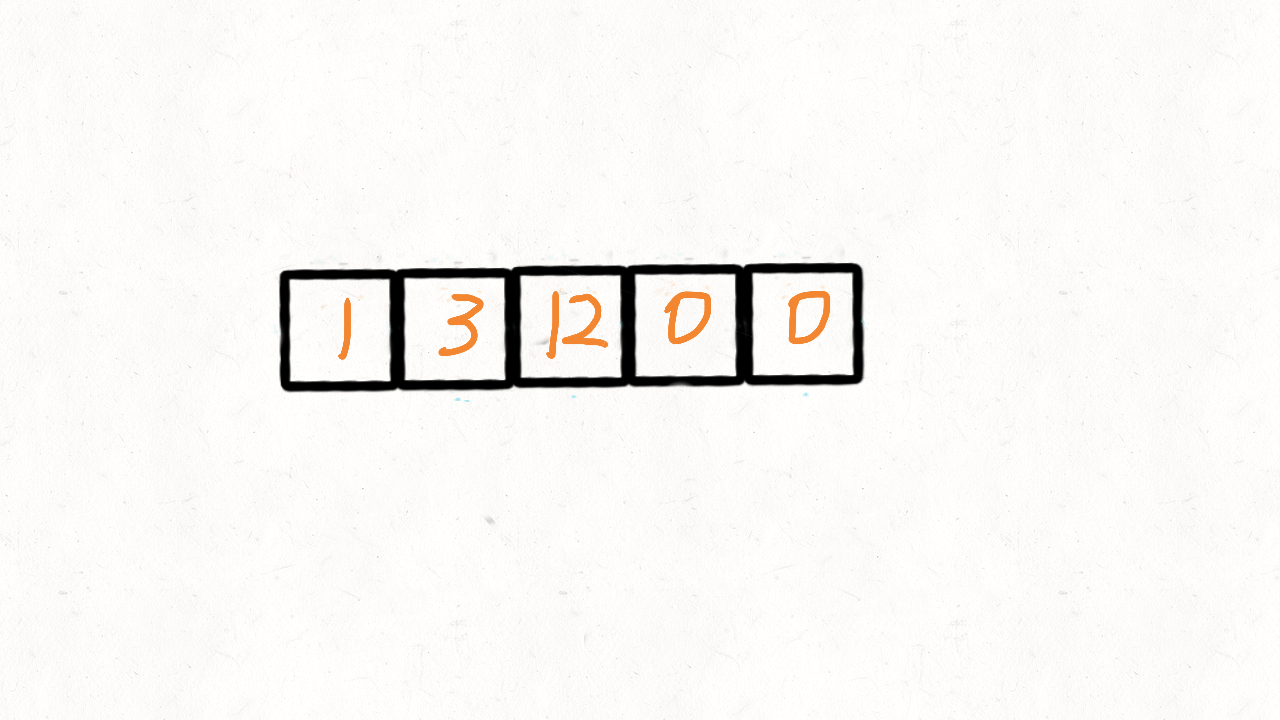
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int len = nums.size();
int j = 0;
for(int i = 0; i < len; i++){
if(nums[i] != 0){//将不等于0的都移到0的左边
if(i > j){
nums[j] = nums[i];
nums[i] = 0;
}
j++;
}
}
}
};😈构建乘积数组 （剑指66题）
给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
输入: [1,2,3,4,5] 输出: [120,60,40,30,24]所有元素乘积之和不会溢出 32 位整数
a.length <= 100000
如下图：根据表格的主对角线（全为11），可将表格分为上三角和下三角两部分。分别迭代计算下三角和上三角两部分的乘积，即可不使用除法就获得结果。
class Solution {
public:
vector<int> constructArr(vector<int>& a) {
int len = a.size();
vector<int> B_1(len, 1), B_2(len, 1);
for(int i = 1; i < len; i++){
B_1[i] = B_1[i - 1] * a[i - 1];
B_2[len - i - 1] = B_2[len - i] * a[len - i];
}
for(int i = 0; i < len; i++) B_1[i] *= B_2[i];
return B_1;
}
};其他
有向图的拓扑算法（第207题）
你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。
关于选课问题可以看成是对有向无环图的判断，即课程间规定了前置条件，但不能构成任何环路，否则课程前置条件将不成立。课程的安排可以看作是有向图，思路是通过拓扑排序判断此课程安排图是否是存在环 。
关于拓扑排序：它是用于有向无环图一个排序算法，如果一种算法可以将有向无环图中的顶点进行线性排列并输出，排序后的顶点以在图中出现的先后顺序进行排列，即对每一条有向边 (u, v)，均有 u（在排序记录中）比 v 先出现（亦可理解为对某点 v 而言，只有当 v 前面的所有源点均出现了，v 才能出现），那么这种算法可以叫做拓扑排序。
也就是说，对于有向无环图来说，对其进行拓扑排序会得到一组线性排列的正确数据，而对有向图有环图，如果对其进行拓扑排序，将得不到正确的数据，因此，可以对有向图进行拓扑排序来判断图中是否存在环。
通过bfs广度优先来进行排序
过程可以概括为：先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。重复上述操作，直到所有的节点都被分离出来，见下图。如果最后不存在入度为0的节点，那就说明有环。有向无环图在拓扑算法下，直到所有节点被分离，都一直存在入度为0的节点。而有向有环图当分离至只剩下环时，不存在入度为0的节点。
具体实现：解此题需要这样几种数据结构：
- 需要统计所有点的入度，通过vector<int>来实现
- 需要知道每个节点的，在其之后的，与它相邻的节点，如上图中的a节点，其后续的节点有b，c，d三个，考虑到后续的节点可能不止一个，用vector<int,vector<int>>来存储,也可以用unordered_map<vector<int>>，但经过测试，前者执行用时短一些
- 需要将入度为0的节点存储起来，并且随时更新，满足先入先出的顺序，用queue<int>来实现,它相对于两端队列deque，实现起来简单些。
算法流程：
1.统计课程安排图中每个节点的入度，生成入度表 indegree。
2.借助一个队列 queue，将所有入度为 0 的节点入队。
3.当 queue 非空时，依次将队首节点出队，在课程安排图中删除此节点：
- 并不是真正从邻接表中删除队首节点，而是将此节点对应所有邻接节点 的入度 -1
- 当入度 -1后，如果邻接节点的入度为 0，说明它所有的前驱节点已经被 “删除”，此时将其入队。
4.在每次queue队首节点出队时，执行 size++；
- 若整个课程安排图是有向无环图（即可以安排），则所有节点一定都入队并出队过，即完成拓扑排序。换个角度说，若课程安排图中存在环，一定有节点的入度始终不为 0。
- 因此，拓扑排序出队次数等于课程个数，返回 numCourses == size 判断课程是否可以成功安排
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> adjlst(numCourses);
vector<int> indergee(numCourses,0);
queue<int> zerodegree;
for(auto temp:prerequisites){
adjlst[temp[1]].push_back(temp[0]);//存储每个点及其相邻的点
++indergee[temp[0]];//计算入度
}
for(int i=0;i<numCourses;i++){
if(!indergee[i]) zerodegree.push(i);//将入度为0的点压入队列
}
int size=0;
while(!zerodegree.empty()){
int temp=zerodegree.front();
zerodegree.pop();//弹出队首点
for(auto num:adjlst[temp]){
--indergee[num];//将该点的相邻节点的入度减一
if(!indergee[num]) zerodegree.push(num);//如果减一后，入度为0，压入队列
}
++size;
}
return size==numCourses;
}
};
股票类问题（第121题 第122题 第309题）
第121题
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
第122题
给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
第309题
给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。输入: [1,2,3,0,2] 输出: 3 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
先看题目，股票类问题都是要求求出买卖股票所能获得最大收益。对于股票类问题，最核心并且通用的思想就是对每天的n个状态进行讨论，建立一个len*n动态数组，用动态规划的思想来解决。详见下：
对于第121题
可以直接将题目简化成为：在一个数组中，寻找两个数字，这两个数字中后者减去前者得到的结果最大。用动态规划的方法来解决，设memory[i]代表着，以prices[i]结尾的数组中两数之差的最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if(prices.size()<2) return 0;
int len=prices.size(),the_min=prices[0];
vector<int> memory(len,0);
for(int i=1;i<len;i++){
memory[i]=max(memory[i-1],prices[i]-the_min);
the_min=min(the_min,prices[i]);
}
return memory[len-1];
}
};当然，也可不用数组，而是用滚动的数字来实现。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if(prices.size()<2) return 0;
int a=0,len=prices.size(),the_min=INT_MAX;
for(int i=0;i<len;i++){
a=max(a,prices[i]-the_min);
the_min=min(the_min,prices[i]);
}
return a;
}
};以下的解法实则将问题复杂化了，但是为后面几个进阶问题提供了基础。
买卖股票机会只有一次，可以将每天的状态分为两种：手上持有股票和手上没有股票。用两个长度为prices.size()的动态数组来记录这两个状态下所能获得的最大收益，当然，更为简便的表示方法是建立一个二维数组：vector<vector<int>> dp(len,vector<int>(2,0))；其中dp[i][0]表示第i天结束时，如果手上不持有股票，所拥有的金额数；dp[i][1]表示第i天结束时，如果手上持有股票，所拥有的金额数.
这样就能很方便的写出状态转移方程了：
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], -prices[i])第i天结束时，如果手上没有股票，那么会有两种情况：前一天手上有股票，今天给它卖了；之前就已经把股票买了，现在手上的一直是之前卖股票所得的。
即第i天结束时，如果手上持有股票，那么此时有两种情况：前一天手上有股票，今天还是没有买；前一天没有股票，今天买了一个股票。
初始化时
dp[0][0] = 0;
dp[0][1] = -prices[0];当然，进一步研究发现，其实不需要动态数组，用两个滚动的数字也可以完成
int a=0;
int b=-prices[0];
a = max(a, b + prices[i]);
b = max(b, -prices[i])代码如下：
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.size();
if (len < 2) return 0;
int a=0;
int b=-prices[0];
for (int i = 1; i < len; i++) {
a = max(a, b + prices[i]);
b = max(b, -prices[i])
}
return a;
}
}
对于122题，与121题类似，建立一个二维数组：vector<vector<int>> dp(len,vector<int>(2,0))；略有不同的是，其中dp[i][0]表示第i天结束时，如果手上不持有股票，所拥有的最大金额数；dp[i][1]表示第i天结束时，如果手上持有股票，所拥有的最大金额数.
列出对应的状态方程：
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);此题中的股票可以多次买卖，所以状态方程略有不同。
第i天结束时，如果手上没有股票，那么对于今天所获得的最大金额数，会有两种情况：
- 前一天手上有股票，今天给它卖了，那么今天的收入就是昨天手上有股票时的收入加上今天卖掉股票收获的的收入（dp[i - 1][1] + prices[i]）；
- 昨天手上就已经没有股票，今天还是一样，今天的收入与昨天相同（dp[i - 1][0]）。
第i天结束时，如果手上持有股票，那么对于今天所获得的最大金额数，有两种情况：
- 前一天手上有股票，今天还是没有卖，今天的收入与昨天相同（dp[i - 1][1]）；
- 前一天没有股票，今天买了一个股票，那么今天的收入就是昨天手上没有股票时的收入加上今天买掉股票收获的的收入（dp[i - 1][0] - prices[i]）。
相似的，此状态方程也可以用几个滚动的数来完成。
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.size();
if (len < 2) return 0;
int cash = 0;
int hold = -prices[0];
for (int i = 1; i < len; i++) {
int preCash = cash;
int preHold = hold;
cash = max(preCash, preHold + prices[i]);
hold = max(preHold, preCash - prices[i]);
}
return cash;
}
}第309题，此题与上面两题不同，此题中增加了冷冻期的状态，即今天卖出股票后，明天不能买入股票，但如果今天买入股票了，明天依旧能卖出股票。此题我是将一天的状态分成了四种，判断的标准不再是是否持有股票，而是是否买卖股票：
这四种状态分别为：
第i天结束时，买入一支股票；
第i天结束时，卖出一支股票；
第i天结束时，因为前一天卖出了股票，所以今天不能操作，为已卖不买；
第i天结束时，前一天已经买了一支股票，但今天选择不做操作，股票仍留在手里，为已买不卖。
这样代码就很好写了：
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len=prices.size();
int a=0,b=-prices[0],c=0,d=b;
int res=0;
for(int i=1;i<len;i++){
int a1=a,b1=b;
a=max(prices[i]+b,d+prices[i]);
b=c-prices[i];
c=max(a1,c);
d=max(d,b1);
res=max(max(a,b),max(c,d));
}
return res;
}
};并查集（第399题）
给你一个变量对二维数组 equations 和一个实数值数组 values 作为已知条件，
其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
现给出数组 queries，其中 queries[j] = [Cj, Dj]，请根据已知条件找出 Cj / Dj 的结果作为答案。返回所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。
注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果
输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]
该问题实际上就是已知有多个变量，然后每个变量之间都有倍数关系，要求其他一些变量的倍数关系。由此可以联系到图论上，equations中的元素即图中的顶点，而values中给出的不同元素的比值就是图中不同顶点之间的权值。在图结构汇中需要区分子节点和父节点，在此题中将分母作为父节点，分子作为子节点，而分子与分母的比值就是从子节点到父节点的权重值。
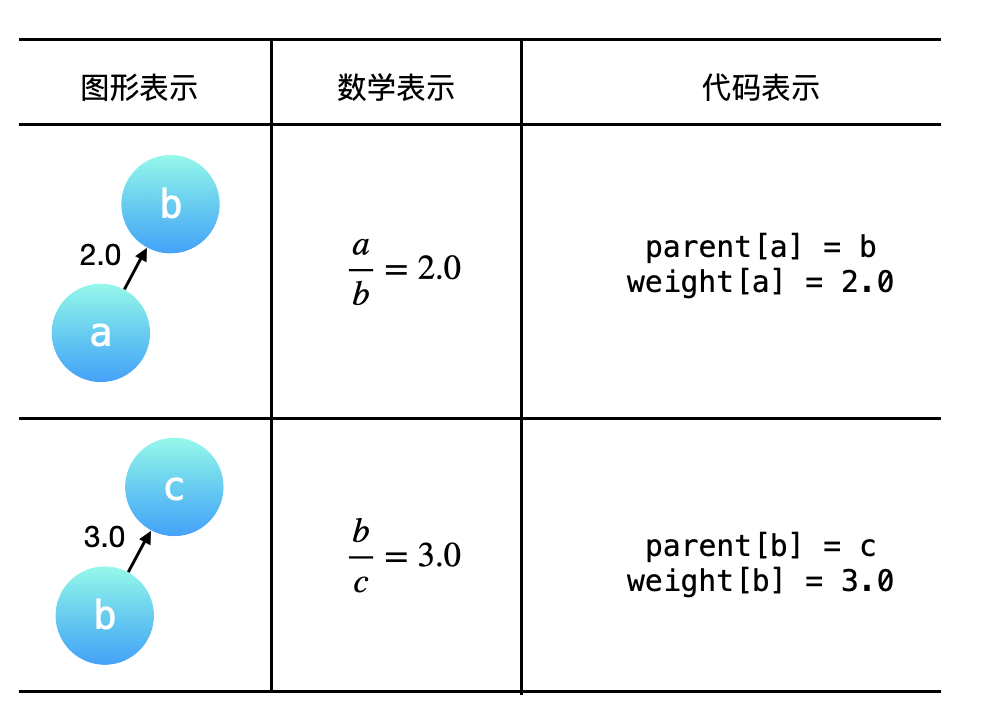
如果能将有倍数关系的子节点都连接到同一个父节点上，那么这些子节点之间的倍数关系也就能求出。如下，此题的解法就是根据equations和values中的信息构建图结构，而如果想一组链式子节点变成树状结构图，指向同一个父节点，需要用到并查集的知识。并查集是一种算法，主要作用就是将不同的树状结构合并到一起，它主要通过维护一个存储父节点的动态数组来不断改变节点之间的关系。
并查集算法由find，merge，make三个函数构成，在本题中，由于equations 中的元素已经给出，并且这些元素一定有倍数关系，所以本题中只需要用find和merge函数，其中用merge函数将equations中的元素一对一对合并，find函数的作用是找到当前节点的父节点。本题还会用到几个数据结构，其中unordered_map <string,int> variables将equations中的字符元素转换为数字编号，vector数组f(father)存储父节点，f[i]=j代表编号为i的节点的父节点编号为j；vector数组w(weight)存储当前节点到其根节点的总倍数关系值.以下两图分别表示find和merge函数中的权值计算方法。
class Solution {
public:
int findf(vector<int>& f, vector<double>& w, int x) {
//寻找当前节点的父节点并返回 参数x指的是当前节点的代号
if (f[x] != x) {//如果出现f[x]==x, 证明该节点是根节点，直接返回
int father = findf(f, w, f[x]);
w[x] = w[x] * w[f[x]];//更新权值 f数组实时更新 通过递归不断更新节点状态
f[x] = father;
}
return f[x];
}
void merge(vector<int>& f, vector<double>& w, int x, int y, double val) {
//合并 这一步是直接合并而不需要判断
//相当于人为的选出了需要合并的节点人后直接执行这段语句
int fx = findf(f, w, x);
int fy = findf(f, w, y);
f[fx] = fy;
w[fx] = val * w[y] / w[x];//关键语句
}
vector<double> calcEquation(vector<vector<string>>& equations,
vector<double>& values,
vector<vector<string>>& queries) {
int nvars = 0;
unordered_map<string, int> variables;
//存储各个节点并将其用代号一一对应，每个节点只出现一次
int n = equations.size();
for (int i = 0; i < n; i++) {
if (variables.find(equations[i][0]) == variables.end()) {
variables[equations[i][0]] = nvars++;
}
if (variables.find(equations[i][1]) == variables.end()) {
variables[equations[i][1]] = nvars++;
}
}//给元素编号
vector<int> f(nvars);//父节点 father
vector<double> w(nvars, 1.0);//权值 weight
for (int i = 0; i < nvars; i++) {
f[i] = i;
}
for (int i = 0; i < n; i++) {
int va = variables[equations[i][0]];
int vb = variables[equations[i][1]];
merge(f, w, va, vb, values[i]);//将数据存入
}
vector<double> ret;
for (const auto& q: queries) {
double result = -1.0;//若哈希表中没有该节点 直接返回-1
if (variables.find(q[0]) != variables.end()
&& variables.find(q[1]) != variables.end()) {
int ia = variables[q[0]], ib = variables[q[1]];
//得到 queries 中字符在 variables 中对应的代号
int fa = findf(f, w, ia), fb = findf(f, w, ib);
if (fa == fb) {//如果对应的父节点相同
result = w[ia] / w[ib];
}
}
ret.push_back(result);
}
return ret;
}
};接雨水（力扣42题）
给定
n个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）
本题的关键是按列求取，即求每一列所能存储雨水的数量。
对于每一个柱子，只要该柱子的左边右边都存在比其高的柱子，则在该柱子上无法存储雨水，只有当柱子的两边都存在比其大的柱子，才能存储雨水，并且在该柱子上储存雨水的多少由左右两边柱子中的较小值决定。
代码需要求出对于每一个柱子，它的左边和右边最高的柱子的高度，分别存储在两个数组中，如果某个柱子左右都存在比它高的柱子，那么此柱可接雨水量为0。
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
// left[i]表示height[i]左边的最大值，right[i]表示height[i]右边的最大值
vector<int> left(n), right(n);
for (int i = 1; i < n; i++) {
left[i] = max(left[i - 1], height[i - 1]);
}
for (int i = n - 2; i >= 0; i--) {
right[i] = max(right[i + 1], height[i + 1]);
}
int water = 0;
for (int i = 0; i < n; i++) {
int level = min(left[i], right[i]);
water += max(0, level - height[i]);
}
return water;
}
};柱状图中最大的矩形（力扣第84题）
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积
输入：heights = [2,1,5,6,2,3] 输出：10 解释：最大的矩形为图中红色区域，面积为 10
此题与上一题接雨水一样，还是柱状图问题，关于此类题目一个比较重要的思考角度就是按列解决。
对于此题，就是求对于柱状图中每一列，将其包含在内的矩形的最大值。然后再在这一系列矩形最大值中找出最大的。所以本题的关键就是如何求出包含某一列的矩形的最大值，该矩形的高度就是此列的高度。观察上图可知，对于柱状图中的任意一列，如果它的两边的柱状图都比它大，那么包含该列的矩形就能向两侧扩展，而如果只有一侧的柱形比它大，那么矩形只能向那一侧延伸，而如果该列的两侧都没有比它大的柱，那么包含该柱的最大矩形就是该柱本身。
进一步可知，此题的关键是对于每一个柱，找出它左侧和右侧第一个比它小的柱，并且此题要求的是矩形的面积，所以应该找的是第一个比其小的柱的下标值，以方便计算宽度。
要求第一个比xxx小的数，首先想到的就是单调栈，构建一个单调栈，单调栈中存放元素的下标值，栈中按下标值对应元素的大小由小到大排列，即栈顶元素始终是栈中最大的元素，当有元素要入栈时，如果栈顶元素小于等于该元素，则直接入栈；否则不断将栈内元素弹出，直到栈为空或栈顶元素小于等于待入栈元素，此时再将元素压入栈。
如上图，单调栈中存储的是下标值，括号里是下标值对应的heights数组中的值。可以看到单调栈元素按数组中的实际由小到大排列。当新元素heights[5]要插入时，因为栈顶元素大于待压入元素，所以要将栈顶元素进行出栈，而在出栈时，该元素对应的柱所能构建的矩形就已经确定了。
首先，该柱，在本例中是heights[4]，它右边第一个比它小的元素就是待入栈元素height[5]，而单调栈中的元素又是按元素实际大小由小到大排列的，所以heights[4]左边第一个比它大的数就是单调栈中它的前一个元素heights[2]。这样就能得到以heights[4]为高度构建的矩阵的宽度了。
特殊的，如果出栈时。某元素是栈中最后一个元素，那就说明，在数组中，它的左边没有比它大的，那么包含该柱的矩形就能一直向左延伸，同理，当数组中的所有元素都压入栈之后，栈中如果存在元素，那么此时栈中的栈顶元素对应的数组中的元素，该元素对应柱的右边全是大于等于它的柱，以它为基础的矩形就能一直向右延伸。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int res = 0;
int len = heights.size();
stack<int> memory;
int length = 0, height = 0;
for (int i = 0; i < len; i++) {
while (!memory.empty() && heights[memory.top()] > heights[i]){
height = heights[memory.top()];
memory.pop();
length = memory.empty() ? i : i - memory.top() - 1;
res = max(res, length * height);
}
memory.push(i);
}
while (!memory.empty()){
height = heights[memory.top()];
memory.pop();
length = memory.empty() ? len : len - memory.top() - 1;
res = max(res, length * height);
}
return res;
}
};针对上面解法进行优化，在数组的头尾分别加入一个哨兵，其值为0，即比任何一个柱都要小；
头部的0是为了不用判断栈是否为空，因为题目中都是非负整数，所以没有数会比0小，即0一直会在栈底。
尾部的0是为了压出最后已经形成的单调栈的， 比如说示例: 2,1,5,6,2,3 遍历完之后单调栈中还剩余[1,2,3]，此时在压入一个元素0，就可以把遍历完单调栈[1,2,3]给压出来。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int len = heights.size();
if (len == 0) return 0;
if (len == 1) return heights[0];
int res = 0;
heights.insert(heights.begin(), 0);
heights.push_back(0);
stack<int> memory;
//int length = 0, height = 0;
memory.push(0);
for (int i = 1; i < len + 2; i++) {
while (heights[memory.top()] > heights[i]){
int height = heights[memory.top()];
memory.pop();
int length = i - memory.top() - 1;
res = max(res, length * height);
}
memory.push(i);
}
return res;
}
};进阶：最大矩形（力扣85题）
给定一个仅包含
0和1、大小为rows x cols的二维二进制矩阵，找出只包含1的最大矩形，并返回其面积。如下，输出6.
此题是上一题的的延伸，如下图所示，实际上就是求多个数表示的柱状图中的最大值。
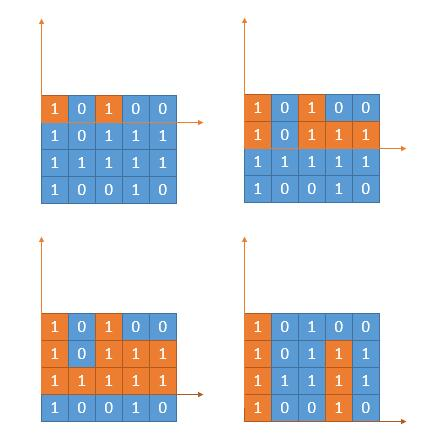
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int row = matrix.size(), column = matrix[0].size();
vector<int> the_row(column+2, 0);
for (int j = 0; j < column; j++) if(matrix[0][j] == '1') the_row[j+1] = 1;
int res = findMax(the_row);
for (int i = 1; i < row; i++){
for(int j = 0; j < column; j++){
if(matrix[i][j] == '0') the_row[j+1] = 0;
else if(matrix[i-1][j] == '1') the_row[j+1]++;
else the_row[j+1] = 1;
}
res = max(res, findMax(the_row));
}
return res;
}
int findMax(const vector<int> & the_row){
int res = 0;
stack<int> memory;
memory.push(0);
for (int i = 1; i < the_row.size(); i++){
while (the_row[i] < the_row[memory.top()]){
int height = the_row[memory.top()];
memory.pop();
int length = i - memory.top() -1;
res = max(res, height * length);
}
memory.push(i);
}
return res;
}
};递归
升序数组转二叉搜索树（力扣第108题）
贴代码
递归算法 （太经典了）
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) :
* val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return sort(nums,0,nums.size()-1);//因为要用到递归调用，所以将函数封装
}
TreeNode* sort(vector<int>& nums,int low,int high){
if(low>high){
return nullptr;//退出sort函数，不再执行下面的语句，此时到达了数组的边缘，
//即二叉树的叶节点
}
int mid=(low+high)/2;
TreeNode *root=new TreeNode(nums[mid]);
root->left=sort(nums,low,mid-1);
root->right=sort(nums,mid+1,high);//向下延伸子节点
return root;//递归算法有先进后出的现象在里面，最先返回的是叶节点指针值，最后返回的是
//根节点的指针值
}
};递归算法运行时，下图可看作示意图（虽然是归并算法的图，里面的数据对应不上，不过意思到了就行😂👌）
二叉树类的递归程序中，每次递归都会返回一个节点的指针值，因此递归算法的输入数据不需要节点指针。
递归三部曲：
- 确定递归函数返回值及其参数
删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成， 本题要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子。
再来看参数，首先是传入数组nums，然后就是左下表left和右下表right
- 确定递归终止条件
这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了。
- 确定单层递归的逻辑
首先取数组中间元素的位置，int mid = (left + right) / 2;
这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！所以可以这么写：int mid = left + ((right - left) / 2);
但本题leetcode的测试数据并不会越界，所以怎么写都可以。但需要有这个意识！
取了中间位置，就开始以中间位置的元素构造节点，代码：TreeNode* root = new TreeNode(nums[mid]);接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点；最后返回root节点。
栈的逆序化
给一个栈，请逆序这个栈。不能申请额外的数据结构，只能使用递归求解。
这道题难点就在于无法申请额外数据结构，可以用两个递归函数实现；
第一个递归函数get_and_remove_last()主要用途是将栈底的数据弹出栈，栈中其他位置的值保持不变，并返回原栈底数据的值，所以我们可以使用递归让栈内的数据依次出栈，直到最后一个数据出栈后栈为空，返回该数据的值，递归开始往回走，让之前出栈的值再依次进栈。
第二个递归函数Reverse()负责将栈逆序，这就需要我们开始调用get_and_remove_last()函数将栈中数据出栈，直到栈为空，此时最后一个出栈的一定是栈顶数据，这时递归就要往回走，我们只需要将出栈的数据依次再压入栈中即可，此时先入栈的是最后一个出栈的栈顶，最后一个入栈的就是之前的栈底，这样就完成了逆序。
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int get_and_remove_last(stack<int>& s){
int temp = s.top();
s.pop();
if (s.empty()) return temp;
int last = get_and_remove_last(s);
s.push(temp);
return last;//在多次递归过程中，last保持不变，它负责将栈底元素传送到函数的入口处并返回
}
void reverse(stack<int> &s){
if (s.empty()) return;
int temp = get_and_remove_last(s);
reverse(s);
s.push(temp);
}
int main() {
stack<int> s;
for (int i = 0; i < 5; i++) s.push(i);
reverse(s);
while (!s.empty()){
cout << s.top() << " ";
s.pop();
}
cout << endl;
return 0;
}汉诺塔问题
在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。你需要原地修改栈。
提示: A中盘子的数目不大于14个。
示例1: 输入：A = [2, 1, 0], B = [], C = [] 输出：C = [2, 1, 0]
假设 n = 1,只有一个盘子，很简单，直接把它从 A 中拿出来，移到 C 上；
如果 n = 2 呢？这时候我们就要借助 B 了，因为小盘子必须时刻都在大盘子上面，共需要 4 步。
如果 n > 2 呢？思路和上面是一样的，我们把 n 个盘子也看成两个部分，一部分有 1 个盘子，另一部分有 n - 1 个盘子。
此时考虑将n - 1 个盘子是从 A 移到 C ，这其实就是重复上面的过程，直到n的个数为1.
如果原问题可以分解成若干个与原问题结构相同但规模较小的子问题时，往往可以用递归的方法解决。具体解决办法如下：
n = 1 时，直接把盘子从 A 移到 C；
n > 1 时，
- 先把上面 n - 1 个盘子从 A 移到 B（子问题，递归）；
- 再将最大的盘子从 A 移到 C；
- 再将 B 上 n - 1 个盘子从 B 移到 C（子问题，递归）。
class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
int n = A.size();
move(n, A, C, B);
}
void move(int n, vector<int> &begin, vector<int> &end, vector<int> &mid){
if(n == 1) {
end.push_back(begin.back());
begin.pop_back();
return;
}
move(n-1, begin, mid, end);
end.push_back(begin.back());
begin.pop_back();
move(n-1, mid, end, begin);
}
};
扫一扫
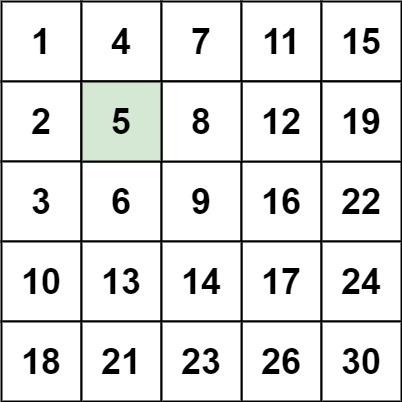
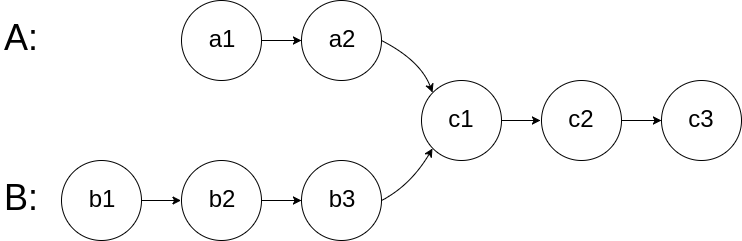
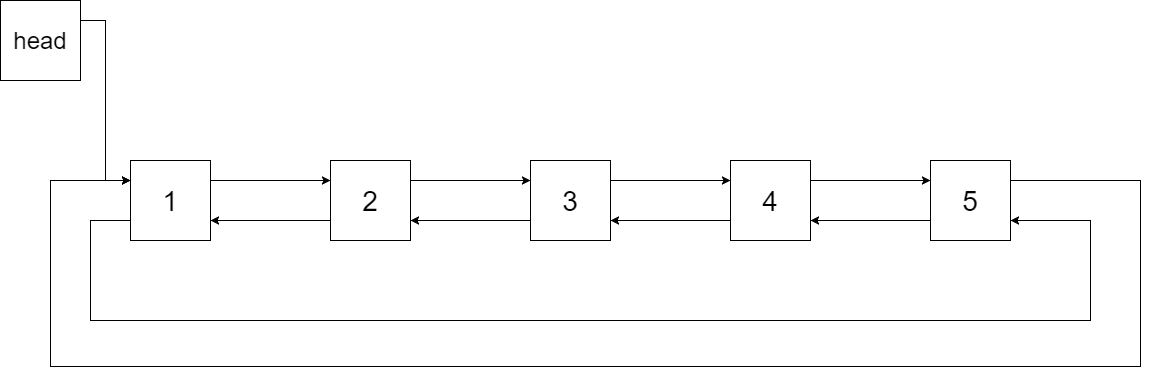
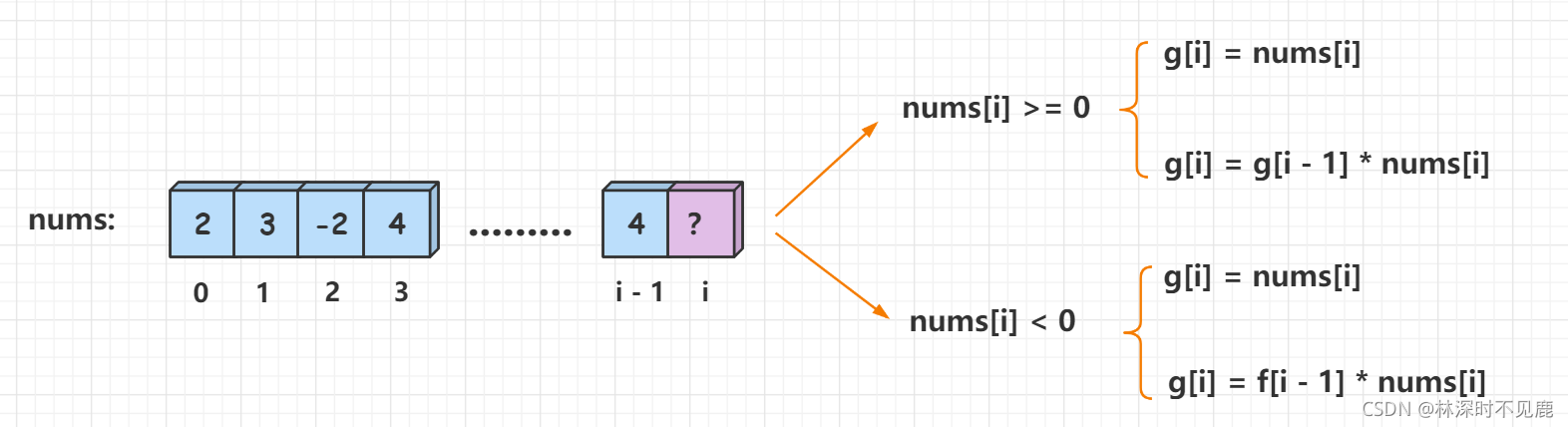
1660
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
