LeetCode 1191-K次串联后最大子数组之和

预备知识

最大子数列问题：在一维数列中找到一个连续的子数列，使该子数列的和最大。

对于该问题有一个基于动态规划的经典算法： $\text{Kadane}$ 算法。该算法使用 maxOfEnd 表示以当前数组元素结尾的最大子数列和，转移过程也十分简单——要么就是只取当前元素，要么就是拖家带口把前一元素的 maxOfEnd 一起带上。

若 $arr=[5,7,-3,2,9,6,16]$，假设子数列在索引 $2$ 处开始，$arr[2]=-3$，然后到索引 $3$，连续子数列和为 $-3+2=-1$。如果子数列在索引 $3$ 处开始，那么此时子数列和为 $2$，大于前一个子数列和。

所以我们有两种选择：在当前索引处开始 或者 将当前值加入前一个子数列和。由于我们想要最大子数列和，所以当前一个子数列和小于 $0$ 时，我们将当前值加上 $0$，否则将当前值加上前一个子数列和。
$$dp[i]=max(dp[i-1],0)+arr[i]\forall i\in [1,n-1]$$

对于上述示例，我们可以使用以下的 $\text{Kadane}$ 算法计算：

int largestSubarraySum(int[] arr){
	int maxOfEnd, maxSoFar;
	maxSoFar = maxOfEnd = arr[0] > 0 ? arr[0] : 0;
	for(int i = 1; i < arr.length; i++){
		maxOfEnd = Math.max(maxOfEnd + arr[i], arr[i]);		//记录以当前数组元素结尾的最大子数列和
		maxSoFar = Math.max(maxOfEnd, maxSoFar);			//记录当前子数列和中最大值
	}
	return maxSoFar;
}

方法一：动态规划

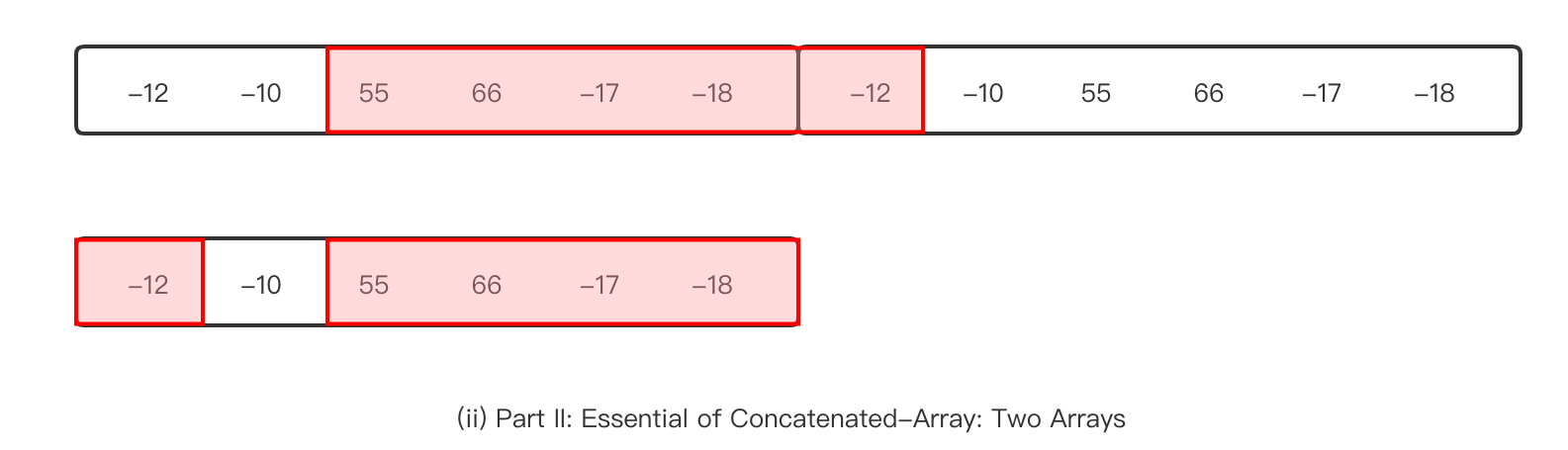
回到问题本身，由于数组可以重复出现，所以实际上，我们的子数组是可以跨过原始数组 arr 的边界的。如果我们限制子数组长度在 arr.length 以内，那么问题将转变为 “最大子数组和” 的变种，即子数组可以是以下两种形式：

• 常规型：就是通常意义的子数组。formal(i,j) 定义为：arr[i] + arr[i+1] + ... + arr[j]，其中 0 <= i <= j < arr.length。
• 非常规型：这种子数组分为两段，第一段为原始数组的首元素开始，第二段以原始数组的末元素结尾。nonformal(i,j) 定义为：arr[0] + arr[1] + ... + arr[i] + arr[j] + arr[j+1] + ... + arr[arr.length-1]，其中 0 <= i <= j < arr.length。

上面这个变种问题，我们可以通过下面算法来解决：我们准备两个 arr，然后对它执行 $\text{Kadane}$ 算法，这样我们得到的结果一定涵盖了上面两种类型的子数组。

int largestSubarraySum(int[] arr) {
  int maxOfEnd, maxSoFar, len = arr.length;
  maxSoFar = maxOfEnd = arr[0] > 0 ? arr[0] : 0;
  for (int i = 1; i < len * 2; i++) {
    maxOfEnd = Math.max(maxOfEnd + arr[i % len], arr[i % len]);
    maxSoFar = Math.max(maxOfEnd, maxSoFar);
  }
  return maxSoFar;
}

上面算法给出的结果为如下图红色部分，为什么呢？

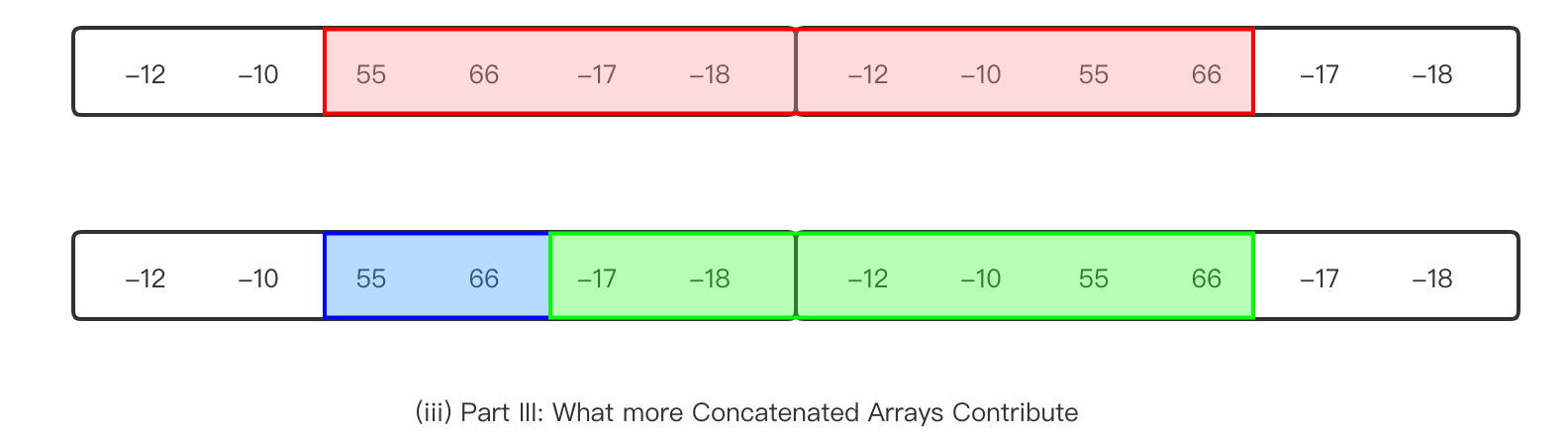
我们把结果分成两部分：蓝色和绿色。可以看出，这是一个常规性的子数组（蓝色）加上一个完整的原始数组 arr 得到的。[55,66] 是所有常规和非常规子数组中最大的，但是因为 sum(arr) > 0，所以它还可以被扩展一个 arr.length 的长度。因此，我们可以得出最后的算法，如果 sum(arr) > 0，maxSoFar 可以反复叠加 k - 2 次 sum(arr)。k==1 的边界条件需要小心处理。

class Solution {
    public int kConcatenationMaxSum(int[] arr, int k) {
        if(arr == null || arr.length == 0)
            return 0;
        long maxOfEnd = arr[0] > 0 ? arr[0] : 0L, maxSoFar = maxOfEnd, sum = arr[0];
        for(int i = 1; i < Math.min(k, 2) * arr.length; i++){
            maxOfEnd = Math.max(maxOfEnd + arr[i % arr.length], arr[i % arr.length]);
            maxSoFar = Math.max(maxOfEnd, maxSoFar);
            if(i < arr.length)                              //求数组的和
                sum += arr[i];
        }
        while(sum > 0 && --k >= 2)
            maxSoFar = (maxSoFar + sum) % 1000000007;
        return (int) maxSoFar % 1000000007;
    }
}

注意
为什么 i < Math.min(k, 2) * arr.length ？即若 k >= 2 时，要算 2 个数组的最大连续子数列和，而不能只算 1 个再叠加 k - 1 个 sum(arr)。

假设数组 arr = [1, -2, 1], k = 2，此时若只算 1 个数组的最大连续子数列和，那么 maxSoFar = 1，而 sum(arr) = 0，所以最终结果为 1。但我们可以知道 [1, -2, 1, 1, -2, 1] 中 [1, 1] 是最大连续子数列和，所以结果有误，必须要考虑上结尾和开头结合的这种情况。

进一步证明
定义：数组 arr 的所有元素之和为 sum(arr)，arr 重复 k 次表示为 carr(k)（k >= 2）。那么 carr(k) 中所有的子数组可以写为：

• formal(i, j) + carr(n)，其中 n = 0, 1, 2, ..., k - 1 并且 0 <= i <= j <= len(arr) - 1
• nonformal(i, j) + carr(m)，其中 m = 0, 1, 2, ..., k - 2 并且 0 <= i <= j <= len(arr) - 1

显然，sum(arr) <= 0 时，所有长度超过 len(arr) 的子数组不可能比 formal(i, j) 和 nonformal(i, j) 中的最大子数组大。而当 sum(arr) > 0 时：

• formal(i, j) + carr(n) 之和可以写成 sum(formal(i, j)) + sum(arr) + r * sum(arr)
• nonformal(i, j) + carr(m) 之和可以写成 sum(nonformal(i, j)) + r * sum(arr)

这里，0 <= r <= k - 2。所以问题的关键就在于求出 sum(formal(i, j)) + sum(arr) 和 sum(nonformal(i, j)) 的最大值，而这个问题恰恰用 carr(2) 的 $\text{Kadane}$ 算法就可以求解。

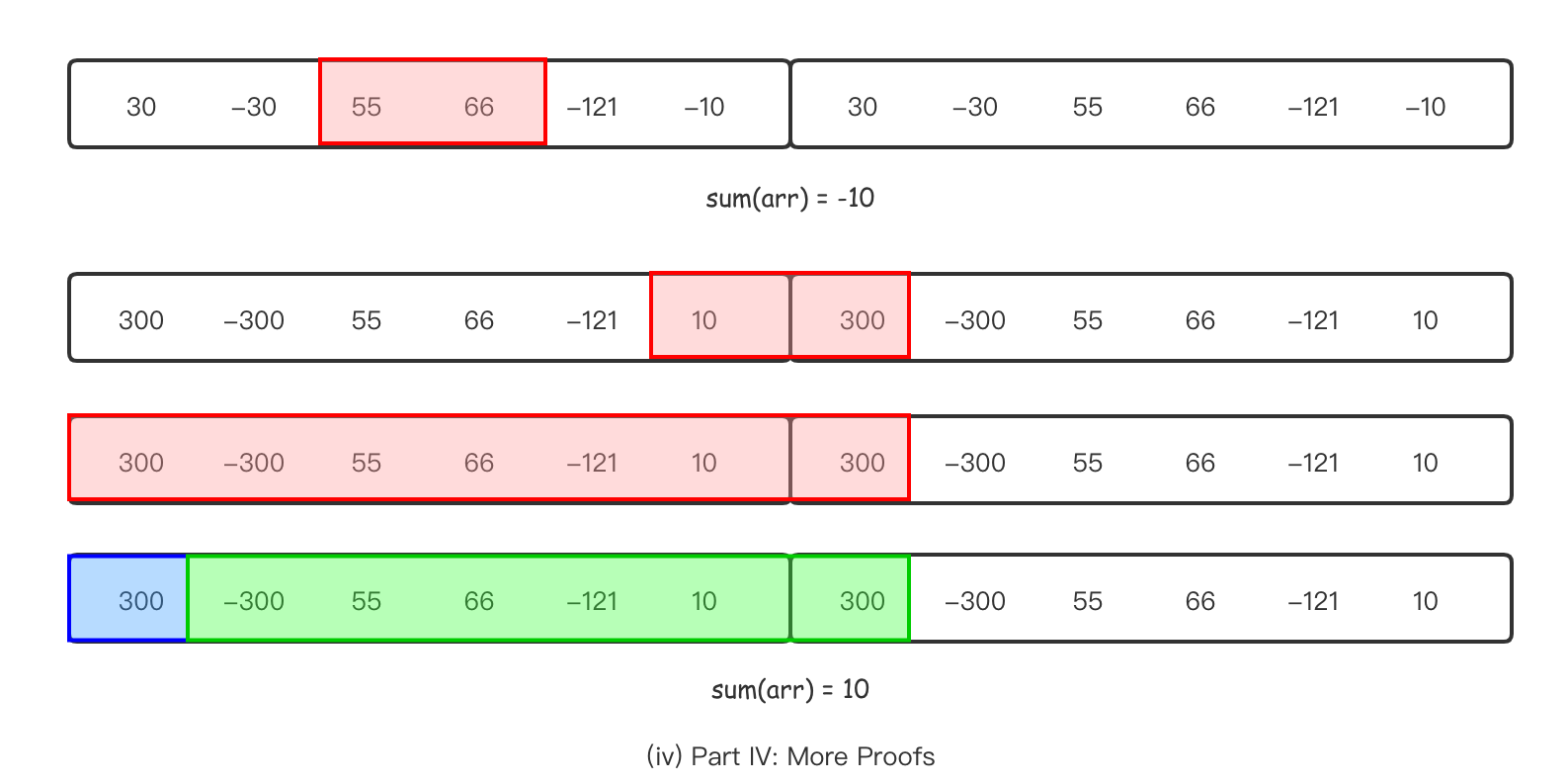
通俗来讲，就是最终的最大连续子数列和分为如下几种情况

• 常规型：formal(i, j)，不论 sum(arr) 大于0还是小于0，都与其一个单独数组的最大连续子数列和无关。
• 非常规型：nonformal(i, j)，这个时候有两种情况
  • sum(arr) <= 0 && j == arr.length - 1，此时可能 sum(arr[0], ..., arr[m], nonformal(i, j) > nonformal(i, j)
  • sum(arr) > 0，此时必有 sum(arr) + nonformal(i, j) > nonformal(i, j)