目录
04
自变量取值范围
函数连续，一阶导连续，判断邻域单调，邻域函数值
微积分物理应用
行列式 初等行变换，得基础解系，进而得通解
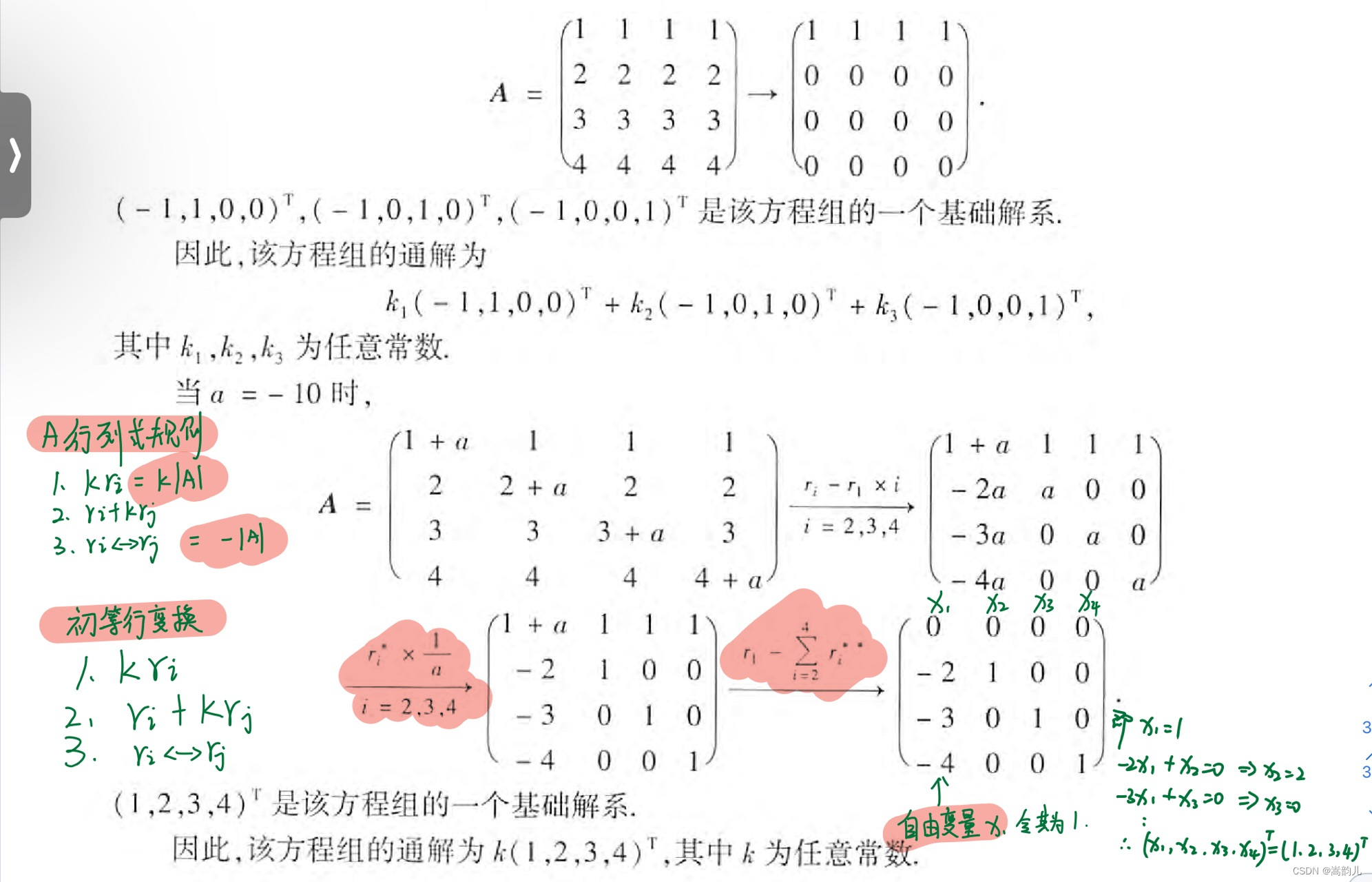
2005
讨论极限值，确定分段函数，不可导点
积分要素要明确，计算时合并同类项要注意看清楚
两种方法，求最值。第一，域内求驻点+边界点，合并消元，讨论函数单调性，范围内求边界值。第二用拉格朗日，通用一般法
二重积分，区域函数对称性要充分充分利用！简化计算
2006
向量组相关性
积分，两点，一、求导进行到底，二、+C
必须描述清楚，属于某个特征值的特征向量，k任意非零常数
逻辑严谨夹逼证明n个线性无关向量解
正交单位化，分两步，分别设向量用数学语言表示
2007
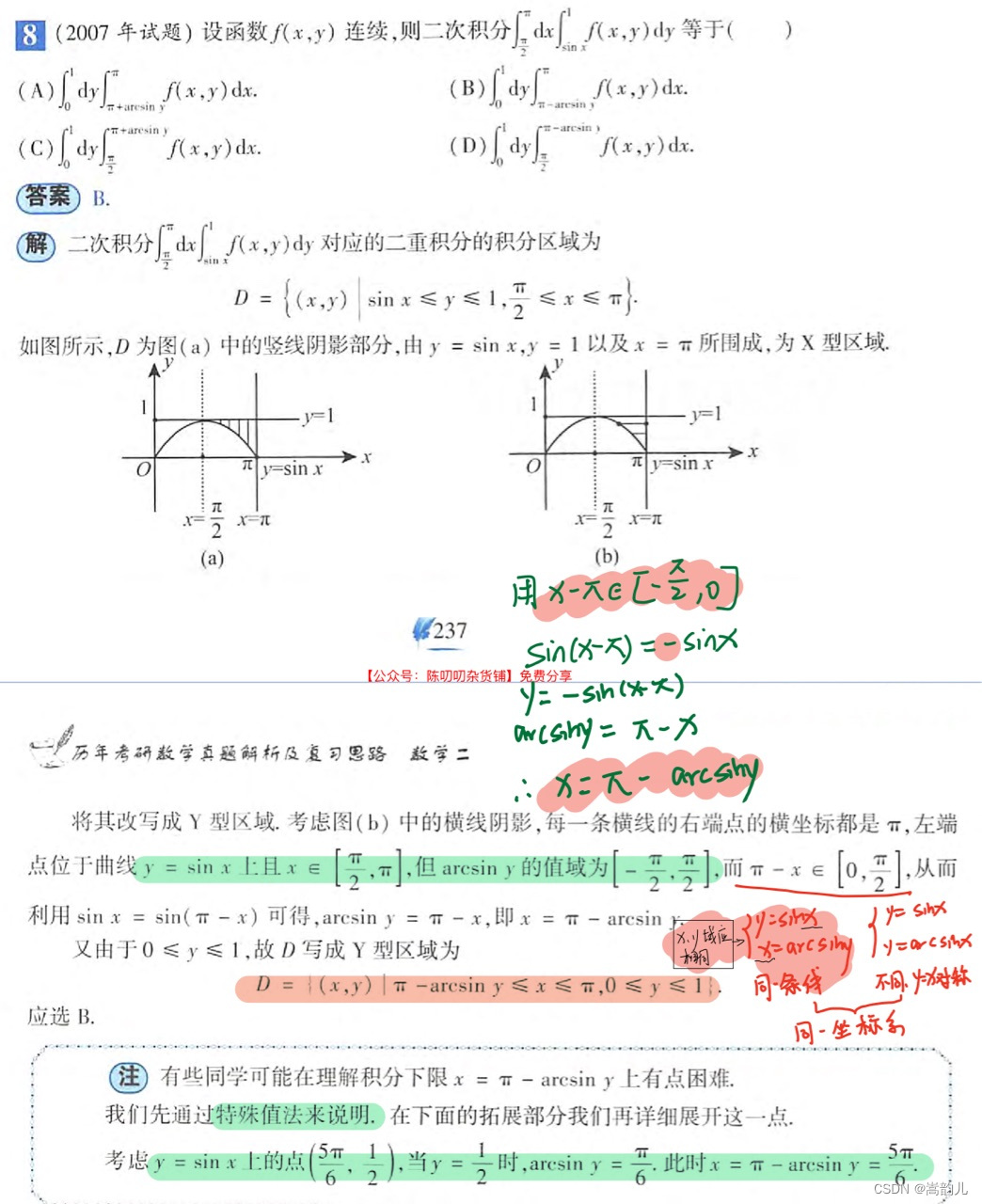
极限拆的原则，拆后都存在
二元函数，可微定义
取值范围问题，考虑清楚正负号±
找隐藏条件，实对称矩阵特征向量两两正交，得关系建立方程，夹逼定矩阵全部特征值特征向量
2008
外层函数单调有界，内层函数单调，则外层函数收敛，其余举反例，通常分段函数，常数，振荡函数
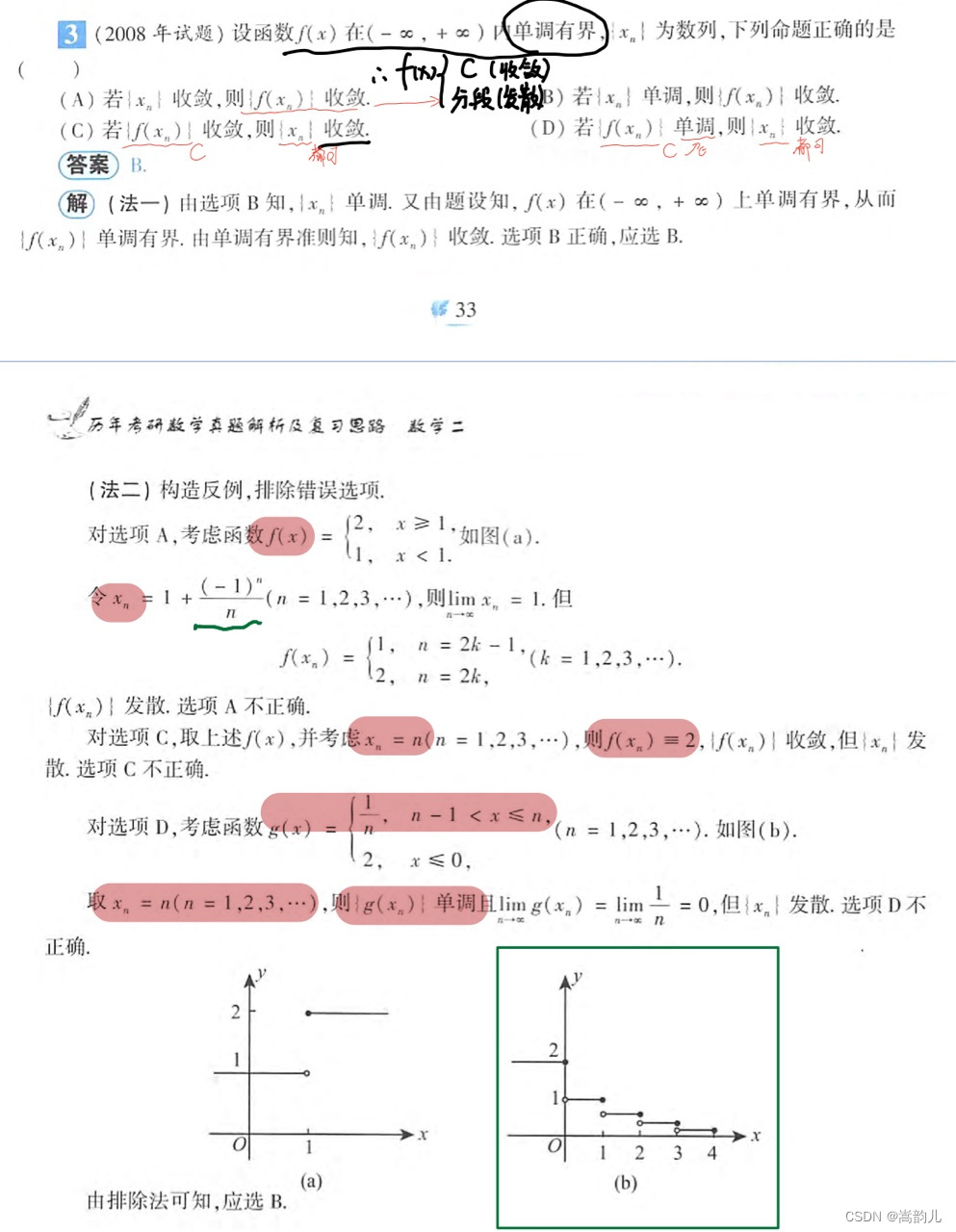
证明题两种思路， 已知条件都列出来，找关系建立方程。
反推法，若证明结论，需要满足什么条件。
行列式，递推求，逐行相减，数学归纳三种求值。克拉默法则求解x， 无穷解求基础解系+特解。注意特殊矩阵基础解系求法，
2009
间断点问题，分母趋于0，极限不一定是无穷，还得看分子是常数/0/∞。未定式求极限应该满足洛必达条件
极值点用充分条件判定，偏导数...ac-b²与0做比较。连续判定，因为有全微分形式，则函数必连续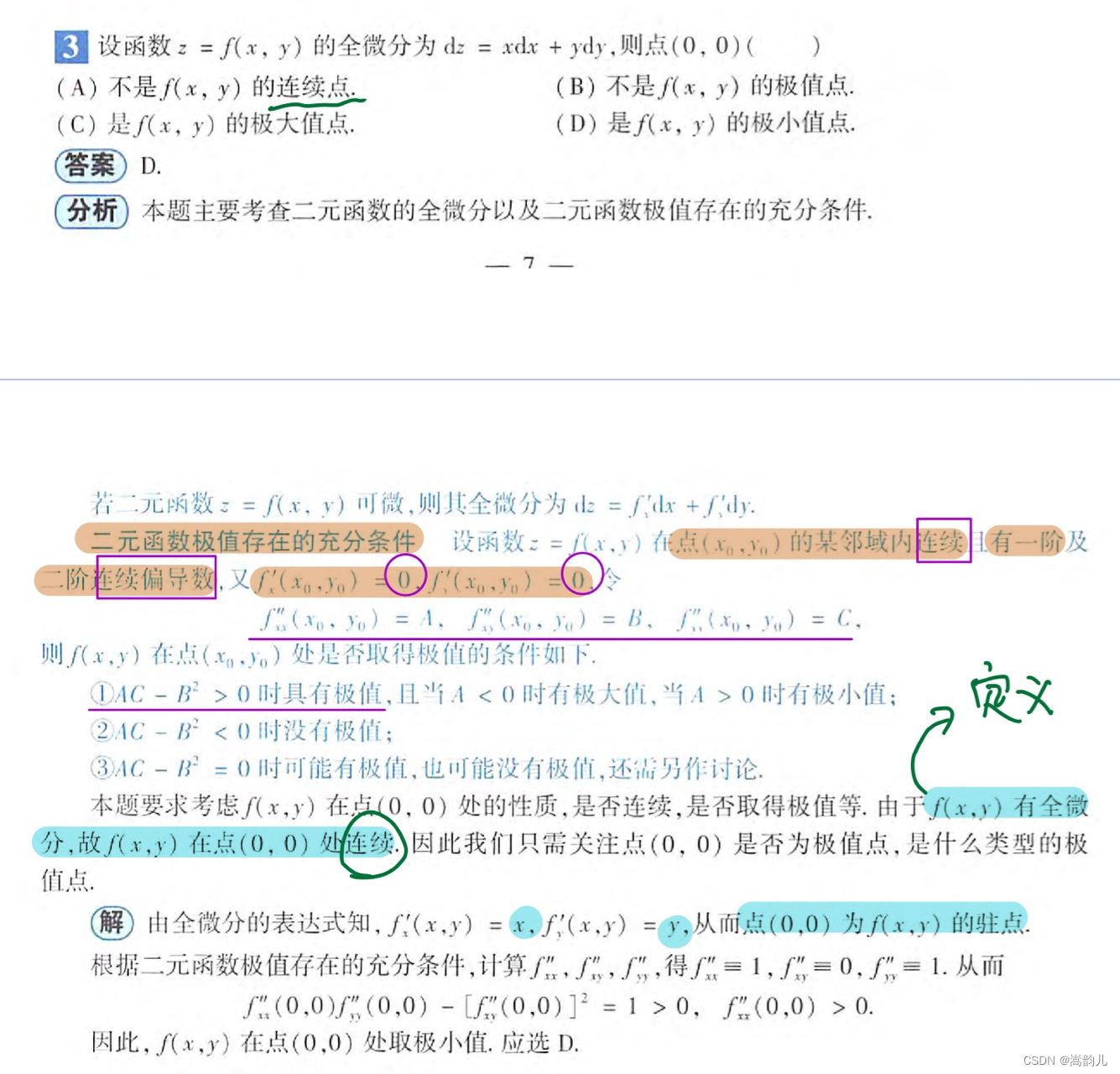
曲率圆方程→曲圆半径R→曲率K→二阶导与一阶导的关系式；曲率圆图 可近似 代替一段 原函数的图，此时二阶导±正负即可确定，一阶导单调性随之确定；一阶导与原函数 联想到 拉格朗日定理
零点存在定理，两端值异号，则区间内必存在零点。
极值判定，第一条件，一阶导是否变号。第二条件，一阶导＝0，二阶导大小。
迹的应用，
分段函数，求微分方程 。光滑曲线 暗含，函数连续，一阶导连续
拉格朗日证明，用罗尔→闭区间连续，开区间可导，端点值相等，则区间内必存在零点。难点在于凑型构建辅助函数
导函数定义证明邻域内有极限值
二次型系数
2010
微分方程的解
求极限，用积分定义，二重积分
多元 复合函数 偏导
说明偏导连续，二阶值（混合偏导）相等
两次 拉格朗日 ，划分区间
一般矩阵与实对称矩阵
2011
伴随矩阵，矩阵的解集与秩的关系
微分方程，三个变量，建立关系
基本不等式证明，构造辅助函数/单调性/积分不等式
数列是否收敛，考虑到用第一问结论,,,，证单调（相邻之差/之比），证有界 凑出第一问的形式，逐行累加
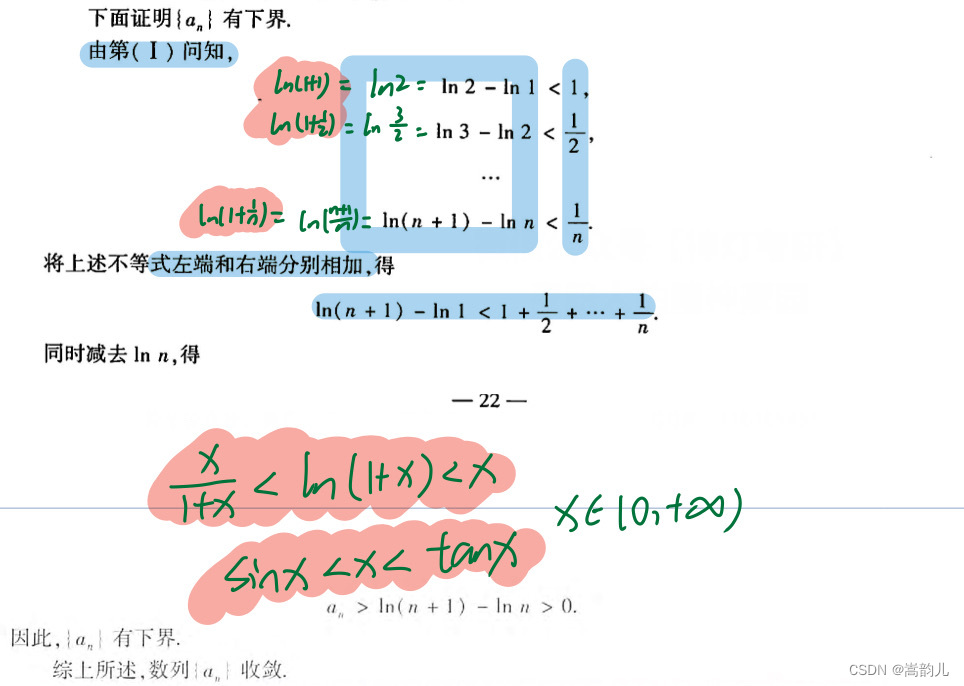
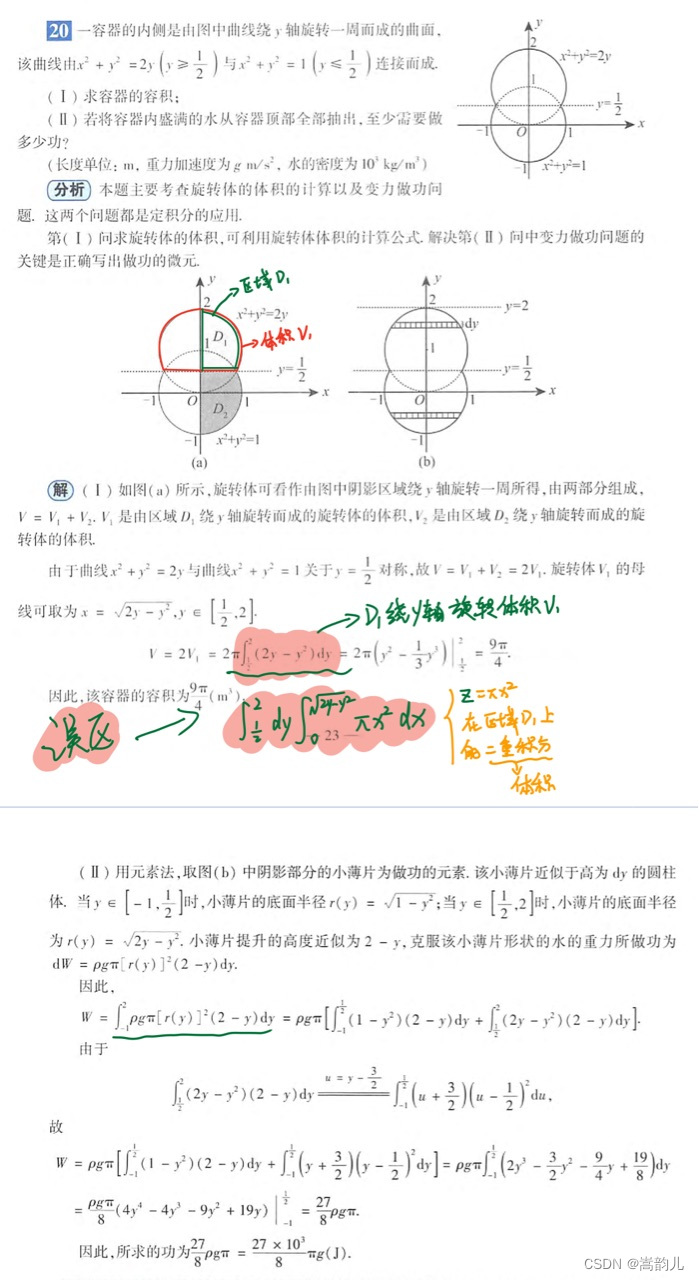
计算体积，二重积分与积分误区
2012
函数有界推数列收敛，有附加条件An=＞0
函数偏导的理解，图示法，函数计算法
证明题，区间对称，考虑函数对称，
对于放缩思想要敏感
单调性证明，泰勒公式证明
函数证明有且仅有一根，连续零点定理
数列极限，先证存在，单调有界，
第一问过于简单，则需要简单证明
正交变换的误区注意，正交单位化
变换的矩阵与标准型对应
2013
微分方程解的结构
伴随矩阵，转置，行列式关系
暴力求极限，泰勒
加项减项
证明题，拉格朗日，
构造辅助函数，凑出罗尔定理
辅助函数通法
拉格朗日数乘，条件极值，➕端点值
讨论值的范围，分析排除＝0的情况
形心坐标，计算二重积分，确定函数走向，再确定积分区域
一阶二阶导数，判定积分区间函数是否连续或者分段处理
同阶矩阵相乘，迹相等，具体描述看题
大胆假设未知，用已知条件解决
证明二次型，对应矩阵是对称矩阵 ，
正交单位向量，特点
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
