EMD基础学习---emd例子

e1.执行经验模式分解并可视化信号的希尔伯特频谱

加载并显示由频率变化明显的正弦波组成的非平稳连续信号。手提钻的振动和烟花的声音是非平稳连续信号的示例。信号以一定速率采样$fs$。

load('sinusoidalSignalExampleData.mat','X','fs')
t = (0:length(X)-1)/fs;
plot(t,X)
xlabel('Time(s)')

混合信号包含具有不同幅度和频率值的正弦波。

要创建希尔伯特频谱图，您需要信号的本征模式函数（IMF）。执行经验模式分解，以计算信号的IMF和残差。由于信号不平滑，因此将 'pchip' 指定为插值方法。

emd(X,'Interpolation','pchip','Display',1)

---

Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 2 | 0.026352 | SiftMaxRelativeTolerance
2 | 2 | 0.0039573 | SiftMaxRelativeTolerance
3 | 1 | 0.024838 | SiftMaxRelativeTolerance
4 | 2 | 0.05929 | SiftMaxRelativeTolerance
5 | 2 | 0.11317 | SiftMaxRelativeTolerance
6 | 2 | 0.12599 | SiftMaxRelativeTolerance
7 | 2 | 0.13802 | SiftMaxRelativeTolerance
8 | 3 | 0.15937 | SiftMaxRelativeTolerance

---

分解停止是因为残差信号的极值数小于’MaxNumExtrema’。

emd生成一个包含原始信号、前3个imf和残差的交互图。在命令窗口中生成的表指示每个生成的IMF的sift迭代次数、相对公差和sift停止标准。可以通过删除'Display'名称-值对或将其指定为0来隐藏表。

右键单击绘图中的空白处以打开IMF选择器窗口。使用IMF选择器有选择地查看生成的IMF、原始信号和残差。

从列表中选择要显示的IMF。选择是否在绘图上显示原始信号和残差。

选定的imf现在显示在绘图上。

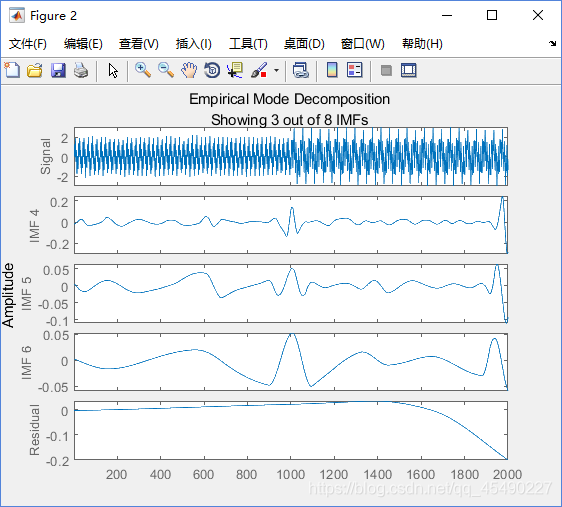
使用绘图来可视化从原始信号分解的各个分量以及残差。注意，残差是针对IMF的总数计算的，并且不会根据IMF选择器窗口中选择的IMF而改变。

利用经验模态分解得到的imf分量，创建Hilbert谱图。

[imf,residual,info] = emd(X,'Interpolation','pchip');
hht(imf,fs)

频率与时间的关系图是一个稀疏的关系图，带有一个垂直的色条，指示IMF中每个点的瞬时能量。该图表示从原始混合信号分解的每个分量的瞬时频谱。三个IMF出现在图中，频率在1秒时发生明显变化。

e2.正弦函数本征模函数的过零点与极值

这个三角恒等式表示同一物理信号的两种不同观点：
$$\frac{5}{2}cos2\pi f_{1}t+\frac{1}{4}(cos2\pi (f_1+f_2)t+cos2\pi (f_1-f_2)t)=(2+co{s}^2\pi f_{2}t)cos2\pi f_{1}t$$
生成两个正弦波，$s$ 和 $z$，使得 $s$ 是三个正弦波的总和，并且 $z$ 是具有调制幅度的单个正弦波。通过计算两者之差的无穷大范数，验证两个信号是否相等。

t = 0:1e-3:10;
omega1 = 2*pi*100;
omega2 = 2*pi*20;
s = 0.25*cos((omega1-omega2)*t) + 2.5*cos(omega1*t) + 0.25*cos((omega1+omega2)*t);
z = (2+cos(omega2/2*t).^2).*cos(omega1*t);

norm(s-z,Inf)

绘制正弦曲线并选择从2秒开始的1秒间隔。

plot(t,[s' z'])
xlim([2 3])
xlabel('Time (s)')
ylabel('Signal')

获得信号的频谱图。频谱图显示了三个不同的正弦分量。傅里叶分析认为这些信号是正弦波的叠加。

pspectrum(s,1000,'spectrogram','TimeResolution',4)

利用emd计算信号的固有模函数（imf）和附加的诊断信息。默认情况下，该函数输出一个表，该表指示每个IMF的筛选迭代次数、相对公差和筛选停止标准。经验模态分解将信号看作 $z$。

[imf,~,info] = emd(s);

过零次数和局部极值最多相差一。这满足了信号成为IMF的必要条件。

info.NumZerocrossing - info.NumExtrema

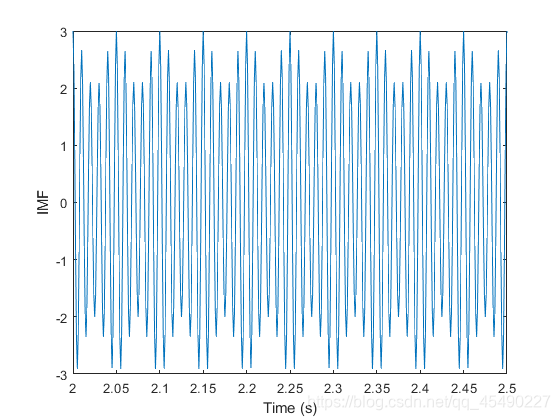
绘制IMF图，选择0.5秒的间隔，从2秒开始。IMF是调幅信号，因为emd将信号视为调幅信号。

plot(t,imf)
xlim([2 2.5])
xlabel('Time (s)')
ylabel('IMF')

e3.计算振动信号的固有模态函数

模拟损坏轴承的振动信号。执行经验模式分解以可视化信号的imf并查找缺陷。

中径为12厘米的轴承有八个滚动元件。每个滚动体的直径为2厘米。当内圈以每秒25个循环的速度驱动时，外圈保持静止。加速计在$10kHz$下对轴承振动进行采样。

fs = 10000;
f0 = 25;
n = 8;
d = 0.02;
p = 0.12;

健康轴承的振动信号包括几个阶的驱动频率。

t = 0:1/fs:10-1/fs;
yHealthy = [1 0.5 0.2 0.1 0.05]*sin(2*pi*f0*[1 2 3 4 5]'.*t)/5;

在测量过程的中途，轴承振动会产生共振。

yHealthy = (1+1./(1+linspace(-10,10,length(yHealthy)).^4)).*yHealthy;

共振导致轴承外圈出现缺陷，导致逐渐磨损。该缺陷导致一系列冲击，这些冲击在轴承的滚珠通过频率外圈（BPFO）处再次出现：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-506qB5u0-1596946713789)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\1596939073602.png)]

其中$f_0$为传动速率，$n$为滚动体数，$d$为滚动体直径，$p$为轴承中径，$\theta$为轴承接触角。假设接触角为15°，并计算BPFO。

ca = 15;
bpfo = n*f0/2*(1-d/p*cosd(ca));

使用pulstran函数将撞击建模为5毫秒正弦曲线的周期序列。每个3khz正弦波由一个平顶窗口加窗。利用幂律在轴承振动信号中引入渐进磨损。

fImpact = 3000;
tImpact = 0:1/fs:5e-3-1/fs;
wImpact = flattopwin(length(tImpact))'/10;
xImpact = sin(2*pi*fImpact*tImpact).*wImpact;

tx = 0:1/bpfo:t(end);
tx = [tx; 1.3.^tx-2];

nWear = 49000;
nSamples = 100000;
yImpact = pulstran(t,tx',xImpact,fs)/5;
yImpact = [zeros(1,nWear) yImpact(1,(nWear+1):nSamples)];

通过向健康信号添加影响来生成BPFO振动信号。绘制信号并选择0.3秒的间隔，从5.0秒开始。

yBPFO = yImpact + yHealthy;

xLimLeft = 5.0;
xLimRight = 5.3;
yMin = -0.6;
yMax = 0.6;

plot(t,yBPFO)

hold on
[limLeft,limRight] = meshgrid([xLimLeft xLimRight],[yMin yMax]);
plot(limLeft,limRight,'--')
hold off

放大选定的间隔以可视化影响的效果。

xlim([xLimLeft xLimRight])

在信号中加入高斯白噪声。指定“噪波方差”为$1/150^2$.

rn = 150;
yGood = yHealthy + randn(size(yHealthy))/rn;
yBad = yBPFO + randn(size(yHealthy))/rn;

plot(t,yGood,t,yBad)
xlim([xLimLeft xLimRight])
legend('Healthy','Damaged')

利用emd对健康轴承信号进行经验模态分解。计算前五个固有模函数（imf）。使用'Display'名称-值对显示一个表，其中包含筛选迭代次数、相对公差和每个IMF的筛选停止条件。

imfGood = emd(yGood,'MaxNumIMF',5,'Display',1);

Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 3 | 0.015551 | SiftMaxRelativeTolerance
2 | 3 | 0.078816 | SiftMaxRelativeTolerance
3 | 8 | 0.085954 | SiftMaxRelativeTolerance
4 | 1 | 0.0043681 | SiftMaxRelativeTolerance
5 | 2 | 0.010567 | SiftMaxRelativeTolerance
The decomposition stopped because ‘MaxNumIMF’ was reached.

使用没有输出参数的emd来可视化前三个IMF和residual。

emd(yGood,'MaxNumIMF',5)

计算并可视化缺陷方位信号的IMFs。第一个经验模式揭示了高频冲击。随着磨损的进行，这种高频模式的能量增加。第三个振型显示振动信号中的共振。

imfBad = emd(yBad,'MaxNumIMF',5,'Display',1);

Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 2 | 0.030781 | SiftMaxRelativeTolerance
2 | 3 | 0.095804 | SiftMaxRelativeTolerance
3 | 4 | 0.15371 | SiftMaxRelativeTolerance
4 | 1 | 0.014778 | SiftMaxRelativeTolerance
5 | 2 | 0.04312 | SiftMaxRelativeTolerance
The decomposition stopped because ‘MaxNumIMF’ was reached.

emd(yBad,'MaxNumIMF',5)

分析的下一步是计算提取的imf的Hilbert谱。